面向语言模型的全自动单元结构搜索

万 全，吴 霖，余正涛

(昆明理工大学 信息工程与自动化学院，昆明 650500)(昆明理工大学 云南省人工智能重点实验室，昆明 650500)

1 引 言

语言建模是自然语言处理领域的一项基本任务.从20世纪70年代的统计语言模型N-gram到现在广泛使用的神经网络语言模型，这些优秀的模型结构都是通过人工设计得到的.最近提出的神经网络结构搜索(NAS)引起了大量研究者的关注，NAS的目的是不在人工干预的情况下，让机器在给定的数据集上自动的搜索出性能优异的网络结构，从而将传统手工设计网络结构的过程变为自动.NAS的出现大大减少了研究人员在神经网络结构设计上所花的时间.Baker等人早期提出的基于强化学习的MetaQNN[1]方法，在一个庞大的搜索空间内实现了网络结构的自动搜索.接下来是进化算法[2，3]在NAS中的应用，通过对初始的简单网络结构进行操作的增加或改变来自动搜索性能优异的网络结构.这两类方法存在一个共同的问题，搜索过程中需要对所有采样到的网络结构性能进行评估，不仅需要花费大量的时间，同时还需要强大的硬件支持，实验过程基本无法复现.

现在最流行的NAS方法是Liu等人于2019年提出的可微神经网络结构搜索DARTS[4]，相对于较早的在离散空间进行结构搜索的强化学习[1，5-7]和进化算法[2，3]等方法，基于梯度优化的DARTS方法构造了一个连续的搜索空间，在搜索速度和实验硬件要求上都更有优势，普通研究人员更容易复现，因此成为了目前大多数NAS研究者的基础方法.DARTS方法在搜索空间的构造上和Pham等人提出的ENAS[7]方法类似.在语言模型任务上，网络结构的类型为循环神经网络(RNN)，DARTS的目的是搜索出组成循环神经网络单元(cell)的内部结构(如图1所示).单元内部定义为包含若干节点的有向无环图，在每两个节点之间放置所有可采取的操作并为所有操作随机分配权重，经过训练后利用softmax决策选择节点与节点之间最佳的操作得到优秀的网络结构.DARTS在NAS研究上取得了一定的成功，但搜索过程中包含了人工处理的过程，因此不能完全符合NAS不靠人工干预让机器自动设计网络结构的要求.

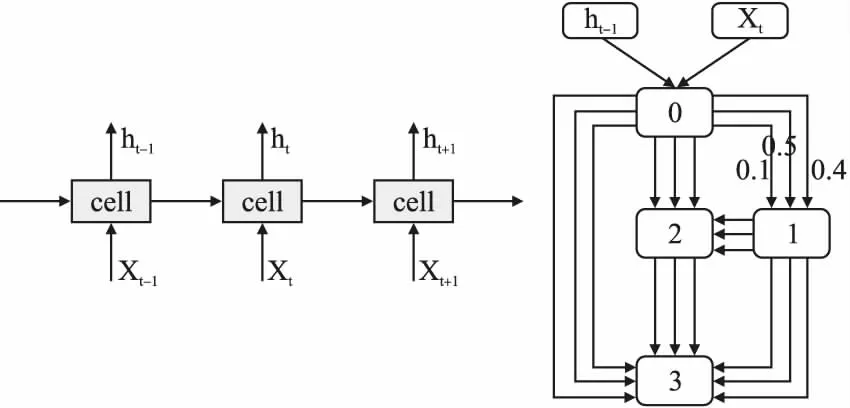
图1 DARTS方法定义的网络结构框架图(左)和单元内部结构图(右)

针对该问题，本文提出一种全自动单元搜索空间.首先，移除搜索阶段包含的人工处理过程实现单元搜索全自动化.然后，在单元内部额外增加元素相加(add)和元素相乘(elem_mult)操作，抵消移除人工处理过程后导致的模型规模变小和复杂度降低的问题.最后，DARTS限制softmax决策每次只选择权重最高的一个操作且softmax作用于每两个节点之间，而增加的add和elem_mult需要选择两个输入进行操作.因此，将前序所有节点每两个为一组作为输入，然后进行add和elem_mult操作，得到一个输出并作为后序节点的输入，同时改变softmax决策为对单个节点的所有输入统一进行softmax.

本文在语言模型任务上对提出的方法进行了验证，数据集选用的是目前训练语言模型时使用最广泛的Penn Treebank(PTB)数据集.本文通过设定不同的节点数量，以及不同组合的操作，探讨与语言模型任务最匹配的搜索空间.实验表明，在节点数量为11，移除人工处理并同时增加add和elem_mult操作时表现最好，搜索到的网络结构在PTB测试集上取得了56.2的测试困惑度.为了验证本文方法搜索到的结构的可迁移性，将PTB数据集上搜索到的最优结构迁移到Wikitext-2(WT2)数据集进行训练，在测试集取得了70.1的测试困惑度.

2 相关工作

神经网络结构搜索作为一种新的自动机器学习技术已经被应用于计算机视觉和自然语言处理领域.初期的方法都是基于强化学习[1，5-7]对问题建模，随后进化算法[2，3]也在结构搜索研究中取得了重大进展，最近，基于梯度优化方法的DARTS[4]成功应用于图像识别和语言建模任务上，对比强化学习和进化算法，基于梯度的方法有着更低的硬件要求和更高的搜索效率，这也使之成为了目前广泛使用的结构搜索方法.

DARTS尽管有着优秀的性能，但大多数人验证了其性能崩溃的问题，并指出其崩溃的原因是因为过多的skip connection.为了解决该问题，Chen等人提出PDARTS[9]对搜索空间进行了限制，通过设置dropout rate对skip connection进行裁剪，并人为限制skip connection的数量.Zela等人[10]设计多个搜索空间，并证明了skip connection是导致DARTS崩溃的主要原因，为了增强搜索过程的稳定性，他们提出对模型的验证损失进行监督，但这增加了额外的计算量.Chu等人[11]提出放宽搜索空间，避免排他性竞争，通过使用sigmoid函数模仿编码从而使每个操作具有独立的体系结构权重.Zhang等人[12]则是通过在训练过程中加入无偏且方差较小的噪声来解决skip conncetion问题.这些改进的DARTS方法在计算机视觉领域取得了较大的成功，甚至在个别任务上达到了state-of-the-art的结果.

与计算机视觉领域不同，结构搜索在自然语言处理领域的研究相对较少，Transformer模型[13]依然处于王者地位.由于自然语言处理领域的模型往往更加复杂，规模也更大，已有的结构搜索方法不足以从零开始设计出如此复杂且庞大的网络结构，在机器翻译这类顶层任务上，都是以一个种子模型为基础展开搜索优化，在语言模型等底层任务上则可以进行完整的搜索.Le等人将进化算法用于机器翻译任务，他们首次将结构搜索用于前馈模型，以Transformer为种子网络，成功搜索出了表现更好的Evolved Transformer网络[14].Wang等人提出了坐标式结构搜索方法[15]，在Transformer的基础上，通过增加LSTM或其他层达到了优于原模型的效果.微软团队在2019年国际机器翻译大赛[16]上，将自己提出的基于梯度优化NAO[17]方法用于Transformer模型，它将模型结构编码并嵌入到一个连续的向量空间，然后通过梯度优化发现并解码出性能更好的结构.

3 方 法

3.1节对比了全自动的单元框架和DARTS原始单元框架，本文方法通过移除单元搜索过程中包含的人工处理过程，实现单元搜索过程全自动化，其目的是为了更加符合结构搜索无需人工干预，让机器自动设计网络的要求.人工处理过程主要是对两个输入进行一些固定的操作得到一个输出，然后将这个输出作为搜索单元的输入.移除人工处理过程后会有两个影响，一是导致网络规模的减小，二是导致网络复杂度下降，针对这两个问题，在3.2节中通过增加节点数量并引入add和elem_mult操作来抵消移除人工处理过程带来的影响.由于额外增加的操作每次需要两个输入，且两个输入为任意两个前序节点的输出，而DARTS限制softmax每次只选择一个权重最大的操作，且softmax的作用域为每两个节点之间，这样的限制会与额外增加的操作产生冲突，因此在3.3节中对softmax决策进行了修改，取消了算法的限制.

3.1 全自动单元搜索框架

在进行结构搜索之前，需要先定义一个合理的搜索空间，从而最大化结构搜索的性能，得到优秀的网络结构.在DARTS中，其定义了一个半自动的搜索单元，如图2上所示，输入为序列当前时刻的输入x_t和上一时刻的隐状态h_(t-1)，经过特定的人工处理将两个输入合并为一个作为单元的输入，然后进行单元结构的搜索过程，整个流程为：输入-人工处理-结构搜索-输出.这样的处理方式显然并不满足结构搜索自动化的要求.因此本文提出了全自动化的单元搜索框架，如图2下所示，通过移除原始搜索框架中的特定人工处理过程，从而实现全自动化的单元结构搜索.输入方面与半自动框架一样，都是序列当前时刻的输入x_t和上一时刻的隐状态h_(t-1)，但是不再对输入进行人工处理，而是直接传入搜索单元进行结构搜索，最后得到输出，整个流程为：输入-结构搜索-输出.

图2 DARTS定义的半自动单元搜索框架(上)和本文方法定义的全自动单元搜索框架(下)

3.2 节点和操作的增加

将上一节DARTS人工处理过程的网络结构拓扑图可视化表示，如图3左所示，图3右为DARTS搜索到的单元结构拓扑图.通过对比发现，人工处理过程的网络结构复杂度明显高于搜索到的单元结构的复杂度.因此，当移除人工处理过程后，一方面会使网络结构趋于简单化，另一方面，网络规模也会减小.为了抵消移除人工处理过程带来的影响，本文增加了单元内节点的数量并引入add和elem_mult操作(add操作表示将两个单元的输出相加，elem_mult操作表示将两个节点的输出相乘).单元内每个节点代表一层网络，增加节点数量就是增加网络的层数，从而避免网络规模的减小.相比tanh等激活函数，add和elem_mult操作最大的不同在于每个操作需要两个输入，这样就能使得保持网络结构保持一定的复杂度.

图3 DARTS人工处理过程网络结构拓扑图(左)和搜索到的单元网络结构拓扑图(右)

3.3 Softmax决策

在3.2节中，add和elem_mult操作被引入用来维持网络结构的规模和复杂度，但是DARTS算法中的softmax会与这两种操作产生冲突.DARTS定义softmax决策在每两个节点之间进行，如图4左所示，节点3会分别对节点1和节点2的所有输出进行softmax，而add和elem_mult这两种操作每次都需要选择两个节点，因此本文修改了softmax决策的使用，将每两个节点之间的局部softmax扩展为单个节点的全局softmax，如图4右所示，首先将1节点和2节点进行add或elem_mult操作，然后与节点的其他操作一起进行softmax再传入3号节点，这样就消除了softmax的局限性.

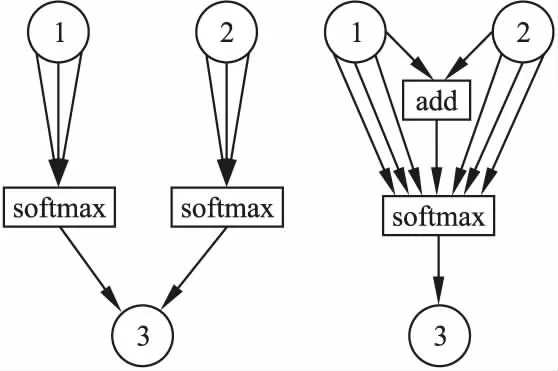
图4 DARTS算法的softmax决策(左)和本文方法的softmax决策(右)

3.4 搜索空间

在移除人工处理过程、增加操作种类和节点数量以及修改softmax决策后，就可以对搜索空间进行完整的定义.网络结构的搜索类型依然是以单原为基础，通过搜索优秀的循环神经单元以构成循环神经语言模型.单元的输入为当前序列的输入 x_t和上一时刻的隐状态h_t-1，输出为所有没有输出的中间节点的和取平均值.单元内节点的数量由8个增加到11个以保持网络规模大小，节点间可采取的操作由4个增加至6个，分别是tanh，relu，sigmoid，identity，add和elem_mult.

3.5 搜索算法

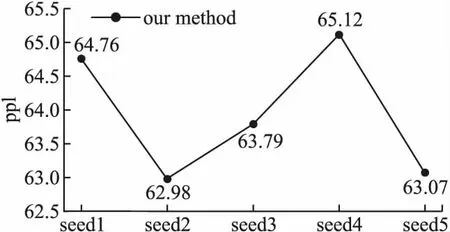
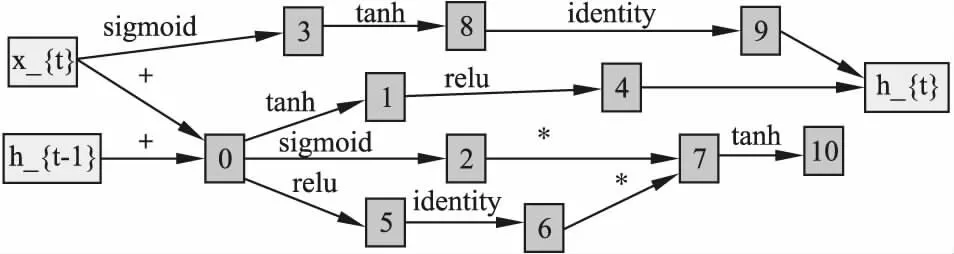
搜索算法方面采用DARTS方法作为指导策略.因为强化学习和进化算法都需要足够大的GPU群才能进行搜索，而DARTS在硬件方面的要求比前两种方法要低得多，搜索速度上也更加高效，所以DARTS方法成为了首要选择.Darts方法的搜索流程主要有4步：1)构造一个包含若干接点的有向无环图，大号节点的输入为所有小号节点的输出加权取平均值；2)在每两个节点之间放置所有可以采取的操作，从而将离散的网络结构变得连续；3)结构权重α与网络权重w的联合优化过程，找到最大的权重α所对应的操作；4)根据学习到的结构权重α固定网络结构，初始化所有网络权重w，进行最后的训练.设一组有序节点node(1)，node(1)，…，node(n),o(i,j)(i

nodej=∑i

(1)

(2)

4 实验与分析

本文的主实验为单元结构的搜索实验，在PTB数据集上进行，方法性能在语言模型任务上进行评估.搜索实验包含搜索阶段和评估阶段，搜索阶段通过多次实验选择在验证集上困惑度最低的结构为待选结构，评估阶段对搜索阶段得到的待选结构结构在训练集上重新训练，经过一段时间后选择验证集最低的结构为最优结构，最后进行模型的完整训练，并在测试集评估其性能.接下来在WT2数据集上对本文方法搜索到的模型结构的可迁移性进行验证.最后进行消融实验分析模型的性能与规模和复杂度之间的关系.

4.1 搜索阶段

由于结构搜索技术对结构的初始化比较敏感，因此在PTB数据集上对搜索阶段重复5次，以降低其敏感度.模型结构为单层循环神经网络，词嵌入层和隐藏层均包含300个神经元，batch_size大小设为256.循环单元的输入有两个，分别为序列当前时刻的输入x_t和上一时刻的隐藏状态h_(t-1).搜索单元的输出没有延续DARTS中的设置，而是和ENAS中的输出设定一样，为中间所有没有输出节点的值相加然后取平均值.搜索单元内部设置了11个节点，节点之间可采取的操作包含tanh，relu，sigmoid这3种激活函数，identity线性变换，以及add和elem_mult两种基本操作.优化阶段首先使用随机梯度下降(SGD)算法对网络权重w进行优化，学习率大小为20，权重衰减为5e-7，然后使用Adam算法对结构权重α进行优化，初始学习率大小设置为3e-3，权重衰减为1e-3.以不同的初始结构分别进行50个epoch的搜索，得到5个待选结构.

4.2 评估阶段

评估阶段对搜索阶段得到的5个待选结构进行短暂评估，选出最优结构.模型的词嵌入层和隐藏层包含的神经元数量由搜索阶段的300个增加到850个，batch_size大小为64，权重w的优化方法使用平均随机梯度下降(ASGD)算法，初始学习率为大小为20，权重衰减大小为8e-7.将5个待选单元结构的网络权重w随机初始化，然后在训练集上训练300个epoch，此时在验证集上困惑度最低的单元结构就是最优结构，图5显示了5个待选结构分别训练300个epoch时的困惑度大小，最低的困惑度为62.98，最优单元结构如图6所示.接下来，选择最优单元结构构成循环神经网络，再次初始化模型权重w，在训练集上充分训练直到其收敛，结果如表1所示.

图5 5个待选结构在PTB数据集上训练300个epoch时验证集上的困惑度

图6 本文方法搜索到的最优单元结构拓扑图

表1 PTB数据集实验数据表

4.3 结构迁移

将4.2节中得到的最优单元结构直接迁移到WT2数据集验证模型结构的可迁移性.嵌入层和隐藏层的神经元数量均设置为700，权重衰减为5e-7.进行充分训练直到收敛，并在测试集上进行评估.表2为迁移到WT2数据集上的结果.

表2 PTB数据集实验数据表

4.4 消融实验

为了探讨节点数量和增加操作对网络结构性能的影响，本文做了如下消融实验：1)移除所有人工处理过程后进行实验，评估最低复杂度和最小规模下的网络结构性能；2)增加add和elem_mult操作，在节点数量为8和11时分别进行实验，研究网络规模对结构性能的影响；3)固定节点数量为11个，在不增加add和elem_mult操作、仅增加add操作、仅增加elem_mult操作和同时增加两种操作4种情况下进行实验，探索网络复杂度对结构性能的影响.所有的实验仅在PTB数据集上进行，实验结果如表3所示.

表3 消融实验数据表

4.5 结果分析

本文共进行了4个实验.首先，在搜索阶段，结构搜索对初始化结构的敏感，因此对搜索阶段的实验进行了5次，得到待选结构，然后通过训练集上的重新训练，得到最优的单元结构.接下来，在PTB数据集上验证本文提出的全自动单元结构搜索方法的有效性，实验在测试集上取得了56.2的困惑度，与基线方法相比还是相差了0.5个点.这种情况主要是由于增加节点数量和操作种类不足以抵消移除人工处理过程这一操作对网络规模和复杂度的影响.通过对3.2节中人工处理过程拓扑图的分析可以发现，这一过程包含的网络层数不止3层，但是由于实验GPU内存的限制，最多只能在单元内部额外增加3个节点，也就是只增加了3层网络，因此在网络规模上与基线模型还是存在差距，如果能在更大内存的GPU上，增加更多的节点数量，搜索到性能更好的网络结构的概率会更大.尽管如此，本文方法在实现单元搜索过程全自动的情况下，依然发现了比较有竞争力的结构，证明了该方法的可行性.然后，在WT2数据集上进行结构迁移性实验，与已有的结构搜索方法相比，70.1的测试困惑度处于同一水平，证明了本文提出方法的可迁移性.与手工设计的网络存在差距主要是因为手工网络是直接在WT2数据集上进行设计，而本文模型是从PTB数据集迁移得到的，模型结构与任务的匹配度存在差距，但是大大节约了设计成本，且达到了一个比较有竞争力的结果.最后，通过消融实验研究网络规模和网络复杂度对模型结构性能的影响.从表3可以发现，当移除所有人工处理过程，不增加节点数量，不增加可采取操作，此时网络复杂度和规模均处于最初始状态，这样的网络结构仅取得了62.3的测试困惑度.同时增加add和elem_mult操作使网络保持一定的复杂度，这种情况下，模型性能提升明显，取得了56.9的测试困惑度.扩大网络规模，增加单元内节点数量至11个，在增加单个操作时，网络性能差距不大.通过对比实验可以发现，无论是是网络结构的复杂度还是网络结构的规模对模型性能都有着较大的影响，因此，在实现单元搜索过程全自动的情况下，必须同时保持一定的网络规模和复杂度，才能搜索到性能优异的模型结构

5 总 结

本文提出了全自动单元结构搜索方法，并在语言模型任务上进行了验证.该方法了实现结构搜索过程的全自动化，并在PTB数据集上取得了56.2的测试困惑度.为了验证提出方法搜索到的结构的可迁移性，将PTB数据集上搜索到的最优结构迁移到WT2数据集进行训练，在测试集取得了70.1的困惑度.最后，为了研究模型与复杂度和规模之间的关系，本文对比了不同数量节点与操作之间的组合，实验表明，移除人工处理，增加节点并同时增加add和elem_mult操作时搜索到的网络结性能最优，说明模型结构需要保持一定的规模和复杂度才能搜索到性能优异的网络结构.