An Enhanced Searching Strategy for Multi-Agent Mobile Applications

Xiaoyu Zhang,Wei Liu,Fangchun Yang

1 School of Computer Science(National Pilot Software Engineering School),Beijing University of Posts and Telecommunications,Beijing 100876,China

2 State Key Laboratory of Networking and Switching Technology(Beijing University of Posts and Telecommunications),Beijing 100876,China

Abstract: Multi-agent mobile applications play an essential role in mobile applications and have attracted more and more researchers’attention.Previous work has always focused on multi-agent applications with perfect information.Researchers are usually based on human-designed rules to provide decision-making searching services.However,existing methods for solving perfect-information mobile applications cannot be directly applied to imperfect-information mobile applications.Here,we take the Contact Bridge,a multi-agent application with imperfect information,for the case study.We propose an enhanced searching strategy to deal with multi-agent applications with imperfect information.We design a self-training bidding system model and apply a Recurrent Neural Network(RNN)to model the bidding process.The bridge system model consists of two parts,a bidding prediction system based on imitation learning to get a contract quickly and a visualization system for hands understanding to realize regular communication between players.Then,to dynamically analyze the impact of other players’unknown hands on our final reward,we design a Monte Carlo sampling algorithm based on the bidding system model (BSM) to deal with imperfect information.At the same time,a double-dummy analysis model is designed to efficiently evaluate the results of sampling.Experimental results indicate that our searching strategy outperforms the top rule-based mobile applications.

Keywords: multi-agent mobile applications; imperfect information; deep neural network; Monte Carlo;Contact Bridge

I.INTRODUCTION

Multi-agent mobile applications have revolutionized how we live,work and interact with the world.Recently,computational games on mobile applications have always been important research.Researchers of computational games have been developing AI programs that can beat expert players.The research can be categorized in the following two directions.One is the study of multi-agent mobile applications with perfect information,such as chess[1],Go[1–3].The traditional method of solving such problems is to determine the decision by artificially defining rules.With the rapid development of deep learning,AI programs can make high-quality decisions more efficiently in perfect information games,making it possible to defeat expert players [4].For example,DeepMind has proposed an AlphaGo Zero algorithm,which taught itself three different board games in three days,including chess,Go,and Shogi,without human intervention.This algorithm updates the neural network through self-play to trounce all expert players.Another study aims at multi-agent mobile applications with imperfect information,such as Texas Hold’em[5,6],DeltaDou,Bridge,etc.In these applications,the main challenge is that information asymmetry makes constructing a single collective search tree problematic[7,8].Deep-Stack [5]and Libratus [6]achieve super-human level in Heads-Up No-Limit Texas Hold’em using Counterfactual Regret Minimization (CFR).CFR relies on a complete traversal of the game tree,and the traversal would be difficult for some games with large state space.

This paper uses the Bridge as a study case for multiagent mobile applications with imperfect information.We proposed an enhanced searching strategy including three techniques.

The first technique is a competitive bidding system model based on deep neural networks.In Bridge,the rules of the bidding system are very complicated,and it is impossible to obtain desired results by traditional artificial searching directly.Thus,we design two neural networks to deal with this problem.One is a bidding prediction network to choose a few bids initially,and the other is a visualization network for hand understanding to realize players’communication.

The second technique is a Monte Carlo sampling algorithm.In Bridge,each player has 13 cards; therefore,there would have been=8,122,425,444 possible states.In order to alleviate the problem of state explosion,we sampled data for each state obtained by the prediction network to construct a game tree of information set nodes.We add a hand understanding system that can predict the other players’hand distribution to transform imperfect information into perfect information as much as possible.

The third technique is a double-dummy analysis model with a neural network,which can quickly estimate a player’s score at high speed as a reward.In previous studies,the results of double-dummy analysis are obtained by calling the open-source library python-dds,which is not conducive to processing lots of deals obtained by Monte Carlo sampling.Therefore,we train a neural network model to analyze the double dummy results,which can efficiently process a large amount of sampled information.

The above three techniques are integrated into a framework to form an enhanced searching strategy.The searching strategy combines deep learning and Monte Carlo searching for studying bidding with the competition.That can not only learn the human bidding system to transmit information through data without manual input rules[9,10],but also pass information through Monte Carlo searching to make the decision.The main contributions of our work can be summarized as follows:

• Our searching strategy is suitable for multi-agent applications with imperfect information and large state space.

• We have realized the cooperation and game within the multi-agent applications with imperfect information.

• We conduct extensive experiments on the realworld data set and demonstrate the evident superiority.

The rest of this paper is structured as follows.Section II is related works.Section III provides the background of the Bridge.Section IV introduces the model framework with the algorithms for each phase in detail.Then we discuss experimental setups and present the results with evaluation in Section V.Finally,we conclude our work in Section VI.

II.RELATED WORKS

The Bridge consists of two phases,bidding and playing.There are pieces of software emerging,such as Bridge Baron,GIB,Snyrey [9]and Wbridge1,which are proven to be especially effective during the playing phase.However,bidding shows a more complex situation.Therefore,we only focus on Bridge bidding in this paper.

One of the first bridge bidding programs is written as early as 1970 [11].Wassermann [11]introduced bidding patterns.In addition to the opening and responding patterns,this program could distinguish several specific bids,such as double.Nevertheless,this program needs to transfer bridge experts’bidding techniques,commonly referred to as human bidding systems,to program code,which is finite.However,the rules of Bridge are extremely complex,which causes the inevitable ambiguity of the bids.To reduce this ambiguity,some works are conducted by considering human bidding systems.For example,GIB[12]strengthens the lookahead searching in bidding by borrowing rules from human bidding systems.Moreover,Amit et al.[13]attempted to use Monte-Carlo sampling combined with partition searching to reduce the size of the game tree.

All of the above work is based on the human bidding system.Nevertheless,Ho and Lin [14]proposed a new method adopting a contextual bandit algorithm to build decision trees to predict bids without considering human bidding systems.However,their model is limited to bidding from up to 5 options since the decision tree has only five simple nodes.Yeh and Lin[15]first tried using deep reinforcement learning to bid without depending on any human expert knowledge.They achieved some promising results,but their successes rely on simplifying models to the subproblem of bidding without competition which assumes that the opponent’s team always calls PASS during the bidding.This situation is scarce in real bridge games,making their model less functional.In contrast,DeLooze and Downey[16]focused on the problem of bidding with the competition.They used raw data as input for a special form of a neural network called a self-organizing map(SOM).Unfortunately,this approach is only used to bid no trump hands rather than any bids.However,Rong et al.considered the problem of the bid with the competition[17].We adopt some ideas from[16].We generate many examples from the Synrey platform and then use these as the input of our model.We also extend some ideas from[18].For example,We add a hand understanding system to help complete the automatic bidding strategy.

III.BACKGROUND

3.1 Imperfect Information Games

Many current pieces of research are based on perfect information games,such as chess and Go.In recent years,with the development of deep learning,the study of perfect information games has made rapid progress.AI players defeated world-class human players,an essential milestone in the history of artificial intelligence development.In October 2015,AlphaGo won the European Go Champion Fan Wei in 5:0,a professional two dan player.In March 2016,he challenged the World Go Champion Li Shishi,a professional nine dan player,to succeed.In October 2017,after making a massive breakthrough in Go,Deep-Mind explored other perfect information games,including Atari,chess,and Shogi.The paper showed that AlphaGo Zero taught itself three board games in three days.This result shocked the chess world,and AlphaGo Zero became the best chess player in the world.

However,the above are some researches on perfect information games.There are still many challenges in games with imperfect information due to their partial observability.One of the games that have attracted considerable attention is poker,and most previous work on poker has been limited to Texas Hold’em.The Computer Poker Research Group at the University of Alberta is a typical representative that pays more attention to Texas Hold’em Poker [19].They have solved heads-up Limit Texas Hold’em in 2015[20]and heads-up No-Limit Texas Hold’em in 2017[5].These systems treat poker as imperfect information games and find specific searching strategies for Texas Hold’em to get the game equilibrium.One of the standard approaches to computing strategies in such large games is to first generate many abstractions by combining similar game states,which is a smaller version of the game that retains as much as possible the strategic characteristics of the original game[21,22].Although DeepStack [5]and Libratus [6]have made significant progress in heads-up No-Limit Texas Hold’em,multi-player No-Limit Texas is still a technical problem due to the vast size of the space of hidden information.In Bridge,each player has 13 cards; therefore,there would have been=8,122,425,444 possible states,which is impossible to get the complete information.This is why most previous works on poker are limited to two-player Texas Hold’em.As for this problem,we decide to add a hand understanding system that can predict the other players’hand distribution to transform imperfect information into perfect information as much as possible.

3.2 Bridge Bidding

Bridge is a trick-taking card game played by four players using a standard 52-card deck.Four players(North,South,East,and West)are organized into two opposing teams,the North and South against the East and West.During the bidding phase,since only the in-hand cards are available to each player,each partnership needs to use an established bidding system to communicate information about their hand and obstruct the exchange of information from the competition team.Each partnership will explain the meanings of their actions during the bidding to the opponent when the request is issued.Each bid from the legitimated sequence of 1♣,1♢,1,1♠,1NT,2♣,...,7NT with three flexible bids of DOUBLE,REDOUBLE and PASS suggests a particular trump suit (or there is not a trump suit at all).The dealer initiates the bidding process,which ends if three sequential PASS calls follow a legitimate bid.The last non-PASS bid is to be the contract of Bridge.The player who bids the last non-PASS bid (referred to as the contract of Bridge)is called the declarer.The contract affects the score the declarer’s team can get in the playing phase,consisting of a number and a suit or no-trump.If the declarer’s team achieves the contract,it gets a positive score,and the opposing team receives an equal but negative score.

3.3 Bridge Bidding System

In the process of bridge bidding,players need to know the hands of their counterparts but cannot communicate directly.To make it easier for partners to communicate and understand each other’s hands,we can transmit information through a specific bidding system.The bridge bidding system is a set of artificially defined bidding rules that could express the hand characteristics.After a bid,players can guess more information about the hands held by other players according to the rules defined by the bidding system,which should include the number of cards of each suit and the High Card Points (HCPs)2.There are many bidding systems worldwide,and different bidding systems contain different rules.For example,the same bid may have different meanings in different systems.In bridge games,two teams can use different bidding systems,but when one party does not understand the meaning of the other party’s bid,the other party is obliged to explain the meaning conveyed by his bid.Therefore,in the bridge game,the enemy and the friend will get the same amount of information,so the players have to cooperate,and game based on the known information and finally get a high score to win the game.

There are many different bidding systems in the world.The bidding system is divided into natural and non-natural bidding systems.A well-known natural bidding system is Two Over One (2/1),used by amateur and professional players.A rule-compliant bidding system is a key to communication between players,so we used the real bidding data provided only by the Snyrey platform without manual rules input to learn a natural bidding system.This model can learn,store and deliver the specific information expressed by its bidding in real-time.It allows for real cooperation and communication with human players in the future.Table 1 is a few examples of different rules in the natural bidding system.

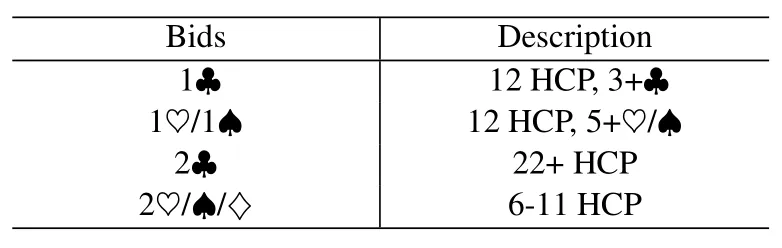
Table 1.Examples of natural bidding system rules.

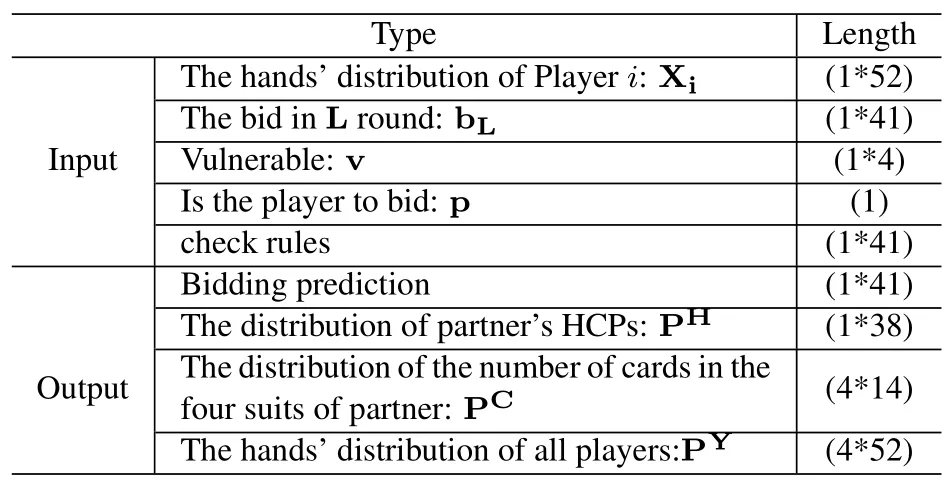
Table 2.Parameters for BSM.

IV.FRAMEWORK

This section provides the details of our proposed framework,shown in Figure 1.The framework includes four phases: the bidding system model,sampling algorithm,double-dummy analysis,and Monte Carlo bidding searching.In addition to finding the best possible contract,the main objective of bridge bidding is to convey information to other players.Therefore,we first design a bidding system model(BSM)to improve players’communication and exploit the known good bids.Next,we use the hand information provided by BSM mentioned above to design a sampling algorithm,which helps explore bidding choices.The double-dummy analysis efficiently calculates the final contract’s cost to form the rewards for intermediate bidding decisions.Finally,Monte Carlo bidding searching is used to get the best contract.

4.1 Bidding System Model(BSM)

A reasonable and effective bridge bidding system is a vital prerequisite for player communication.The bidding sequence can represent the information the teammates convey,so we can learn all the contents of the bridge bidding system only through the bidding data without directly learning the rules of the bidding system.Therefore,we first use the real bidding data under the natural system provided by the Snyrey platform to train a bidding system model(BSM)based on a deep neural network.Due to the timing characteristics of historical bidding sequences,DNN and CNN structures are not suitable for processing this kind of real bidding data,so we choose RNN as the basic network of our model.The structure of BSM is shown in Figure 2,which consists of two parts,one is a bidding prediction system based on imitation learning,and the other is a visualization system for hand understanding.This visualization system can help players transfer hand information to each other and evaluate the hand’s value to help predict bidding more accurately.Since we only know our hand information in Bridge,the model can only input one player’s hand and then make predictions.Under the current bidding process,a player predicts what bid he should call based on the information conveyed by other players’bidding and his hand.

BSM contains a three-layers stacked Recurrent Neural Network(RNN)and a multi-layer fully connected neural network.To facilitate the description,we first define some symbols shown in Table 2.The input layer accepts the playeri’s handsXi,bidding actionbL,vulnerabilityvand positionp.After getting the embedding vectors,we concatenate them as input of a three-layers stacked RNN.The hidden statesis finally encoded by the RNN,which is as follows:

Table 3.Test case.The actual situation is that the North and South players have nine cards with spade ♠,nine cards with diamond ♢,and the East and West have 11 cards with heart ■.The hands of both sides are very obvious.The North and South players prefer the contract called S and D.It is biased towards the contract called H.After fierce bidding,the West player is the declarer,and the contract is 7H.

whereFs(•) is a recursively called nonlinear activation function of the recurrent neural network.bLrepresents theLthbid in a bidding sequence.

Simultaneously,the outputs of the hidden states encoded by RNN are fed into the multi-layers fully connected neural network,i.e.MLP (Multi-Layer Perception).We then define functionFHmlp(•),FCsuitmlp(•),FYmlp(•)andFGmlp(•)for four types of MLP units.The overall formula in features of external information are as follow.

wheresuit=.

In order to prevent the violation of bridge rules in the bidding prediction,we set up a rule filter vectorPBmask.When a bid violates the bridge rules in a certain state,we define the weight of such bid to 0 so that the rule of Bridge can be gradually learned.We definePBmask(L)as follows:

The output layer of our model consists of a hands understanding system and bidding decision-making.

The visualization system has three outputs: the probability distribution of the HCPs of the teammateP(H=h|Xi,BL),the probability distribution of the number of cards of each suitP(Csuit=c|Xi,BL)and the probability distribution of the hands of the other three playersP(=1|Xi,BL).

By combining Eq.(1),Eq.(2)and Eq.(4),we get the objective functionIof the hand understanding as the manually specified feature.

Note that the primary purpose of bridge bidding is to find the best possible contract and convey some information to partners.So the bidding prediction system describes a bid probability distribution that conforms to the rules of the system based on the features coded by the model and the manually specified feature,in which the objective functionGis as follows:

Figure 3 and Figure 4 respectively show an example of model input and output.We can see that the model’s input is the player’s hands,bidding action,check rules,vulnerability,and position,followed by 3-layers RNN.A 52-dimensional vector represents the player’s hands,and a 41-dimensional vector is used to check rules that ensure the bidding sequence’s rationality.We also add the vulnerability to the input for better score calculation.Besides,one of the most important factors is the position,which means whether one’s turn to bid.The importance of this factor will be demonstrated in the experiment later.

4.2 Sampling Algorithm

As bridge bidding is an imperfect information problem,it is challenging to build a model to correctly predict the opponent’s actions without knowing the opponent’s hands.Therefore,we design an algorithm for hand sampling based on the information provided by BSM mentioned above.This efficient Monte Carlo sampling algorithm can quickly generate the hands that align with the current bidding process,thereby perfecting the imperfect information in the bridge game.

This algorithm contains three steps to ensure that each player has 13 hands.It first generates the 13 hands of teammates,then generates the opponent’s hand,and finally,additional filters.Algorithm 1 describes how to generate a teammate’s hand sampling based on the teammate’s hand characteristics.Algorithm 2 describes how to sample the hands of the remaining two players.Since the two opponents belong to the same team,their specific hands have little effect on the result.Therefore,in Algorithm 2,we first sample the hand of one of the players based on the mean of the probability that two opponents hold the same card’Y’,and then the remaining 13 cards belong to the other player.Furthermore,to discard the hands that are entirely inconsistent with the system’s rules caused by the small probability sampling,it is necessary to filter the sampled hands to ensure the reasonableness of the sampling.

Algorithm 1.The algorithm of teammate’s hands sampling.Require: the set of hands to be excluded: Xi,PH,PC Ensure: teammate’s hands: Xteammate 1: function SAMPLE HANDS(Xi,PH,PC)2: allcard ←the set of all cards;3: card ←allcard−Xi;4: Xteammate ←∅;5: H ←sample with PH;6: combineset ←all sets of HCP with H 7: combineset ←combineset−the sets conflicting with Xi 8: if combineset=∅then 9: fail,go to 2 10: end if 11: Xteammate ←randomly select from combineset;12: C■,C♠,C♢,C♣←sample with PC;13: if C■,C♠,C♢,C♣complained with Xi then 14: fail,go to 2 15: end if 16: card ←card-all high cards 17: for suit in{■,♠,♢,♣}do 18: Xteammate ←Xteammate+randomly draw Csuit cards corresponding to the suit from card 19: end for 20: return Xteammate.TEAMMATE

Algorithm 3 shows the final sampling algorithm,which first generates samples that require five times the number of samplesKthrough Algorithm 1 and Algorithm 2,and then scores these samples through a secondary verification function,and finally selects theKsamples with the highest scores,thereby improves the quality of sampled samples.The probability distribution obtained according to the Eq.(6)can express the confidence of a bidding process corresponding to a bid under a certain system:PtrustX(bL).The secondary verification algorithm scores the sampled hands by the degree of confidence,and the scoring formula is:

Algorithm 2.The algorithm of opponents’hands sampling.Require: the set of hands to be excluded: Xexists,PYi ;Ensure: Xopp1,Xopp2.1: function SAMPLE HANDS(Xexists,PYi )2: allcard ←the set of all cards;3: card ←allcard−Xexists;4: Xopp1,Xopp2 ←∅;5: for Y in card do 6: P ←(PYopp1+PYopp2)÷2;7: rnd ←0 to 1 random floating point number;8: if rnd ≤P then 9: Xopp1 ←Xopp1+Y 10: else 11: Xopp2 ←Xopp2+Y 12: end if 13: end for 14: return Xopp1,Xopp2.OPPONENTS

Algorithm 3.The algorithm of sampling based MTCL.Require: Xi,BL,PH,PC,PYi ,K;Ensure: result:{Xn1,Xn2,Xn3,Xn4 |1 ≤n ≤K}.1: function SAMPLE HANDS(Xi,BL,PH,PC,PYi ,K);2: K ∗5 ←first sample size;3: result ←∅4: for i ←1 to K ∗5 do 5: Xteammate=function SAMPLE HANDS (Xi,PH,PC);6: Xopp1,Xopp2=function SAMPLE TEAMMATE OPPONENTS HANDS (Xi,PYi );7: result ←resutl+{Xi,Xteammate,Xopp1,Xopp FBL score(Xi,Xteammate,Xopp1,Xopp2)};8: end for 9: sort the elements in the result from large to small by FbL score;10: result ←Take the first K elements of the result;11: return result.2,

where 0< γ <1 is a parameter that balances the bidding process and the influence.With the advancing of the bidding process,the bidding system has less and less binding force on the bidding,so the impact of the system confidence on the score is also more negligible.

4.3 Double Dummy Analysis with Neural Network(NN-DDA)

Given the assumption that all four players have exposed their deals (e.g.,everyone knows the deals of others) and each player adopts the optimal strategy,double-dummy analysis (DDA)3means calculating the maximum number of tricks that can be made in the contract of every suit.It is possible to estimate a player’s score in the play stage at high speed with the contract known by DDA.In the whole bidding model,DDA can evaluate the bidding process and results obtained by Monte Carlo searching algorithm to screen out the best bid.In previous studies,the results of DDA are obtained by calling the open-source library python-dds.Although calling python-dds can get accurate DDA results,it costs hundreds of milliseconds to calculate one deal,which is not conducive to processing lots of deals obtained by Monte Carlo sampling.Therefore,we train a dense neural network(DNN) model using the DDA results of python-dds as the expert experience to handle numerous samples.The model comprises a multi-layer fully connected neural network and is trained using a backpropagation algorithm and stochastic gradient descent algorithm.It can simultaneously analyze considerable deals to significantly reduce the time cost of calculation.As shown in Figure 5,the input of the NN-DDA model is the deal vector of all players,and the output is DDA results:

Algorithm 4.Bidding by MTCL.Require: (Xi,BL,PH,PC,PY,K);Ensure: bid result.1: function MTCL BIDDING(Xi,BL,PH,PC,PY,K);2: sample cards ←function SAMPLE HANDS(Xi,BL,PH,PC,PYi ,K);3: bid result ←∅4: for next bid in all bids do 5: bL+1 ←bL+next bid;6: bid score ←0 7: for X1,X2,X3,X4 in sample cards do 8: completed bidding ←BSM;9: double dummy ←sdda;10: bid score +Fbid score←bid dum 11: end for 12: bid score(completed bidding,double result +{next result←bid score};13: end for 14: bid bid,bid score;15: bid result sequence by bid result ←top 1;16: return bid result.my);

whereX={X1,X2,X3,X4}.

4.4 Monte Carlo Searching Algorithm

The complete searching process is depicted in Algorithm 4.The searching algorithm first obtains a large number of cards through hand sampling and,at the same time,traverses all legal next bids.Next,it uses the proposed BSM to quickly complete the bidding process(completed_bidding)to get the fnial contract(bfinal).Then the final score of the current bidding process can obtain through NN-DDA at a high rate of speed.Finally,we use the score of the final contract to estimate the cost of intermediate bidding decisions.The following function calculates the evaluation score:

whereimp(•) is a common scoring function in Bridge.

V.EXPERIMENT

Before presenting the experimental results,we introduce the dataset and the performance of BSM and NNDDA in each setting.Finally,we make further analysis and discussion.

5.1 Dataset

The dataset used in the experiment is provided by the Snyrey platform.The Snyrey platform has accumulated a historical record of nearly 500 million bids and doubles results.We randomly select nearly 8,000,000 real bidding instances as our data set,70% of which are used as training data for the physical bridge model,20% of which are used as the validation set,and the rest as testing data.The information of each instance recorded in the dataset includes four parts:the player’s card,historical bidding sequence,vulnerability,and double-dummy results.

We analyze to verify the rationality of the dataset,shown in Figure 6.According to Figure 6a,the proportion of the major-suit and no-trump contracts is relatively large.The contracts are always at the level of 3 and 4.This contract method is consistent with the behavior of human players because of the more raw scores.Figure 6b-6d show that the probability of each card in each player is roughly the same.Moreover,the average HCP of each player is 10,which proves that our dataset is balanced and reasonable.Figure 6e basically presents a normal distribution.Most bids are concentrated at the end of 8∼13,and the bid sequences that are too long or too short are rare in real bridge games.In short,it is feasible to train the model through this dataset.

5.2 Performance of BSM

We design BSM based on deep neural networks.All of our models are run on a single GPU,with roughly a runtime of 20 minutes per epoch.We run all the models up to 30 epochs.

5.2.1 Compared Methods

First of all,we adopt two network structures,RNN and LSTM.As shown in Figure 7,there is a large gap between the model using RNN and the model of LSTM.The accuracy of BSM-LSTM is much higher than BSM-RNN for each bidding prediction,especially in the substantive bid.The average accuracy of BSM-RNN is about 76.19%,while the average accuracy of BSM-LSTM can reach 94.12%.We have further evaluated the performance of BSM-RNN and BSM-LSTM.There are other metrics,such as precision and recall.Figure 8 shows the comparison results still show that BSM-LSTM achieves the optimal results under the same settings.Furthermore,we evaluated the number of hands in each suit,as shown in Figure 9.The predictions of the two models for high flowers (spades♠,hearts) are more accurate than low flowers (diamonds♢,clubs♣).In most bridge bidding systems,there are more rules for high-suit information in hand than for low-suit information.Therefore,it is easier to learn more feature information of high-suit hands from the training data.Besides,the MAE of BSM-LSTM is lower than that of BSM-RNN in different suits.In summary,we choose LSTM as the optimization of our model.

As for LSTM representation,three main hyperparameter selections are conducted using crossvalidation techniques based on the kl-means and focalloss.This includes learning rates(constant=0.001 or decreased according to linear or exponential schedule),hidden layer dimensions,number of hidden layers.We evaluate the model on validation sets by precision,recall,f1-score,and accuracy to choose the best parameters.Finally,we employ a 3-layers LSTM with 512 hidden state sizes in our experiments.

5.2.2 The Evaluation of Visualization System

In order to show the output of BSM more intuitively,we have made a visualization system that can reflect the distribution of bid prediction,player hands,HCPs,and card numbers–taking an example to illustrate it.We select a representative bidding process to analyze and verify the visualized results and evaluate whether the visualized results can correctly express BSM’s understanding.For ease of presentation,in the analysis of experimental results,C,D,H,and S are uniformly used to represent suits♣,♢,,♠,and N represents no-trump card.The hands of each player in the test case are represented by a string separated by dots,which in turn represent the cards of the suits♣,♢,,♠held by a player.

Table 3 shows that the North player first opened 1D.In the natural system,1D is an open-bid,which means that the North playeri’s HCPs exceeds 12 points and 4♢tricks.Moreover,we can see from the hands that the North player has 13 HCPs,so according to the bidding system rules,1D should be opened.When the teammate of the North player,the South player,receives this open bid,he or she should understand the above information.Figure 10a shows the probability distribution of average HCPs of the North player predicted by the South player after getting the open-bid 1D.It is not difficult to see that the South player indicates that the probability of the North player’s big card points is between 12-14,which conforms to the rules of the natural system.

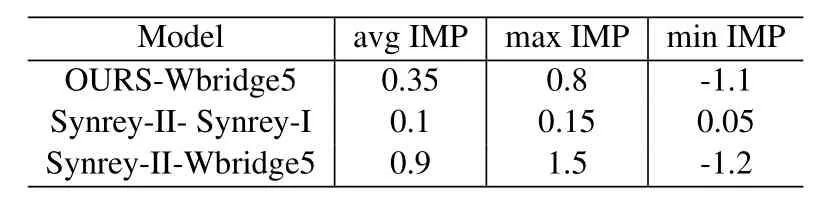
Table 4.Bidding strength comparision.

Next,let us analyze the visualization results generated when the contract is finally obtained.Figure 10b shows that the North player predicts that the South player has 7-8♠cards,0-1cards,2-3♢cards and 2-3♣cards,and the real cards of the South(7♠cards,1card,3♢cards,2♣cards)are very close.Judging from the prediction results of the distribution of the South player (Figure 10c),there is a high probability of having a lot of♠cards.Furthermore,we can see that BSM successfully predicted that the South player might have 2-3♢cards and the feasibility of the A card.In fact,the South player does own the A card.In brief,it indicates that BSM can accurately predict the information transmitted through the bidding and reasonably generate hand understanding for players to communicate.

5.3 The Performance of NN-DDA

As we mentioned above,NN-DDA helps to process a large number of sampled hands quickly.To evaluate its performance well,we take the result of python-dds as the standard,which shows the accuracy rate of NNDDA is 81.56%.Besides,the predictions account for 99.62%,which have gaps with the result of python-dds lying in [-1,1].It takes NN-DAA 9.5137s to predict 2,000,000 deals in the mean rate of 210,222.2139 deals/s,while python-dds will spend 328.3738s to calculate 2,000 cards randomly selected from the 2,000,000 deals above,which implies the mean rate of calculating is 6.0906 deals/s.It can be learned that the model can significantly improve DDA speed with similar accuracy to python-dds.Thence it is suitable to analyze a large number of deals in a short time.

5.4 The Performance of Searching Strategy

In order to evaluate the performance of our search,we compare it with the program Wbridge5,the champions of the World Computer Bridge Championship 2016-2018.We can see that in Table 4,our searching strategy outperforms Wbridge5 by 0.15 IMP.At the same time,our model brings the possibility of tree searching for imperfect information games.In 10,000 games,using our model for tree searching to assist Synrey-II in playing Bridge wins 1000 IMPs more than Synrey-I,which defeats the runner-up in the World Computer Bridge Championship 2017-2019.

VI.CONCLUSION

In this paper,we propose an enhanced strategy that combines deep learning with Monte Carlo searching.It is mainly divided into four parts: bidding system model,sampling algorithm,double-dummy analysis with the neural network,and Monte Carlo searching algorithm.BSM includes a preliminary bidding prediction system and visualization system.The player needs to explain the information conveyed by his bid in the natural bridge competition.Nevertheless,it is difficult for the neural network to explain why it is called the bid.Therefore,our visualization system allows people to intuitively understand the hands’information after the machine makes a bid,which is convenient for researchers to study in-depth research of algorithms and models and provide a basis for further searching within the bridge system.We believe extending our approach to learn more imperfect information games is possible.

In future work,we will try to use reinforcement learning to improve further the searching strategy on the mobile applications of multi-agent communication.Besides,studying when to retrain and rationally use edge server resources is also the focus of research.

ACKNOWLEDGEMENT

This work was supported by the Funds for Creative Research Groups of China under No.61921003 and Snyrey Bridge Company.

NOTES

1http://www.wbridge5.com/

2High Card Points-total points of a full deck of cards.A=4,K=3,Q=2,J=1.The total number of HCPs is 40,and the expected number of HCPs in the given hands is 10.

3http://bridgecomposer.com/DDA.htm