Environment Information-Based Channel Prediction Method Assisted by Graph Neural Network

Yutong Sun,Jianhua Zhang,Yuxiang Zhang,*,Li Yu,Qixing Wang,Guangyi Liu

1 State Key Lab of Networking and Switching Technology,Beijing University of Posts and Telecommunications,Beijing 100876,China

2 Future Research Laboratory,China Mobile Research Institute,Beijing 100053,China

Abstract: Recently,whether the channel prediction can be achieved in diverse communication scenarios by directly utilizing the environment information gained lots of attention due to the environment impacting the propagation characteristics of the wireless channel.This paper presents an environment information-based channel prediction (EICP) method for connecting the environment with the channel assisted by the graph neural networks (GNN).Firstly,the effective scatterers (ESs) producing paths and the primary scatterers (PSs) generating single propagation paths are detected by building the scatterercentered communication environment graphs (SCCEGs),which can simultaneously preserve the structure information and highlight the pending scatterer.The GNN-based classification model is implemented to distinguish ESs and PSs from other scatterers.Secondly,large-scale parameters (LSP) and small-scale parameters (SSP) are predicted by employing the GNNs with multi-target architecture and the graphs of detected ESs and PSs.Simulation results show that the average normalized mean squared error (NMSE)of LSP and SSP predictions are 0.12 and 0.008,which outperforms the methods of linear data learning.

Keywords: channel prediction; propagation environment;graph;scatterer detection;GNN

I.INTRODUCTION

With the commercialization of fifth-generation (5G)networks worldwide,research into sixth-generation(6G) networks has been developed to deal with the demands of increased technologies and communication scenarios.Especially to support the future digital society,the 6G network faces the great challenge of working efficiently and flexibly in a broader range of scenarios[1].The traditional way of system design is to sequentially get the channel model of typical scenarios first and then do the network design by offline simulation,which leads to a 6G network lack of adaptation to dynamic environments.Thus,efficiently acquiring the precise channel for changing environment becomes crucial,significantly influencing further applications[2,3].In practice,predicting the large-scale parameters (LSP) and small-scale parameters (SSP)that mainly affect the received signal power of a specific environment enables the algorithms design and further applications[4–9]in diverse scenarios.

The traditional prediction methods are based on historical data,which leverage the collected data to predict future ones,and the potential channel correlation has to be evaluated through digging from the previous information [10,11].However,the internal correlation between different channels is difficult to obtain in diverse environments,rendering it challenging to implement.With the development of advanced machine learning (ML) techniques,neural networks(NN) have been introduced to the physical layer and power the methods designation for reliable prediction models [12,13].Different learning approaches are utilized for accuracy improvement,such as long short-term memory (LSTM) [14],convolutional neural networks(CNN)[15]and artificial neural networks(ANN) [16,17].Moreover,the location information[18]can be utilized in the learning phase,and predictions can be achieved at other locations.However,without considering the fast-varying physical environments is inconsistent with the actual communication situation,in which the channel changes with the dynamic environment.

With the rapid development of sensing techniques,environmental information can be obtained with the aid of sensing enhancement.The environment-based channel modeling methods for higher precision and lower computational costs are proposed in [19,20],which abstracts the environment and channel characteristics to explore the environment-channel connection.For LSP prediction,satellite images could offer improved performance with the assistance of deep learning(DL)techniques[21,22].The latitude,longitude,elevation,and distance were considered the input of the ANN in[23]to acquire the accurate path loss in a high-frequency band.By utilizing the extracted environment features,the multilayer perceptron (MLP)is employed to predict the path loss [24].Similarly,ML-based path loss prediction works are presented for urban,suburban,rural,aircraft cabin,and multitransmitter signal propagation environments [25–29].Moreover,for spatiotemporal channel parameters prediction,which includes delay spread (DS),azimuth angle spread of arrival(ASA),azimuth angle spread of departure(ASD),zenith angle spread of arrival(ZSA),and zenith angle spread of departure(ZSD),the spherical depth images are used in [30]by CNN method,and[31]predicts by leveraging the SSP directly.However,the methods of propagation environment utilization are always focused on the LSP prediction and only introduce basic information to improve the precision but lack whole environment structure preservation.

Unlike the images and vectors in Euclidean space,graphs are nonlinear that can represent more complex structure data,such as molecules and social networks.Therefore,representing it with graphs is more appropriate for the structural propagation environment,which can help preserve the layout information.However,learning with graph data requires specific graph representation and learning methods[32].Graph neural networks(GNN)aroused great attention for graph learning,which is considered a vital technique that is adept at processing structured data inputs [33,34].GNNs generally follow a recursive neighborhood aggregation scheme,where each node aggregates feature vectors of its neighbors to compute new feature vectors [35].In [36,37],the propagation graphs and GNNs are leveraged to provide a flexible structure for hybrid channel model construction that models multilink channels with account for multiple scattering.Inspired by those works,we believe that graph data and GNN-based learning methods are feasible techniques to cope with the channel prediction issue by leveraging the environmental layout information and considering the environment as a graph.

This paper focuses on the channel prediction method involving LSP and SSP prediction.An environment information-based channel prediction(EICP)method is presented to directly connect the environment to the channel by constructing environment graphs and building the mapping based on the GNN model.The main contributions and novelties of this paper are summarized as follows:

• A two-step EICP method is proposed for LSP and SSP prediction,which can be performed with two main modules: scatterer detection and scatterer detection-based channel prediction.

• The scatterer detection module achieves effective scatterers (ESs) and primary scatterers (PSs) detection for collecting the scatterers that produce paths and single propagation paths,respectively.In practice,the scatterer-centered communication environment graphs (SC-CEGs) are constructed for each scatterer to be detected and implement the graph classification based on the GNN using the built graphs as input.

• The channel prediction module accomplishes the LSP and SSP prediction for the environment and primary paths,respectively.According to the detected ESs and PSs,the fully-connected propagation environment graphs (FC-PEGs) and singleconnected propagation environment graphs (SCPEGs)are generated for corresponding graph representation.Then,to cope with the multiple related parameters prediction,a GNN-based multitarget regression model is built to exploit the correlations.

The remainder of this paper is organized as follows.Section II introduces the problem formulation and architecture of the proposed EICP.A detailed description of the scatterer detection method is presented in Section III.Section IV gives the scatterer detectionbased LSP and SSP prediction methods.The simulation results and performance evaluations are presented in Section V.Section VI concludes this paper.

II.PROBLEM FORMULATION AND ARCHITECTURE

2.1 System Model

In this paper,we focus on the system of multiple-input multiple-output (MIMO).For the downlink transmission,if v∈CM×Ndenotes the downlink precoding vector,the received signal at the mobile user can be expressed as

whereyis the received signal,sdenotes the transmitted signal,andnstands for the receive noise.H represents the downlink channel,w∈W and v∈V are the beamforming vectors of transmitter(Tx)and receiver(Rx),which can take one of the candidate values collected in the codebook W and V.The channel matrix H can be written as

whereLis number of paths,andβl,φl,andτlare path gain,angle,and delay of thel-th path,respectively.arxand atxare the antenna radiation patterns of Rx and Tx,respectively.

2.2 Physical,Communication and Propagation Environments

The environment should be different from the wireless channel perspective in various stages.As shown in Figure 1,the physical environmentSshould be the environment of objective existence without the specific interactions between objects,which can be described with the basic information of the environment with no limitation,i.e.,S={size,position,function,color,structure,...}.

When the Tx and Rx are set,the environment can be defined as the communication environmentC,where internal objects are no longer independent but interact by producing different paths according to the diverse propagation mechanisms,such as line-of-sight(LOS) transmission,reflection,and diffraction [38].The electromagnetic wave from Tx will interact with scatterers before arriving at Rx.Each path is determined by the geometric relations of the Tx,Rx,and acting scatterers.Therefore,the essential information thatCfocuses on is only the geometry-related size and position as well as the geometric structure ofC,i.e.,C={size,position,structure}.The attributes like function and color are no longer taken into account,which is not related to the propagation.

However,not all scatterers play a role in the process of wireless communication.The scatterers that produce paths and influence the channel characteristics can be defined as effective scatterers (ESs).On the contrary,the uninvolved scatterers can be presented as invalid scatterers (ISs).Compared toC,the environment that considers the effective scatterers only can be known as the propagation environment,which can be described asP={sizees,positiones,structure}.

Meanwhile,the propagation paths are not equally important.Except for the LOS path,the single propagation paths are primary paths,which significantly impact the channel[39]compared with the paths caused by the multiple propagation mechanisms.The precise detected single reflection and diffraction paths can approximately represent the channel with much lower complexity.In other words,the scatterers with single propagation points can be considered the primary scatterers(PSs),and the other scatterers can be defined as the non-primary scatterers(NSs).

2.3 Environment Graph

For the simultaneous representation of features and complex structure,the nonlinear graphs are more appropriate than the linear data in Euclidean space.Hence,the communication and propagation environments are represented with the corresponding environment graphs,which can provide a flexible way to track the spatial relations of scatterers within a specific environment.In the environment graph,nodes usually represent Tx,Rx,and scatterers,and edges represent geometrical transformations between the nodes.The actual size and position information of scatterers can be represented as the node feature vectors.

Therefore,it can be assumed that there is a oneto-one mapping between the propagation environment and channel.To simultaneously preserve the basic and structure information of scatterers and the whole environment,the graph data structure is utilized to represent the propagation environment.LetGp(Vp,Ep)denote a propagation environment graph with nodesVp,edgesEpand node feature vectorsXvforv ∈Vp.Thus,the one-to-one mapping can be described as

whereM(·)represents the mapping function.

2.4 Architecture

In this paper,we present a novel EICP method by considering the environment structure and learning the mapping of constructed environment graph and the channel by developing GNNs.The EICP method consists of two main modules: scatterer detection and scatterer detection-based channel prediction,where the second part includes the ES-based LSP prediction and PS-based SSP prediction,as shown in Figure 2.

The scatterer detection module consists of ES and PS detection,respectively,by building the SC-CEGs for representation in the geometric structure of a specific communication environment.To highlight the scatterer to be detected,the SC-CEG considers Tx,Rx,and scatterer as nodes and defines the edges by the undirected connection between the node to be detected and other nodes,where each node has a feature vectorX.The proposed graph design method can maintain the environment structure information and emphasize the scatterer to be detected simultaneously.

To deal with the detection issue as a classification problem,the GNN-based classification model is constructed for discriminating ESs/PSs from ISs/NSs by capturing the different types of graph structures.As shown in Figure 2,three SC-CEGs are formed for the environment of three scatterers,and then the trained classification model can output the results of each graph,i.e.,ESs={v1,v2},and IS={v3}for effective scatterer detection; PSs={v1},and NSs={v2,v3}for primary scatterer detection.

After collecting the scatterers that embody the essential information of channel generation,the LSP and SSP prediction methods are studied.For LSP prediction,the FC-PEGs with the Tx,Rx,and the selected ESs are defined for propagation environment representation.The FC-PEGs are constructed with undirected edges of each node and corresponding feature vectorX,which includes the additional propagation-related feature compared to theXof SC-CEG.

For the one-to-one mapping between FC-PEG and corresponding LSP,including path loss,root-meansquare (RMS) DS,ASA,ASD,ZSA,and ZSD,the GNN-based multi-target prediction model is designed by training different outputs simultaneously at the beginning stage.The jointly training scheme enables the preservation of the embedding feature that contains the essential representation of all the targets.

Similar to the LSP prediction method,the primary scatterer-based method is proposed for SSP prediction of the main paths by constructing the SC-PEG with each PS.In view of the correlation between the SSP,such as power,delay,azimuth angle of arrival(AOA),azimuth angle of departure(AOD),zenith angle of arrival(ZOA),and zenith angle of departure(ZOD),the GNN-based multi-target prediction mode is built for getting the parameters of the main paths.

III.SCATTERER DETECTION

This section presents the detailed scatterer detection method,which can obtain the effective and primary scatterer by communication environment structure learning.Moreover,the scatterer classification model is introduced based on the GNN in order to establish the mapping relationship between the graphs and different types of scatterers.

3.1 SC-CEG Construction

To determine whether a scatterer is playing a role in wireless propagation,only relying on the scatterer level information is insufficient,which needs the structure level message of the communication environment from the knowledge integration of internal scatterers.Due to the limited environment and no propagation-related information,it is difficult to classify all the scatterers by constructing one environment graph alone.

The communication environment graph is defined from the perspective of the pending scatterer by outlining the interaction with other nodes for the signature needs of the scatterer under detecting.Compared with adding the signature in the feature vector of nodes for telling the difference between the scatterers to be detected and other scatterers,emphasizing the target by constructing different edges can further influence the message transmission inside the graph at the structural level.Hence,for an environment withnscatterers,ndifferent SC-CEGs will be constructed.

The SC-CEG is constructed by building edges between the pending scatterer node and the other nodes.The SC-CEG withnscatterers can be defined asGc=(Vc,Ec).Vcincludes the Tx nodevt,Rx nodevr,andnscatterer nodesv1,v2,...,vn,which can expressed asVc={vt,vr,v1,v2,...,vn}.Ecconsists of all the edges inGc.One SC-CEG of environment sample with total 5 scatterers and pending scatterer nodev3is shown in Figure 3.In this SC-CEG,Eccan be expressed asEc={(vt,v3),(vr,v3),(v1,v3),(v2,v3),(v4,v3),(v5,v3)}.

For each node,the attributes can be denoted asXcfor feature vector representation.The geometric attribute ofvtandvrare spatial position,hence the corresponding feature vectorXtandXrcan be described asXt=(xt,yt,zt) andXr=(xr,yr,zr),where (xt,yt,zt) and (xr,yr,zr) are the coordinates of Tx and Rx.As for scatterer node,also the basic information are adopt,i.e.,the center coordinate(xi,yi,zi),the longli,widthwi,and heighthiare considered the feature vector,which can described asXi={(xi,yi,zi,li,wi,hi),i=1,2,...,n}.

3.2 GNN

In terms of the proposed environment graph representation learning,GNNs are utilized to build the one-to-one mapping between the constructed environment graph and the corresponding channel parameters.GNN is a deep learning method for dealing with such structured data,which uses the graph structure and node featuresXvto learn a representation vector of the entire graphhG.In general,GNNs follow a neighborhood aggregation strategy [40,41],which iteratively updates a node’s representation by aggregating adjacent nodes’representations.

There are two basic operators for GNNs.One is the Aggregate(·),which can serve as the aggregation function of the neighborhood information.Themean,sum,andmaxfunctions are often considered as the basic aggregation operators,while sophisticated pooling and normalization functions can also be designed.The other is Combine(·),which passes the aggregated node feature to a learnable layer to generate node embedding for the GNN layer.

As a result,the representation of nodesa(k)vcaptures the structural information within itsk-hop network neighborhood inkiterations of aggregation.Thek-th layer of a GNN can be expressed as

whereh(k)vis the feature vector of nodevat thek-th iteration,fork=1,2,··· ,KandN(v) is a set of nodes adjacent tov.Theh(0)vis initialized withXv.

3.3 GNN-Based Scatterer Classification

To achieve the optimal scatterer detection performance,we construct a graph classification model for distinguishing different graph structures by mapping them to different representations in the embedding space.The GNN architecture of the scatterer classification model is shown in Figure 4,in which the fundamental algorithm is implemented with the graph isomorphism network(GIN)proposed in[32].

As for the binary classification problem of graph,where,given a set of communication environment graphs{CEG1,...,CEGn} ⊆CEGand their corresponding labels{y1=0,y2=1} ⊆Yin a environment,we aim to learn a representation vectorhCEGthat helps predict the label of an entire graph,yCEG=g(hCEG).

For aggregating the neighbors,the Aggregate(·)is implemented with sum aggregators over a multiset,which has been proved to have better performance than the max and average methods.Therefore,thea(k)vcan be formulated as

whereWis a learnable matrix,and SUM represents an element-wise sum-pooling.

For graph representation learning,MLPs are utilized.Thus the GNN can update the node representations as

whereϵis a learnable parameter.

Moreover,to obtain the representation of the entire graph,the Readout(·) function is utilized to aggregate node features from the final iteration.Thus,the graph representation with Concat(·)that are concatenated across all iterations of GIN is

There are 8 MLPs deployed for graph learning.For each MLP,there are 3 hidden layers with 256 neurons,which are implemented with bach normalized(BN) [42]for smoothing the optimization landscape and rectified linear unit (ReLU) [43]for activation.Note that the input layer of the first MLP should be identified with the features of the graph with dimensions.After graph learning,the fully-connected network is utilized to obtain the scores of two classes by inputting the embedding representations learned from each MLP.The results will be rejected with dropout[44]to prevent overfitting and increase generalization.

IV.CHANNEL PREDICTION

After detecting the ESs and PSs of one specific environment,we assume that all the retained scatterers participate in producing paths,i.e.,the propagation environment generated by the ESs or PSs can determine the channel.However,the paths caused by different propagation mechanisms need complex calculations in the ray-tracing process.A complete propagation process between Tx and Rx is highly complicated in the real case,considering the involved scatterers,electromagnetic propagation type,and the number of occurrences simultaneously.To simplify the problem,we consider the propagation on the global view to deal with LSP and SSP prediction.

4.1 ES-Based FC-PEG Construction

For representing the globel structure of the environment and preventing the problem on the complex path level,the FC-PEGs are constructed to predict the LSP.We assume the FC-PEG asGf=(Vf,Ef).TheVf={vt,vr,v1,v2,...,vm}wheremrepresent the number of effective scatterers andv1,v2,...,vmdenote themscatterer nodes inGf.Efpresents all the edges of each two nodes.Figure 5 shows a FC-PEG with the selected effective scatterers nodev3andv4.In addition to the fundamental geometric attribute utilized in the SC-CEG,the blockage feature of each scatterer is abstracted for accuracy improvement of channel prediction by taking blockage characteristic[45]into account,defined as blockage featurebi.The feature is calculated by the coordinates of Tx,Rx,and scatterer,which represent the blockage degree that thei-th scatterer occludes the LOS[46].

The distance between the center point ofi-th scatterer and LOS is calculated.Thenbican be defined as the ratio of the obtained distance and the width of thei-th scattererwi.Therefore,for each scatterer node in FC-PEG,the feature vector can be expressed asXi=(xi,yi,zi,li,wi,hi,bi);i=1,2,...,m,as shown in Figure 5,whereb3andb4denote the blockage feature ofv3andv4.

4.2 PS-Based SC-PEG Construction

The SC-PEG is formed with the detected PS,which can produce a single reflection or diffraction path.Therefore,the graph only consist of three nodes:vt,vr,and the primary scatterer nodevp.Similar to the FC-PEG construction scheme,letGp=(Vp,Ep)indicate a SC-PEG,whereEf={(vt,vp),(vp,vr)}and the feature of the primary scatterer node isXp=(xp,yp,zp,lp,wp,hp,bp).An SC-PEG sample with the detected PS nodevpis indicated in Figure 6.

4.3 GNN-Based LSP and SSP Prediction

According to the built FC-PEGs and SC-PEGs,the GNN-based graph regression method is implemented for continuous channel parameters prediction.The multi-target channel prediction model is presented by learning the different embeddings of the same graph to cope with the multiple related outputs and leverage the correlations together.

Multi-target regression,also known as multi-output regression,refers to the task of predicting multiple continuous variables using a common set of input variables [47].Motivated by the learning schemes of stacked single-target proposed in[48],the multi-target channel prediction method is presented by processing the compound dependencies between the multiple features and target variables.The joint training diagram considers not only the underlying relationships between the features and the corresponding targets but also the relationships between the targets.

The procedure of the multi-target channel prediction model is shown in Figure 7.Multiple labels are associated with each instance.Therefore,we have the constraint ofY ⊆Rm,where Rmis an mdimensional output label space,given an unseen graph instancePEG ⊆PEG,the learned multi-target regression functionf(·) predicts a real-valued vectorfm(PEG)⊆Ymas the output.

In order to leverage the correlations of the targets,the two stages training scheme is designed.In the primary stage,the embedding representations that contain the graph features are collected by training with the data of each couple of graphs and targets.Then,all the representations and the original graphs are concatenated as the input of the second training stage.As a result,representations of the related targets work together in each target prediction learning process.The MLPs are used as the fundamental architecture of the involved GNNs,similar to the scatterer classification model.

V.SIMULATION RESULTS

This section presents the simulation results to verify the proposed EICP method,including scatterer detection,LSP,SSP,and system performance.

5.1 Dataset

The dataset contains environment samples and corresponding channel data[46].The channel is produced by the commercial RT tool WirelessInSite.In order to obtain a large number of environmental samples,which can be automatically generated and conform to the input format of WirelessInsite,the 3D modeling software Blender with python scripting interface is utilized for environment samples generation.Then the corresponding channel is produced for each sample by WirelessInSite.

The length,width,and height of the propagation area are set at 15,10,and 3 m.In which Tx and Rx are set on the two sides of the diagonal.Regular scatterers with random numbers,positions,and dimensions are generated with the preset area restriction.More than that,different scatterers are guaranteed disjoined by judging overlap during the generation process.The dataset includes samples of internal scatterers withJ ∈[3,12]numbers.Figure 8 represents a data sample with randomly distributed scatterers.

After random selection,samples with 3,5,6,7,9,10,and 11 scatterers are set for training data,while the testing data are the samples with 4,8,and 12 scatterers.As a result,4566 and 842 environment data are preserved for training and testing,respectively.The channel data are generated at 28 GHz by setting the WirelessInsite with six order reflections and one order diffraction.

5.2 Scatterer Detection Results

Since each scatterer produces a sample,there are 29495 and 5758 samples for training and testing,respectively.The precision and the receiver operating characteristic curve(ROC)are utilized to evaluate the classification model’s performance of the proposed scatterer detection.Moreover,the accuracy results of environment level are illustrated for overall observation.We get 0.9 and 0.92 classification precision for the ES and PS detection,where the precisionprecan be calculated as

The true-positive (TP) and true-negative (TN) represent the true samples that are classified as positive and negative samples,respectively.

Moreover,for the comprehensive assessment of the positive and negative results,we plot the ROC with false-positive rate(FPR)and true-positive rate(TPR),which can be expressed as

where the false-positive (FP) and false-negative (FN)denote the false samples that be predicted with positive and negative.The crucial feature of ROC curve is the area,where the identity ability is more potent as the area grows.As shown in Figure 9,the area of the ROC curve for ES and PS detection are 0.9 and 0.91,which characterize the discriminative power of the proposed GNN-based scatterer detection method,where the closer area is to 1,the better the performance.

Figure 10 shows the test results of the scatterer detection accuracy of environments.It can be seen that more than 30% of environments get all the scatterers correctly classified,and most of the environments have accuracy over 70%.The results show that the PS detection a little outperforms the ES detection.We assume that the geometric representations of PSs are more evident than ESs,in which the scatterer with low height and far away from the LOS can more likely be the ES than the PS.As for time cost,only 2 minutes and 0.0002s are needed for training and one environment sample prediction,respectively.All the training and testing are implemented on one NVIDIA GeForce RTX 2080.

5.3 LSP Prediction Results

The performance of the channel prediction method is evaluated in normalized root mean squared error(NMSE) and cumulative distribution function (CDF)for LSP and SSP prediction methods,respectively.There are 4566 and 842 samples for training and testing,which have the same quantity as the original generated environment samples.

Moreover,to illustrate the performance of the GNN,we compare it with CNN and DNN.There are 5 layers constructed in CNN,and for each convolution layer,64,32,and 16 convolution filters of size 2×2.The rest of the default parameters are the same as that for GNN.The feature vectors of each node form the input data of CNN.For LSP prediction,the matrix data shape is (m+2)×6,where there are Tx node,Rx node,m effective scatterer nodes,and 6-dimensional features for each node.Similarly,for SSP prediction,the matrix shape is 3×7,where there are three nodes and 7-dimensional features for each node.As for the DNN model,the MLPs in GNN are implemented,and the input data is the sequence form of the corresponding input data of the CNN.

As for the DNN model,the MLPs utilized in the GNN are implemented,i.e.,8 MLPs with 3 hidden layers and 256 neurons for each layer.The input data of DNN is the sequence form of the corresponding input data of the CNN model.The NMSEs of ELSP-gt(using the ground-truth ESs),ELSP (using the detected ESs),CNN (using the ground-truth ESs),and DNN(using the ground-truth ESs) are presented in Table1 for each LSP,i.e.,path loss,RMS DS,ASA,ASD,ZSA,and ZSD.The NMSE of testing results can be calculated as

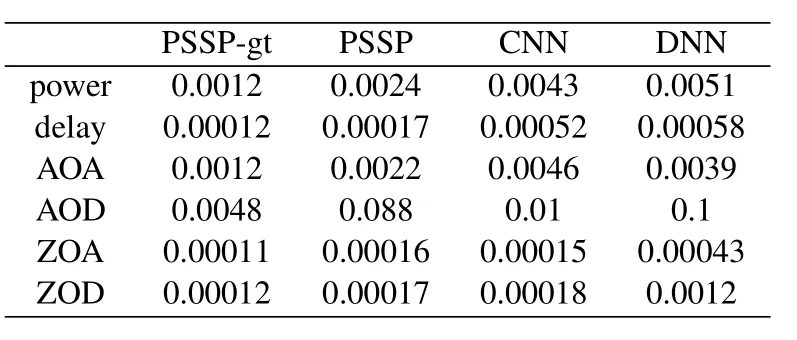
Table 2.NMSEs of PSSP-gt,PSSP,CNN and DNN for SSP.

whereypreandygtare the predicted value and groundtruth target,respectively.Mtestis the total number of the testing data.

It can be seen that the results tested with the groundtruth ESs have lower NMSEs than CNN and DNN methods,where the proposed graph construction and learning method can preserve the environment structure well.The results tested with the detected ESs are not that good compared with the ground-truth ESs because of the accumulated error of the ES detection,but they are still better than the CNN and DNN methods.Limited by the data,which only changes the environment in a specific space and the delay of paths is in a small range,the results of DS seem not that excellent and are sensitive to the scatterer detection error.

The CDFs are plotted in Figure 11,for a more intuitive illustration since the NMSE result can not represent the distribution,where the horizontal coordinate represents the parameter values,and the vertical coordinate is the cumulative probability.Identity with the NMSE results,we can figure out that the CDF plots of the ELSP with ground-truth ESs are more identified with that of ground-truth values compared with the other methods.As for the time cost,around 17 minutes and 0.0034s are required for training and one environment sample prediction,respectively.

5.4 SSP Prediction Results

Similar to the results of LSP,the NMSE and the CDFs of the results are utilized for performance evaluation.The number of graphs is more than the original quantity for that there might be more than one scatterer that brings about one order propagation,i.e.,5014 and 1065 samples of training and testing.Figure 12 illustrates the CDF plots of the power,delay,AOA,AOD,ZOA,and ZOD,respectively.For each parameter,the groud-truth values(gt),PSSP-gt(with the groundtruth PSs,PSSP (with the detected PSs),CNN (with the ground-truth PSs),and DNN (with the groundtruth PSs)are presented for performance comparison.We can acquire the same conclusion by getting the testing NMSEs of each parameter,as illustrated in Table 2.Similar to the LSP results,the model with the ground-truth PSs can obtain better performance than the corresponding CNN and DNN methods.Even the model with the detected PSs can outperform the nonstructure learning methods.Moreover,compared with the LSP prediction,the results of LSP have lower NMSEs because of the certain structure representation of the three nodes in the SC-PEGs.Moreover,the model can be trained within 18 minutes and takes around 0.0059s for each SSP prediction.

5.5 System Results

In order to evaluate the system performance,the channel capacity of multiple-input single-output (MISO)is simulated with the Eq.(2).Uniform planar arrays(UPA)with 4 antenna elements are applied.The data rate of the simulated channel can be calculated as

VI.CONCLUSION

The EICP method is proposed by leveraging the environment information directly,which consists of scatterer detection and scatterer detection-based channel prediction.The graph representation is constructed to reserve the structural information,and GNN-based models are employed to map the proposed environment graphs and the channel.According to the basic environment information,the target scatterers,LSP,and SSP can be predicted with low computational costs and get close results with ground-truth values.Moreover,compared with the learning methods of data in Euclidean space,the GNN trained with the graphs can outperform.However,as an initial work,there are certain limitations,and still,much effort could be made to meet the commendation of the 6G network.For example,based on the primary environment graph representation,how the representation can be refined for typical scenarios and whether other high-level representations can be defined to enhance scene generalization are the direction of our future improvement.

ACKNOWLEDGEMENT

This work was supported by the National Science Fund for Distinguished Young Scholars(No.61925102),National Natural Science Foundation of China (No.62101069),National Natural Science Foundation of China (No.62031019),National Natural Science Foundation of China (No.92167202),and BUPT-CMCC Joint Innovation Center.