UWB Channel Modeling and Simulation with Continuous Frequency Response

Kai Mao,Qiuming Zhu,Xijuan Ye,Ruirui Feng,Fuqiao Duan,Yang Miao,Maozhong Song

1 The Key Laboratory of Dynamic Cognitive System of Electromagnetic Spectrum Space,College of Electronic and Information Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China

2 The Radio Systems,Faculty of Electrical Engineering Computer Science and Mathematics(EEMCS),University of Twente,the Netherlands

Abstract: Ultra-wideband (UWB) technology is a prospective technology for high-rate transmission and accurate localization in the future communication systems.State-of-art channel modeling approaches usually divide the UWB channel into several sub-band channels and model them independently.By considering frequency-dependent channel parameters,a novel analytical UWB channel model with continuous frequency response is proposed.The composite effect of all frequency components within the UWB channel on the channel impulse response(CIR)of delay domain is derived based on the continuous channel transfer function(CTF)of frequency domain.On this basis,a closed-form simulation model for UWB channels and geometry-based parameter calculation method are developed,which can guarantee the continuity of channel characteristics on the frequency domain and greatly reduce the simulation complexity.Finally,the proposed method is applied to generate UWB channel with 2 GHz bandwidth at sub-6GHz and millimeter wave (mmWave) bands,respectively.The channel measurements are also carried out to validate the proposed method.The simulated CIR and power gain are shown to be in good agreement with the measurement data.Moreover,the comparison results of power gain and Doppler power spectral density(DPSD)show that the proposed UWB channel model achieves a good balance between the simulation accuracy and efficiency.

Keywords:ultra-wideband(UWB)channel; continuous frequency response;frequency-dependent channel parameters;simulation model;channel measurement

I.INTRODUCTION

In the fifth generation (5G) or sixth generation(6G)communication networks,the broader bandwidth would be adopted for high transmission rate especially in the millimeter wave(mmWave)communication systems [1,2].Different from the narrowband communications,the wideband communications especially the ultra-wideband (UWB) communications(normally with a large relative bandwidth 20% or a large absolute bandwidth 500 MHz [3]) would experience frequency-dependent channel characteristics within the broad bandwidths [4,5].Therefore,it is vital to propose an accurate channel model for the design,optimization,and evaluation of UWB communication systems.

So far,a lot of channel measurement campaigns for wideband or UWB communications have been reported in[6–10].These works mainly focused on analyzing the channel characteristics,i.e.,path loss,delay spread,power angular spectrum,and power delay profile (PDP) based on the measurement data.However,the channel modeling framework was not fully studied for generating the wideband or UWB channel.Some traditional wideband channel models can be found in [11–15].These channel models included more multi-path components than the narrowband channel due to the high delay resolution of wideband communication system.However,the wideband channel was modeled only with respect to the center frequency.Therefore,these channel models might not be applicable in UWB channel directly since they did not consider the frequency-dependent characteristics.Although the authors in[4,16]introduced frequencydependent parameters into the UWB channel models,these models still aimed at different specific frequencies.In other words,the composite effect of different frequency components within the bandwidth on the channel model was not studied.Recently,the authors in [5,17]proposed a UWB channel model by dividing the whole channel into several sub-band channels.These works provided a great scheme to describe the composite effect of different frequency components on the UWB channel.However,these models did not consider the effect of continuous frequency components on the channel characteristics.Moreover,it is normally difficult to determine the number of subband and is complicated to simulate the UWB channel by generating many sub-band channels.

This paper aims to fill up this gap.The novelties and contributions of the work are summarized as follows:

1) A novel UWB channel model with continuous frequency response is proposed,which involves the frequency-dependent channel parameters and composite effect of different frequency components.

2) A closed-form channel simulation model is derived for the first time to reduce the complexity of simulation by introducing the integral form instead of discrete sub-bands.

3)The simulated results of proposed UWB channel model,i.e.,channel impulse response (CIR),power gain,and Doppler power spectral density(DPSD)are validated by the channel measurement data and theoretical analysis at sub-6GHz band and mmWave band,respectively.

The rest paper is organized as follows.In Section II,a UWB theoretical channel model with continuous frequency response is proposed.The UWB simulation model is derived and the model parameters are calculated in Section III.In Section IV,the proposed UWB channel model is simulated and validated.The conclusion is drawn in Section V.

II.THEORETICAL CHANNEL MODEL

The UWB signal can be seen as the combination of infinite frequency components.It has been proved that different frequency component would experience different path delay,path loss,and path phase[9,18].For the traditional wideband channels,the effect of different frequency components on the channel parameters is limited because of narrow bandwidth,so the channel can be modeled only with respect to the center frequency.However,the channel properties of different frequency components could vary a lot within the bandwidth of UWB channel,which cannot be ignored.Considering the difference of frequency components on the path delay points is limited,it is assumed that different frequency component experiences the same path delay but has different path loss and path phase in this paper.

For an arbitrary single carrierf′ ∈[fL fH],the theoretical CIR with respect to frequency can be modeled as

whereα(t,τ;f′),ψ(t,τ;f′),andτ′are the amplitude gain,path phase,and delay of propagation path,respectively.By performing the Fourier transform in delay domain,we can obtain the channel transfer function(CTF)for the single carrier as

From the view of frequency domain,the UWB channel can be seen as the combination of infinite CTFs caused by different single carriers within bandwidth[fL fH],so the whole CTF can be expressed as

It should be mentioned that the path power gains of different frequency components are added together in(3),so the power gain should be divided by the bandwidth to obtain the average power gain for the whole UWB channel.

Finally,the proposed continuous frequencydependent CIR for UWB channels can be obtained by performing the inverse Fourier transform of CTF as

It can be found that the CIR of each path is the composite effect of different frequency components,which can be described by the frequency-dependent power gain,path delay,and path phase.The UWB channel modeling framework of this paper is shown in Figure 1.Note that this channel modeling framework can also be applied to the traditional narrow and wideband channels.

III.FREQUENCY CONTINUOUS CHANNEL SIMULATION

3.1 UWB Channel Simulation Method

In the realistic communication scenario,the distribution of scatterers is normally discrete.In other words,the path delays are not continuous.Thus,the theoretical UWB channel model of(4)can be rewritten as

whereNis the number of valid propagation paths,α(t,τn;f′),ψ(t,τn;f′) ,andτnare the amplitude gain,path phase,and path delay ofnth propagation path,respectively.For simplicity,α(t,τn;f′) andψ(t,τn;f′) are denoted asαn(t;f′)andψn(t;f′),respectively.It should be mentioned that the proposed model can be reduced to the traditional wide-band channel model [11,19]and multiple sub-band UWB (MSB-UWB) channel model [5,17].The traditional wide-band channel model can be expressed by changingf′into constant center frequencyfcas

On this basis,the MSB-UWB channel model can be viewed as the summation of several sub-band channels as

whereMis the number of sub-band channels andf′mis the center frequency of themth sub-band.It should be mentioned that the frequency response of MSB-UWB channel model is not continuous,which also consumes much more time to generate the channel.

It is hard to generate the UWB channel by directly using(5)due to the integral operation.Therefore,a key step is to calculate the expressions of frequency-dependent path gain and phase,and then obtain the closed-form channel model.In this paper,the amplitude gain is calculated as

wherecis the light speed,andξnis the scenario-dependent coefficient ofnth path.The path phase is modeled by two parts,i.e.,initial phase and the phase caused by Doppler frequency as

whereψ0is the random initial phase distributed uniformly over [0,2π),vT/R(t) and rT/Rn(t) are the velocity and spherical unit vectors of transceivers,respectively.The spherical unit vectors can be further expressed as

and

whereαTn(t) andβTn(t) are the azimuth angle of departure(AAoD)and the elevation angle of departure(EAoD),respectively,αRn(t)andβRn(t)are the azimuth angle of arrival(AAoA)and the elevation angle of arrival(EAoA),respectively[20].Note that Doppler frequency is an important channel parameter which becomes more complicated for the UWB case.For the narrow and wideband channel models,the Doppler frequency is non-frequency-dependent and determined by the velocity and center frequency.However,the deviation of Doppler frequency due to different frequency components is non-negligible for the UWB case.Taking a UWB channel with 2 GHz bandwidth and center frequency 28 GHz as an example,the relative velocity for a specific path is 100 m/s,so the theoretical Doppler frequency is 9333.3 Hz for the whole channel according to the traditional definition.However,if we consider the frequency factor in the proposed model,the theoretical Doppler frequency for this channel could range from 9000 Hz to 9666.7 Hz.

By substituting (8)–(9) to (5),the closed-form UWB channel model can be expressed as

wherevrelis denoted asvrel=Ei(·) is the exponential integral function.The exponential integral function can be expressed as Ei(x)=−e−t/tdt.In the exponential integral function,the velocity is in the denominator,so the channel model is divided into two cases for mathematical reason.The parameters used in (12) are also summarized in Table 1.Except for the user-defined parameters,the setups of other parameters are presented in the Section 3.2 and simulation part.Note that the UWB channel can be generated by(12)instead of generating and summating infinite sub-band channels,which would greatly reduce the complexity of simulation.

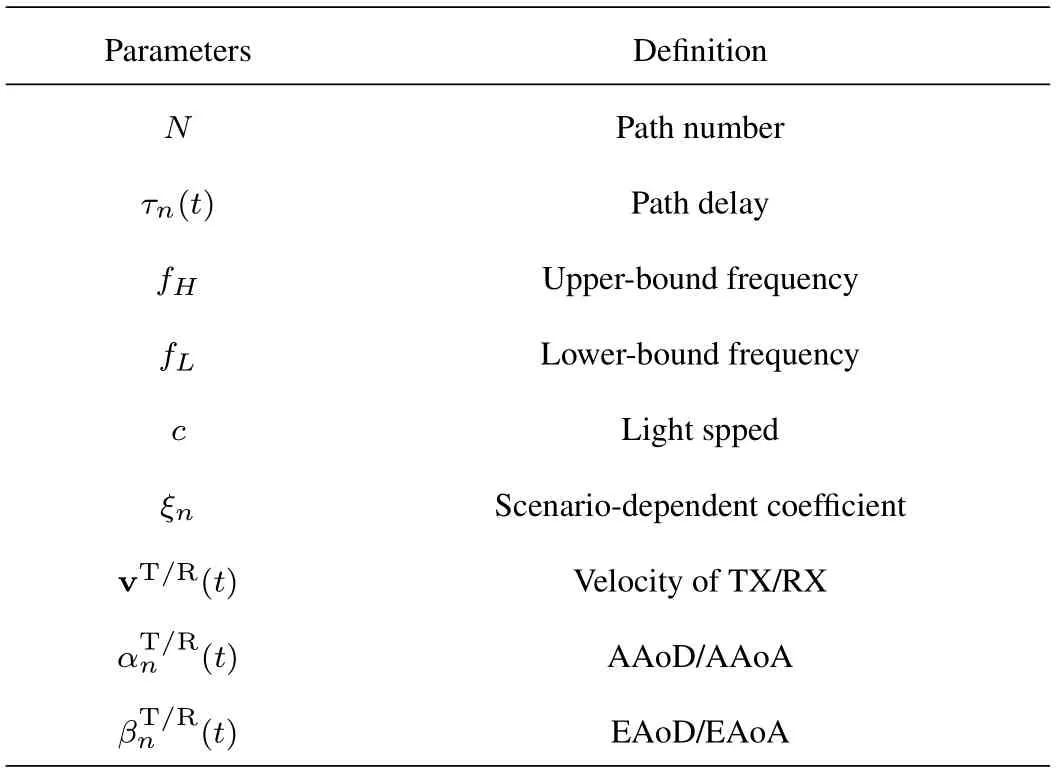
Table 1.Parameter definitions of proposed channel model.

3.2 Geometry-Based Parameter Calculation

The UWB channel model is parameterized by several parameters,i.e.,velocity,frequency range,delay,and angle.The velocity and frequency range are normally user-defined.The delay and angle parameters can be calculated in a deterministic way based on the geometric information.Assuming that the transceivers are moving in a three-dimensional trajectory,the velocity can be denoted as

wherevT/R(t),αT/Rv(t),andβT/Rv(t)are the magnitude,azimuth angle,and elevation angle of vT/R(t),respectively.Thus the location of transceiver can be expressed as

where LSn(t)is the location ofnth scatterer,which can be determined by the geometric information from digital map[21,22].The AAoD and EAoD of LoS and NLoS path can be calculated respectively by

where (·)xand (·)zare thexandzcomponent of vector,respectively,sT,LoSαandsT,NLoSαare the sign coefficients for LoS and NLoS path,respectively,which can be further expressed as and

Similarly,the AAoA and EAoA of LoS and NLoS path can be calculated respectively by

wheresR,LoSαandsR,NLoSαcan be expressed as

IV.SIMULATION RESULTS AND VALIDATIONS

For the proposed channel model,different frequency components have independent and composite effect on the power gain,Doppler frequency,and path phase of each path.Since the time-variant path phase is mainly determined by the Doppler frequency,this section focuses on analyzing and verifying the frequency-dependent power gain in a static scenario and Doppler frequency in a mobile scenario.We have also conducted field measurements at sub-6GHz and mmWave bands in a static indoor office scenario by using the vector network analyzer (Agilent VNA N5230A).The office room and transceivers’ setup are shown in Figure 2.There are rich scatterers in the room,i.e.,marble floor,wall,wooden desk,metal laboratory table,and air conditioner.The TX and RX are equipped with an omnidirectional antenna for sub-6GHz band and with a directional horn antenna for mmWave band.Note that the antenna power gain is also frequency dependent,so this factor is removed from the VNA measurement data in this paper.The sampling point of VNA is set as 2001,so the frequency interval for 2 GHz bandwidth is 1 MHz.And the sweeping bandwidth of VNA is set as 100 KHz.

For the sub-6GHz band,the center frequency is set as 3.5 GHz.In the static scenario,we can use(12)by settingvrel=0 to simulate the UWB channel.Note thatξnin the proposed channel model is fitted by the measurement data of indoor office scenario as 5,14,and 19 for the LoS path,single bounce,and double bounce of NLoS path,respectively.The measured CIRs can be obtained by performing the inverse Fourier transform of CTFs.To validate the correctness of proposed UWB channel model,we compared the simulated and measured CIR at the bandwidth of 2 GHz with LoS distance 3 m as shown in Figure 3.It can be found that the since our proposed UWB channel model is a ray-based one and the omni-directional antenna used in the VNA sounder is not isotropic,the CIR of proposed model shows more multi paths than that of VNA measurement.It should be mentioned that the CIR of proposed model can also be transformed into a cluster-based one like the CIR of VNA measurement by using the CIR reconstruction method in[23].Note that the bounce orders of NLoS paths can be obtained as well since the deterministic parameter calculation method is used in Section 3.2.For the NLoS paths,there are obvious two layers in Figure 3 for single and double bounce paths,respectively.There are some lower peaks in Figure 3 which could be the multi-bounce paths in higher orders.In the proposed channel model,we only consider the single and double bounce paths since the power gain of multi-bounce path in higher order is normally low.Anyway,the CIRs of proposed model and VNA measurement are showing good agreement in tendency and pattern.

Moreover,to demonstrate the composite effect of different frequency components on the channel parameters,the power gain of LoS path is simulated and measured with 2 GHz bandwidth at sub-6GHz band.For comparison purpose,the traditional wideband channel and the MSB-UWB channel model are also simulated under 2 GHz bandwidth based on (6) and (7),respectively.The number of subbands is set as 20.In the measurement,the LoS distance varies from 1 m to 4 m with the distance interval of 0.25 m.The LoS power gains of VNA measurement,proposed channel model,traditional wideband channel model,and MSB-UWB channel model are shown in Figure 4(a).To further analyze the performance of simulated results,the mean square errors between the measured results and the simulated results are calculated to evaluate the model accuracy,and the time consumptions of different models are recorded in a computer with Intel i5-8250U CPU and 16 GB RAM as well.It can be found that the mean-square error(MSE) of MSB-UWB channel model is really close to the one of proposed channel model.However,the MSB-UWB model takes about six times as long as the other models because it needs to generate multiple sub-band channels.For the traditional wideband model,it takes the shortest simulation time,but is with a poor performance.That is because the power gain varies a lot within 2 GHz bandwidth for the sub-6GHz band,and the composite power gain of different frequency components is higher than the one of center frequency.The proposed UWB channel model achieves a good balance between the accuracy and complexity.

Meanwhile,the same simulations and VNA measurements are performed at 28 GHz mmWave band.For the mmWave band,ξnof LoS path is 5 as well in this scenario.It should be mentioned thatξnof NLoS path for sub-6 GHz band maybe not applicable on the mmWave band anymore,whereξnshould be determined according to the corresponding measurement data.The measured CIR with horn antenna at the LoS distance of 3 m is shown in Figure 5(a).Since we focus on validating the composite effect of different frequency components on the parameters of LoS path,the horn antenna is used to measure the CIR.Therefore,the measured CIR mainly includes a strong LoS path.The LoS power gains of VNA measurement,proposed channel model,traditional wideband channel model,and MSB-UWB channel model are shown in Figure 5(b).Different from the results of sub-6 GHz band,the LoS power gains of all the channel models at mmWave band are really close to each other because the power gain does not change a lot within 2 GHz bandwidth for 28 GHz mmWave band.However,the conclusions of time consumption for different models are still the same as in Figure 4(b).It should be mentioned that the measured LoS power gains in both Figure 4 and Figure 5 are obtained by averaging five rounds of measured results to reduce the random error of filed measurement.

For the 28 GHz mmWave band,although the composite effect of different frequency components on the power gain is negligible,the effect on the Doppler frequency matters a lot.To demonstrate it,the Doppler frequency is analyzed under different bandwidth channels,i.e.,2 GHz,1 GHz,and 200 MHz in a mobile scenario.We can generate the channel via (12) withvrel≠0.The DPSD is adopted to observe the power distribution with respect to different Doppler frequencies.Since the effect of different frequency components on each path,i.e.,LoS path,ground reflection path,and other NLoS path are similar,we take the DPSD of LoS path as an example,which can be expressed as(24).

In the simulation,the TX is assumed to move to the RX along a straight line and constant velocity 100 m/s.When the distance of TX and RX comes to 7 m,the simulated DPSDs of LoS path with different bandwidths and the ones of traditional model are shown in Figure 6.It can be found that the Doppler frequency of traditional model is close to the theoretical value 9333.3 Hz.The Doppler frequency of our proposed channel model at the bandwidth of 2 GHz covers from 9002.69 Hz to 9667.21 Hz,which is well consistent with the theoretical one.Moreover,the theoretical power gain of LoS path for traditional model at the distance 7 m is about-83.241 dB,while the power density of traditional model is-82.89 dB/Hz since the width of simulated DPSD is close to 1 Hz.For the proposed channel model,the theoretical power gain of LoS path at the bandwidth 2 GHz is calculated as-83.245 dB.In Figure 6,the total power gain of LoS path at the bandwidth 2 GHz can be calculated asalso consistent with the theoretical one.Finally,we find that the range of Doppler frequency varies with different bandwidths.Therefore,it is not appropriate to model the wideband or UWB channel with traditional wideband model.which is

The DPSD of MSB-UWB channel model with 5,10,20,and 100 sub-bands are simulated under this scenario as shown in Figure 7.The range of Doppler frequency are well consistent between the proposed model and MSBUWB model.Moreover,the simulated DPSD of MSBUWB model is closer and closer to the theoretical one as the increase of sub-band number.Note that although the power gain of MSB-UWB model is already close to the proposed model with only 20 sub-bands,while the DPSD is still not accurate even with 100 sub-bands.Therefore,in order to obtain the approximate continuous frequency response,the MSB-UWB model needs to generate quantities of sub-band channels which would consume lots of simulation time.

V.CONCLUSION

This paper has proposed a novel UWB channel model with continuous frequency response,which takes into account of continuous frequency-dependent channel parameters,i.e.,power gain,Doppler frequency,and path phase.The composite effect of different frequency components has been modeled in an integral form for the first time.Then,a closed-form UWB channel model and simulation method have been derived.Simulated and measured results at different bandwidths have shown that the proposed method could improve the simulation accuracy and efficiency in comparison with the traditional wide-band or MSB-UWB channel models.In the future,we would carry out more field measurements under the mobile scenarios to validate Doppler frequency and further analyze other channel characteristic such as temporal and spatial channel correlations.

ACKNOWLEDGEMENT

This work was supported in part by the National Key Scientific Instrument and Equipment Development Project (No.61827801),in part by the National Natural Science Foundation of China (No.62271250),in part by Natural Science Foundation of Jiangsu Province (No.BK20211182),in part by the Key Technologies R&D Program of Jiangsu(Prospective and Key Technologies for Industry) under Grants BE2022067 and BE2022067-3,in part by China Scholarship Council,and in part by Postgraduate Research& Practice Innovation Program of Jiangsu Province,No.KYCX220360.