V2V Channel Modeling at 5.2 GHz for Highway Environment

Suying Jiang,Wei Wang,*,Ibrahim Rashdan

1 School of Information Engineering,Chang’an University,Xi’an 710064,China

2 Institute of Communications and Navigation,German Aerospace Center(DLR),Oberpfaffenhofen 82234,Germany

Abstract: To design and evaluate vehicle-to-vehicle(V2V) communication systems in intelligent transportation system (ITS),it is important to understand the propagation mechanisms and channel models of V2V channels.This paper aims to analyze the channel models at 5.2 GHz for the highway environment in obstructed line-of-sight (OLoS) and line-of-sight(LoS) scenarios,particularly the vehicle connectivity probability derivation based on the propagation model obtained from measurement.First,the path loss (PL),shadow fading (SF),narrowband K-factor,and small-scale amplitude fading are analyzed.Results showed that the received signal magnitude follows Rice and Weibull distribution in LoS and OLoS scenarios,respectively.Second,we develop simple and low-complexity tapped delay line (TDL) models with a 10 MHz bandwidth for LoS and OLoS scenarios;in addition,we investigate the wideband K-factor,the root mean square delay spread (RMS-DS),and delay-Doppler spectrum.Third,we derive the closed form connectivity probability between any two vehicles in the presence of Weibull fading channel,and analyze the effects of Weibull fading channel and traffic parameters on connectivity.It is found that Weibull fading parameter,transmit power and vehicle density have positive impact on connectivity probability,PL exponent has negative impact on connectivity probability.

Keywords: channel model; connectivity; highway;tapped delay line model;vehicle-to-vehicle

I.INTRODUCTION

The vehicle ad hoc network(VANET)is a type of ad hoc network that uses wireless communication to connect vehicles and other devices.It possesses multi-hop routing and dynamic topology characteristics,and is capable of facilitating information exchange between vehicles and systems in high-speed and high-density driving scenarios.The VANET is a critical component of the intelligent transportation system (ITS),which reduces traffic congestion,decreases accident rates,and improves transportation efficiency [1].VANETs can exchange information between vehicles,surrounding vehicles,pedestrians,and devices via vehicle-tovehicle(V2V)and vehicle to infrastructure(V2I)communication modes.Reliable V2V and V2I communication systems are required to enable the implementation of VANET diverse applications[2].V2V communication enables vehicles to exchange information between vehicles about accidents,weather,traffic,and roadblocks,etc.In this paper,we focus on V2V communications mode.

V2V communication systems have garnered considerable attentions in recent years due to their numerous applications,including increased road safety,efficient management of vehicle flow on the road,and reduction of traffic congestion [3].It is well established that developing an efficient and reliable V2V communication system requires a thorough understanding of the V2V channel characteristics and channel modeling [4–6].Due to V2V channels have the timefrequency selective fading nature,V2V channel is significantly different from the well-explored cellular channels[7–9].Numerous V2V channel measurement campaigns,channel models and characteristic analysis are required[10].

There are a lot of V2V channel measurement campaigns conducted in different scenarios,such as highway,rural,urban,tunnel,etc.Highway is a typical V2V scenario,it is of great significance to analyze the channel models and characteristics in highway environment.Several V2V measurement campaigns have been conducted in recent years,and channel models for the highway environment have been proposed.In previous studies,research on highway V2V channel modeling has primarily focused on statistical models,deterministic models,and geometry-based stochastic channel models (GSCMs).The statistical models include large-scale fading models (e.g.,path loss (PL)models [11–19]and shadowing models [20]),smallscale fading models(e.g.,amplitude fading,K-factor[21],root mean square delay spread(RMS-DS)models [22,23],delay-Doppler spectrum [24–27]),and tapped delay line(TDL)models[28],etc.In[20],authors analyzed shadowing effects.The normal distribution is found to be a good fit for the cumulative distribution function (CDF) of shadowing loss.In [21],the Rice distribution was used to model the envelope of the first delay bin.In [29,30],the amplitude fading of received signal was modeled,where Rice and Rayleigh distributions were used to describe the amplitude fading in line-of-sight(LoS)and Non-line-ofsight (NLoS) scenarios,respectively.TheK-factor and RMS-DS were calculated in[31],and it was discovered that theK-factor can be well described by a normal distribution,the CDF of RMS-DS can be well modeled by a lognormal distribution.The power delay profile (PDP),delay spread and Doppler spread were investigated in[32,33].In[34],the PL,RMS-DS,and angular spread were analyzed.These statistical models are simple and efficient in terms of computation.In[35],authors studied the relationship between K factor and distance in high-speed railway viaduct scenario,and established K factor model.In[36],authors evaluated the impact of large vehicle obstructions on the channel characteristics in terms of RMS-DS for both LoS and NLoS scenarios for a campus street environment.However,highway environment has not been considered.To our knowledge,most literatures focus on analysis of the channel characteristics in highway environment under LoS and NLoS conditions.The obstructed-line-of-sight (OLoS) scenario is a typical transportation scenario in reality and different from either LoS or NLoS scenario.The channel characteristics in the OLoS scenario are different from those in the LoS and NLoS scenarios.However,the researches on the channel characteristics for the highway in OLoS scenarios are few.

Additionally,several GSCMs and deterministic models have been proposed.In[4],authors developed a generic channel model based on geometry-based stochastic channel model(GSCM)that considers three distinct types of point scatterers,namely,mobile discrete scatterers,static discrete scatterers,and diffuse scatterers.The authors proposed a three-dimensional(3D) geometrical model for a wideband multipleinput multiple-output (MIMO) mobile to mobile fading channel in [37,38].In addition,the corresponding space-time-frequency correlation function,power space-delay spectrum,and space-doppler power spectral density were derived for a 3D non-isotropic scattering scenario.Moreover,authors validated the proposed model using the measured data in[39].Thereafter,authors extended the model presented in [38]to include moving scatterers,and proposed a 3D geometrical propagation model in [40],which includes both moving and stationary scatterers around the transmitter (Tx) and receiver (Rx).These GSCMs are in good agreement with the real world.However,these models are computationally complex.In[34],authors modeled V2V millimeter wave (mmWave) channels using the ray-launching method,and then,calculated channel parameters,such as PL,RMS-DS,and angular spread.The accuracy of a ray tracing (RT) model is determined by the accuracy of the object database,and the more detailed the database,the more accurate the model is.However,because the real environment is usually more complex,it is difficult to accurately predict the reflection and diffraction rays.

It is well known that successful V2V communication depends on vehicle connectivity.Connectivity is a crucial performance metric for V2V communication.Communication channel characteristics have significant impact on the connectivity of VANET.For the highway environment,Weibull diatribution has been widely used to fit V2V fading channel.However,the connectivity analysis considering Weibull fading channel is not enough.In [41],authors presented the Weibull fading distribution,but V2V connectivity was not analyzed.In[42],authors considered that the inter-vehicle distance follows an exponential distribution,the speed of vehicle follows truncated Gaussian distribution,and used an equivalentM/G/∞queue for the connectivity analysis in one-dimensional VANET.In addition,Rayleigh,Rice,Weibull fading and log-normal shadow fading were considered in the paper.In [43],the system model used for connectivity analysis,which includes vehicle mobility models and fading models,is similar to the models used in[42].Moreover,the connectivity probability between two consecutive vehicles was derived.The connectivity probability between any two vehicles was not considered.However,in practice,two vehicles are often blocked by other vehicles,and the channel fading is different when the vehicles are blocked,so the vehicle connectivity is also different.In this case,the research on the connectivity probability between any two vehicle is important for VANET connectivity analysis.Therefore,in OLoS and NLoS scenarios,it is valuable to study the connectivity between any two vehicle.However,there are not so many researches focusing on OLoS condition that becomes a very interesting scenario for study of vehicle network connectivity.

To the best of our knowledge,the channel models and characteristics in OLoS scenario are not thoroughly studied,in addition,the connectivity probability between any two vehicles under Weibull fading channel is rarely studied.Therefore,in this paper,we focus on narrowband channel models,wideband channel models and connectivity model for the highway environment in LoS and OLoS scenarios.Especially,we derive the closed form connectivity probability between any two vehicles based on the propagation model obtained from measurement,which has not been given in literature; in addition,we propose simple and low-complexity traditional TDL models with a 10 MHz bandwidth for the highway in LoS and OLoS scenarios.The main contributions of this paper are summarized as follows:

(1) Together with the recorded video during the measurement,the measured channel impulse response(CIR) data are divided into two sets: LoS and OLoS scenarios.The magnitude of received signal in the highway is analyzed,and the results show that the magnitude of received signal follows the Weibull distribution in OLoS scenario.Based on the findings and proposed model,we derive the closed form connectivity probability between any two vehicles under Weibull fading channel; analyze the impacts of channel dependent parameters and traffic parameter on connectivity probability.

(2) Development of a wideband channel model for LoS and OLoS scenarios in a highway environment.We present a TDL multipath channel model including the small scale fading characteristics of individual taps,considering a typical vehicle communication bandwidth of 10 MHz.

(3)Development of a narrowband channel model in LoS and OLoS scenarios.Analysis of the PL,SF,andK-factors.

The remainder of the paper is organized as follows:Section II describes the channel measurement campaign.The narrowband channel models are discussed in Section III,emphasizing the path loss model,the shadow fading distribution,the distribution of normalized signal magnitude,and the narrowbandK-factor.Section IV presents some wideband channel model,specifically,TDL models,widebandK-factor,RMSDS,and delay-Doppler spectrum.Section V proposes the closed form connectivity model under Weibull fading channel,and studies the influences of different parameters on connectivity probability.Finally,the conclusions are given in Section VI.

II.MEASUREMENTS

To analyze the large-scale,small-scale channel characteristics,and to establish channel models for the highway,a V2V channel measurement campaign was conducted in Germany using the Medav RUSK-DLR broadband channel sounder.In this measurement campaign,the measurement type is single-input singleoutput(SISO).The Tx transmitted an orthogonal frequency division multiplexing (OFDM) signal at the center carrier frequency of 5.2 GHz with a measurement bandwidth 120 MHz.The Rx received the channel frequency response(CFR)and saved it in the hard disk.We can obtain complex CIR by inverse Fourier transform of the CFR.The delay resolutionτ∆isτ∆=,whereBdenotes bandwidth.The parameters of the channel measurement campaign are summarized in Table 1.

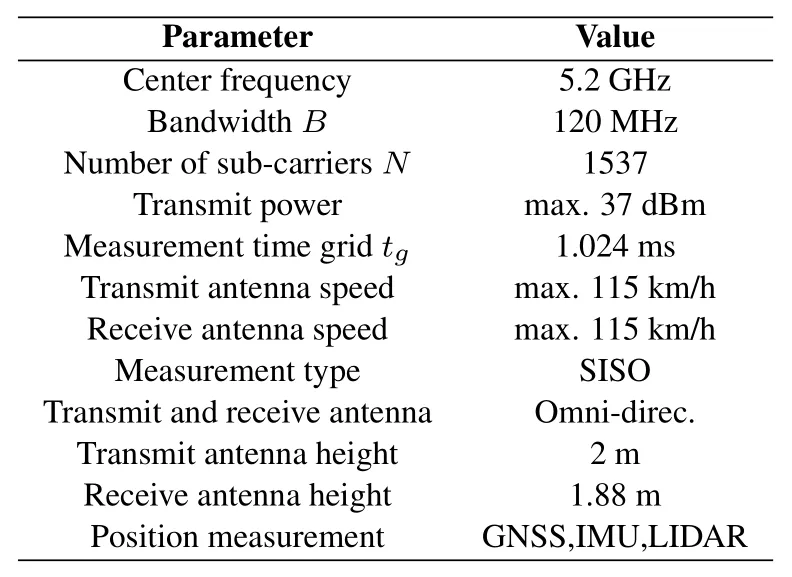
Table 1.Channel measurement parameters.

During the measurement,the Rx and Tx were in two cars,the receive antenna and transmit antenna were located on the roof of two cars.Two rubidium atomic clocks were used on each side to achieve time synchronization between Tx and Rx.In order to obtain the antenna positions at each instant of the measured CFR,the Global Navigation Satellite System (GNSS) receivers were used on the Rx and Tx sides.The GNSS receivers acquired signals from various satellite systems,including the Galileo system,the GNSS,and the Global Positioning System (GPS),etc.The positions of the antennas can be determined by post-processing the measured data.Additionally,the attitudes of the two cars were measured by the inertial measurement unit(IMU)on each side.The IMU data obtained from the GNSS receiver was time stamped with GPS time.The IMU data can be synchronized with the measured CFR and CIR.

Two cars traveled in the same direction on the highway during the measurement,moreover,the cars traveled at varying speeds and separations depending on the road traffic density.There are different scenarios that occur between Tx and Rx.The LoS is the situation in which there is an optical LoS between the receive and transmit antennas.The OLoS is the situation where the direct LoS between the receive and the transmit antennas is obstructed by another small vehicles.The NLoS occurs when buildings or vehicles with large size completely block the LoS path between the receive and transmit antennas.Using the video we recorded from the vehicle carrying Tx,we classified the measured data into LoS and OLoS categories.During this measurement,NLoS category is not found.As a result,in this paper,we focus exclusively on the channel characteristics and models in LoS and OLoS scenarios.Figure 1 depicts an LoS scenario on a highway,with the receiver traveling in front and the transmitter following behind.Figure 2 visualizes an OLoS scenario on a highway,where the LoS path between Tx and Rx is obstructed by a vehicle.The receiver is in front of the obstructed vehicle,the transmitter is behind the obstructed vehicle.Figure 3 illustrates the received power and the distance between Tx and Rx during the measurement.

III.NARROWBAND CHANNEL MODEL

3.1 The Path Loss Model

3.1.1 The Log-Distance Path Loss Model

The log-distance path loss model is widely used to characterize the radio propagation environment,which can be written as[44]:

whereddenotes the transmission distance in meters,PL(d) is the path loss at distanced(in dB).d0is the physical reference distance,we setd0is 1 meter.P0represents the reference path loss at the distanced0,nbeing the path loss exponent.Xσrepresents the largescale shadow fading,it is a zero-mean Gaussian distributed random variable(in dB)with standard deviationσ(in dB).

3.1.2 The Two-Ray Path Loss Model

In LoS cases,the path loss can be well modeled using a two-ray ground reflection model [12].This model takes into account the LoS path and a single reflected path from the ground surface.In the two-ray ground reflection model,the first Fresnel zone touches the ground at the break pointdbr=whereλdenotes the wavelength of the radio signal,hTandhRare the antenna heights of transmitter and receiver,respectively.In this measurement campaign,the critical distance is arounddbr=260 meters.The distance between Tx and Rx is frequently less than the break pointdbr.As a result,the reflected path originates primarily from the front of the transmitter car not from the ground.Therefore,in this paper,we will consider a two-ray model,including two rays,namely,the LoS path and a single reflected path from the Tx car,as illustrated in Figure 4.

In the two-ray model,the received power can be written as[45]:

whereλis the wavelength of the radio signal,Ptis the transmitted power,denotes the product of antenna field patterns along the LoS direction,denotes the product of antenna field patterns along the reflected path.dldenotes the propagation distance for the LoS path,drdenotes the propagation distance of the reflected path from the hood of the transmitter car,dlanddrare given by:

wheredis the distance between transmitter and receiver,hcis the height of the transmitter car hood.In Eq.(2),ϕis the phase difference between the LoS path and reflected path,it is written as:

In Eq.(2),Ris reflection coefficient of the reflected path,it is given by:

whereεis the relative complex permittivity of the vehicle,s=or 1 for the vertical or horizontal polarization.θis the incident angle.

3.1.3 Results and Discussion

For calculating the path loss,firstly,we should remove the effects of small-scale fading.The effect of small-scale fading is removed by averaging the received power over a sample time corresponding to a Tx movement of 30 wavelengths.The measured path loss and the empirical path loss models for LoS and OLoS scenarios are illustrated in Figure 5 and Figure 6,respectively.

Table 2 presents the path loss model parameters.It is demonstrated that large path loss exponents correspond to smallP0values,which is consistent with the results in[14].The path loss exponent in highway scenarios is 1.7616 in LoS case,and 2.1755 in OLoS case.The path loss exponent is greater in the OLoS scenario than in the LoS scenario.This is because some paths are blocked in OLoS scenario,resulting in lower received power and increased path loss compared to LoS scenario.

Table 2.Path loss model parameters.

3.2 Amplitude Distribution of Shadow Fading

The SF is caused by obstacles in the propagation path between the Tx and the Rx.Understanding the characteristics of SF is critical for designing of diversity and handover schemes [46].In this paper,the SF component is calculated under the assumption that the path loss model is a single-slope log-distance path loss model.

Figure 7 and Figure 8 illustrate the probability density functions(PDFs)of SF in LoS and OLoS scenarios,respectively.The results indicate that the measured SF(in dB)can be well fitted by the normal distribution.The standard deviations of SF are given in Table 2.

Table 3.The GoF values of different distributions.

3.3 Narrowband K-Factor

TheKfactor is a channel characteristic parameter that describes the small-scale fading channel characteristics.In this paper,we employ a simple momentbased method to estimate the K-factor,it is written as[47,48]

whereγis

wherexis the signal magnitude,V ardenotes the variance,Edenotes the expectation.

Before estimatingK-factor,the effect of the largescale fading should be removed.We removed the large-scale fading by using a moving average window of 80 wavelengths.The window size used to eliminate large-scale fading is greater than the window size used to calculate theK-factor.

We analyze the narrowbandK-factor for the highway environment in this subsection.Figure 9 shows theK-factor against the distance between transmitter and receiver.It is demonstrated that theK-factor decreases with increasing distance in LoS scenario.In OLoS scenario,K-factor also decreases with increasing distance,but not significantly.In Figure 9,the red and black lines represent the least square fitting lines for theK-factor in LoS and OLoS scenarios,respectively.The obtained linear model of theK-factor is written as:

whereddenotes the distance between transmitter and receiver.

3.4 Magnitude Distribution

In this paper,we fit the magnitude of the measured data to various distributions,specifically,the Rice,Weibull,Rayleigh,and Nakagami distributions.Before fitting the magnitude,we remove the influence of large-scale fading.In addition,the Kolmogorov-Smirnov(KS)test is used to assess the goodness of fit(GoF)of various distributions to the measured data.In this paper,we applied the KS test at a 5% significant level.In the KS test,the GoF valueρcan be written asstands for the supremum operator,F(x)andFX(x)denote the theoretical and empirical cumulative distribution functions(CDFs) of the measurement datax,respectively.A lowerρindicates a better fit for the model.

Table 3 lists the GoF values for different distributions.It is observed that Rice distribution has the lowestρin LoS scenario.Therefore,Rice distribution has the best fit for LoS scenario on the highway.Weibull distribution has the lowestρin OLoS scenario,and it has the best fit for OLoS scenario on the highway.

IV.WIDEBAND CHANNEL MODEL

4.1 Tapped Delay Line Model

According to the provisions of IEEE 802.11p,the bandwidth of 10 MHz is used for V2V applications[28].Therefore,the establishment of 10 MHz channel model is very important,and the establishment of accurate TDL model is helpful to the design of V2V communication systems.In this paper,we present TDL models for a 10 MHz bandwidth.The CIR of the TDL model can be written as[49]:

wheretdenotes time,Mdenotes the number of taps,ustands for the index of taps.αudenotes the timedependent complex coefficients for theu-th tap,τuis the delay for theu-th tap.

In order to obtain TDL model parameters,first,we fit the distribution of the amplitude for individual taps based on the measured data in a highway environment.Additionally,the KS test is used as the GoF indicator of different distributions.In this paper,four distributions are considered within the KS test,specifically,the Rayleigh,Rice,Weibull,and Nakagami distributions.

Table 4 and Table 5 summarize the GoF values of various distributions for each tap in LoS and OLoS scenarios,respectively.In Table 4,it is observed that the Rice distribution fits best to the empirical distribution of the amplitude for the first tap in LoS scenario;the Rayleigh distribution best fits the amplitude for the second tap in LoS scenario;the Weibull distribution has the best fit for the amplitude of remaining taps in LoS scenario.According to Table 5,the Rice distribution fits best to the empirical distribution for the amplitude of the first tap in OLoS scenario; the Weibull distribution has the best fit for the amplitude of the other taps.Therefore,the Weibull distribution provides a better description for a large number of taps in the highway environment.

Table 6 and Table 7 present the TDL model parameters in LoS and OLoS scenarios,respectively.It is shown that the first tap has much greater power than the other taps.Additionally,the shape parameter of Weibull distribution for the first tap is greater than two,indicating that the magnitude of the first tap follows the Rice distribution.In LoS scenario,the shape parameter for the remaining taps is close to two,indicating that the magnitude of other taps may be fitting well to the Rayleigh distribution.In OLoS scenario,the shape parameter for several taps is less than two,indicating that the fading of these taps worse than Rayleigh distribution.

4.2 Wideband K-Factor

An accurate characterization ofK-factor is necessary for channel modeling and communication system design.The narrowbandK-factor has been extensively studied in a variety of publications.It applies to GSCM and system simulations.The widebandKfactor can be used to develop a cluster delay line model or a TDL model[50].Both the narrowband and widebandK-factors are critical for channel modeling.In order to provide a reference for V2V communication system design,we estimate the widebandK-factor for a 10 MHz bandwidth.The widebandK-factors of the first two taps in different scenarios are calculated.

Table 8 lists the widebandK-factor parameters.The mean values ofK-factor for the first and second taps in the LoS scenario are 16.06 dB and 2.8 dB,respectively.The mean values ofK-factor for the first and second taps in the OLoS scenario are 11.86 dB and 1.32 dB,respectively.In general,theK-factor is larger in LoS scenario than in OLoS scenario for the same environment.This is due to the strong LoS component is obstructed in OLoS scenario.

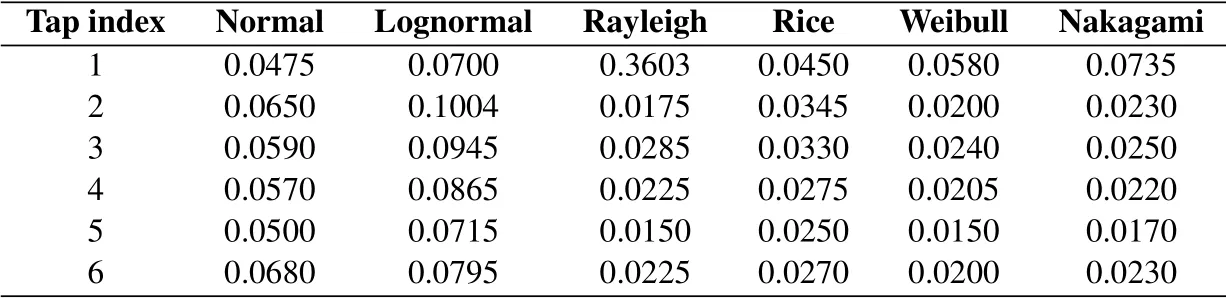
Table 4.The GoF values of various distributions for different taps in LoS scenario.

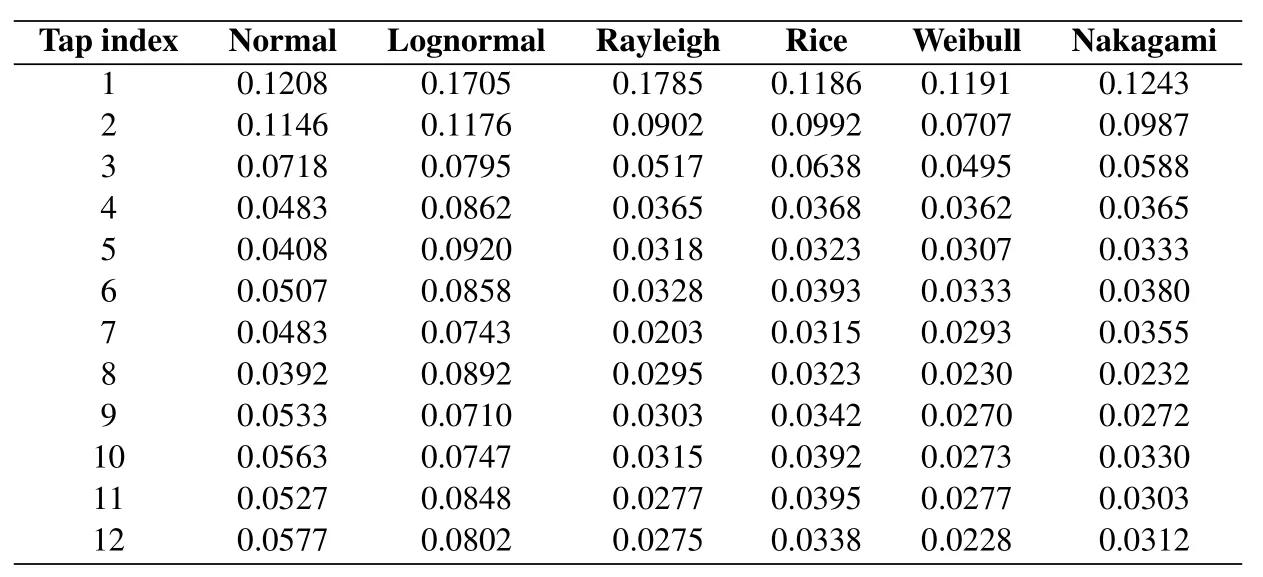
Table 5.The GoF values of various distributions for different taps in OLoS scenario.

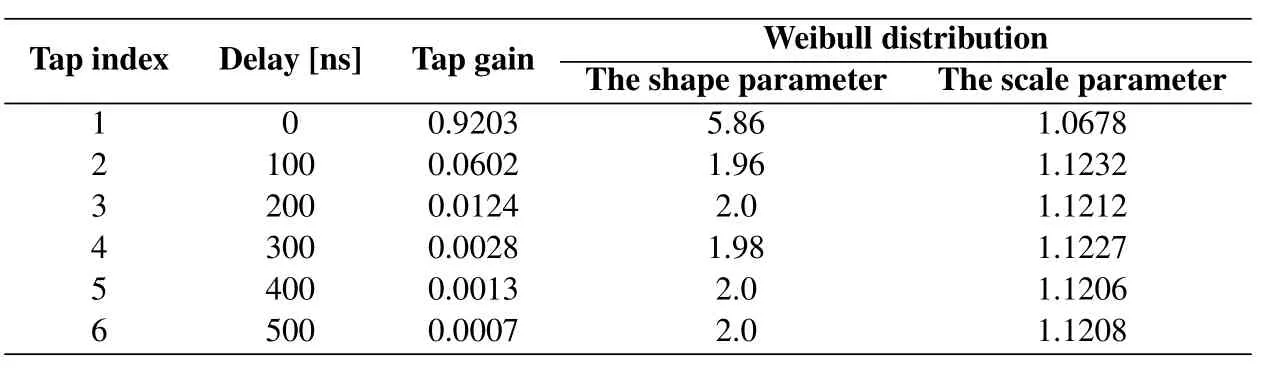
Table 6.The TDL parameters in LoS scenario.

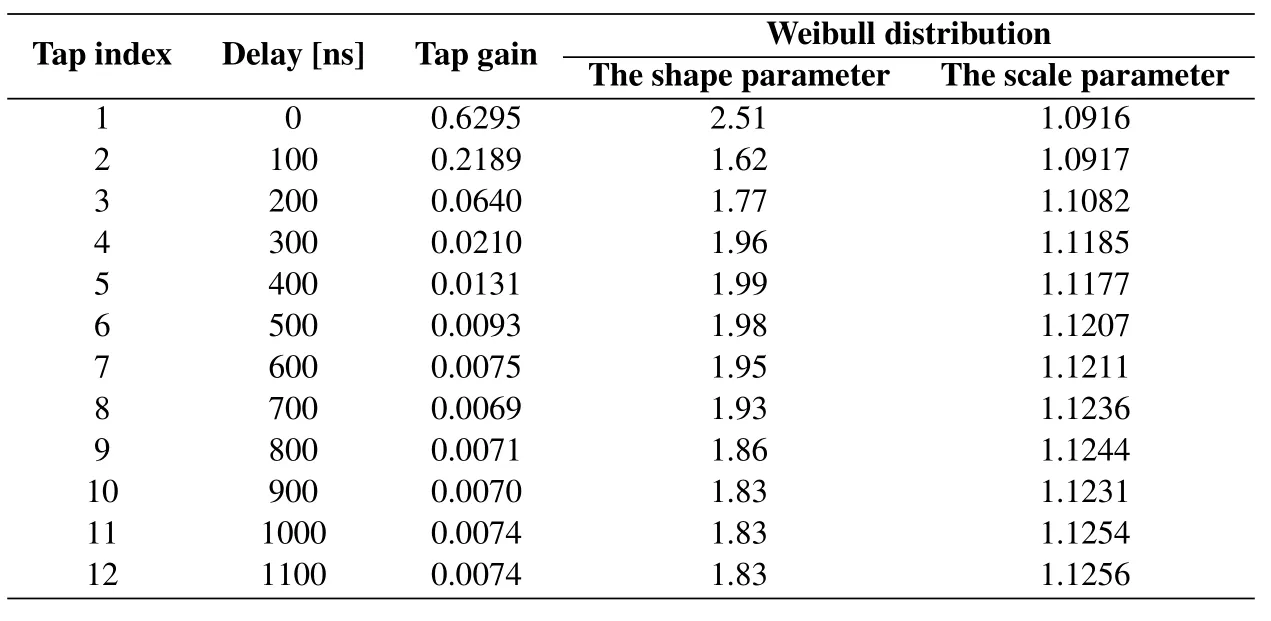
Table 7.The TDL parameters in OLoS scenario.

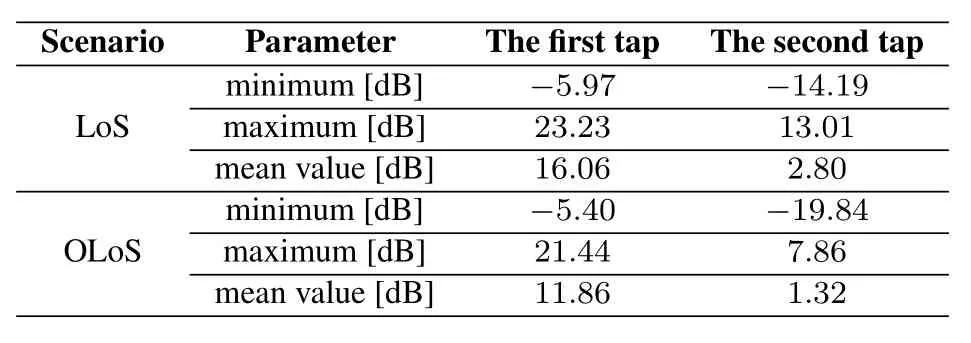
Table 8.K-factor results in LoS and OLoS scenarios.

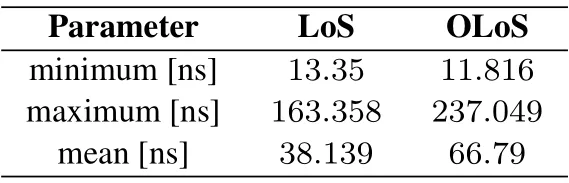
Table 9.RMS-DS parameters.

Figure 10 shows the CDF of theK-factor for the first two taps in LoS and OLoS scenarios.TheKfactor of the first tap is greater than the second tap.In addition,theK-factor is greater in the LoS scenario than in the OLoS scenario.

4.3 RMS-DS

The RMS-DS describes the temporal dispersion of the PDP,it is written as:

whereτidenotes the delay of thei-th path,P(τi)denotes the averaged PDP over a window length of 50λwith wavelengthλ;Dis the mean excess delay of PDP,it is determined as:

and Γ(y)stands for a threshold function defined as:

In this work,we choseytto be 13 dB above the noise level for each averaged PDPP(τi).Then,based on the measured data,we calculate the RMS-DS in different scenarios.

Figure 11 shows the empirical CDF of the calculated RMS-DS and the corresponding Lognormal distribution fitted model for LoS and OLoS environments.It is shown that the CDF of RMS-DS can be well modeled by Lognormal distribution.The CDF of RMS-DS reaches 1 at about 163 ns in LoS scenario.The CDF of RMS-DS reaches 1 at about 237 ns in OLoS scenario.In general,the RMS-DS in OLoS scenario is larger than in LoS scenario.The statistical parameters of RMS-DS are listed in Table 9.In LoS and OLoS scenarios,the mean values of RMS-DS are 38.139 ns and 66.79 ns,respectively.

4.4 Delay-Doppler Spectrum

In order to calculate the delay-Doppler spectrum,firstly,we need to divide the measured CIR snapshots into segments.Every segment includes snapshots within a time duration ofQt.It is noted that the time periodQtshould not be too large or too small.Qtshould be large such that the snapshots withinQtcan be used to obtain a high resolution of the Doppler spectrum.The time periodQtshould be small that the channel withinQtcan be seen as channel stationary,and the Doppler does not change significantly[51].In this paper,we usedQt=0.5 s.The delay-Doppler spectrum of thel-th segment can be obtained by taking the Fourier transform of snapshots within thel-th segment in the time domain.It can calculated as:

whereSl(v,τi)represents the delay-Doppler spectrum of thel-th segment,vdenotes the Doppler frequency,H(l,τi)denotes the snapshots within thel-th segment,H(l,τi)=[h(tkl,τi),··· ,h(tkl+1−1,τi)],whereklis the time index of the measured CIR snapshot of thelth segment.TheFt(·) stands for the discrete Fourier transform with respect to the variablet.

The Doppler spectrum of the LoS path can be calculated from the delay-Doppler spectrum at the LoS delay.It can be calculated as:

whereSl(v,τ0) is the delay-Doppler spectrum of the LoS path for thel-th segment,τ0=

We calculated the Doppler spectrum of the LoS path over the measurement time from the 57 s to 157 s.Figure 12 depicts the Doppler spectrum of LoS path.When the two vehicles were moving forward,the Doppler spectrum varied due to the changing attitude and speed of the transmitting and receiving vehicles.

V.CONNECTIVITY MODEL

In Section 3.4,simulation results showed that the received signal magnitude follows Weibull distribution in OLoS scenario.To the best of our knowledge,the research on connectivity between any two vehicle in the presence of Weibull fading channel is rare.In addition,the closed form connectivity probability between any two vehicles in the presence of Weibull channel is not given.In this paper,we derive the closed form connectivity probability considering both vehicle mobility and Weibull fading; in addition,we analyze the effects of different parameters on connectivity performance.

5.1 Traffic Modeling

We consider a single lane road with a lengthLkm.The number of vehicles passing the observation point per unit time follows Poisson distribution with rateλvehicles/h.Hence,the arrival time of consecutive vehicles follows an exponential distribution with the parameterλ.The distance between two adjacent vehicles is defined as adjacent vehicle distance,which follows an exponential distribution with the average vehicle densityρ.In order to distinguish the distance between two consecutive vehicles and the distance between any two vehicles,we defined the distance between any vehicles as inter-vehicle distance.The distance betweeni-th vehicle and(i+1)-th vehicle is a random variableXi,the PDF of adjacent vehicle distanceXiis written as:

In free flow state,the speed of vehicles is usually assumed to be a random variable following a Gaussian distribution.In this paper,in order to avoid dealing with negative speeds or speeds close to zero,we consider the speed of vehicle follows the truncated Gaussian PDF,which is given by[52]:

whereerf(·)denotes the error function,vmaxandvminare the upper and lower bounds of the vehicle speeds,respectively.f(v) is the Gaussian PDF,it can be defined as:

whereµvdenotes the average speed,σvis the standard deviation of vehicle speed.We setvmin=µv−3σv,vmax=µv+3σv.

In general,the inter-vehicle distanceZqbetween one vehicle and itsq-th neighbor can be defined as a sum ofqindependent and exponentially distributed adjacent vehicle distancesXiwithi=1,2,...,q.Therefore,Zqcan be represented byThe PDF of theq-th neighboring vehicle with a certain inter-vehicle distancexcan be written as follows:

where (·)! denotes the factorial operator,ρstands for the average vehicle density.

5.2 Weibull Fading Channel

The PDF of the received maginitudewin Weibull fading channel is given by:

wherearepresents the scale parameter,brepresents the shape parameter.We setC=b/a,whena=1,Eq.(20)can be written as[53]:

whereCrepresents the Weibull fading parameter,which controls the severity of channel fading.IfCis equal to 2,the distribution is equivalent to the Rayleigh distribution.WhenCis larger than 2,the distribution analogous to Rice distribution,represents the environments with LoS components.IfCis less than 2,the distribution represents the scenarios with significant NLoS components;in this cases,the fading worse than Rayleigh fading.

The PDF of the signal to noise ratio (SNR) in Weibull fading channel can be calculated as[53]:

where Γ(·)denotes the Gamma function;γis the SNR at a diatancedaway from the Tx,is the average SNR at a diatancedaway from the Tx[43],

5.3 Connectivity in Weibull Fading Channel

When the SNR of received signal is larger than the SNR threshold Ψ,the communication link is regarded as connected.The probability of correctly receiving transmitted data at the distancedis given by[43]:

wherendenotes path loss exponent,Pnoisedenotes the total additive noise power,it be calculated byPnoise=KbTB,whereKb=1.38∗10(−23)J/K is the Boltzmann constant,Brepresents the bandwidth,Tdenotes temperature in K; Ψ denotes the SNR threshold;PTis the transmit power,ddenote the distance between receiver and transmitter;β=GTGRc2/(4πfo)2is a constant value,it is associated with path loss model,whereGTandGRare the transmit antenna gain and receive antenna gain,respectively.During the measurement,we used omni-directional antennas,therefore,GT=1,andGR=1;fodenotes the carrier frequency,cis the speed of light.

From Eq.(19) and Eq.(22),the joint PDF of the inter-vehicle distance and the SNR is given by:

The single-link connectivity probability of the vehicle and itsq-th neighbor can be derived as Eq.(25).Whenq=1,Eq.(25)is the connectivity probability for consecutive vehicles.

In order to evaluate the integral in Eq.(25),we consider the derivation as in[54],then the integral can be written as:

wheres,u,andtare larger than 0.In addition,it is worth mentioning that Eq.(26) is valid for positive integer values ofbandis the Meijers G function.Ifis a positive integer,the integral in Eq.(25)can be written in terms of Meijer’s G function.By substituting Eq.(26) into Eq.(25),Eq.(25) can be re-written as Eq.(27).

wherePnoisedenotes the total additive noise power,Cis the Weibull fading parameter;qis the neighbor order,it representsq-th neighboring vehicle of the target vehicle;Wis given by:

wherenis path loss exponent,χcan be calculated as:

For integer of 2/C,Γ(1+2/C)=(2/C)!,therefore,Eq.(27) can be written as Eq.(30).Eq.(30)is the closed form connectivity between any two vehicles.

where

5.4 Simulation Results

In the following,we present the numerical simulation results of the influence of different parameters including the Weibull fading parameterC,neighbor order,transmit power,path loss exponent,and vehicle density on connectivity probability.

The simulation parameters are set as:n=2.2,the transmit powerPT=37 dBm,Pnoise=−90 dBm,the SNR threshold Ψ=30 dB,the average vehicle densityρ=0.03 vehicles/m,the constant valueβ=2.1∗10(−5).Figure 13 illustrates the effect of parameterCon connectivity performance for consecutive vehicles.Results showed that the connectivity probability increases whenCincreases.It can be also explained by the fact that increasingCimplies the presence of strong dominant components,which indicates smaller variation in power caused by small scale fading.Thus,the connectivity probability is increased.

Figure 14 shows the variation of single-link connectivity probability versus neighbors orderqunder Weibull fading.It is shown that the close neighbors have higher connectivity probability than the farther neighbors.

The V2V connectivity performance is related to transmit power and the setting of threshold values parameters.The effects of transmit power on consecutive vehicles connectivity probability are shown in Figure 15.Results showed that the connectivity probability increases as transmit power increases.

The effects of path loss exponentnand vehicle densityρon consecutive vehicles connectivity probability are shown in Figure 16 and Figure 17,respectively.We set path loss exponentnis range from 0.5 to 10,ρis range from 0.001 to 0.1.Results showed that with path loss exponent increases,the connectivity probability decreases.As expected,the path loss exponent can decrease the connectivity probability of a VANET;in the free traffic flow,with the vehicle density increases,connectivity performance increases.

VI.CONCLUSION

The focus of this paper is to analyze the modeling and characteristics of V2V channels in a highway scenario.First,we described the channel measurement campaign in detail.Then,using the measured data,we established narrowband channel models for the highway,including PL model,SF model,small scale amplitude fading model,and narrowbandK-factor model.It is found that theK-factor is dependent on the distance between the Tx and Rx; in LoS and OLoS scenarios,theK-factor decreases as the distance between Tx and Rx increases.In addition,the Rice distribution has the best fit for signal magnitude distribution in LoS case,the Weibull distribution fits signal magnitude distribution best in OLoS case.

Second,we established several wideband channel models,specifically,the TDL model,the widebandK-factor model,and the RMS-DS,etc.In this paper,we presented TDL models for a 10 MHz bandwidth in LoS and OLoS scenarios that can be used for VANET V2V communication.Additionally,the results indicate that theK-factor of the first tap is greater than theK-factor of the second tap; and theK-factor in LoS scenarios is greater than theK-factor in OLoS scenario.In OLoS scenario,the RMS-DS is greater than in LoS scenario.In LoS and OLoS scenarios,the CDFs of RMS-DS follow a Lognormal distribuiton.

Third,we derived the closed form connectivity between any two vehicles under Weibull fading channel for the cases of integernC/2 and 2/C;in addition,we analyze the impacts of channel dependent parameters(i.e.,Weibull factor,neighbor order,path loss exponent,transmit power.) and vehicle density on connectivity probability.The shape factor of Weibull fading parameter have positive impact on connectivity performance.The larger neighbor order,the smaller connectivity probability.Furthermore,it is found that path loss exponent has negative impacts on connectivity probability,transmit power has positive impact on the connectivity probability.In free traffic flow,high vehicle density results in an increased connectivity probability.The V2V channel modeling is extremely beneficial for the design and performance analysis of V2V communications.The channel models presented in this paper enable provide some reference for the applications of V2V communication technology in ITS.

In V2V channel,the transmitter and receiver move rapidly,which leads to the fast varying channel.The high dynamics of underlying propagation environment causes significant channel spatial-temporal non-stationarity [6].Therefore,channel time nonstationarity is a typical channel characteristic for V2V channel.However,we focus on short term channel non-stationarity in the paper.In the future,we will study fading characteristics and cross-correlation characteristics of multipath components in time-delay domain of TDL model for non-stationary channels.Further,we will focus on appropriate time evolution model among adjacent CIRs.Another future work is applying super-resolution channel parameters tracking algorithm to track the multipath components in order to analyze and model the reflection and scattering paths from surrounding vehicles and other objects.

ACKNOWLEDGEMENT

This work was supported by the National Natural Science Foundation of China (No.61871059),and Scientific Innovation Practice Project of Postgraduates of Chang’an University(No.300103722006).