让学生品味“数学味” 让课堂彰显“数学化”
——“数学归纳法”教学实录与反思*
杨 勇
(江苏省镇江市实验高级中学 212003)
1 基本情况
1.1 授课对象
学生来自江苏省四星级普通高中理科班,基础较好,有一定的数学抽象、数学推理和数学运算能力.
1.2 教材分析
所用教材为《普通高中课程标准实验教科书(选修2-2)》(苏教版),“数学归纳法”为第2章“推理与证明”第3节的内容,它是在合情推理的基础上,对归纳出来的与正整数有关的命题进行科学的证明,它将一个无穷的归纳过程转化为有限步骤的演绎过程.它是证明与正整数有关问题的有力工具,是高中数学的一种重要证明方法.通过把猜想和证明结合起来,让学生认识数学的本质,提高学生的抽象思维能力,培养学生科学探索的创新精神.本节课是数学归纳法的第1课时,主要让学生了解数学归纳法的原理,并能够用数学归纳法解决一些简单的与正整数有关的问题.
教学目标 (1)通过对数学归纳法的学习,感受到数学来源于生活而又高于生活,养成善于观察、勤于思考的学习习惯;(2)理解数学归纳法的原理,体会类比、归纳的数学思想,能用数学归纳法证明一些简单的与正整数有关的数学问题;进一步提高数学抽象、归纳猜想能力.
教学重点 数学归纳法产生过程的分析和对数学归纳法证题步骤的掌握.
教学难点 数学归纳法中“以一次逻辑推理替代了无限次验证过程”的理解.
2 教学过程
2.1 创设情境 引入课题
师:我们已经研究了合情推理和演绎推理,现在请同学们用所学知识分析下面的问题.
问题1小明看到树上有几只黑乌鸦,就感叹说:“天下乌鸦一般黑!”小明用了什么推理方法?其结论正确吗?
生1:用了归纳推理,结论不正确.
师:归纳推理有两种,一种是完全归纳,另一种是不完全归纳.准确地讲,小明是用了不完全归纳,要说明结论不正确,我们要举出反例(显示白乌鸦照片).归纳法在现实生活和生产中被广泛应用,比如水文工作者、气象工作者依据积累的历史资料作水文预报、气象预测,用的就是不完全归纳法.
问题217世纪法国著名数学家费马(Fermat)曾认为,当n∈N时,22n+1一定都是质数,这是他验证F0=3,F1=5,F2=17,F3=257,F4=65 537后得到的.
师:后来,18世纪瑞士出了位伟大的数学家欧拉(Euler),证明了225+1=4 294 967 297= 6 700 417×641,从而否定了费马的推测.费马之 所以没有算下去,可能是因为数字太大了,其实下一个数也不是质数:F6=226+1=274 177×
67 280 421 310 721.

(1)求出数列前3项,你能得到什么猜想?
(2)你认为你的猜想正确吗?如何证明?
生3:(自言自语)严格证明不会,但我可以发扬“愚公移山”精神一一验证下去.
生众:(齐笑)虽我之死,有子存焉;子又生孙,孙又生子……
师:发扬“愚公移山”精神,从n=4开始逐个往下验证,精神可嘉,但“子子孙孙,无穷匮也”就为验证这道题,价值不大.我们需要寻求一种方法:通过有限个步骤的推理,证明n取所有正整数都成立.
2.2 实验演示 合作探究
问题4播放多米诺骨牌游戏视频,思考骨牌全倒下,需要哪些条件.
师:看过视频后,请允许我借用一句唐诗来表达一下我的心情:天长地久有时尽,此“牌”绵绵无绝期!游戏者没有一块一块地去推倒骨牌,那是怎么做到让“此牌绵绵无绝期”地倒下去的呢?
生4:必须满足两个条件:(1)第1块骨牌倒下;(2)任意相邻两块骨牌,假如前一块倒下,一定能导致后一块也倒下.
师:条件(2)的作用是什么?
生5:给出了一个递推关系,第一块倒下后依据条件(2),第二块倒下,接着第三块倒下,其他的都能相继倒下.
师:对于条件(2),我们能用数学符号语言表述吗?
生6:k→k+1,k∈N*.
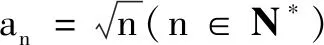
生7:我是这样对比理解的.

多米诺骨牌游戏原理通过有限个步骤的推理,证明n取所有正整数,结论都成立(1)第一块骨牌倒下(1)a1=1成立(2)假如第k块倒下时,一定能导致第k+1块也倒下(2)假如n=k(k∈N∗)时,猜想成立,即ak=k,一定能推出当n=k+1时,猜想也成立,即ak+1=k+1只要保证(1)和(2)成立,那么所有骨牌都能全部倒下根据(1)和(2)可知,对所有的正整数n,猜想都成立
师:通过上述类比,问题得以解决,这就是本节课要学习的数学归纳法.
2.3 引导概括 感悟新知
师:请根据上述的探究过程,概括出数学归纳法的基本步骤.
(板书)数学归纳法 当需要证明一个与正整数n有关的命题P(n)时,可按下列步骤进行:
(1)当n取第一个值n0(=1或2)时结论正确;
(2)假设当n=k(k∈N*,k≥n0)时结论成立,证明当n=k+1时结论也成立.
那么,命题对从n0开始的所有正整数n都成立.这种方法就叫作数学归纳法.

问题5课的开头,同学提到“愚公移山”精神,其中有数学归纳法的原理吗?
生8:有,但愚公家族的无限性是有条件的,即需要“子又生孙,孙又生子;子又有子,子又有孙”.也就是说,倘若愚公及其子孙的每一代都能生出子孙,则愚公家族是无限的.
师:你分析得很好,用数学语言写下来就是:如果愚公本人能够生育男性后代,且第k代能够生育第k+1代的男性后代,则愚公家族是无限的.
师:与此类似,生活中还有放鞭炮、体育课站队等例子.
2.4 数学应用 巩固新知
例1如果数列{an}是等差数列,那么an=a1+(n-1)d对于一切n∈N*都成立,试用数学归纳法给予证明.(证明过程略)
师:能说说步骤(1)和(2)的作用吗?
生9:步骤(1)是递推的基础;步骤(2)是递推的依据.
例2下面用数学归纳法证明1+3+5+…+(2n-1)=n2(n∈N*)正确吗?
证明 (1)当n=1时,左边=1,右边=1,等式是成立的.

生10:错误,第(2)步用求和公式不是数学归纳法,因为证明时没有用到归纳假设.
师:该证法从外在形式上看很具迷惑性,数学归纳法的核心是在验证n取第一个值n0的基础上,由P(k)正确证明P(k+1)也正确,而该同学用的是求和公式,让证明失去了传递性.我们知道,仅有第一步验证而没有第二步传递性的证明是不行的,那么没有第一步行吗?
生11:第一步仅是为了验证当n取起始值n0时结论正确,这是显而易见的,可以省略.
生12:我不同意.第一步是递推的基础,若没有第一步,则第二步就无法进行递推.
师:两种意见截然不同,让我们通过具体例子来说明.
例3试问等式2+4+6+…+2n=n2+n+1成立吗?
生13:成立,因为假设n=k时等式成立,即2+ 4+6+…+2k=k2+k+1,那么当n=k+1时,2+4+6+…+2k+2(k+1)=k2+k+1+2(k+1)=(k+1)2+(k+1)+1,也就是说,当n=k+1时,等式也成立.
生14:不同意,若仅从n=k到n=k+1这一步“递推”来看,似乎无懈可击,但是,当n=1时,左边=2,右边=3,左边≠右边.仔细观察你会发现,该等式左边总是偶数,右边=n(n+1)+1总是奇数,因此对任何的n∈N*该式都是不成立的.
师:两者缺一不可,只有第一步,属不完全归纳法;只有第二步,假设就失去了基础.我们可以把证题过程总结为“递推基础不可少,归纳假设要用到,结论写明莫忘掉.”
2.5 回顾总结 提炼升华
小结:一个数学方法,两个重要步骤,三类思想认识.
师:哪三类思想认识,能具体说说吗?
生15:类比发现,传递相推,有限到无限(辩证思想).
3 教学反思
人们运用数学的眼光观察现实世界,分析研究其中的具体现象,并加以归纳总结,进一步发现内在的结构和规律,这个过程就是“数学化”;数学是思维的体操,数学思考是数学课堂当然的主角.数学课堂应该有数学课独特的味道,学生的数学素养应该在不断品位“数学味”、经历数学化的过程中得以形成和发展.下面结合本节课的教学设计,谈谈本人的一些看法.
3.1 生活问题数学化 飘洒数学味
数学源于生活,也植根于生活,数学化不是脱离生活情境,单纯地就数学而数学,也不是让生活情境仅为引出课题而用,然后弃之不顾,而是要在教学时引导学生从生活问题出发,启发学生类比联想,充分挖掘其中隐含的数学原理,在不断数学化的过程中品味其中蕴含的数学味,逐步抽象出生活问题的数学本质.比如本课中对“天下乌鸦一般黑”“多米诺骨牌”“愚公移山”等生活问题的数学化,归纳出其中的推理方法,就让这些生活问题飘洒出了浓浓的数学味.
3.2 语言表达数学化 体会数学味
数学是自然科学的重要基础,不仅是运算和推理的工具,更是表达和交流的语言.学生通过数学学习和数学应用能学会用数学语言表达世界是新课改提出的目标之一.我们在课堂教学中不仅要培养学生在情境中抽象出数学概念,更要能够进行高度概括和准确表达.如本课中鼓励学生从多米诺骨牌这一生活现象中,先学会用文字语言提炼出“任意相邻两块骨牌,假如前一块倒下,一定能导致后一块也倒下”的内涵,再到符号语言“k→k+1,k∈N*”的高度概括,通过层层设问的方法引导学生不断思考,逐步修正,最后通过类比得出其与数学归纳法原理的一致性,学生在不断体会数学语言的抽象性、准确性和深刻性的同时,数学表达、逻辑推理、数学抽象等素养也得到了提升和发展.
3.3 探究过程数学化 品味数学味
用问题驱动探究,让方法自主建构是提升学生核心素养的有效途径.而问题情境是探究过程得以进行的前提,在设置适合的问题情境后,鼓励学生自主探究,并在独立思考的基础上进行合作交流,让学生通过观察、归纳、抽象、验证、推理等数学手段去探究数学知识的发现和创生过程,在探究和交流的过程中获得对问题的数学化思考,积累数学实践经验.如本课中学生难以理解归纳法中第二步为什么可以根据归纳假设进行证明.鉴于此,师生共同探究多米诺骨牌倒下的原理,并类比此原理,逐步探究出数学归纳法的原理、步骤,培养了学生类比推理、归纳猜想的能力,让学生在这一问题提出、发现、分析和解决的过程中品味其中真切的数学味.
3.4 提炼思想数学化 回味数学味
数学核心素养的形成,不是依赖单纯的课堂教学,而是依赖学生参与其中的数学活动;不是依赖记忆与理解,而是依赖感悟与思维;它应该是日积月累的、自己思考的经验的积累.
本节课上,当多数学生对蕴含其中的“以一次逻辑推理替代了无限次验证过程”这一递推的思想认识还处于肤浅、形式化的直观感觉时,通过构造反例,既使学生在具体的例题中感知数学归纳法的用途,又从本质上理解两个步骤的内在联系,更加体会到:归纳原理中无穷递推的“链条”环环相扣这一数学思想的巨大魅力.数学教学内容是“数学基础知识”“数学方法”和“数学思想”的有机结合,其中数学思想和方法是数学的灵魂,但在教材中大都没有直接的文字表述,往往被教师忽略.这就要求我们在课堂教学中要尽力去挖掘和提炼知识背后所蕴含的数学思想,然后把它巧妙地融入到学习过程中,让学生感悟、体验其中的数学味,在潜移默化中实现学生核心素养的提升.本课中,在笔者的启发下学生总结出:类比发现、传递相推、有限到无限(辩证思想)的数学思想方法,值得大家回味.
史宁中教授在谈到培养学生核心素养时提出:让学生学会用数学的眼光观察世界,学会用数学思维思考世界,学会用数学语言表达世界.其实,综合前文所述,这就是让学生品味数学味,经历数学化.在充满数学思考的课堂上,学习气氛不一定热烈但要深沉,学生不能在喧哗的情境中浮光掠影,要在思索中前行;不是在言说别人的思想,一定是在表达自己的心声.因此,我们数学课堂上要力争去其浮华、探其本质,让学生能感受到躬身前行的姿态,能体悟到生命拔节的声音.

