侧墙窗户对动车组铝合金车体模态的影响*

于庆斌 邵 晴 何玲利

(中车长春轨道客车股份有限公司国家轨道客车工程研究中心, 130062, 长春∥第一作者, 正高级工程师)

随着动车组运行速度的不断提高，以及旅客对动车组乘坐舒适度要求的不断提升，动车组运行的平稳性越来越受到重视[1]。对于动车组车体而言，提升车体低阶模态是提高旅客乘坐舒适度的最佳办法。车体低阶模态的高低既是影响旅客乘坐舒适度的重要因素，同时也是影响车体强度、刚度及疲劳性能的重要指标。

近年来，国内越来越多的专家与学者进行了提升动车组铝合金车体结构模态的研究。文献[2]针对某城际动车组车体模态频率低的问题，通过改进车门位置和尺寸，分析了车体前3阶模态频率随车门位置、车门高度、车门宽度及门框结构形式变化的响应；并根据响应结果重新布置车门的位置和尺寸，使车体模态频率得到了提高。文献[3]分析了动车组车体典型断面的抗弯刚度和外载荷作用下车体的位移响应，总结出动车组铝合金车体结构刚度协调设计原则。文献[4]利用数值微分法计算了某动车组车体主要板件厚度对车体模态频率的灵敏度，使车体1阶垂弯模态频率提高了0.22 Hz。目前，在铝合金车体的设计研究中，还对侧墙窗户结构参数对车体模态的影响进行深入分析和研究。

本文以减轻车体质量并提升铝合金车体结构模态频率至17 Hz以上为设计目标，依据BS EN 12663-1:2010《铁路应用—铁道车辆车体的结构要求》，研究了动车组铝合金车体侧墙窗户结构参数对车体模态的影响。通过对仿真计算结果进行对比分析，提出窗户设置的建议。研究成果可为动车组车体质量减轻的同时提升车体模态频率提供参考。

1 动车组车体结构方案设计

为了研究侧墙窗户结构参数对动车组铝合金车体低阶模态的影响，以某型号动车组的二等座车辆(座椅可旋转)为研究对象，根据总体要求设计了2种窗户结构方案。侧墙窗户的设计需确保在座椅旋转的2个方向上，以及在正常坐姿条件下，旅客可以看到外部景色，以缓解乘坐疲劳。2种设计方案如下：

1) 既有车辆窗户布置方案：每2排座椅对应1个大窗户，每侧布置9个大窗户；大窗户尺寸为1 450 mm×750 mm，窗户间距为2 320 mm。大窗户布置如图1所示。

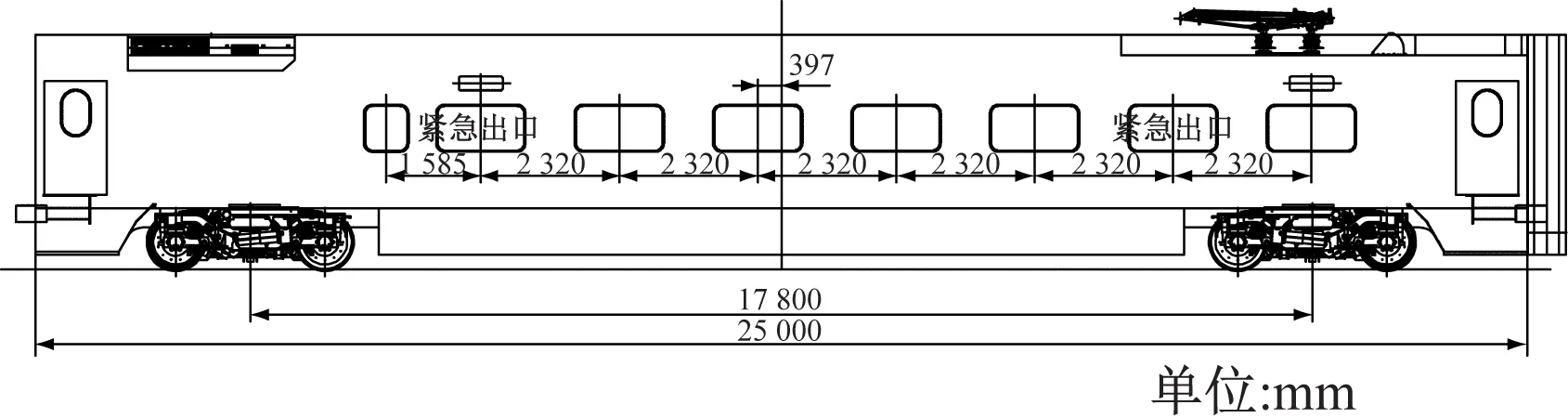
图1 车辆大窗户布置图Fig.1 Layout of vehicle large windows

2) 小窗户布置方案：按照类似于飞机的窗户进行设置，每排座椅对应1个小窗户，每侧布置18个小窗户；小窗户尺寸为500 mm×750 mm，窗户间距为980 mm。小窗户布置如图2所示。

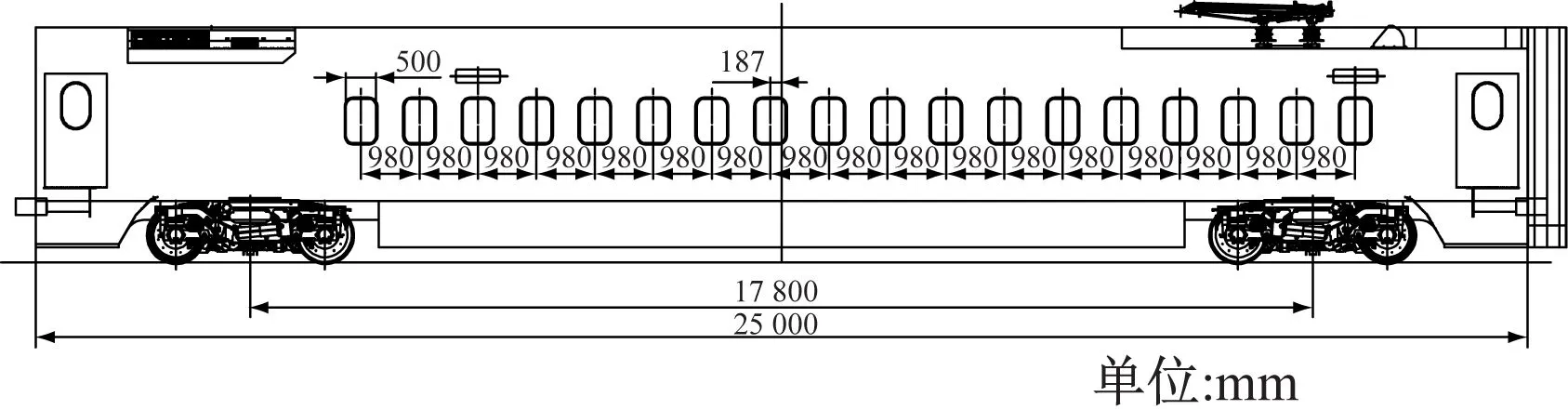
图2 车辆小窗户布置图Fig.2 Layout of vehicle small windows

动车组铝合金车体是由与车体等长的长大中空铝合金型材组焊而成的整体承载结构，其主要材料为铝合金，体积质量为2.7 g/cm3。车体窗户为多层复合结构，面密度为48.5 kg/m2；单个大窗的质量约为44 kg，单个小窗质量约为15 kg；单个大窗需加工的车体铝合金型材质量约为29 kg，单个小窗需加工的车体铝合金型材质量约为10 kg。经计算分析，大窗户较小窗户多去除了约19 kg的铝合金型材，而大窗户较小窗户质量增加了约29 kg。由此可知，小窗方案较大窗方案的车体质量增加约52 kg；但对于车辆而言，单个小窗方案较大窗方案车体质量减少约10 kg，整辆车质量减少约180 kg。

2 动车组车体模态分析

为进一步分析窗户结构参数变化对动车组车体结构低阶模态的影响，分别对2种窗户方案的车体进行了几何建模(见图3)和有限元建模(见图4)。以图4中的大窗户为例，车体结构有限元模型共有2 635 766个节点和5 413 736个单元，包括：1 052个体单元，2 915 754个壳单元，7 956个弹簧单元，2 569 566个质量单元，12个梁单元，以及48个连接单元。

采用Lanczos法分别对2种方案下的车体模态进行分析计算。Lanczos法是将对称矩阵通过正交相似变换变成对称三对角矩阵的方法，也是求解大型稀疏对称矩阵特征值的常用方法。它的原理是先产生1个三对角矩阵Tm，然后将对称矩阵的计算转化为求该三对角矩阵的特征值，这样就使计算变得相对简单。随着m值的增大，Tm的最大特征值与最小特征值会越来越接近原矩阵的最大特征值与最小特征值。

a) 大窗户方案

a) 大窗户方案

动车组车体属于承受多种复杂动力载荷的大型结构，其自振频率和振型主要取决于结构的质量和刚度的分布，通常还要受到支撑情况的影响[5]。基于上述原则和长大中空铝合金型材的长宽比，采用梁单元和壳单元模拟整车结构。为真实表达车体结构的振型, 按实际支撑情况对其施加约束。经有限单元法的离散和变分，并通过求解方程，得到车体结构各阶模态对应的特征值，以及车体模态的振动频率[6-7]。

车体模态振动频率计算输入的基本参数见表1。

经计算，得到2种窗户方案下车体的各阶模态频率(本文重点研究1阶垂弯模态和1阶菱形模态，其他阶模态未列出)。2种窗户方案下车体结构的模态振形及频率见表2。2种窗户方案下车体结构的模态振形见图5～6。经与既有相同车体(大窗户方案)的试验数据(见表3)对比分析得到，计算结果与试验数据误差不超过5%。

表2 2种方案下车体结构的模态振形及频率Tab.2 Modal shape and frequency of car body structures under two window schemes

表3 大窗户方案下车体结构的模态振形及频率试验数据Tab.3 Modal shape and frequency test data of car body structure under large window scheme

图5 大窗户方案车体的模态振形Fig.5 Modal shape of car body structure under large window scheme

图6 小窗户方案车体的模态振形Fig.6 Modal shape of car body structure under small window scheme

由图5～6可知，小窗户方案较大窗户方案的整辆车质量减少约180 kg，小窗户方案较大窗户方案的车体1阶垂弯模态频率提高约6.7%，车体1阶菱形模态频率提高约9.5%。

3 结论

1) 将大窗户改为小窗户后，可以显著提高车体的1阶垂弯模态频率和1阶菱形模态频率，其中1阶垂弯模态频率提高1.12 Hz，1阶菱形模态频率提高1.52 Hz；虽采用小窗户方案时车体质量会增加，但整车的质量会减少更多。

2) 通过对车体窗户尺寸和位置进行设计， 提高了车体模态频率，尤其在整车质量降低的情况下，使车体的1阶垂弯模态频率和1阶菱形模态频率均满足了大于17 Hz的要求。