一道2022年数学竞赛题的多种解法与命题背景探究

虞哲骏 沈珂娜

(浙江省宁波市慈溪中学 315300) (浙江省宁波市镇海中学 315200)

一个好的数学问题常常能激发学生的学习热情和探究欲望，引导数学探究活动有序进行．而一道好的数学题应具备“容易接受、一题多解、蕴含了重要的数学思想、不故意设陷阱、可推广和一般化”这五个特点．2022年全国高中数学联赛四川省预赛第6题就是一道这样的好题．

1 原题呈现

(2022年全国高中数学联赛四川省预赛第6题)若△ABC的三边a,b,c满足a2+b2+3c2=7，则△ABC面积的最大值为．

2 解法探究

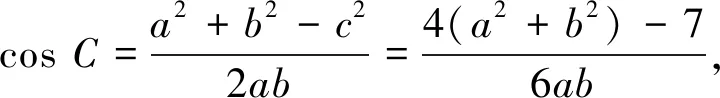
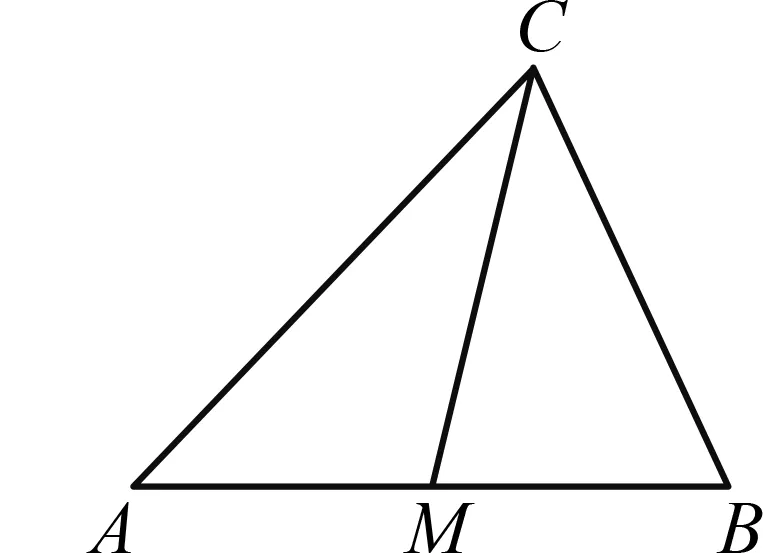
图1

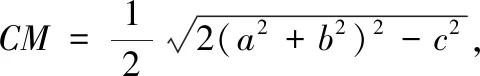
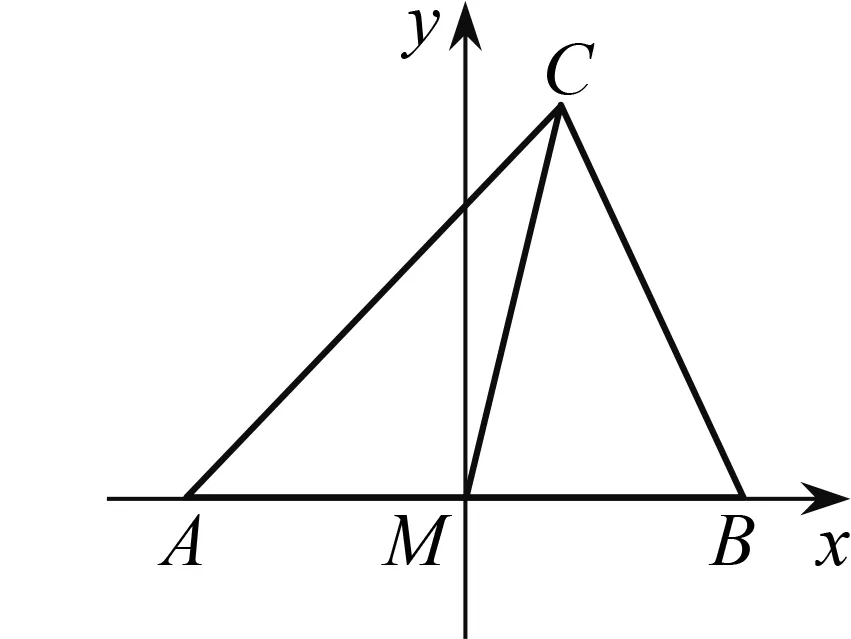
图2

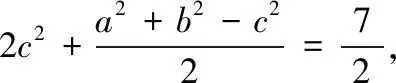
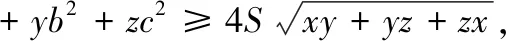
3 命题背景

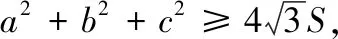
当然，我们也可以利用待定系数法去寻找等号成立的条件：

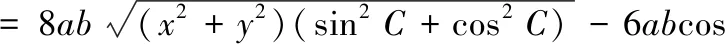
4 结论推广

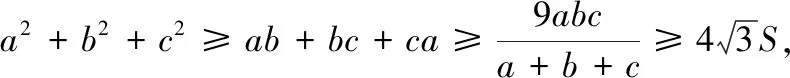
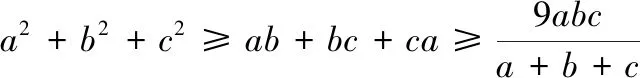
进一步，我们考虑加权的形式，有：

推广2 已知x,y,z>0，若a,b,c为△ABC的三边，S为△ABC的面积，则

当且仅当x=y=z且△ABC为正三角形时等号成立．

证明(1)由外森比克不等式有

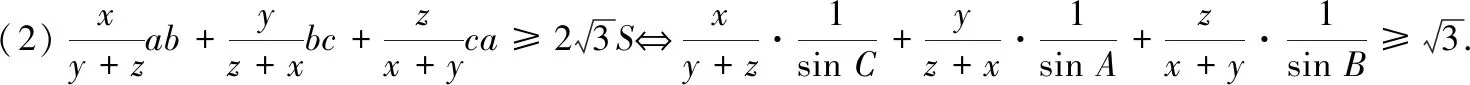
[x(y+z)sinC+y(z+x)sinA+z(x+y)· sinB]≥(x+y+z)2，

每次放假姥爷带我们出门旅游，古玩市场是必去之处。2012年暑假，我们一家去山东日照旅游。返回晋城前我们专门留了一天逛当地的古玩市场，姥爷带着我逛了几家店都没看到想要的制钱。我们又进到一家冷冷清清的店，发现是家瓷器店，转身就要走。老板挽留说有制钱，没想到姥爷还真挑出了他想要的，更没想到老板还赠送了几枚锈迹斑斑的制钱。回家姥爷带我用清水浸泡，拿镊子和毛刷去除土锈后发现竟然有两枚他半年都没寻到的“康熙小全套”中的“臺”，真是“踏破铁鞋无觅处，得来全不费工夫”，捡到大漏了。到此为止，康熙“小全套”就已全部集齐了。

再由柯西不等式得

[x(y+z)sinC+y(z+x)sinA+z(x+y)sinB]2≤[x2(y+z)2+y2(z+x)2+z2(x+y)2](sin2C+sin2A+sin2B)．

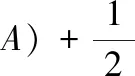
4(x+y+z)4≥27[x2(y+z)2+y2(z+x)2+z2(x+y)2]．而4(x+y+z)4-27[x2(y+z)2+y2(z+x)2+z2(x+y)2]=∑(y-z)2(3x2+2y2+2z2+20yz)≥0，当且仅当x=y=z时等号成立．所以原命题成立．

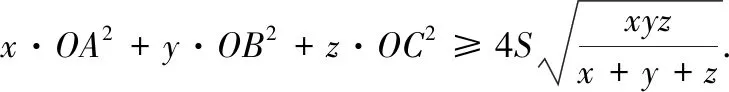
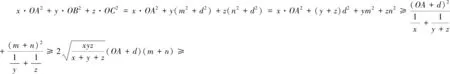
当然，我们也可以从幂次上进行推广：

推广4 若a,b,c为△ABC的三边，S为△ABC的面积，m≥1，则a2m+b2m+c2m≥

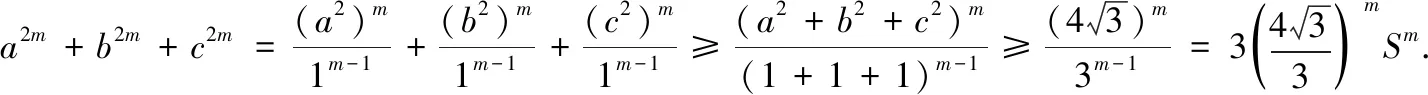
再考虑推广4的加权形式：

证明由柯西不等式，得

(xa2m+yb2m+zc2m)(x+y+z)m-1

=(xa2+yb2+zc2)m

当且仅当x=y=z且△ABC为正三角形时等号成立，从而原不等式成立．

5 结语

在三角形中，我们往往可以借助正弦定理、余弦定理和面积公式结合基本不等式等工具，使解三角形的变化更加灵活．本文对此类边的二次型结构与面积有关的最值问题进行了深入的剖析，并作了一定的推广，显然，根据推广的形式，我们还可以编拟许多习题或考题，来训练或考查学生的数学思维能力．