考虑消费者损失规避行为的“互联网+”回收平台定价决策研究

王竟竟 许民利*

(1.中南大学 商学院,湖南 长沙 410083;2.湖南人文科技学院 数学与金融学院,湖南 娄底 417600)

0 引言

随着经济的飞速发展和科学技术的进步,电器电子产品的更新换代日益加速,电器电子废弃物的数量急剧增加。根据《中国废弃电器电子产品回收处理及综合利用行业白皮书2018》,我国已经成为电器电子产品的生产大国、消费大国和废弃大国。电子废弃物若不合理处置,它们中包含的重金属(例如铜,铝,镉,铬等)会释放到环境中导致空气,灰尘,土壤,沉积物和植物中的重金属严重过量,对自然环境和人类的身体健康产生极大危害[1]。近年来,信息和物联网技术的快速发展给电器电子废弃物的回收带来了新的机遇。2015 年,我国先后颁布《2015 年循环经济推进计划》和《关于积极推进“互联网+”行动的指导意见》,明确提出发展“互联网+回收”新模式,推动电子废弃物市场的转型升级[2]。因此,过去五年中,在政府的大力支持下,“互联网+”回收平台如雨后春笋般涌现,如:爱回收,回收宝,淘绿,乐回收等。

“互联网+”回收是指居民使用互联网平台回收其可回收旧物的回收方式,它将互联网技术整合到资源回收的整个过程中[3],有助于解决传统回收所面临的问题,例如非正式回收者的比例过高[4],回收不便性等。然而,与传统回收不同的是,“互联网+”回收有其独有的特点。首先,信息的不对称,信息不对称表现在一方面回收平台对于参与在线回收消费者持有旧产品的质量等信息不确定,另一方面回收平台对旧产品质检过程的不透明所导致的消费者对在线回收中旧产品可能发生的价值损失等信息的不确定。其次,回收价格的不确定,在“互联网+”回收中,消费者从回收网站获得的旧产品报价并不是最终的成交价格,当消费者根据网站的评价指标对旧产品的预评估与平台的质检结果不一致时,平台会对旧产品进行二次定价,即旧产品的最终回收价格,故消费者在参与在线回收时对旧产品的最终回收价格是不确定的。最后,消费者是否回收行为的不确定,对于预评估和质检结果不一致的旧产品,回收平台进行二次报价后,消费者是否回收除了旧产品质量影响外,部分消费者可能还受初始评估价格等因素的影响而具有不确定性。“互联网+”回收这些独有的特点带来了一些新的问题,例如,消费者担忧平台可能利用质检刻意压低回收价格,低买高卖,以此赚取利润;最终回收价格与平台预估价格之间过高的价格偏差使消费觉得落差过大而不能接受等。这些因素都可能使消费者不选择“互联网+”回收平台或者最终取消在线回收交易。因此,实践中,“互联网+”回收平台对电器电子废弃物的回收率依然低下,远未达到理想的效果。例如,根据知名“互联网+”回收平台“爱回收”大数据提供的数据显示,相对于当年手机的总销量,2017 年“爱回收”对旧手机的回收率仅为1.5%。此外,“爱回收”“回收宝”等“互联网+”回收平台的下载量和用户活跃量远远低于二手综合平台“闲鱼”和“转转”。

要消除消费者的顾虑,在线回收平台需要对不同质量等级的旧产品合理地设置预估价,同时当旧产品的预评估和质检结果不一致时,在线回收平台需要权衡成本损失和产品利润,合理地进行二次定价,最终提高旧产品的回收率和平台的总利润。那么在线回收平台应该如何决定不同质量等级的旧产品预估价及评级不匹配旧产品的二次定价来提高旧产品的回收率和回收平台的利润? 此外,由于预估价的存在,非理性的消费者可能会将平台的预估价默认为旧产品回收价格的参考点,当旧产品的最终回收价格低于预估价时,他(她)会感受到损失。由前景理论可知,消费者在市场中通常对损失比收益会更敏感,即从某个参考点出发,损失规避的消费者对附加费比折扣更加敏感,故当最终回收价格远低于预估价时,消费者本身的非理性行为也会对交易产生很大的影响。例如,在在线回收评价中经常可以看到由于感觉回收平台压价,恶意扣款而最终取消回收交易的消费者。此时,以在线回收平台预估价为参考点,考虑非理性消费者的损失规避行为时,在线回收平台又该如何定价来提高回收率和平台利润?

与本文有关的文献主要有以下两个方面:(1) “互联网+”回收,(2)消费者损失规避行为。对“互联网+”回收的理论研究还处于起步阶段,研究成果较少。已有的研究成果中学者们大多将研究重点放在回收渠道设计,回收渠道竞争和消费者对“互联网+”回收的回收意愿的实证研究上。李春发和冯立攀[5],Feng等[6]研究了具有传统回收和在线回收的双回收渠道二阶段逆向供应链,考虑在线回收渠道消费者偏好的影响。Hahler 和 Fleischman[7]研究了网络回收旧产品的议价过程,并确定产品持有者和网络回收商在博弈中的最佳策略。朱晓东等[8]考虑“互联网+”回收商与传统分销商之间的回收竞争,并分析回收成本差异和可再制造比例对最优定价决策的影响;Taleizadeh 和 Sadeghi[9]研究逆向供应链中具有传统和在线混合双回收渠道供应链与具有单一传统回收渠道供应链之间的竞争。Xiang 和Xu[10]研究闭环供应链中“互联网+”回收平台的动态合作策略。Jian等[11]研究“互联网+”回收模式下的联合回收努力策略。Gu等[12]通过定量的方式来研究“互联网+”回收移动应用程序中回收的城市固体废物的质量和环境性能。

在消费者损失规避行为的研究文献方面,已有研究集中在消费者损失规避行为对新产品销售的影响。Bruce等[13]基于损失规避消费者和品牌选择受品牌相对于多属性参考点位置的影响,对品牌选择进行建模。Nasiry 和Popescu[14]研究具有损失规避消费者和峰终锚定的产品动态定价问题。Heidhues 和Koszegi[15]研究具有损失规避消费者的产品竞争和价格变化问题。Yang 和Xiao[16]基于对服务质量具有损失规避行为消费者,研究供应链的协调机制。基于损失规避的消费者,Wang等[17]研究参考价格对零售商最优定价和库存政策的影响。在线上销售的相关研究中,Ma等[18]考虑具有损失规避的消费者时,制造商是否应该开通线上销售渠道,开通线上销售渠道时如何设置合适的折扣价。Xu 和Duan[19]探讨了消费者的损失规避行为对在线卖家关于定价,订购和快速响应决策的影响。从已有文献来分析,对“互联网+”回收的研究极少有针对“互联网+”回收平台对旧产品定价的研究。此外,当消费者在线上进行购物时,由于产品的不确定性,消费者往往具有损失规避行为,已有文献也进行了相关研究。当消费者在线上进行旧产品回收时,此时尽管产品是确定的,但由于回收价格的不确定性,消费者往往也具有损失规避行为,然而已有“互联网+”回收的研究中极少有文献对此进行相关研究。

综上所述,鉴于已有商业实践和理论研究,本文研究“互联网+”回收平台的最优定价决策问题,且根据回收平台信息充足和不充足的不同情形来建模,并进一步考虑了具有损失规避消费者对最优定价决策的影响,为“互联网+”回收平台进行决策提供有效的管理建议。本文希望能够帮助提高在线回收的参与率和成交率,并增加在线回收平台的收益。

1 问题描述与基本假设

本文研究“互联网+”回收平台对旧产品的最优定价决策问题,在“互联网+”回收模式中,消费者首先通过回收网站对手中持有的旧产品进行评估;其次,根据消费者对旧产品的描述,平台给出预估价,当消费者对预估价满意时他(她)会将手中的旧产品通过邮寄或者上门取件(产生的成本由回收平台承担)的方式交付给平台;第三,由于旧产品描述选项本身的模糊性(例如回收平台中对旧手机描述中屏幕细微划痕和屏幕划伤选项),消费者对产品的评估与平台的质检结果可能不一致,此时平台会对旧产品进行二次定价;最后,若消费者接受二次定价,交易成功,若消费者不接受二次定价,他(她)会退回产品(产生的成本由回收平台承担),平台产生成本损失。基于上述实践的回收交易过程,根据不同的二次定价方式,以下考虑三种情形下“互联网+”回收平台的定价,第一,二次定价时按照旧产品的真实质量等级直接进行定价,称为基本模型,记作B 模型;第二,二次定价时,权衡可能的成本损失和产品利润,对评级不匹配的旧产品重新进行定价,但此时的信息不充分,即评级不匹配的旧产品比例未知,该情形通常出现在“互联网+”回收平台建立初期,称为不完全信息下的二次定价模型,记作SC 模型;第三,二次定价时,权衡可能的成本损失和产品利润,对评级不匹配的旧产品重新进行定价,此时的信息充分,即评级不匹配的旧产品比例可以预测,该情形通常出现在“互联网+”回收平台运行稳定且已有一定的历史交易数据时期,称为完全信息下的二次定价模型,记作C 模型。

为便于模型构建,本文的假设和符号说明如下。

假设1市场中的某种旧产品根据其新旧程度及质量可分为低价值的旧产品和高价值的旧产品,持有低价值旧产品的消费者比例为α,0 ≤α≤1,持有高价值旧产品的消费者比例为1-α。

假设2无论回收交易最终是否成功,回收旧产品产生的运输及检测成本由“互联网+”回收平台承担。回收旧产品的单位成本(快递费,上门取件费,检测费等)记作c。对于评级不匹配的旧产品若消费者选择退回旧产品时,由于时效性及回收平台对电子产品的拆机导致的产品质量下降等,旧产品的价值会有损失,假设退回旧产品价值损失因子为η,0 ≤η≤1。

假设3低价值旧产品的回收价格为pL,可以获得的残值为sL,高价值旧产品的回收价格为pH,可以获得的残值为sH,对于评级不匹配的旧产品二次定价时的价格为p0。

假设4类似Feng等[6]和Wang等[20]的研究,假设消费者对低价值旧产品的回收意愿为θL,对高价值旧产品的回收意愿为θH,θi,i∈{L,H} 均服从[0,1] 上的均匀分布。消费者回收旧产品获得的效用为U。旧产品的回收数量为Qi,i∈{L,H}。

假设5由于回收网站评价指标定义本身的模糊性,评级不匹配表现为:有一部分持有低价值旧产品的消费者在回收平台的价格评估系统中将自己的旧产品评级为高价值的旧产品,假设评级不匹配的旧产品比例为γ,0＜γ≤1。(也有可能持有高价值产品的消费者将自己的旧产品评级为低价值的旧产品,此时回收平台不会再进行二次定价而将它认定为低价值的旧产品,故本文不考虑该情形。)

假设6考虑消费者的损失规避行为时,假设具有损失规避特性的消费者占总的消费者的比例为β(0 ≤β≤1),损失规避的消费者对损失的敏感性系数为δ,对收益的敏感性系数为λ,且δ ＞λ。

假设7()j表示不同模型下的最优定价或者平台利润,j∈{B,SC,C,B*,SC*,C*},其中B,SC,C 分别表示不考虑消费者损失规避行为下的基本模型,不完全信息下的二次定价模型和完全信息下的二次定价模型;B*,SC*,C*分别表示考虑消费者损失规避行为下的基本模型,不完全信息下的二次定价模型和完全信息下的二次定价模型。

2 不考虑消费者损失规避行为时模型的建立

2.1 基本模型(B 模型)

在“互联网+”回收中,回收平台在网页中会通过不同的方式(自己定价或者回收商竞价)对不同质量等级的旧产品进行报价,即根据旧产品的不同质量和使用情况来定价,本文称为初始定价,即预估价。平台收到旧产品后,当预估价与旧产品的质检结果不匹配时,平台进行二次定价。在基本模型中,对评级不匹配的旧产品直接按照其真实的质量等级定价,结合上述交易过程,决策顺序如下:首先,回收平台根据不同质量旧产品的残值和回收成本确定旧产品的初始定价;然后,对评级不匹配的旧产品依据初始定价按照其真实质量等级定价,不再进行重新定价。在初始定价中,持有低价值旧产品的消费者通过回收平台回收的效用为U=pL -θL,持有高价值旧产品的消费者通过回收平台回收的效用为U=pH -θH。则持有低价值旧产品的消费者回收旧产品的数量为QL=pL,持有高价值旧产品的消费者回收旧产品的数量为QH=pH,则“互联网+”回收平台的利润最大化决策模型为:

求解可得如下命题。

命题1在“互联网+”回收中,对于评级不匹配的旧产品,若二次定价时按照旧产品的真实质量等级直接进行定价时,不同质量等级旧产品的最优定价决策如下:

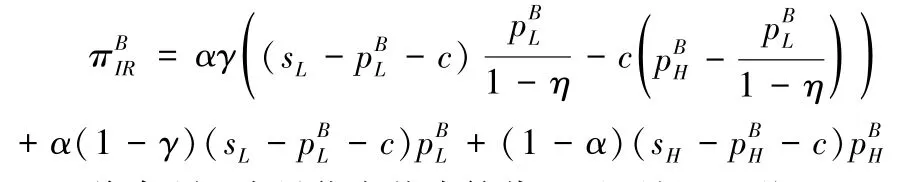
将命题1 中最优定价决策代入后可得“互联网+”回收平台的收益为:

推论1(1)表明,随着退回旧产品价值损失因子增加,退回旧产品的消费者数量会减少,“互联网+”回收平台的利润会增加,但这不意味着回收平台可以通过增加退回旧产品价值损失来提高回收平台的收益,这是因为此处仅考虑一个周期内回收平台的价格决策及利润,短时期内增加的退回旧产品价值损失会使回收平台利润增加。然而,由于参与在线回收到退回旧产品所经历的时间较短,旧产品的时效性造成的价值损失一般不大,造成退回旧产品价值损失的主要原因在于回收平台的拆机等行为,长此以往会使消费者对回收平台的信任崩塌,不愿意再参与在线回收。

推论1(2)表明,当不考虑退回旧产品的价值损失或者退回旧产品价值损失因子较小时,旧产品评级不匹配可能让回收平台产生成本损失,故回收平台的收益随着持有低价值旧产品消费者比例和评级不匹配旧产品比例的增加而减少。推论1(3)表明,当考虑消费者退回旧产品的价值损失,且退回旧产品价值损失因子较大时,回收平台的收益随着持有低价值旧产品消费者比例和评级不匹配旧产品比例的增加而增加。这是因为当退回旧产品损失的价值很大时,一旦消费者参与在线回收,即使是被二次定价,退回旧产品的消费者数量也会减少,从而回收平台的利润会增加。

2.2 不完全信息下的二次定价模型(SC 模型)

实践中,当预估价与质检结果不一致时,回收平台不能简单的按照实际价值进行定价,这样可能造成更多的成本损失,回收平台会对产品利润和损失成本进行权衡来重新定价。在回收平台成立的初期,由于旧产品成交信息的不足,评级不匹配旧产品的比例是未知的。因此,回收平台只能先根据旧产品的残值和回收成本来确定不同质量等级旧产品的初始价格,然后,消费者参与回收后根据已有的成交信息对评级不匹配的旧产品进行二次定价,此时的决策模型称为不完全信息下的二次定价模型,记作SC 模型。决策顺序为:首先,回收平台会先根据产品的残值和回收成本来确定旧产品的初始价格。类似B 模型,最优定价决策为:=(sL -

求解可得如下命题。

命题2在“互联网+”回收中,权衡可能的成本损失和产品利润,当评级不匹配的旧产品重新定价且评级不匹配的旧产品比例未知时,不同质量等级旧产品的最优定价决策如下:

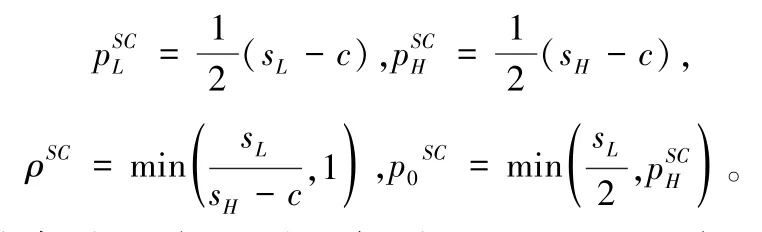
(1)当sH -sL≤c时,

(3)当sH -sL ＞c时,若

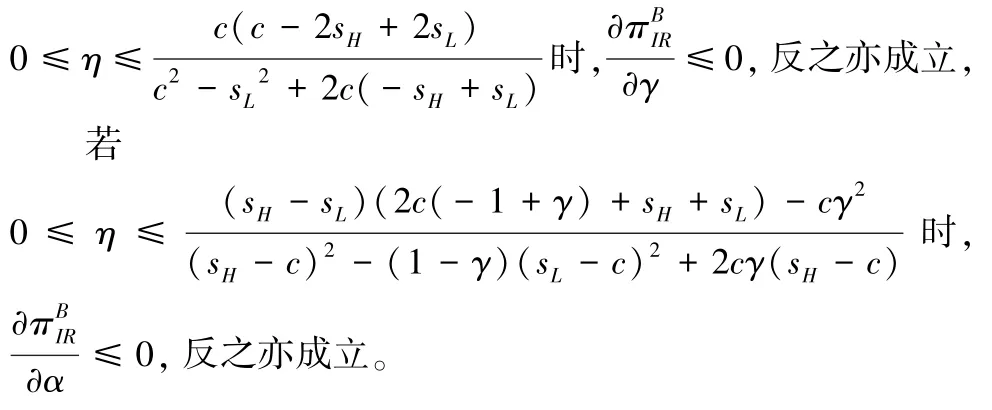
推论2 的结论与推论1 类似,不同之处在于,“互联网+”回收平台关于持有低价值旧产品消费者比例和评级不匹配旧产品比例变动趋势改变的阈值不一致。

2.3 完全信息下的二次定价模型(C 模型)

随着“互联网+”回收平台的发展,历史数据能够预测评级不匹配旧产品的比例。此时,为达到全局最优,回收平台在初始定价时即消费者还未参与回收过程时就会考虑消费者的评级不匹配行为。假设回收平台对评级不匹配的旧产品二次定价为p0,p0≤pH,则只有效用为U=p0-θH≥-ηθH的消费者会达成交易,而效用为U=p0-θH ＜-ηθH且U=pH -θH≥0 的消费者会参与回收但不会达成交易,则“互联网+”回收平台利润最大化决策模型为:

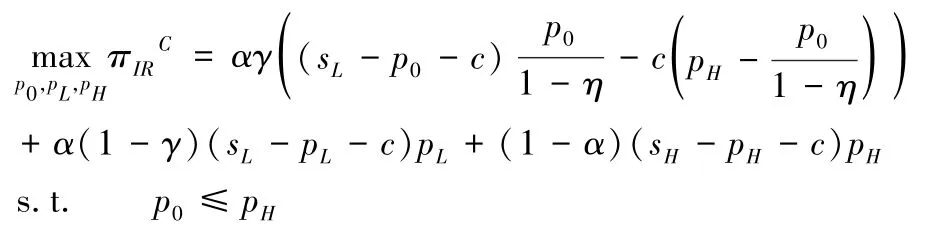
求解可得有如下命题成立。

命题3在“互联网+”回收中,权衡可能的成本损失和产品利润,当评级不匹配的旧产品重新定价且评级不匹配的旧产品比例可以预测时,不同质量等级旧产品的最优定价决策如下:

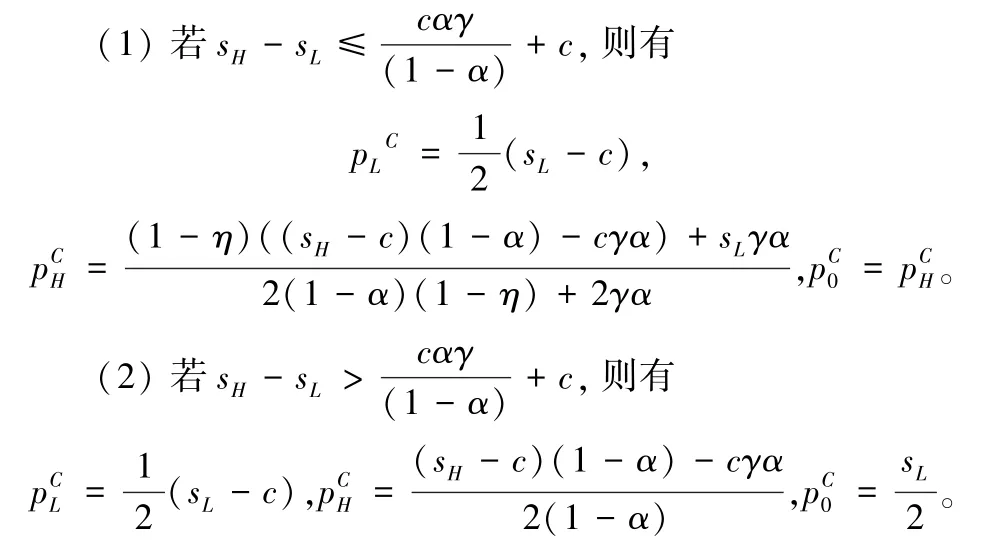
由命题3 可知,类似于命题2,“互联网+”回收平台对旧产品有两种定价策略。当sH -sL≤cαγ/(1-α)+c时,对评级不匹配的旧产品不再重新定价,直接认定为;当sH -sL＞cαγ/(1-α)+c时,重新定价为比真实价格更高的价格sL/2。不同的是,由于“互联网+” 回收平台的发展日益成熟,对于评级不匹配旧产品的比例可以根据历史数据进行预测,回收平台在初始定价时就会考虑评级不匹配的因素来使利润最大化,故此时的高质量旧产品的定价在不同价格策略下不同,且与评级不匹配的旧产品比例、低价值旧产品比例等参数密切相关。此外,相对于SC模型中采取两种策略的阈值,C模型中的阈值更大,即对旧产品不再重新定价,直接认定为的范围增加。将命题3 的最优决策代入“互联网+” 回收平台的利润函数后有:

1.1 社会保险业务发展的基本要求。社会保险工作的开展十分复杂，社保工作的落实会产生大量数据和信息，如果这些信息及数据资料没有进行妥善保管，则会造成数据丢失，对社会保险工作的开展产生阻碍。此外，由于各个企业及单位中经常会出现人才流动的现象，保险缴纳也会产生相应的变动，加强社会保险档案的严格管理，避免社会保险的缴纳出现混乱，人才流动期间会将部分信息资料进行转移，并由新单位予以保管，双方共同协定社保缴纳情况。从体制上来看，保险本身具有严格制度管理体系，社会保险工作与档案管理工作的特征相符合，有利于保障后期工作实施。

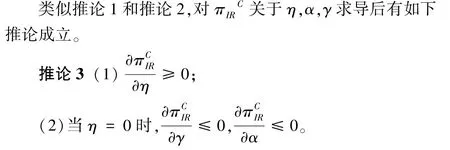
类似于推论1 和推论2,“互联网+”回收平台利润函数关于α,γ的变动趋势与η的取值,旧产品残值及回收成本等参数有关,由于表达式较为复杂,此处不再赘述。

对上述三个模型下回收平台的最优价格和利润进行对比分析,有如下推论成立。

由推论4 可知,在不同模型下低价值旧产品的最优价格是一致的,在完全信息的二次定价模型下高价值旧产品初始定价最低,且评级不匹配旧产品的二次定价最高,而在基本模型中高价值旧产品初始定价最高,且评级不匹配旧产品的二次定价最低。由推论5 可知,“互联网+”回收平台的利润在完全信息的二次定价模型下最高,在基本模型中最低。即回收平台要想获得更高的收益应该要尽可能地减少评级不匹配旧产品的预估价与真实价格之间的偏差,来减少成本的损失和缓解消费者的心理落差,而这可以从两方面实现,一方面是减少高价值旧产品的初始定价,另一方面增加评级不匹配旧产品的二次定价。

3 考虑消费者损失规避行为时模型的建立

心理会计理论[21]提出消费者购买产品的总效用由获得效用和交易效用两部分组成,获得效用取决于该商品对消费者的价值(v) 以及消费者为购买它付出的价格(p),反应了商品的货币价值。交易效用取决于消费者为购买它付出的价格(p) 与参考价格(r) 之间的差别,反应了交易的心理价值。由文献Nasiry 和Popescu[14],Wang等[17]知,此时消费者的效用函数具有如下表达式:

前景理论[22]指出,具有损失规避特性的消费者在市场中对损失比收益会更敏感,即从某个参考点出发,损失规避的消费者对附加费比折扣更加敏感,故在以上模型中有δ ＞λ。对于损失规避的消费者来说,在“互联网+”回收中,预估价在消费者心中已形成参考价格,当回收平台对评级不匹配的旧产品进行二次定价时,消费者获得的总效用中也会考虑二次定价与参考价格的差值。类似于损失规避消费者购买产品获得的效用函数表达式,对于需要进行二次定价且具有损失规避特性的消费者,回收旧产品获得的效用可用以下表达式来描述:

特别地,本节主要分析消费者损失规避行为对“互联网+”回收平台定价及利润的影响,由于退回旧产品价值损失的影响在第2 节中已进行了分析,故这里不再考虑退回旧产品价值损失的影响,即令η=0。

3.1 基本模型(B*模型)

与B 模型类似,在B*模型中,根据残值和回收成本确定的旧产品的初始定价不会发生变化。对于评级不匹配的旧产品,回收平台直接根据旧产品的实际价值进行定价,即p0=pL,故最优价格决策与命题1 相同。不同的是,考虑消费者的损失规避行为时,具有损失规避特性的消费者中只有效用为U=pL -θH -δ(pH -pL) ≥0 的消费者会达成交易,而效用为U=pH -θH≥0且U=pL -θH -δ(pH -pL)＜0的消费者选择参与回收但不会达成最终交易。而对不具损失规避特性的消费者只有效用为U=pL -θH≥0 的消费者会达成交易,而效用为U=pL -θH ＜0且U=pH -θH≥0的消费者选择参与回收但不会达成交易,则“互联网+”回收平台的利润为:

代入命题1 中的最优价格决策后有:

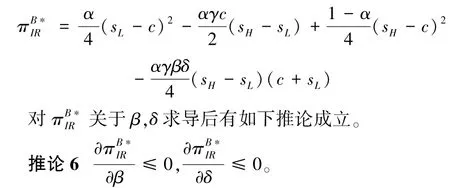
当η=0 时,由于不考虑消费者损失规避行为的B 模型相当于β=0 的B*模型,因此由推论6 可得:

推论7 表明,消费者的损失规避行为对“互联网+”回收平台会产生不利影响,使其利润减少。且由推论6 可知,具有损失规避行为消费者的比例越高或者消费者对损失的敏感系数越大,“互联网+”回收平台的收益会越少。

3.2 不完全信息下的二次定价模型(SC*模型)

求解可得如下命题。

命题4基于消费者的损失规避行为,在“互联网+”回收中,权衡可能的成本损失和产品利润,对评级不匹配的旧产品重新定价且评级不匹配的旧产品比例未知时,不同质量等级旧产品的最优价格决策如下:

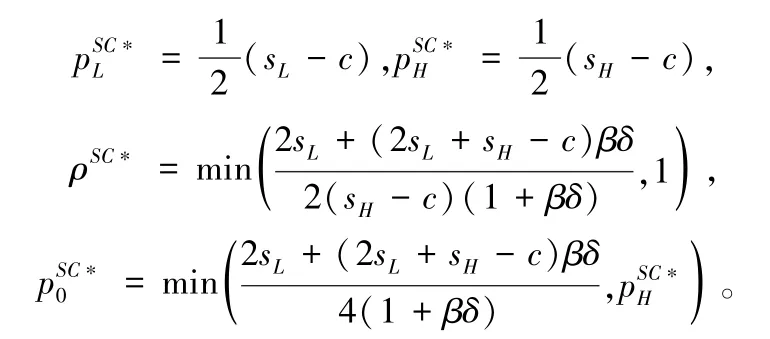
类似于SC 模型,命题4 表明,若“互联网+”回收平台对评级不匹配的旧产品重新定价时有两种定价策略,当(sH -c)/sL ＜2(1+βδ)/(2+βδ)时,对评级不匹配的旧产品价格直接认定为当(sH -c)/sL≥2(1+βδ)/(2+βδ) 时,对评级不匹配的旧产品重新定价,与SC 模型不同的是,由于在可能的成本损失和产品利润的权衡中需要考虑消费者的损失规避特性,此时,旧产品的二次定价与低质量和高质量旧产品的残值,回收成本,损失规避系数有关,且高于SC 模型中的价格sL/2,即由于损失规避特性的存在,为挽回一部分的消费者,回收平台会在二次定价中给出更高的回收价格。将命题4 中的最优价格代入“互联网+”回收平台的利润函数后有:

由推论8 和推论9 可知,不同于B*模型,在SC*模型中,理论上当高价值旧产品的残值远大于低价值旧产品残值时,考虑消费者的损失规避行为下的“互联网+”回收平台可能获得比理性消费者情形下更高的收益,且具有损失规避行为消费者比例越高或者消费者对损失的敏感系数越大,“互联网+”回收平台的收益也越大。这是因为损失规避消费者的存在,回收平台在二次定价中会给出更高的回收价格,从而使更多的消费者会达成回收交易。然而,这种情况要成立需要满足(sH -c)/sL≥2(βδ +1)/βδ,即至少有sH -c≥4sL成立,实践中该条件较难满足。一般来说对于上市时间不长的产品,其不同质量等级的旧产品之间的残值相差会比较大,对于上市时间很长的产品,其旧产品的残值本身比较低,不同质量等级的旧产品之间的残值相差相对较小。而以iPhone11 为例,在“爱回收”的评估中高质量旧产品的预估价为3550 元,低质量旧产品的预估价为900 元(能正常使用,但屏幕刮痕,外壳等破损比较严重),参考此价格取旧产品的残值尚不能满足条件sH -c≥4sL。

3.3 完全信息下的二次定价模型(C*模型)

类似C 模型,在C*模型中 “互联网+”回收平台能够根据历史数据来预测评级不匹配旧产品的比例,故回收平台在初始定价时即消费者还未参与回收过程时就会考虑消费者的评级不匹配行为。此时,回收平台对评级不匹配的旧产品二次定价为p0,p0≤pH,则具有损失规避特性的消费者中只有效用为U=p0-θH -δ(pH -p0)≥0的消费者会达成交易,而效用为U=pH -θH≥0且U=p0-θH -δ(pH -p0)＜0的消费者选择参与回收但不会达成最终交易。而对不具损失规避特性的消费者只有效用为U=p0-θH≥0 的消费者会达成交易,而效用为U=p0-θH ＜0且U=pH -θH≥0的消费者不会达成交易。则“互联网+” 回收平台的利润最大化决策模型为:

求解可得有如下命题成立。

命题5考虑消费者损失规避特性时,在“互联网+”回收中,权衡可能的成本损失和产品利润,对评级不匹配的旧产品重新定价且评级不匹配旧产品的比例可以预测时,不同质量等级旧产品的最优价格决策如下:

(1)当((c+sL)βδ +2c)αγ +(1-α)((1+βδ)(c -sH+2sL)+c -sH)＞0 时,

+2sL)+c -sH) ≤0 时,

类似于SC*模型,命题5 表明,在C*模型中,回收平台对评级不匹配的旧产品重新定价有两种定价策略,将评级不匹配的旧产品价格直接认定为或者对评级不匹配的旧产品重新定价。与SC*模型不同的是,二次定价除了与低质量和高质量旧产品的残值,回收成本,损失规避系数有关外,还与持有低价值旧产品消费者比例及评级不匹配的消费者比例有关。将命题5 的最优价格决策代入后可得“互联网+”回收平台的利润为:

(2) ((c+sL)βδ +2c)αγ +(1-α)((1+βδ)(c -sH +2sL)+c -sH) ≤0

当η=0 时,由于不考虑消费者的损失规避行为的C 模型相当于β=0 的C*模型,进一步由推论10 可得:

类似推论8 和9,由推论10 和11 可知,若“互联网+”回收平台对评级不匹配的旧产品重新定价且评级不匹配的旧产品比例可以预测时,理论上当高价值旧产品的残值远大于低价值旧产品,考虑消费者损失规避行为下回收平台会获得比理性消费者情形下更高的收益,但与SC*模型类似,实践中条件(γcα +(c -sH +2sL)(1-α))βδ+2sL(1-α)≤0 较难满足。对上述三个模型下的最优价格和“互联网+”回收平台的利润进行对比分析有如下推论成立。

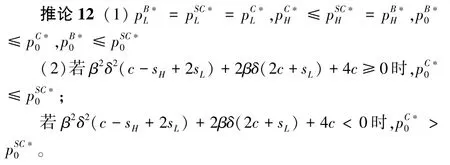
推论12(2)中,条件β2δ2(c -sH +2sL)+2βδ(2c +sL)+4c ＜0 只有当sH远远大于sL才能成立,在实践中较难满足,即通常情况下都有完全信息下的二次定价低于不完全信息情形。这与不考虑消费者损失规避特性的情形中完全信息下的二次定价总是等于不完全信息的二次定价不同,这是因为完全信息下回收平台已经降低了高质量旧产品的初始定价,故不会再过多的增加评级不匹配旧产品的二次定价。

推论13考虑消费者损失规避特性时,在“互联网+”回收平台的两种价格策略下都有

由推论12 可知,在不同模型下低价值旧产品的最优价格是一致的,高价值旧产品初始定价在完全信息的二次定价模型下最低,而在基本模型中最高。评级不匹配旧产品的二次定价在基本模型中最低。不完全信息的二次定价模型中主要通过增加评级不匹配旧产品的二次定价来提高消费者的成交率,而完全信息的二次定价模型中同时通过增加评级不匹配旧产品的二次定价和减少高价值旧产品初始定价来提高消费者的成交率,故由推论13 可知,“互联网+”回收平台的利润在完全信息的二次定价模型下最高,在基本模型中最低。即考虑消费者损失规避时,“互联网+”回收平台要想获得更高的收益还是要尽可能地减少评级不匹配旧产品的预估价与真实价格之间的偏差,来减少成本的损失和缓解消费者的心理落差。

4 数值分析

为使研究结果更为直观,本文进行数值模拟,主要分析“互联网+”回收平台在不同模型下的利润及参数变动对利润的影响。为契合实践,两种不同质量等级旧产品的残值参照在线回收平台的预估价取值,以iPhone6 为例,在“爱回收”回收网站中高质量旧产品的预估价为380 元,低质量旧产品的预估价为150 元(不考虑不能开机,不能使用的情形),故取sH=380,sL=150,按照现有的邮寄费用,假设c=15,此外考虑α变动时,取γ=0.6,β=0.4,δ=0.8,考虑γ变动时,取α=0.4,β=0.4,δ=0.8,考虑β(δ) 变动(由回收平台利润函数知β和δ对利润函数的影响完全一致,故在一个图中考虑)时,取α=0.4,γ=0.6,δ=0.8(β=0.4),由于η变动对利润的影响在推论中已经给出了理论结果,此处不再赘述,并取η=0,数值模拟结果如图1～2 所示。

图1 不同模型下“互联网+”回收平台利润与参数的关系图Figure 1 The relationship between profit and parameters of the “Internet +” recycling platform under different models

由图1 可知,“互联网+”回收平台的利润随着持有低价值旧产品消费者比例的增加而减少,随着评级不匹配旧产品比例的增加而减少,随着消费者损失规避系数的增加而减少。由图2(1)可知,无论“互联网+”回收平台以何种方式来定价,消费者的损失规避特性总是不利于“互联网+”回收平台。由图2(2)和(3)可知,无论消费者是理性的还是损失规避的,“互联网+”回收平台对评级不匹配的旧产品比例进行预测后,在初始定价时即消费者还未参与回收过程时就考虑消费者的评级不匹配行为的情形下可以获得最高的利润。此时回收平台可以通过同时对旧产品的初始定价和二次定价进行决策来减少评级不匹配旧产品和消费者损失规避特性带来的负面影响,且随着持有低价值旧产品消费者比例的增加,通过不同的定价决策模型来增加“互联网+”回收平台收益的效果更明显。

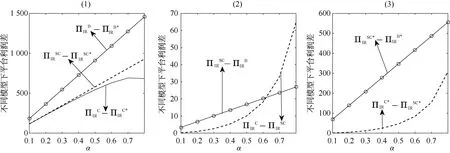
图2 α 变动时“互联网+”回收平台在不同模型下的利润差Figure 2 The profit difference of the “Internet +” recycling platform under different models when a changes

由图1(2)(3)和图2 可知,持有低价值旧产品消费者比例,或者评级不匹配旧产品比例,或者消费者损失规避程度的增加,会扩大完全信息定价决策模型给“互联网+”回收平台带来的正面影响,同时也会扩大损失规避特性给回收平台带来的负面影响,且评级不匹配旧产品比例和消费者损失规避程度带来的这种扩大效应比持有低价值旧产品消费者比例带来的更大。因此,实践中,回收平台可以通过以下方式来提高收益。首先,合理的设置网站的价格评估系统,例如减少不同质量旧产品的等级数来拉开不同等级质量旧产品之间的差距,以避免评价选项的分类过于细致来模糊消费者的选择等,来减少评级不匹配旧产品的比例,从而增加回收平台的收益,并缓解消费者损失规避特性带来的负面影响;其次,在评级不匹配旧产品和具有损失规避行为消费者的存在不可避免的情况下,回收平台应该收集历史数据并对评级不匹配旧产品的比例进行预估,从而通过完全信息下的定价决策模型来增加回收平台的收益,并减少消费者损失规避行为带来的负面影响。

5 总结与展望

本文研究“互联网+”回收平台的定价决策,基于在线回收平台会对评级不匹配旧产品进行二次定价的实践,考虑了三种不同情形下的定价模型:二次定价时直接根据真实的质量等级进行定价模型,评级不匹配旧产品比例不可预测(不完全信息)下的二次定价模型,评级不匹配旧产品比例可预测(完全信息)下的二次定价模型。此外,面对不确定的在线回收价格,消费者往往具有损失规避特性,故进一步考虑了消费者具有损失规避特性时三种不同情形下在线回收平台的定价决策。本文通过对不同模型下回收平台的最优价格和利润进行对比分析,获得的研究结论和管理借鉴如下。

(1)当“互联网+”回收平台对评级不匹配旧产品重新定价时,平台通常可以采取两种定价策略:若不同质量等级的旧产品可获得的残值相差不大时,为避免可能产生的成本损失,对于评级不匹配旧产品可以不进行重新定价;若不同质量等级的旧产品可获得的残值相差较大时,对于评级不匹配旧产品应该进行重新定价,但二次定价应该高于它的真实质量等级对应的价格。

(2)考虑旧产品的时效性及电子产品的拆机造成的旧产品价值损失时,当退回旧产品价值损失因子较小时,回收平台的收益随着持有低价值旧产品消费者比例和评级不匹配旧产品比例的增加而减少。与直觉不同的是,当退回旧产品价值损失因子较大时,回收平台的收益随着持有低价值旧产品消费者比例和评级不匹配旧产品比例的增加而增加。这是因为当退回旧产品的价值损失很大时,一旦消费者参与在线回收,即使是被二次定价,退回旧产品的消费者数量也会减少,从而回收平台的利润会增加。

(3)随着退回旧产品价值损失因子的增加,退回旧产品的消费者数量减少,“互联网+”回收平台的利润会增加,但这不意味着回收平台可以通过增加旧产品的价值损失来提高回收平台的收益。这是因为此处仅考虑一个周期内回收平台的价格决策及利润,短时期内增加的旧产品价值损失会使回收平台利润增加。然而,由于参与在线回收到退回旧产品所经历的时间较短,旧产品的时效性造成的价值损失一般不大,造成退回旧产品价值损失的主要原因在于回收平台的拆机等行为,长此以往会使消费者对回收平台的信任崩塌,不愿意再参与在线回收。

(4)无论消费者是否具有损失规避特性,对评级不匹配旧产品二次定价直接根据真实的质量等级进行定价时,“互联网+”回收平台会获得最低的利润。在评级不匹配旧产品比例可预测(完全信息)的二次定价模型下,“互联网+”回收平台会获得最高的利润。当评级不匹配旧产品比例可以预测时,回收平台应同时确定初始定价和评级不匹配旧产品的二次定价。一方面,应增加评级不匹配旧产品的二次定价;另一方面,应减少高价值旧产品初始定价,最终减少价格偏差,缓解消费者的心理落差,提高消费者的成交率。即在“互联网+”回收平台已积累了一定历史交易数据的今天,回收平台在初始定价中就应该考虑旧产品评级不匹配等因素的影响。

(5)在三种不同情形下,消费者的损失规避行为都会给“互联网+”回收平台带来负面影响,且持有低价值旧产品消费者比例,或者评级不匹配旧产品比例,或者消费者损失规避程度的增加,会扩大完全信息定价决策模型给“互联网+”回收平台带来的正面影响,同时也会扩大损失规避特性给回收平台带来的负面影响,且评级不匹配旧产品比例的这种扩大效应更明显。因此,实践中,回收平台可通过以下方式来提高收益。首先,可以通过合理的设置网站的价格评估系统,例如减少不同质量旧产品的等级数来拉开不同等级质量旧产品之间的差距,避免评价选项的分类过于细致来模糊消费者的选择等,来减少评级不匹配旧产品的比例,从而增加回收平台的收益,并缓解消费者损失规避特性带来的影响。其次,在评级不匹配旧产品和具有损失规避行为消费者的存在不可避免的情况下,回收平台应该收集历史数据并对评级不匹配旧产品的比例进行预估,从而通过完全信息下的定价决策模型来增加回收平台的收益,并减少消费者损失规避行为带来的负面影响。

本文未来还可以从以下两方面进行扩展研究,首先,本文考虑的是短视消费者,未来可以基于策略消费者的行为进一步研究;其次,本文仅考虑在线回收平台的定价决策,未来可进一步考虑在线回收与传统回收竞争时的定价决策。