基于眼动仪的地铁调度员工作负荷评价方法

朱雅茹，杨聚芬，刘志钢

（上海工程技术大学 城市轨道交通学院，上海 201620）

近些年来，由于地铁网络化运营及工作任务复杂化，其作业量、故障场景数量也呈上升趋势，调度员的工作强度随之增强，其责任与压力也在同步加大[1]。调度作业在进行突发事件的应急处理时十分关键，调度员在应急处置场景下处于较为繁重的脑力工作，当脑力劳动处于较高水平时，调度员会因此而产生疲惫、困倦的状态，继而影响其安全作业[2]。因此，为了确保城市轨道交通的安全运行，需要对调度员的工作负荷进行科学的分析与评价。

生理测量方法是基于外设测量的生理指标来进行分析评价操作者的工作负荷，如心率、瞳孔直径、眨眼率等[3]。Weilang[4]及Hasan[5]等运用脑电和光电图技术评估管制员的工作负荷；陈瑜及徐军莉[6]测量了驾驶员在清醒和疲劳状态下的5 种眼动指标，得出PERCLOS、眨眼均值、瞳孔面积作为眼动疲劳特征指标；郭永彩[7]分析疲劳状态下驾驶员的眼动特征参数并提出了基于PERCLOS 的驾驶员疲劳检测方法；靳慧斌等[8]利用眼动指标的共线性，通过回归分析方法建立了基于交互指标的空中管制员工作负荷实时测量方法，但缺少对此模型的验证。本文通过眼动仪采集调度员在工作状态下的9 个眼动指标，使用单因素方差分析法筛选出5 个与工作负荷显著性相关的指标，将显著性指标进行因子分析并提取出综合因子，以工作负荷作为因变量，综合因子作为自变量对工作负荷回归模型进行参数标定，建立地铁调度员工作负荷评价模型，最后采用实测数据对该模型的有效性进行验证。

1 基于眼动的工作负荷评价原理

城市轨道交通调度系统是一个人机交互的系统，调度员需长时间盯视监控面板以防忽略列车故障情况，单一的工作内容会使得其产生枯燥的心理情绪从而影响其视觉注意力。当列车发生故障需应急救援处置时，调度员需针对状况思考短时间内做出决策，当列车突发情况较为频繁时，调度员会长时间处于注意力高度集中，在此过程中人的脑力劳动会逐渐增多，因此长时间监控作业会使得调度员的工作负荷会逐渐发生累积[9-11]。本文采用实验的方式，实时采集调度人员在监控任务及应急处置情景的眼部动态变化指标，对指标变化进行分析。

人所接收到外界信息有80%均通过眼睛所建立的视觉通道来获取的，人在进行生理或心理活动时，眼睛可以反映其活动过程[12-13]。研究表明，当人进入疲劳状态时，其眨眼潜伏期、闭眼时间占比、凝视时间、瞳孔扩张情形、CA 均会发生增加[14]，因此调度员的眼动指标可以反映其在与工作环境交互时所获得的信息量及自身心理活动。因此本文通过实验采集的眼动数据建立模型来评价调度员的工作负荷，对采集到的平均眨眼率、平均凝视时间、平均凝视次数、平均扫视时间、双眼平均扫视角度、双眼平均扫视次数等9 个指标进行分析，使用方差分析法筛选出平均眨眼率、平均凝视时间等5个显著性指标并进行综合因子的提取，以主观负荷作为因变量、综合因子作为自变量进行工作负荷回归模型的参数标定，建立地铁调度员工作负荷回归模型。

2 实验设计

2.1 实验目的

为获得调度员工作过程中不同状态下眼部变化的特征参数，应用Dikablis Glass 3 眼动仪设备采集调度员在模拟环境下的眼动指标。

2.2 实验设计

本次实验设计三种不同难度的作业任务，如图1 所示。被试需要依次完成三组实验，最终保证故障列车的救援处置过程完成，在实验过程中，每组实验完成后，被试需填写NASA-TLX 量表并休息10min。

图1 作业内容等级图

2.3 实验设备

本实验使用Dikablis Glass 3 眼镜式眼动仪，采样率为60Hz（Per eye）。实验环境为基于动态场景的轨道交通行车调度虚拟仿真实验系统，如图2 所示。

图2 基于动态场景的轨道交通行车调度虚拟仿真实验系统

2.4 实验过程

为了避免被试实验结果受时间段选取的不同而受影响，每位被试的实验均在上午9:00～11:00 期间进行。实验开始后，被试依次进行三种不同难度的作业任务，每次实验期间休息10min，并填写NASA-TLX 量表，对该次任务工作负荷的大小做出主观评定。如图3 所示。

图3 被试实验状态

3 基于眼动特征的调度员工作负荷评价方法

3.1 眼动指标的分析

（1） 关键眼动指标的筛选

本次实验共采集到9 个眼动指标：单个被试的实验持续时间、眼部数据在画面中的X 轴坐标的标准差、眼部数据在画面中的Y 轴坐标的标准差、平均眨眼率、双眼平均凝视时间、双眼平均凝视次数、双眼平均扫视时间、双眼平均扫视角度、双眼平均扫视次数。为了剔除对工作负荷（实验中使用任务难度表征） 无显著性差异的指标，以任务难度为自变量，以9 种指标为因变量，分别进行单因素方差分析，结果如表1 所示。

由表1 可知，眼部数据在画面中X 轴坐标的标准差、眼部数据在画面中Y 轴坐标的标准差、双眼平均扫视时间、平均扫视角度的方差分析P 值均大于0.05，即4 种指标在不同的任务难度下数据变化无显著性差异。

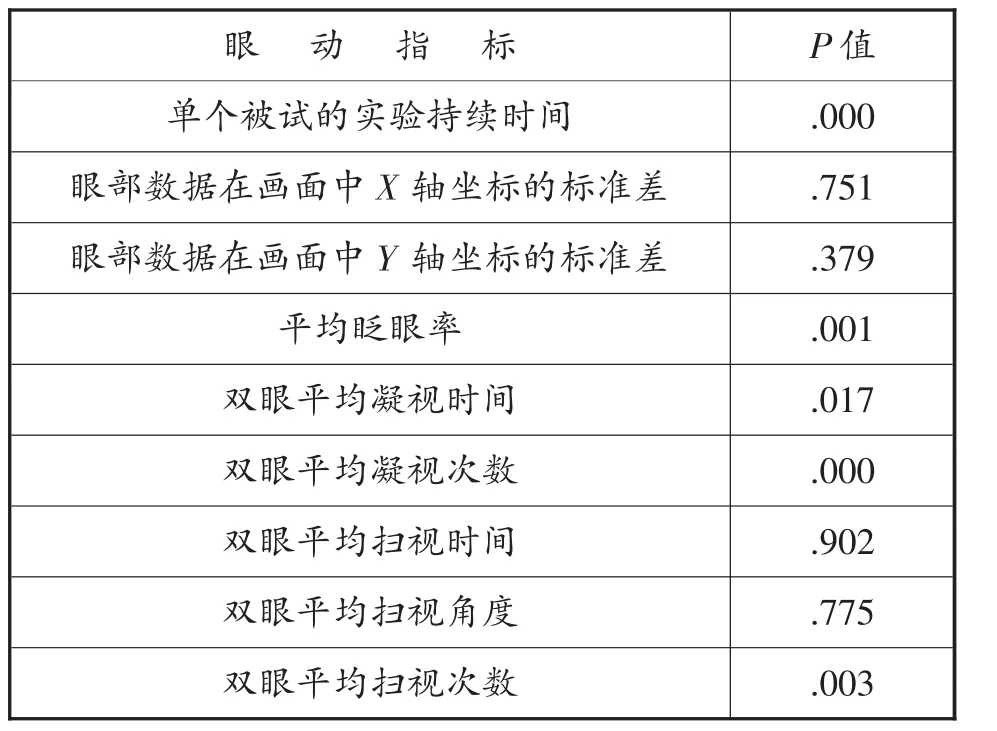
表1 单因素方差分析结果

（2） 眼动指标综合因子提取

为了检验各关键指标之间相关程度，对其进行KMO 和Bartlett 检验，结果分别为0.628、0.001，表明关键指标间存在相关性，不能直接用于拟合工作负荷回归模型。针对此，本文首先应用因子分析法提取出能表征关键指标的综合因子，再构建综合因子与工作负荷的回归模型。因子分析结果只提取出1 个综合因子W1，累积贡献率为74.92%，且W1与5 个关键指标间的解析关系为：

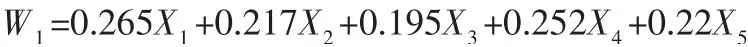
其中：X1、X2、X3、X4、X5分别表示实验持续时间、平均眨眼率、双眼平均凝视时间、双眼平均凝视次数、双眼平均扫视次数。

3.2 基于眼动指标的调度员工作负荷评价

回归分析是指利用数据统计原理，对大量的统计数据进行数据处理，进而确定因变量和自变量的相关关系，建立一个回归方程便于预测由于相关指标的变化所引起的模型变化的结果。本节以NASA-TLX 量表所计算的主观负荷值以及利用因子分析方法所得出综合因子W1分别作为因变量和自变量，进行回归分析。

R2是度量拟合优度的统计量，本节回归分析中R2的值为0.663，代表着综合因子W1对于因变量NASA 值的拟合效果为66%，且综合因子W1与因变量NASA 值的方差分析检验结果为0.00，说明综合因子W1与因变量NASA 值存在显著性线性关系。

根据回归分析的系数可知，综合因子W1对于因变量NASA 值存在正方向影响，结合表2 中系数可得调度员工作负荷的预测模型表达式，即：

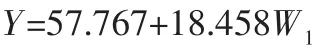
表2 回归系数表

德宾-沃森检验简称D-W 检验，是目前检验自相关性最常用的方法，但它只使用于检验一阶自相关性，在此回归模型的残差分析中，德宾-沃森的指数为0.784，可以认为残差间存在弱自相关性；VIF（容差的倒数） 用于共线性诊断（变量之间的关联度），该项统计值为1，代表不存在多重共线性。通过观测由SPSS 绘制的标准化残差P-P 图，如图4 所示，可以观测散点大部分聚集在对角线附近，因此可以认为残差符合正态分布，除此之外根据回归标准化残差图的分布规律分析，若残差的分布随回归值的改变而发生规律性的变化则代表方差性的假设存在问题或存在异常值，通过图5 所示回归残差图，不论回归值的大小，而残差具有相同的分布，因此满足模型的各假设条件。

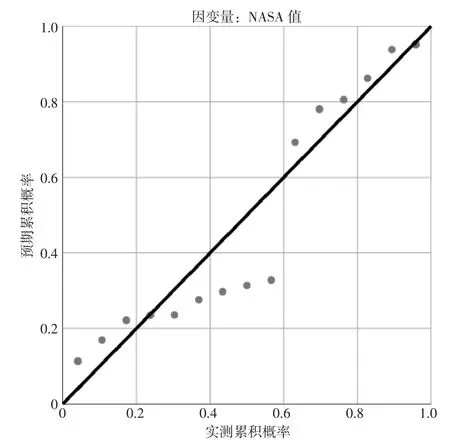
图4 回归标准化残差的正态P-P 图

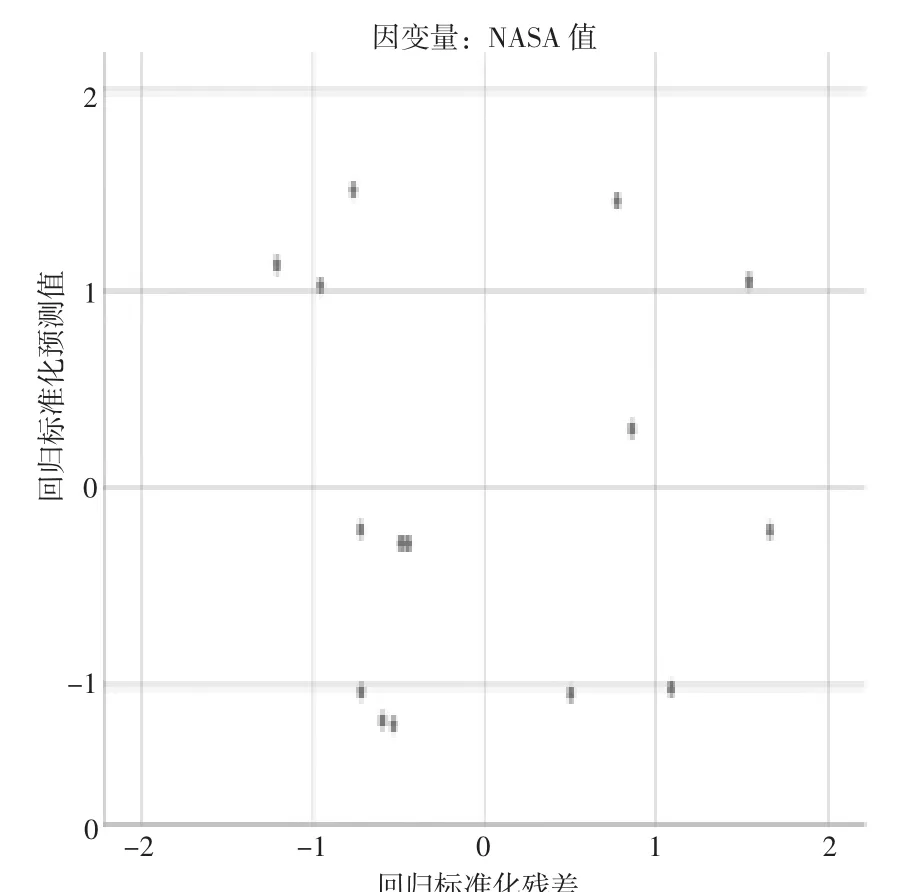
图5 回归标准化残差图

3.3 模型验证

实验共获取7 位被试的数据，其中5 人被分为实验组，2 人分为测试组。在上文中，通过实验组5 位被试的数据建立了调度员工作负荷的回归模型，本节将利用测试组2 位被试的数据进行回归模型的验证。验证前，2 位被试的眼动数据进行了标准化处理，将处理后的数据代入回归模型，将测得的数据与其主观负荷绘制为折线图，如图6 所示，两者数值较为接近，验证了本文负荷评价结果的有效性和准确性。

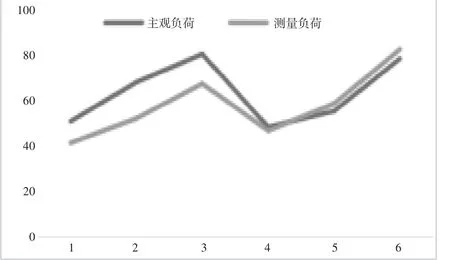
图6 预测结果图

4 总 结

本文对地铁应急处置场景下地铁调度员的眼动数据进行采集及分析，建立了调度员的工作负荷评价模型，该模型所得数据可有效反映调度员的工作负荷水平，为地铁调度员工作负荷状态评价提供研究基础。