闭环供应链锦标激励机制研究

陈亚兰，朱卫平，胡仁杰

（上海工程技术大学 航空运输学院，上海 201620）

闭环供应链是指企业从采购到最终销售以及废旧产品回收的完整供应链循环，包括产品回收和生命周期支持的逆向物流[1]。近年来，我国在科技和创新等方面取得了巨大进步，经济建设的高速发展一方面提高了人们的物质生活水平，另一方面也促进了技术的不断变革，加速了产品的更新换代，环境污染和资源枯竭问题日趋严重。在诸多政策和国际形势的推动下，回收再制造已成为企业未来发展的重要考量因素，发展闭环供应链已是大势所趋。

许多学者对供应链委托代理问题展开了研究。Savaskan[2]建立了以制造商为委托人，零售商为代理人的委托代理模型。孙宝风等[3]和关启亮等[4]建立了闭环供应链多任务委托代理模型。而一些学者认为在供应链合作中，大多数合作模式是不稳定的，易发生机会主义行为，但通过引入相互竞争机制，可有效降低机会主义行为[5]。如一些上游企业通过对其下游企业进行诸如星级评选并设置一定比例的奖金以引导下游企业相互竞争，从而有效激励和管理下游企业，这实质就是锦标制度。

自Lazear 和Rosen[6]首先提出锦标制度以来，其研究及运用已不仅局限于“成功者”和“失败者”之间的报酬差距，在员工晋升管理、供应链激励等领域也有着广泛的应用[7]。Lazear 等[6]认为锦标制度可以消除更多的不确定因素，减少道德风险所带来的问题，降低风险成本，增强委托人对代理人的激励强度。李雷[8]建立了供应链锦标激励模型。相关的研究[7-9]给予了本文启发，文中运用锦标制度和多任务委托代理模型，构建闭环供应链锦标激励模型，对激励机制的重要性质进行研究。

1 激励模型建立

为便于分析，主要考虑由1 个制造商和2 个零售商构成的二级闭环供应链，零售商负责新产品销售和废旧产品回收两项任务，其中销售活动易于观测和控制；回收活动不易观测和控制[3]。为最大化自己的利润，制造商通过设计有效的激励契约激励零售商在两项任务上的投入，提高供应链系统的激励效能。

2 激励模型求解

首先求解的第一步是当零售商面对委托人制定的激励契约，其选择的最优努力水平。

2.1 零售商的最优努力水平分析

2.2 最优激励方案分析

模型求解的第二步则是制造商在满足零售商的最优选择的约束下，设定最优的激励方案Δ。制造商的目标函数如下：

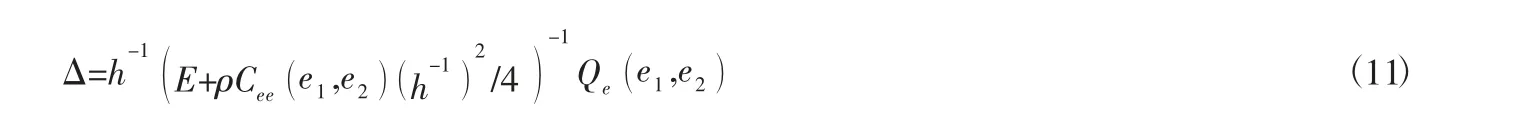
3 模型性质分析

3.1 任务相互独立下的模型分析

根据文献[3]的假设，如果零售商的两项工作任务相互独立，即Cij=0（i≠j 时成立） 代入式（11） 可化简为：

在这种情况下，多任务锦标激励模型变为两个单任务锦标激励，且激励强度等于零售商只执行某一项任务时的激励强度。

（1） 求解可知∂Δj/∂ρ＜0，Δj与ρ 是负相关的。这说明对于风险规避的零售商，制造商在制定激励方案时应考虑适当增大绩效激励。一般来说，初入市场的小型零售商具有较高的激情，渴望在市场中占有一席之地，具有更高的风险偏好，所以制造商对于初入市场的零售商应当将激励差额变小，而对已在市场中稳定发展的企业则应当将激励差额加大。

（2） 求解可知∂Δj/∂Cjj＜0，Δj与Cjj是负相关的。这说明假如某项任务的单位激励成本低，则应当提高对其业绩的激励，反之，则应该降低对其业绩的激励。如随着社会进步，低碳环保的观念也逐渐深入人心，这时零售商只要稍加努力就可以提高业绩，努力成本相对较低，这时制造商可加大激励强度，即扩大激励差距，激励零售商增加努力水平。

3.2 任务相互依存下的模型分析

在实际中，零售商既要考虑销售收益还要考虑回收收益，而文献[3]认为多数情况下零售商承担的两种任务间努力成本具有替代关系。故文中假设两项任务在零售商的成本函数中具有替代性，将C12=C21＞0 代入式（11） 计算可得：

（1） 求解可知∂Δ1/∂ρ＜0，Δ1与ρ 负相关的，这说明对于风险规避的零售商而言，就收益的动荡性与收益的稳定性来说，他会更偏向于稳定性。所以对于ρ 较高的零售商，Δ1大小对于其激励作用不大，所以制造商应适当降低最优激励差额，确保自己的收益最大化。

（2） 求解可知∂Δ1/ΔQ2＜0，Δ1与Q2是负相关的，这说明如果制造商认为零售商追求回收任务会带来更多的收益，那么他就会减小销售任务的激励差额，从而避免零售商将过多的精力投向销售任务，而忽视回收任务。因为随着资源短缺问题日益严重，如何实现可持续发展是国家重点研究问题，政策和法规约束和规范制造商进行回收再制造。

（3） 求解可知∂Δ1/∂h1[0 ]＜0，Δ1与h1[0 ]是负相关的，这说明销售任务的可观测程度越大，制造商可获得的信息越多，制造商就应该减小销售任务的激励强度，最优激励差额变小，对零售商的激励作用变弱，零售商会更倾向于依靠自己的主观性来选择努力水平，如果某一零售商想获胜，那么零售商就会提高努力水平，此时，制造商节约了激励成本。

4 数值分析

4.1 任务相互独立时激励性质分析

为简化计算，对于式（12），参考文献[4]的取值，设ρ∈[1,1 0 ], Cjj∈[1,1 0 ], Qj∈[1,2 5 ], hj[0 ]∈[1,2 0 ]，假定初始值ρ=3, Cjj=5, Qj=10, hj[0 ]=1。在此基础上，运用Matlab 软件分析其变化趋势，如图1 所示。从图1 中可知Δj与Cjj和ρ 是负相关的。对比图1 中a 和b 两条曲线，并结合图2，这说明ρ 和Cjj对Δj的影响差距不大。这跟上述结论是一致的。

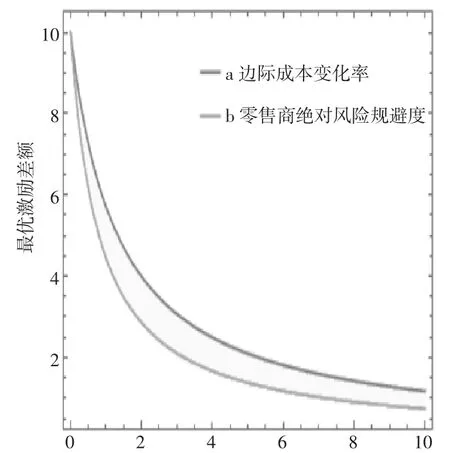
图1 任务独立下Δj随Cjj和ρ的变化趋势图

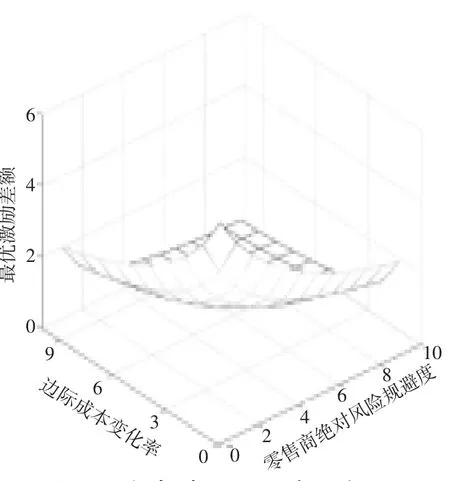
图2 任务独立下Δj随Cjj和ρ的变化曲线

4.2 任务相互依存时激励性质分析

同理，对于式（14） 的分析，设ρ∈[1,1 5 ], Cjj∈[1,1 0 ], Qj∈[1,2 0 ], h1[0 ]∈[1,2 0 ], 初始值ρ=2, C11=C22=10, C12=C21=7, Q1=8, Q2=3, h1[0 ]=4。运用Matlab 软件分析任务相互依存下Δ1随ρ、Q2、h1[0 ]的变化趋势，如图3 至图6 所示。结合图3 至图6 中可知Δ1与ρ、Q2、h1[0 ]是负相关的，这跟上述模型分析中的结论一致。但三者负相关的效果存在差异，图3 中e接近直线，可以理解为Δ1随着ρ 等比例递减，而图3 中c 跟d 是曲线，但陡峭程度不同，但也是负相关的。

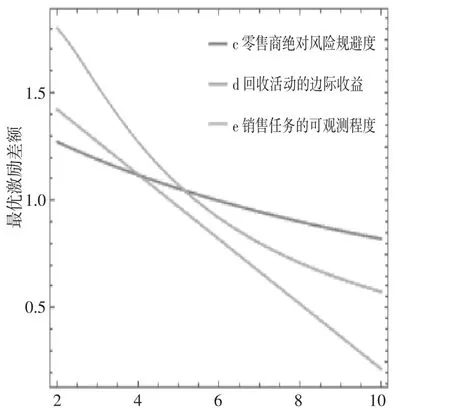
图3 任务依的存变下化Δ趋j随势ρ图、Q2、h1 [0]

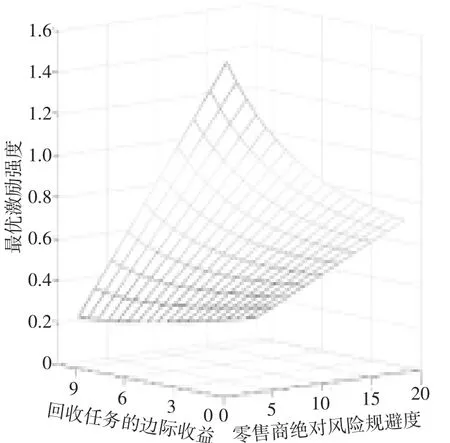
图4 任务依存下Δj随ρ、Q2的变化曲线

图5 任务依存下Δ1随Q2、h1 []0的变化曲线

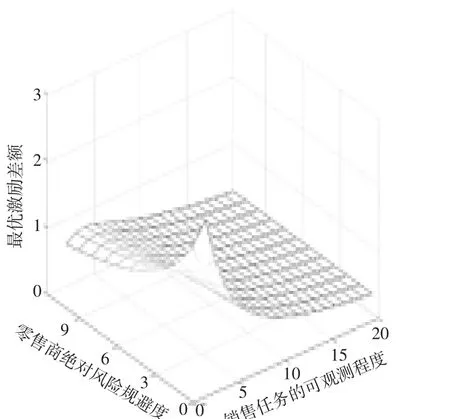
图6 任务依存下Δ1随ρ、h1 []0的变化曲线

5 结 论

基于锦标制度和多任务委托代理模型，设计了闭环供应链锦标激励机制，通过对模型的分析，得出以下结论：（1） 在锦标激励中，零售商关心的是高报酬和低报酬之间的差值。（2） 当两项任务的成本函数是相互独立的，那么多任务锦标激励机制就转变为单任务锦标激励机制。（3） 当两项任务的成本函数是相互替代的，制造商对于销售任务的最优激励差额要小于零售商只承担销售任务时的激励差额，且回收任务的最优激励差额跟回收效益、风险规避度、销售任务可观测度是负相关的。

基于上述结论，得到如下管理启示：信息不对称条件下，最优激励契约要求制造商承担更多的风险，在激励零售商时应充分考虑各方面的因素，激励差额应根据不同情况制定不同方案，这对建立长期稳定的合作关系具有积极指导作用。