基于DIC 技术的固体火箭发动机装药粘接界面参数反演研究

肖云东，王玉峰，李高春，孔令泽，伍 鹏，赖帅光

（1. 海军航空大学，山东 烟台 264001；2. 91468 部队，海南 陵水 572400；3. 91526 部队，广东 湛江 524000）

0 引言

固体火箭发动机作为各类飞行器的动力装置，具有贮存时间长、使用方便、结构简单等优点，在航空航天等领域被广泛使用［1］。但固体火箭发动机的推进剂/衬层/绝热层界面易脱粘［2］，所产生的故障约占发动机总故障的1/3［3］，这是影响固体火箭发动机能否正常工作的关键问题，也是对其开展有限元仿真的难点。

大多学者采用内聚力模型对粘接界面的脱粘行为［4-6］进行有限元仿真，准确的内聚力模型是获得有效仿真结果的重要前提。当前，关于如何确定内聚力模型的相关研究较少，大多预先定义模型种类，模型参数再通过经验法、实验法、反演识别（有限元模型修正技术）等方法确定。常见的实验法有：J 积分法［7］、“含能力”的平衡法［8］、直接拉伸法［9］。前2 种方法仅适用于线弹性材料；后一种方法则需试样在各处损伤一致，这在实验中几乎不可能实现。

学者们基于仿真与实测数据信息，采用反演识别方法获取内聚力模型相关参数的做法较为常见。例如：伍鹏等［4］基于仿真与实验获取的应力-应变数据信息构建目标函数，再通过分步反演与Hooke-Jeeves 优化算法［10］相结合的方法，求解了内聚力模型相关参数。饶玉文等［11］基于仿真与实测的载荷-位移曲线信息构建目标函数，通过人工蜂群优化算法，确定了双线性内聚力模型［12］相关参数。Chen X 等［13］采用改进的Levenberg-Marquardt 算法［14］，确定了2024-T3 铝合金断裂损伤界面内聚力模型的参数，使荷载-裂纹扩展关键点的模拟预测值与实测值的差异最小化。学者大多通过载荷-位移相关数据开展反演研究，仅能反映出试件的宏观力学行为，无法反映局部信息，而且该方法的约束性较高，需基于应变场均匀性假设。通过感兴趣区域（Region of Interest，ROI）位移场的相关数据信息开展反演研究可对上述问题进行有效改善。同时，基于数字图像相关技术（Digital Image Correlation，DIC）技术获取的位移场/应变场中包含了大量的材料响应数据，在统计意义上使反演获得的参数准确性高于常见的载荷-位移构造方法。DIC 技术具有全场非接触性、适用范围广等优点，已成为一种有效的表面变形非接触测量方法，可实现变形区域位移的量化分析［15］，已广泛应用于力学实验领域。李高春等［16］采用DIC 技术对扫描电子显微镜获取的复合固体推进剂拉伸变形图片序列开展计算，获得了推进剂细观表面位移场。Gonzalez J 等［17］采用DIC 技术分析了复合固体推进剂裂纹尖端附近的应变场特点。

针对以载荷-位移曲线信息开展反演研究时，存在的局限性以及数据类型单一、数据量小的问题。本研究采用基于DIC 技术结合Hooke-Jeeves 优化算法，以固体火箭发动机矩形粘接试件单向拉伸实验中的实测数据（ROI 位移场和应力-应变曲线）为依据，建立表征粘接界面真实本构关系的双线性内聚力模型，为粘接界面的力学行为分析提供理论基础和参考依据。

1 基本理论

1.1 数字图像相关技术

DIC 技术依据图像中各像素点周围区域的散斑分布情况不同的特点，按照定义的相关函数和搜索方法在目标图像中确定与参考子集相关性最大的目标子集，从而实现物体表面位移的测量［18-19］。一阶位移模式下，参考图像像素点与目标图像像素点关系示意图，如图1 所示。

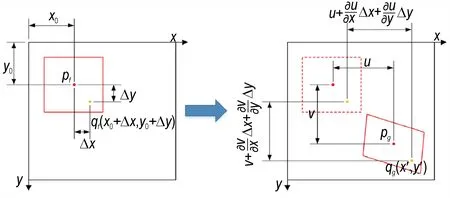
图1 一阶位移模式示意图Fig.1 Schematic diagram of first-order displacement pattern

参考图像像素点与目标图像像素点坐标对应关系，如式（1）：

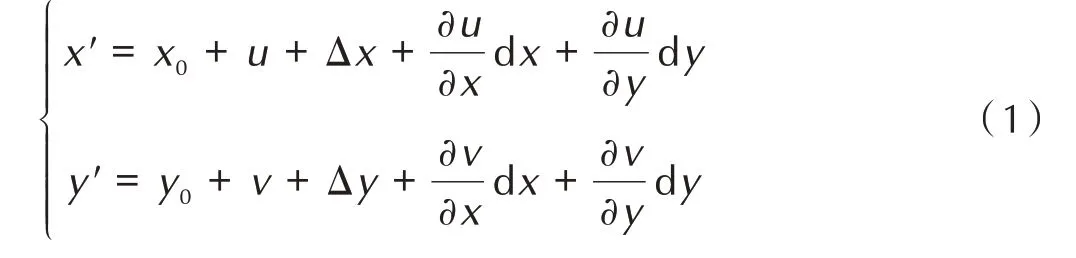
目标图像中需确定与参考图像ROI 相关性最大的目标区域，通过变形前后子集的相关性计算，作为匹配程度的标准，采用归一化最小二乘相关函数［20］表征匹配程度，如式（2）：

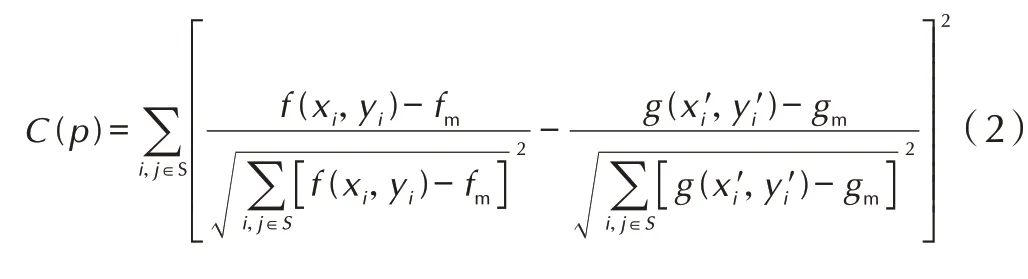
式中，C为归一化最小二乘相关函数，数值越趋近于0，子集匹配程度越高；S 表示子集区域；f（xi，yi）为参考图像中像素点（xi，yi）的灰度值；g（x′i，y′i）为目标图像中像素点（x′i，y′i）的灰度值；fm与gm分别为参考子集与目标子集的平均灰度值。子集的变形矢量P，如式（3）：

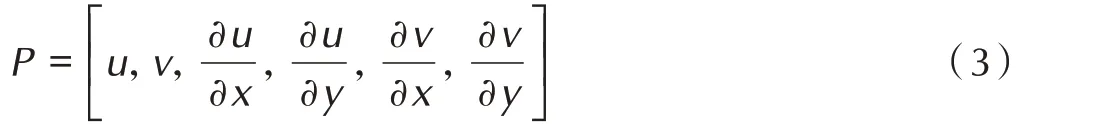
在运算求解过程中，目标子集与参考子集不会完全匹配，通过搜索算法寻找相关函数的极值，从而确定匹配程度最高的目标子集，对相关函数C（p）求关于ΔP的偏导数，并令其等于0，如式（4）：

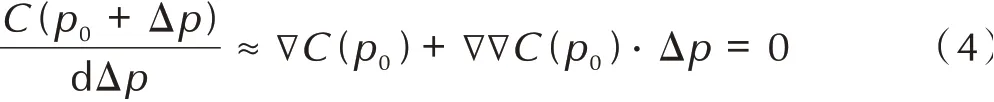
式中，P0为经整像素级别的搜索，获得的初始估计值；∇∇C(p0)为相关函数C（p）在初始估计值处的二次偏导，又称为Hessian 矩阵，可通过牛顿迭代得到方程解。

1.2 内聚力模型

粘接界面的本构关系采用双线性内聚力模型［5］，其依次为上升段、下降段和完全脱粘段，上升段和下降段均为线性假设［12］，如图2 所示。

图2 中，σmax为最大粘接强度，MPa，δe、δf分别为损伤起始位移、最大失效位移，mm。

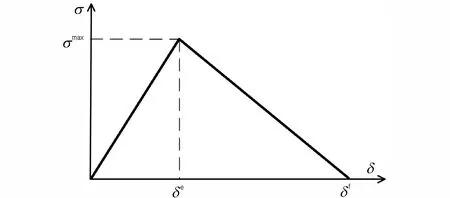
图2 双线性内聚力模型Fig.2 Bilinear cohesive zone model

粘性界面单元简化为仅考虑垂直界面的法向变形和沿界面方向的剪切变形，如图3 所示。

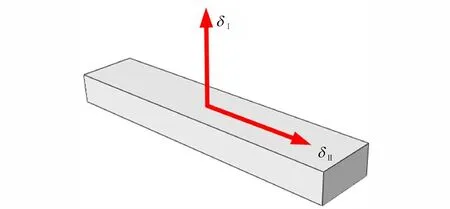
图3 界面单元变形示意图Fig.3 Deformation schematic diagramof interface element

δⅠ、δⅡ分别为沿界面方向的法向变形和剪切变形，mm。

单元的总变形，如式（5）：

式中，δm为单元的总变形，mm。

以损伤因子d表征界面损伤情况，损伤因子与界面损伤起始位移的关系，如式（9）：

可见，双线性内聚力模型的形状可由最大粘接强度、模量、失效断裂能所决定。为方便后续开展仿真计算，将粘性界面单元简化为各向同性，各物理量的法向、切向数值设置相同。

2 力学实验

2.1 矩形粘接试件拉伸实验

2.1.1 试件与实验过程

按 照QJ2038.1A-2004 标 准［21］的 固 体 火 箭 发 动机矩形粘接试件为研究对象，该试件由钢件、三元乙丙橡胶（EPDM）绝热层、端羟基聚丁二烯（HTPB）/异佛尔酮二异氰酸酯（IPDI）衬层、HTPB 推进剂组成，在下侧钢件与绝热层间的左右两端，预制了长度为20 mm的人工脱粘层，以达到缓解两端应力集中的目的。

DIC 技术要求变形体表面须具有丰富的特征，这些特征会对测量的精度有着重要的影响，随机散斑可提供足够的特征信息［15］，为了获得高对比度的随机散斑，实验前使用口径0.5 mm 的水性笔在推进剂表面绘制网格，网格尺寸大致为3.0 mm×1.3 mm。

采用位移加载方式，拉伸角度为0°、速率为5 mm·min-1，使用冷光源持续提供照明，CCD 相机拍摄频率为0.5 Hz，图像的分辨率为4000 pixel×3000 pixel，记录拉伸载荷与位移数据，直至拉伸实验结束。拉伸载荷与试件上表面的面积（2000 mm2）比值定义为拉伸应力σ，拉伸位移与试件高度（62 mm）比值定义为拉伸应变ε。

2.1.2 实验结果

粘接界面的面积相对较小，可获取的信息少且随机性强，因此采用推进剂本体区域的位移信息开展反演研究。同时，下侧钢件与绝热层两端，预制了长度为20 mm 的人工脱粘层，导致相对应的推进剂位移信息无法有效反映粘接界面的本构关系。因此以推进剂区域（20 mm≤x≤80 mm）作为ROI。

应力-应变曲线的加载段可大致分为3 个阶段：加载初期，粘接试件与夹具间存在缝隙，曲线存在一定的非线性，ROI 位移场受缝隙的影响较大，不利于采用该阶段的图像开展ROI 位移场分析；随后，曲线近似呈线性关系增长，界面发生了微小损伤，对试件的力学性能影响较小；达到一定载荷后，界面出现了不可逆损伤，曲线上升速率逐渐放缓，直至达到应力峰值。使用开源数字图像相关分析软件Ncorr［19］对CCD 相机拍摄的拉伸变形图片序列中的ROI 开展计算，选择二、三阶段对应的ε为0.05、0.08 拉伸状态开展ROI 位移场情况分析，如图4 所示。

两侧人工脱粘层尖端处产生应力集中现象，左侧人工脱粘层尖端处承载能力较右侧弱，ε为0.05 时，左侧人工脱粘层尖端处出现微裂纹，ε为0.08 时，左侧人工脱粘层尖端处的裂纹已大幅度向右扩展。ROI 沿x方向的变形程度小，图4a、图4b 中沿x方向的位移呈近似对称分布，受左侧人工脱粘层尖端处的微裂纹影响不明显。0°拉伸条件下，试件主要在y方向上产生变形，ε为0.05 时，左侧推进剂沿y方向的位移略高于右侧，图4c 中沿y方向的位移不呈对称分布，ε为0.08时，左侧推进剂沿y方向的位移明显高于右侧，图4d中的红色（沿y方向位移较小）区域向右下侧偏移明显。

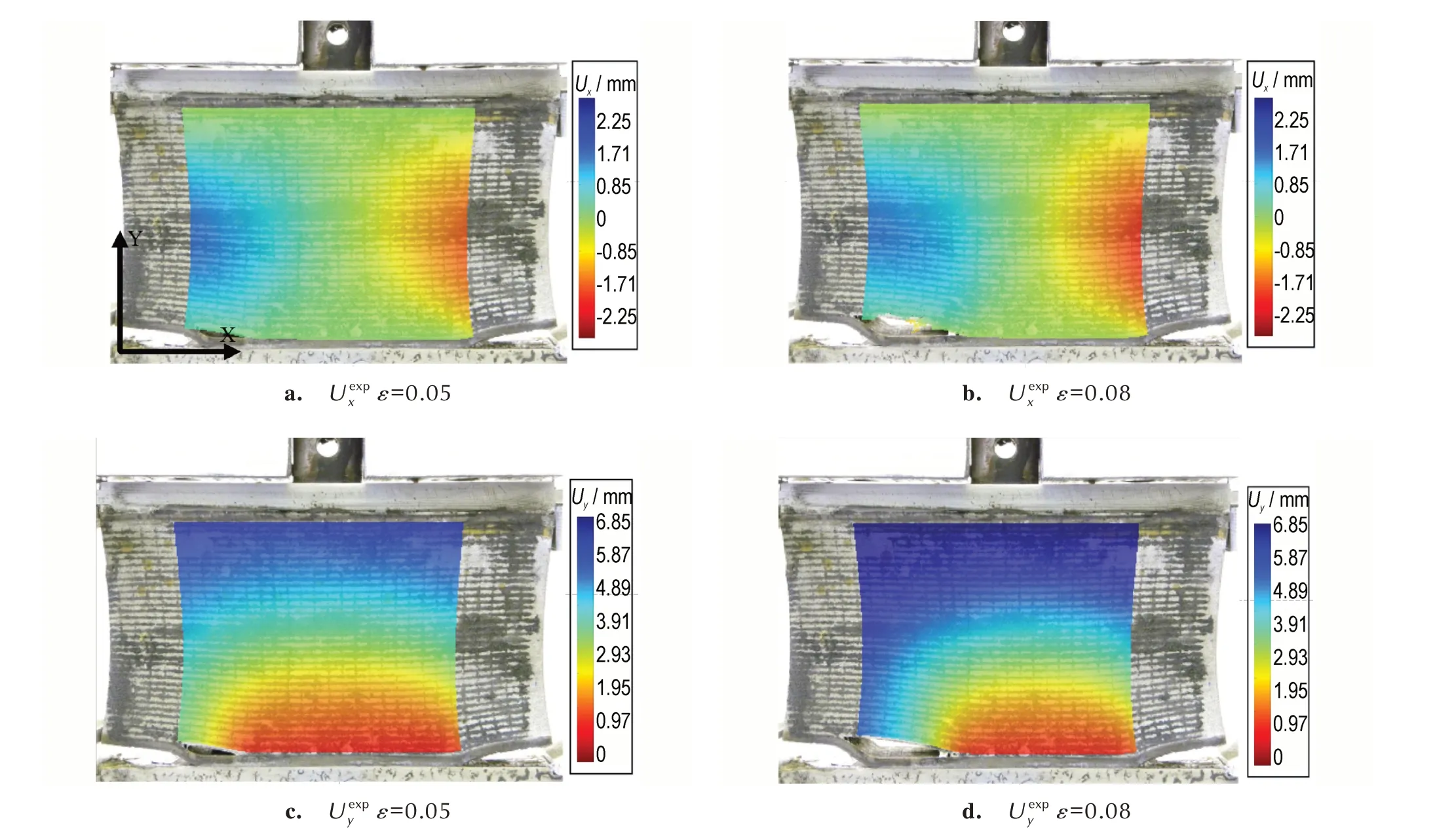
图4 推进剂区域（20 mm≤x≤80 mm）的位移云图Fig.4 Displacement cloud diagrams of propellant region（20 mm≤x≤80 mm）

2.2 HTPB 推进剂松弛实验

2.2.1 试件与实验过程

按 照QJ2487-1993 标 准［22］的HTPB 推 进 剂 试 件为研究对象。在室温20 ℃条件下，对其开展松弛实验，如图5 所示。

图5 HTPB 推进剂试件与夹具安装装置Fig.5 HTPB propellant specimen and fixture installation device

2.2.2 实验结果

HTPB 推进剂的松弛模量可以由Prony 级数表示［5］，如式（11）：

式中，E∞为平衡模量，MPa。采用最小二乘法对实验得到的松弛曲线进行拟合，拟合后的推进剂松弛曲线，如图6 所示，得到7 级Prony 级数的各项参数，见表1。

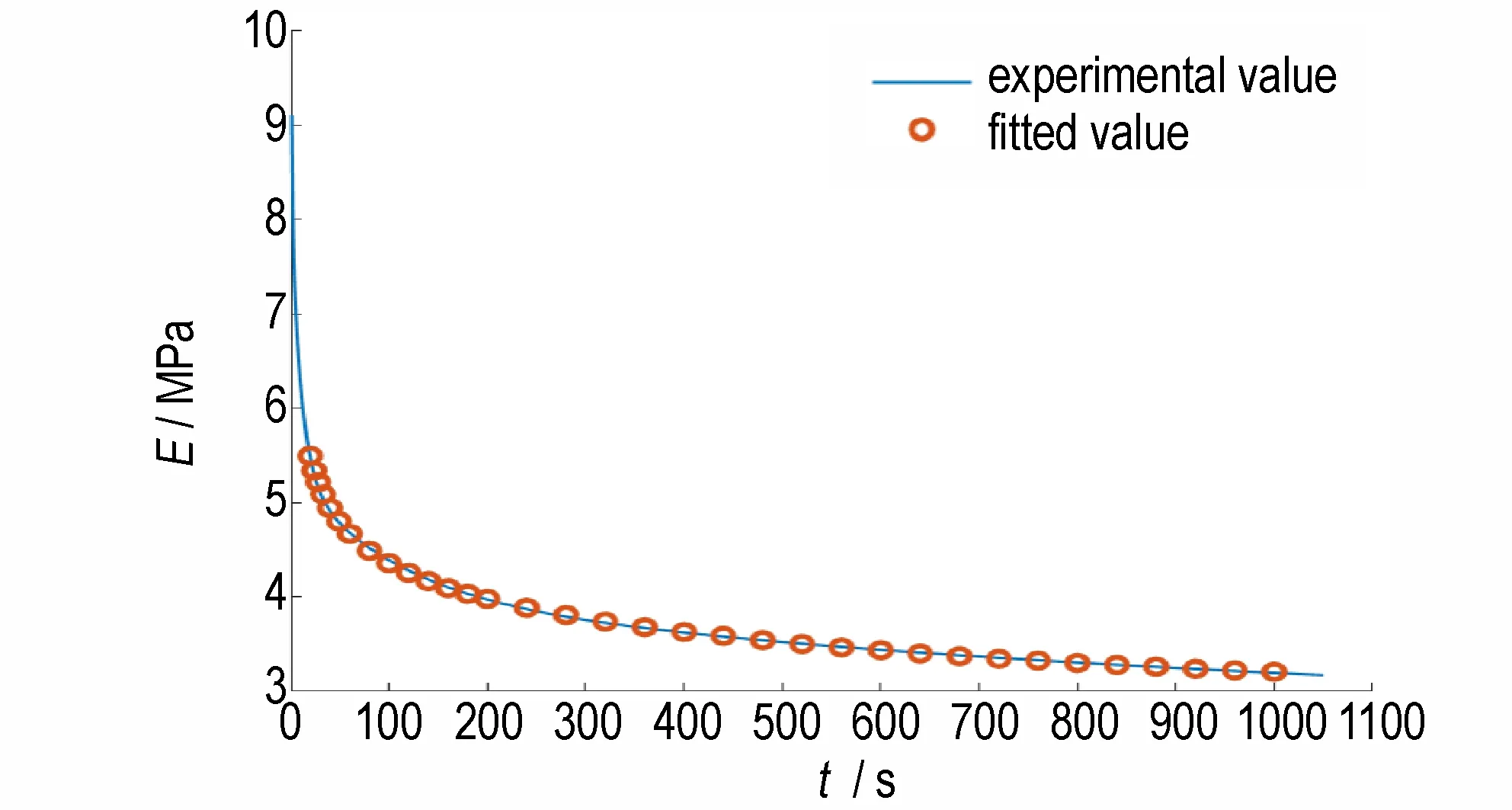
图6 拟合后的推进剂松弛模量曲线Fig.6 The relaxation modulus curve of propellant after fitting

表1 推进剂Prony 级数参数Table 1 Prony parameters of propellant

3 反演识别与效果分析

3.1 反演识别

在仿真过程中，粘接界面各处的本构关系简化一致，两侧人工脱粘层尖端处的破坏程度相同；而对矩形粘接试件的拉伸实验中，其通常表现为单侧起裂。在图4 中发现，ε＞0.08 时，左侧的人工脱粘层尖端处脱粘严重，位移云图不再呈对称分布，若仍以整个拉伸过程中的ROI 位移信息构建目标函数，则会导致反演精度低。因此采用ROI 位移场信息与应力-应变曲线数据信息共同构造目标函数的方法降低误差：0≤ε≤0.105 的 实 测 数 据 信 息 采 用ε为0.05、0.08 的 位 移 场信息进行表征，0.105＜ε≤0.152 的实测数据信息采用应力-应变曲线（0.105≤ε≤0.152）数据信息进行表征。研究采用Hooke-Jeeves 优化算法逐步修正待求参数，反演流程如图7 所示。主要包括有限元模型的建立、目标函数的构造、内聚力模型参数迭代更新3 部分。

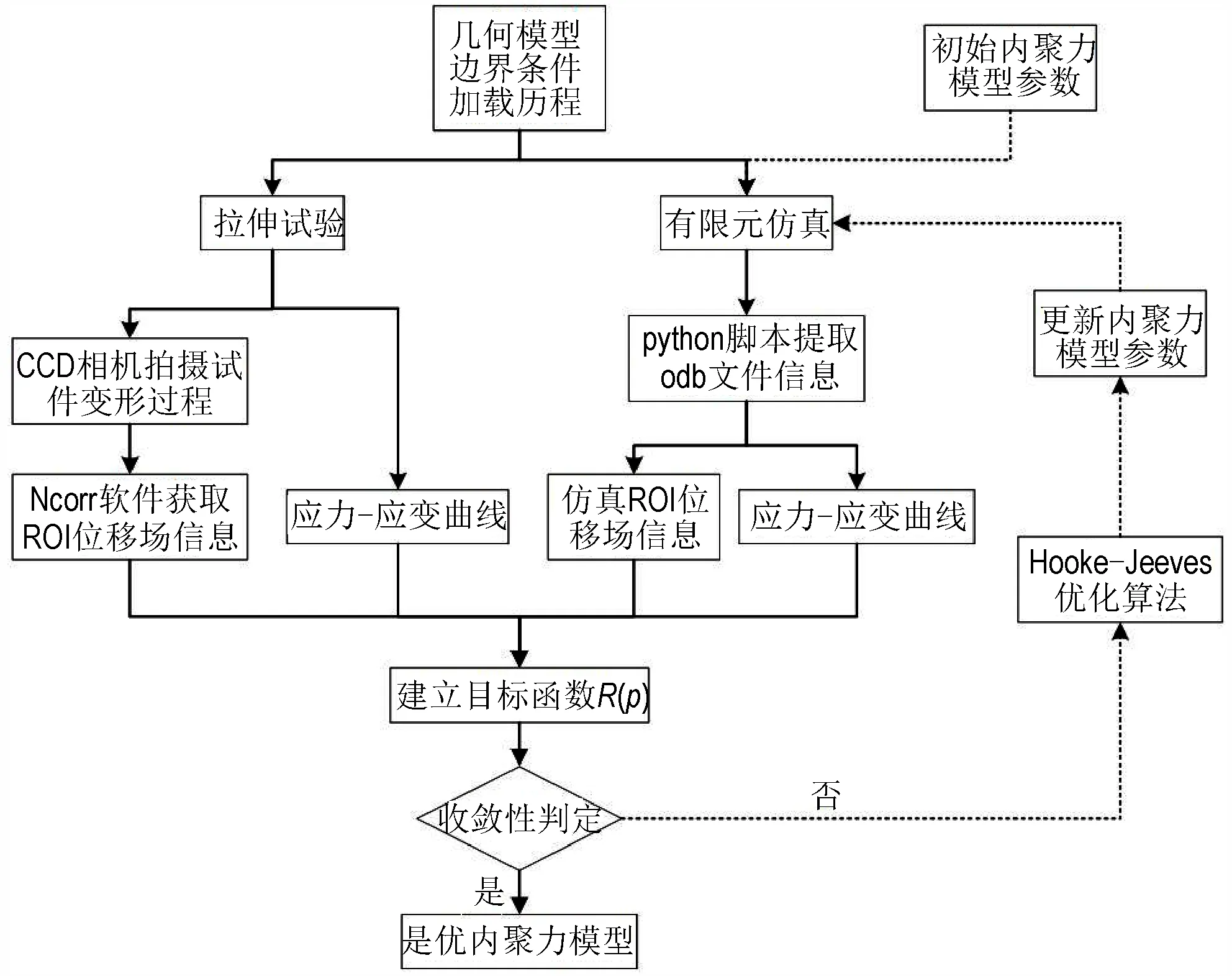
图7 反演流程图Fig.7 Inversion flow chart

（1）有限元模型的建立

按照矩形粘接试件的结构和尺寸建立有限元模型，其中推进剂、绝热层网格的单元类型为C3D8H，钢件网格的单元类型为C3D8，衬层网格的单元类型为COH3D8，模型中共2556 个节点，如图8 所示。

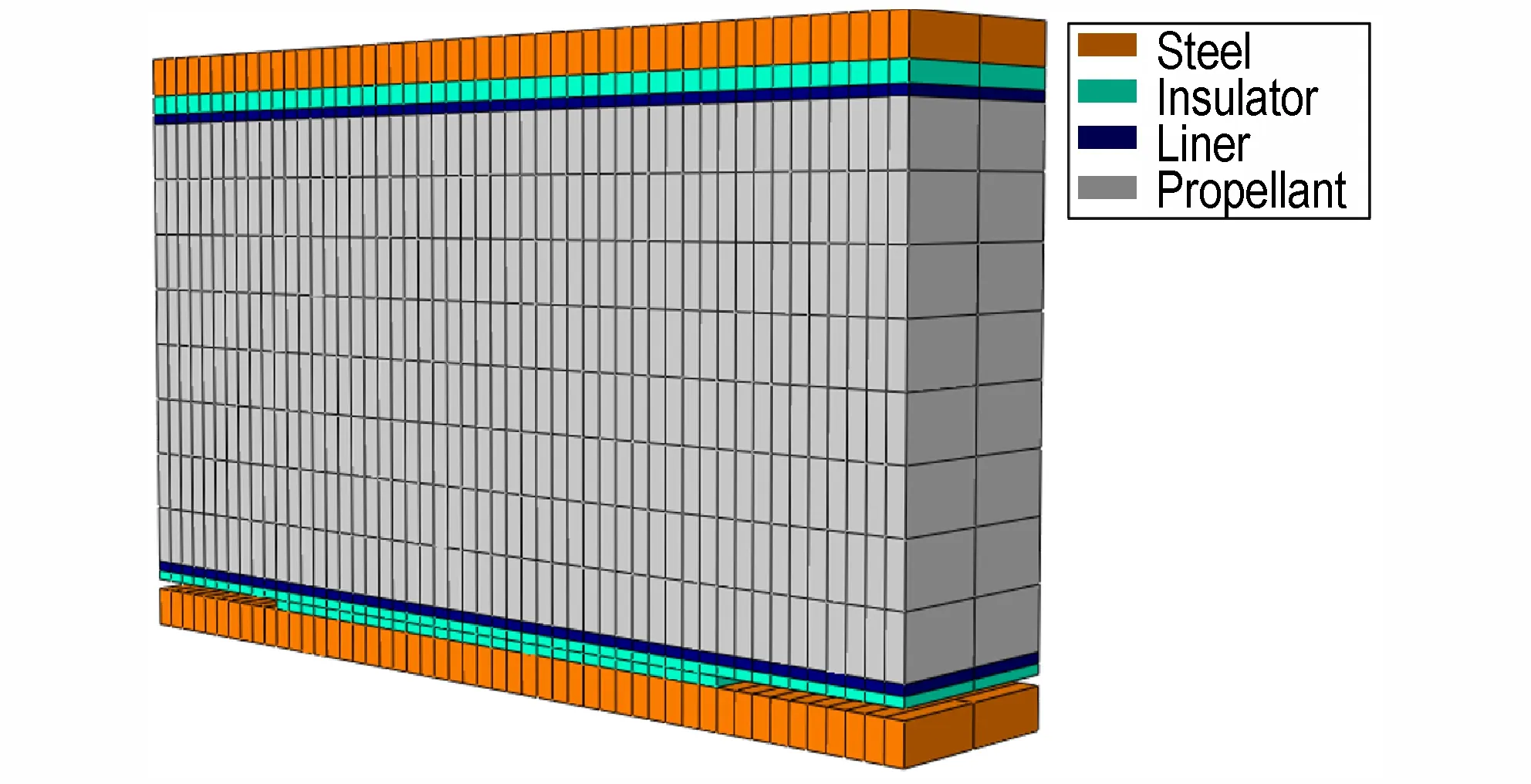
图8 有限元模型Fig.8 Finite element model

绝热层和钢件在拉伸实验中的变形小，视为线弹性材料，其力学性能参数见表2。

表2 力学性能参数［5］Table 2 Mechanical properties parameters

HTPB 推进剂为粘弹性材料，其松弛模量可以由Prony 级数表示，采用2.2 节的松弛实验数据。

（2）目标函数的构造

Hooke-Jeeves 优化算法由目标函数探索设计空间，通过目标函数表征仿真结果与实测结果的相近程度，数值越小，则表明二者越接近。设置相同时间间隔对仿真、实测应力-应变曲线进行离散，进而构造目标函数R（p），如式（12）：

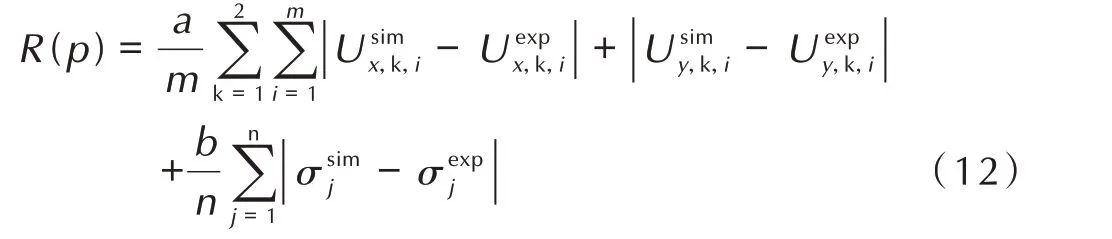
式中，p为内聚力模型相关参数组成的向量集合；U为位移，mm；x、y分别为沿界面平行、垂直的方向；a、b为放大/缩减因子；m、n分别为ROI 位移场与应力-应变曲线目标点的数量；i、j为目标点的编号；sim、exp 代表仿真情况与实测情况；k 表示拉伸状态（ε=0.05、0.08）。

（3）内聚力模型参数迭代更新

在试算时发现：最大粘接强度影响应力-应变曲线的峰值、模量影响曲线的上升段、失效断裂能影响曲线的下降段。经有限元试算工作，确定最大粘接强度、模量、失效断裂能的初值，如表3 所示。

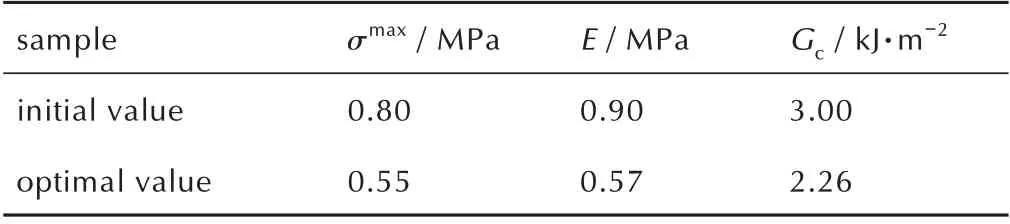
表3 相关参数的初值与最优值Table 3 Initial and optimal values of relevant parameters

Hooke-Jeeves 优化算法的初始步长为0.05，阈值为0.01，缩减因子为0.5，步长加速因子为1.1，目标函数阈值设为2.5。反演过程中，相关参数以及目标函数的变化情况，如图9 所示。

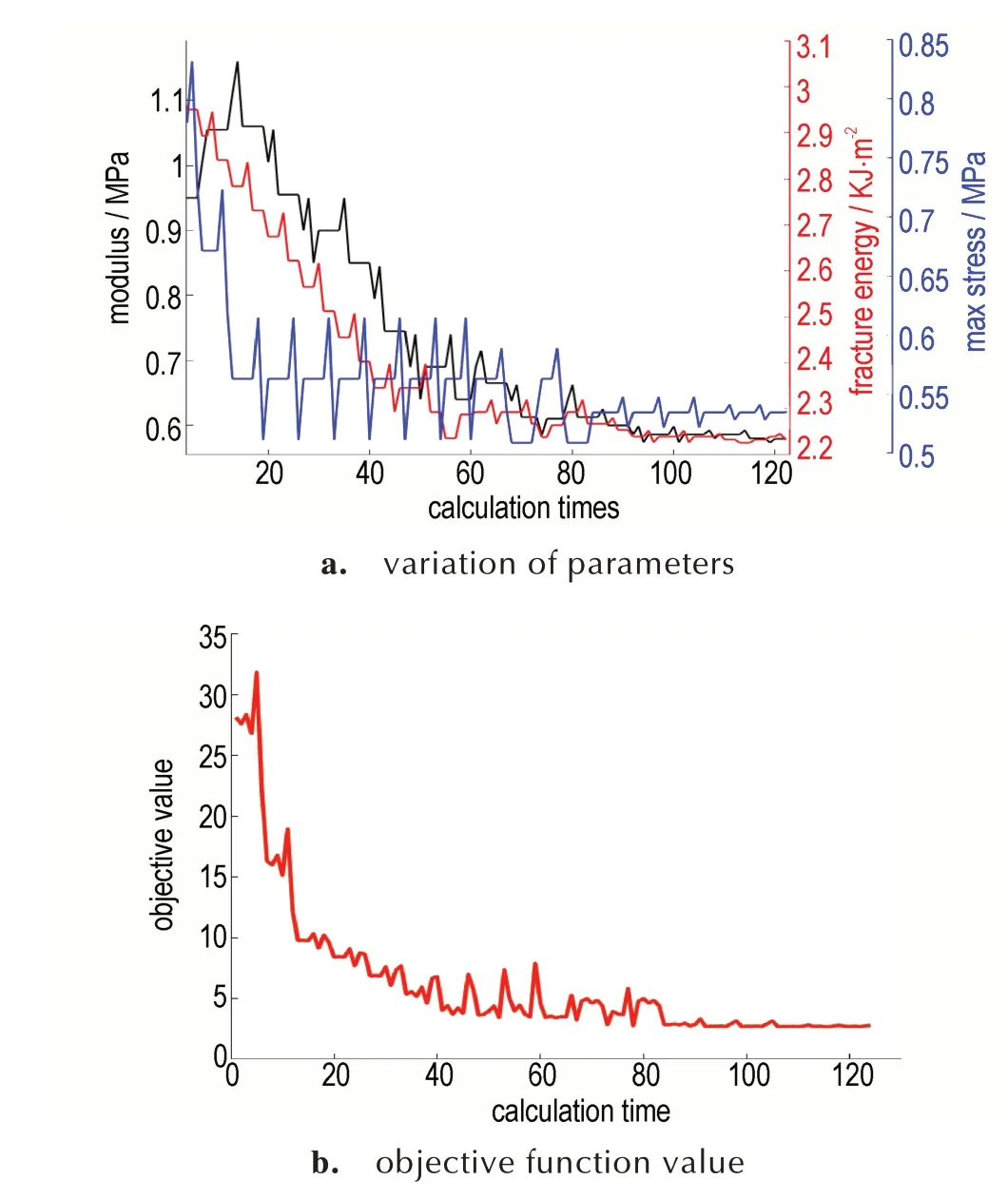
图9 相关参数与目标函数的变化情况Fig.9 Changes of relevant parameters and objective function

反演过程共开展19 轮“探测移动”，合计124 次计算。最终，增量步长缩减为6.25×10-3，小于设定的步长阈值。目标函数曲线在第85 次计算后基本保持平稳，收敛情况较好，在第116 次赋值试算中的目标函数值最小，表明该组参数下的仿真结果与实测结果最为接近，即最优值，如表3 所示。

3.2 反演效果分析

基于3.1 节的反演识别工作，获取了表征粘接界面力学性能的最优双线性内聚力模型。需通过与相应的实验数据进行对比，从而分析最优双线性内聚力模型的准确性。通过单向拉伸过程中的应力-应变曲线信息和ROI 位移误差云图信息，对最优双线性内聚力模型的准确性展开分析。

基于初始双线性内聚力模型和最优双线性内聚力模型开展仿真计算，相对应的仿真应力-应变曲线以及实测应力-应变曲线，如图10a 所示。初始双线性内聚力模型和最优双线性内聚力模型的应力数据与实测应力数据的比值变化图，如图10b 所示。

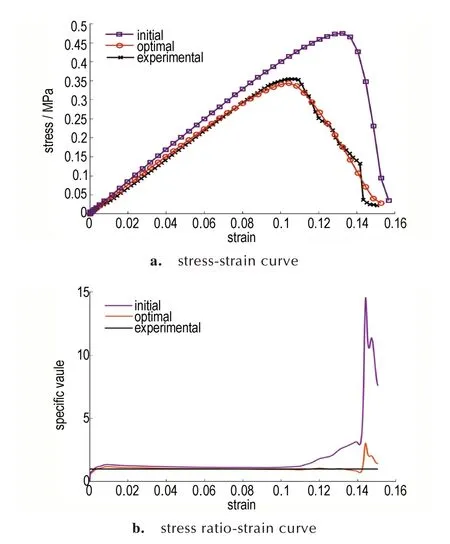
图10 仿真和实测应力-应变相关曲线Fig. 10 Simulated and measured stress-strain correlation curves

图10a中，初始应力-应变曲线的上升斜率与实验曲线的差距较小，但在整个拉伸过程中，应力数据普遍高于实测数据，可见，初始双线性内聚力模型并不能有效的表征粘接界面的真实力学性能。最优双线性内聚力模型的应力-应变曲线与实测曲线具有相同的变化趋势与规律，相似度较高。图10b中，在拉伸阶段（0≤ε＜0.11）时，初始与最优的应力数据比值均近似为1；在拉伸阶段（0.11≤ε＜0.15）时，初始应力数据比值大幅度提高，最大值达到14.6；在拉伸阶段（0.11≤ε＜0.14）时，最优的应力数据比值近似为1，在拉伸阶段（0.14≤ε＜0.15）时，最大比值仅为3.0。

以相对误差r反映仿真、实测应力-应变曲线的相近程度，如式（13）：

式中，s为应力-应变曲线与横坐标轴围成的面积，MPa。

初始曲线的相对误差为44.7%，最优曲线的相对误差降低为4.3%。可见，该反演识别方法可以对内聚力模型进行有效修正，反演效果理想。

ε为0.05、0.08 拉伸状态下的仿真位移云图，如图11 所示。

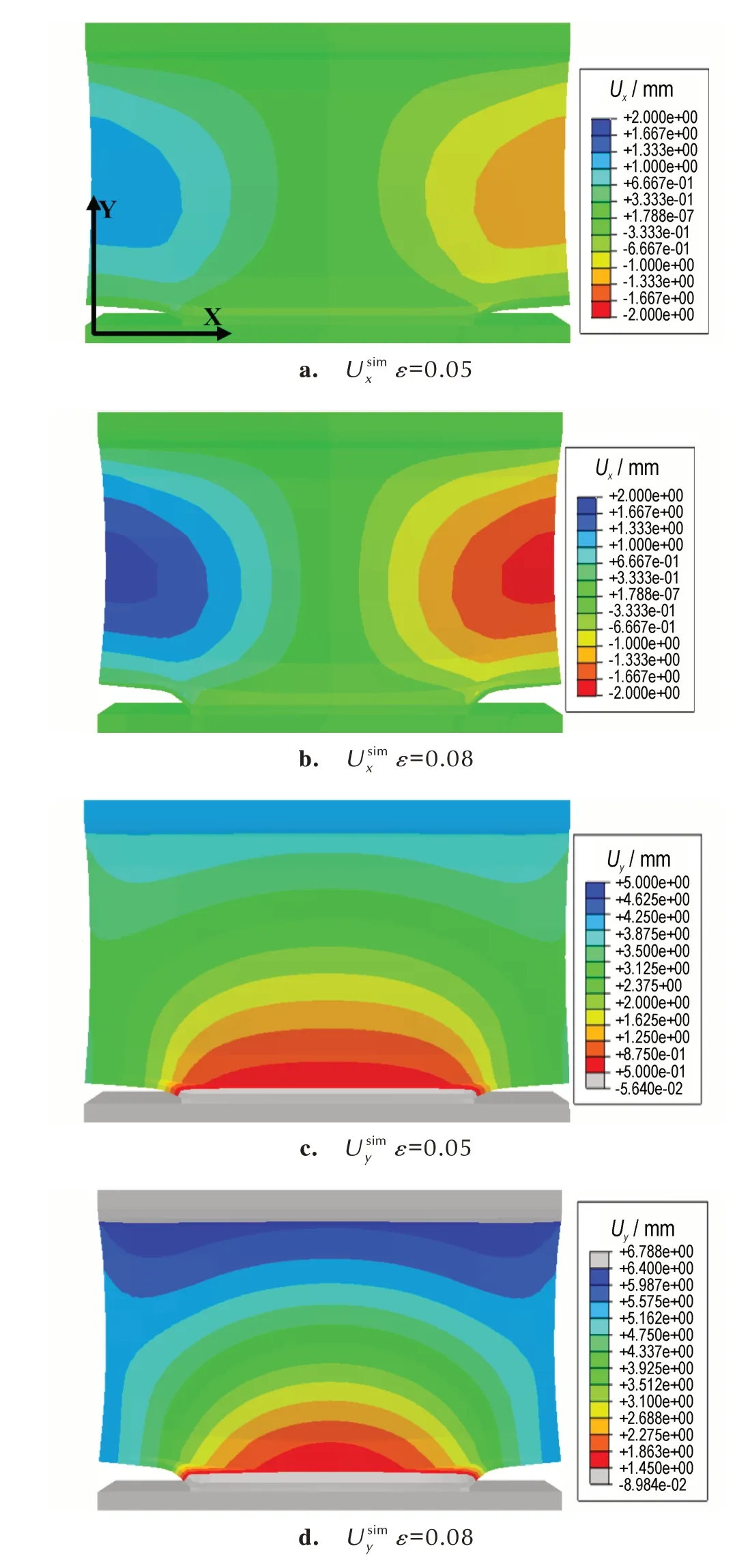
图11 仿真位移云图Fig.11 Simulation displacement cloud images

在仿真过程中，由于将粘接界面各处的本构关系简化一致，两侧人工脱粘层尖端处的损伤情况相同，并且沿x、y方向的仿真位移云图均呈对称分布，与实测位移云图的分布特征均基本一致。ε为0.05 时，两侧的人工脱粘层尖端已大幅度沿拉伸方向运动，粘接界面附近区域沿y方向大致进行了0.5 mm 位移，两侧的人工脱粘层有效的缓解应力集中现象的发生。ε为0.08时，粘接界面附近区域沿y 方向大致发生了1.4 mm 位移，此时粘接界面损伤严重。

以绝对误差r′反映仿真、实测ROI 位移场的相近程度，如式（14）。ROI 位移误差云图，如图12 所示。

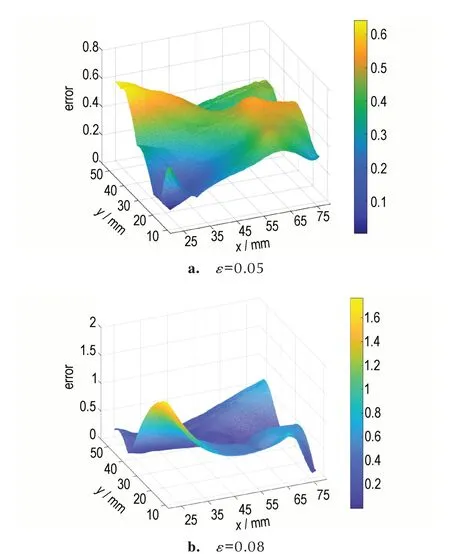
图12 ROI 位移误差云图Fig.12 Cloud maps of ROI displacement error

ε为0.05 时，ROI 位 移 误 差 云 图 的 最 大 误 差 为0.64 mm、平均误差为0.38 mm，其误差分布相对均匀。ε为0.08 时，ROI 位移误差云图的最大误差为1.76 mm、平均误差为0.45 mm，上半区域（7≤y≤31）的误差相对较小，且误差分布相对均匀，由左侧的人工脱粘层处最先发生破坏，导致ROI 位移误差云图中下半区域（31＜y≤55）左侧的误差相对较大。

以上分析均表明采用反演方法获取的双线性内聚力模型可以用于表征粘接界面的真实本构关系。

经分析，误差主要来源于5 方面：1、推进剂实际本构关系复杂，对于拉伸载荷较大时，推进剂所采用本构参数不能完全表征其真实的力学性能，一定程度上影响了反演精度；2、对钢件和绝热层的力学性能予以简化处理，通过引用相关文献的方式确定二者的力学性能参数，会与实际的力学性能存在偏差，但较第一条误差来源相比占次要因素；3、试件表面不平整，同时，CCD 相机在拍摄过程中，各图片的亮度和对比度很难保证完全一致等因素，会影响图片的灰度分布，进而影响位移场测量结果。4、仿真过程中，粘接界面作简化处理，各处的本构关系一致，而在矩形粘接试件的拉伸实验中，其通常为单侧起裂，粘接界面两侧的力学性能实际不完全相同。5、可通过适当增加其他拉伸状态下的位移场信息的方式，丰富拉伸阶段（0≤ε≤0.105）中的实测数据信息，以达到更好的表征的效果。

4 结论

（1）基于DIC 技术与Hooke-Jeeves 优化算法相结合的反演识别方法，可以准确地获取固体火箭发动机粘接界面模型，拉伸速率为5 mm·min-1时，双线性内聚力模型的最大粘接强度、模量、失效断裂能分别为0.55 MPa、0.57 MPa、2.26 kJ·m-2。

（2）仿真与实测应力-应变曲线的相对误差由初始44.7%修正为4.3%，拉伸应变为0.05、0.08 状态下的ROI 最大位移误差分别为0.64 mm、1.76 mm，平均位移误差分别为0.38 mm、0.45 mm，均表明所采用的反演识别方法的精度较高，建立的双线性内聚力模型可以一定程度上表征粘接界面的真实本构关系。

（3）本研究为粘接界面模型的精准获取提供了一个新的思路，并对粘接界面的力学行为分析提供理论基础和参考依据。在后续工作中，通过对五点误差来源方式加以改进，会使反演精度有效提高。