滑坡体散体化对涌浪波动特征的影响

郑飞东,王平义,李 云

(1. 重庆交通大学河海学院,重庆 400074；2. 南京水利科学研究院,江苏 南京 210029)

全世界有超过一半的大型河流系统因被大坝拦截而形成河道型水库[1]。在大坝运行期间,水库水位的骤然涨落会引起库区边坡的变形和失稳,严重时将诱发水库滑坡地质灾害和次生涌浪灾害[2]。涌浪在传播过程中不仅会对船舶、航道整治建筑物及库区大坝施加较大的冲击荷载,威胁船舶安全和工程结构物的稳定性,而且会对沿岸岸坡产生强烈的冲刷,影响其稳定性,涌浪一旦爬升冲上陆地,还会对沿岸居民的人身安全造成极大威胁[3- 7]。因此,相对于滑坡灾害本身而言,次生的涌浪灾害带来的危害和损失更大[8],对其开展理论和技术研究具有重要意义。

根据滑坡体物质的组成,滑坡体兴波的类型主要可分为岩质滑坡兴波和土质滑坡兴波2类。国内外专家学者针对滑坡涌浪的波动特性开展了大量的研究工作,并取得了丰硕的成果。由于流固耦合动力学过程和自由面大变形物理学过程非常复杂,滑坡涌浪的理论研究通常建立在一系列简化和假设的基础上[9- 15],导致这些研究成果并不能充分反映流固耦合效应对涌浪发育的影响机制。在岩质滑坡兴波模型试验和数值模拟研究方面,已有研究通常在将滑坡体视作刚性块体的基础上,探讨了静水深、滑动面倾角、滑坡体尺寸及形状、滑坡体入水速度等参数对兴波幅值以及沿程波高分布规律的影响作用,如Ataie- Ashtiani等[16]、岳书波等[17]、Heller等[18]。对于土质滑坡兴波,研究者们大多采用尺寸均匀的小球[19- 21]或圆柱体[22- 26]对滑坡体进行模拟,主要分析了涌浪的波动参数对滑坡体相对厚度、滑动弗劳德数、冲击参数及相对质量等量纲一控制参数的定量响应规律。然而对于河道型水库中常见的岩质滑坡,滑坡体在滑动过程中会发生散体化,进而分解成形状及大小各异的块体,与已有研究简化的滑坡体模型有显著差异。由于块体堆积体滑坡兴波的影响因素众多且作用关系复杂,使得对这一流固耦合问题进行研究的难度很大。

本文通过开展三维水池物理模型试验,探讨滑坡体的散体化对涌浪波动特性的影响作用,相关成果可为全面揭示块体堆积体滑坡兴波机制提供一定的技术指导和理论支撑。

1 试验装置及方法

滑坡体散体化试验在横断面为梯形的三维水池中进行,其顶宽为8.00 m,底宽为2.94 m,深度为1.16 m。试验模型布置示意图见图1。滑坡发生装置设置在水池的左岸,主要由滑架、滑槽、闸门及3个倒链葫芦构成,其中滑槽的最大尺寸为2.0 m×1.6 m×0.7 m(长×宽×高)。试验通过操作起重葫芦来调节滑槽底板与水池底板之间的角度；通过快速抽出安装于滑槽尾端附近的平板闸门释放滑坡体,以模拟其沿滑坡面的滑动过程以及该过程中滑坡体的散体化过程。本文试验条件下滑坡面与静水面的夹角α=40°,水池的静水深d0=0.505 m。本文采用直角坐标系xoz,原点o位于滑坡面与静水面交线的中心,垂直向上为z轴正向,滑坡体滑动方向为x轴正向。

试验采用西南水运科学研究所研发的无线数字波高仪对涌浪形成后水面的波动进行测量,其量程为0～60 cm,精度为±0.1 cm,数据采集频率设置为145 Hz。试验中,沿x轴方向按相邻波高仪间距Δx=0.2 m共布置9根波高仪,其中G1波高仪安装在x=1.0 m的位置(x/d0=1.98),用于获取初生涌浪的形态特征；G2—G9波高仪布置在x=1.2～2.6 m之间,以量测涌浪沿x方向传播过程中的变化。

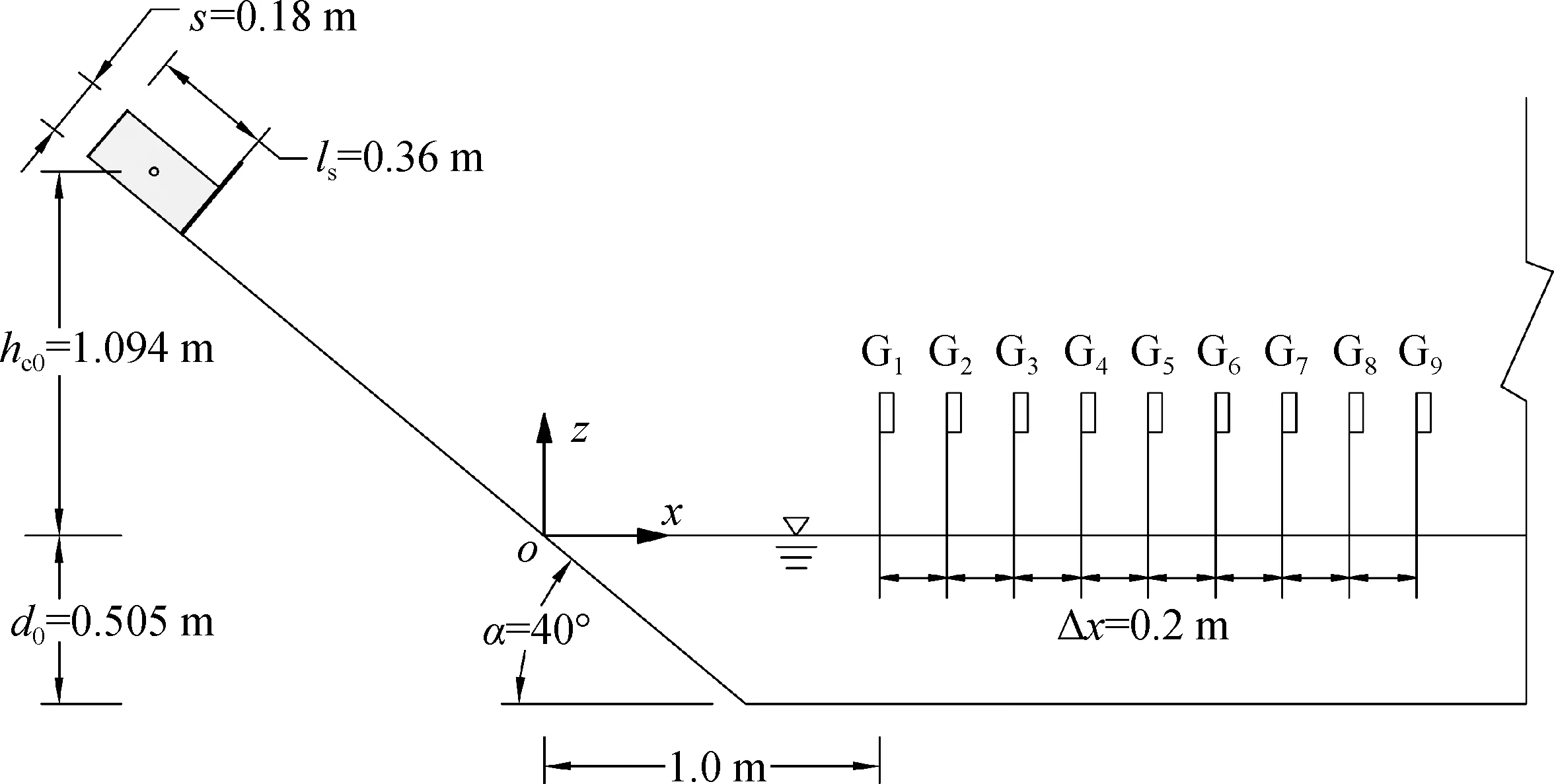
图1 试验模型布置示意Fig.1 Schematic of the experimental facility

试验共研究了4种滑坡体模型入水兴波过程,分别为模型A1、A2、A3和A4。模型A1为一刚性块体,模型A2、A3和A4分别为由不同尺寸的刚性均匀长方体(长∶宽∶高=3∶2∶1)堆积而成的组合体,详情见图2和表1。4种滑坡体模型的总尺寸相同,为0.36 m×0.36 m×0.18 m(ls×bs×s)。滑坡体模型所采用的刚性块体由水泥和砂浆制作而成,密度为2 500 kg/m3。滑坡体在释放前,其质心距离静水面的高度hc0=1.094 m。

图2 滑坡体模型照片Fig.2 Photograph of landslides

表1 滑坡体模型关键参数

已有研究结果表明[27],初生涌浪的波动特征与hc0和滑坡体与滑槽之间的动摩擦系数(μs)有关,后者可通过进行单一块体的滑动试验采用下式进行估算：

(1)

式中：Sa为块体沿滑槽的滑行距离,m;g为重力加速度,m2/s；ta为块体的滑行时间,s。根据本研究的试验结果,μs=0.40。为便于下文定量分析滑坡体散体化程度对初生涌浪的影响,定义滑坡体模型的离散度：

Rd=-ln(1/Ns)

(2)

当Rd=0时代表滑坡体下滑过程中不发生散体化；离散度偏离0的程度越大,滑坡体的散体化程度越高。

2 结果与讨论

2.1 波面变化过程

图3 滑坡体A1兴波条件下特征测点处的波面变化Fig.3 Wave profiles at several locations of landslide A1

不同滑坡体入水都产生了具有正振幅先导波的振荡波场,但波动的变化幅度和周期有所差异。Miller等[20]在二维水槽中对涌浪波形的演化过程进行了研究,指出先导波波面在传播过程中会逐渐趋近孤立波。为了便于与孤立波进行对比,将孤立波的一阶理论波面绘制于图3和图4中(点线)。从图3和图4中可以看到,与相同波幅的孤立波比较,先导波的波长、周期均显著小于孤立波。造成这种不同的原因可能与涌浪的传播方向受限有关：三维条件下涌浪以滑落点为中心向周围的自由水域传播;而在二维条件下,由于受到水槽侧壁的约束,涌浪仅沿滑坡体的运动方向演进。

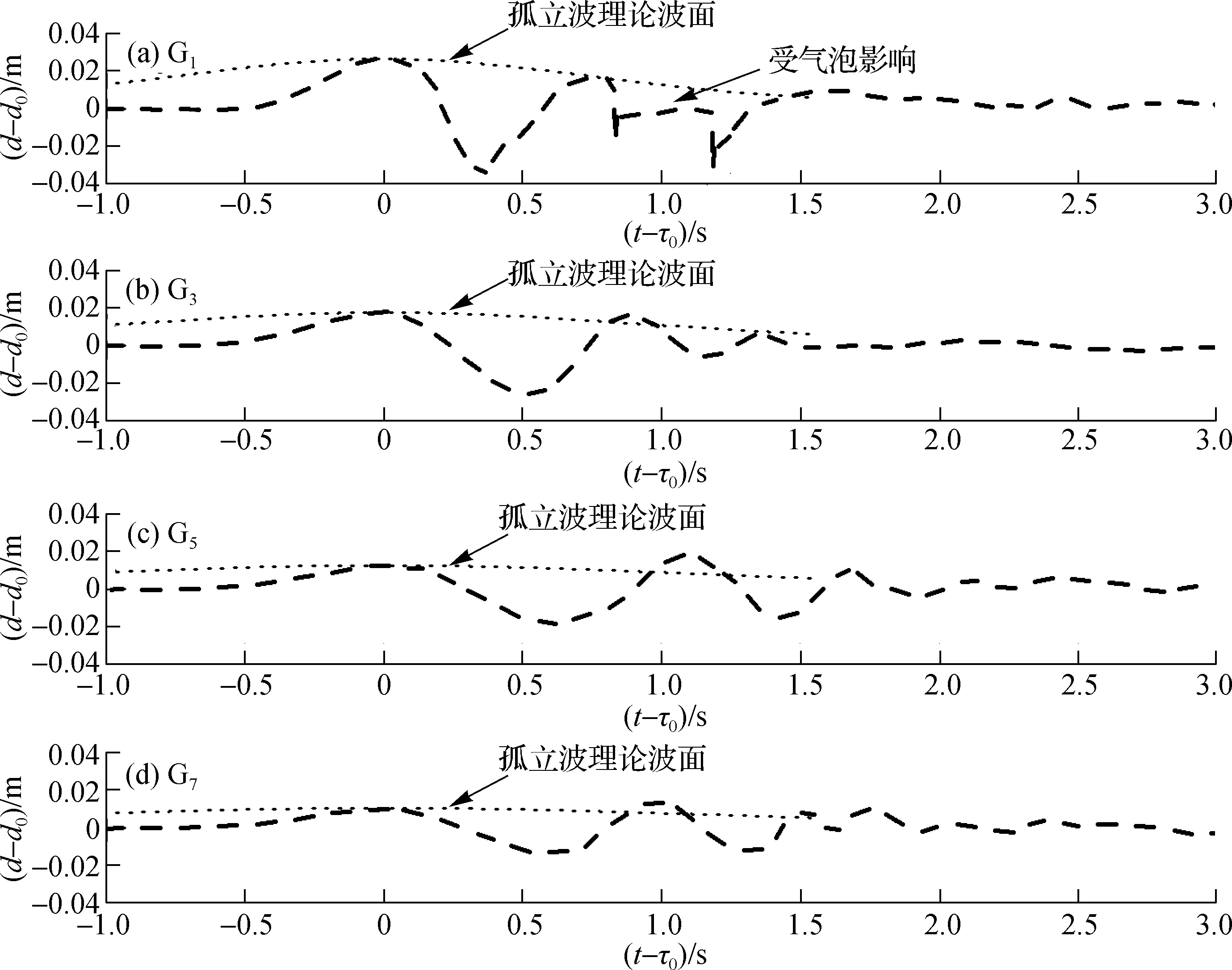
图4 滑坡体A2兴波条件下特征测点处的波面变化Fig.4 Wave profiles at several locations of landslide A2

2.2 初生涌浪最大波幅和最大波高

最大波峰幅值(am)和最大波高(Hm)是初生涌浪最重要的波动参数。本文参照前人的做法[25],将最大波高定义在波列中最大波峰幅值出现的位置。根据试验结果,当初生涌浪波列依次通过测点G1—G9时,am为某测点处先导波的波峰幅值,因此定义Hm为该测点处第一波峰顶与第一波谷底的水深差。表2给出了不同滑坡体入水兴波时初生涌浪的最大波幅和最大波高。Huang等[27]在三维水池中对滑坡兴波问题进行了试验研究,结果表明单一块体和块体堆积体滑坡兴波时初生涌浪的最大波幅可分别采用式(3)和式(4)计算。

(3)

(4)

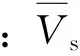
表2 初生涌浪的最大波幅和最大波高

图5给出了最大相对波幅和最大相对波高随滑坡体离散度的变化情况,其中下标A1指的是滑坡体模型A1。由图5可知,初生涌浪的最大波幅和最大波高均随Rd的增大而减小,这与预期的结果相符。当Rd由0(滑坡体A1)增至2.89(滑坡体A2)时,最大波幅的减小幅度为未发生散体化时的27%；当Rd> 2.89时,滑坡体的散体化程度变化对最大波幅无明显影响。相比而言,当Rd由0增至4.97(滑坡体A3)时,初生涌浪最大相对波高(Hm/d0)迅速由0.156减小为0.093,减小幅度达40%；随着Rd进一步增加,最大波高基本不发生变化。

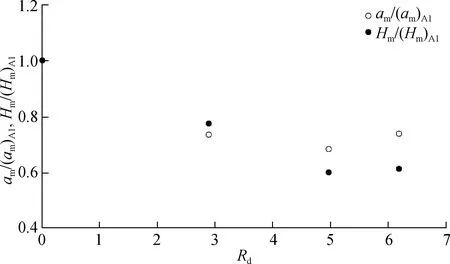
图5 最大相对波幅和最大相对波高随离散度变化Fig.5 Maximum relative wave amplitude and maximum relative wave height as functions of Rd

2.3 涌浪波幅和波高的沿程变化

图6给出了试验条件下第一波峰相对波幅(a1c/d0)和第二波峰相对波幅(a2c/d0)的沿程变化情况。从图6中可以看到,在滑坡体入水点附近区域(如G1、G2、G3位置),各测点处第一波峰的幅值较第二波峰要大；随着涌浪向远场传播,第二波峰幅值与第一波峰幅值之间的差异逐渐减小,并最终超过第一波峰幅值。造成这种变化的原因与涌浪的传播持续受到耗散和色散效应共同作用有关[23],导致a1c/d0沿程的衰减速率明显高于a2c/d0,这与Huang等[27]的研究结果一致。

设初生涌浪最大波幅出现的测点位置为x=x0,那么有(a1c)x=x0=am。采用初生涌浪最大波峰幅值将第一波峰幅值量纲一化,结果见图7。需要说明的是,当滑坡体A1入水兴波时,测点G2处的a1c较G1有小幅的增加(见图6(a)),这与其他滑坡体兴波时的结果不同。因此,此处仅对第一波峰幅值达到最大值后的变化规律进行分析。从图7中可以看出,在初生涌浪向远区传播的过程中,受耗散和色散效应的共同作用,第一波峰幅值呈现出明显的衰减趋势,并且其衰减速度逐渐减小。Heller等[25,28]在二维水槽中对块体和散体滑坡兴波进行了研究,提出了沿程波幅的计算方法,见图7中实线和虚线。由图7可知,三维水池中涌浪先导波波幅沿滑动方向的衰减速度较二维水槽中的速度更快。

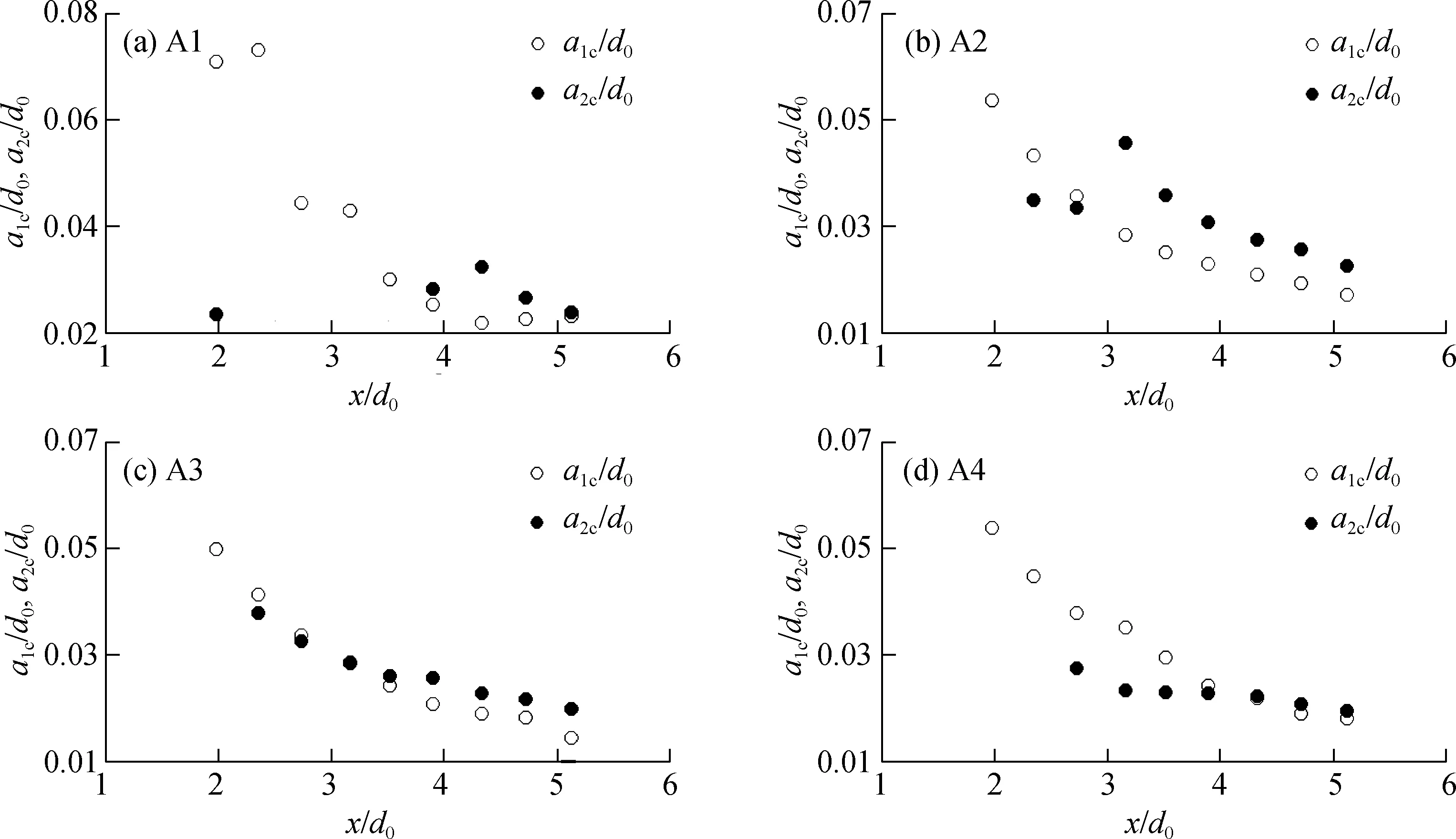
图6 涌浪第一、第二波峰幅值沿程变化情况Fig.6 Evolutions of the first and second wave crest amplitudes over propagation distance

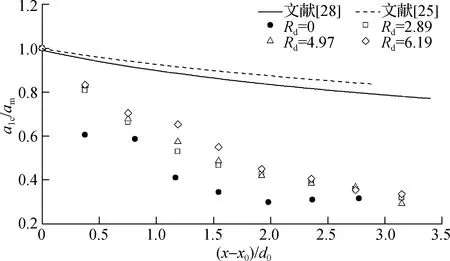
图7 a1c/am随(x-x0)/d0变化Fig.7 Variation of a1c/am with (x-x0)/d0

涌浪先导波作用下水质点仅在波动传播的方向上移动,这与孤立波非常相似[18]。因此,本文采用类比孤立波的方法对涌浪先导波的沿程波幅进行分析。Ippen等[29]系统研究了壁面糙率对孤立波波高衰减规律的影响,并给出了沿程波高的预测方法：

(5)

式中：f为Darcy- Weisbach糙率系数。

图8给出了a1c/am随量纲一传播距离(x-x0)/am的变化情况。从图8中可以看到,当滑坡体以散体块的形式入水兴波时,第一波峰幅值的沿程变化规律与Ippen等[29]提出的预测模型吻合良好,相应的f=0.25(图8中虚线,R2=0.99);相比而言,单块刚性体入水兴波时,第一波峰幅值的沿程变化与上述预测模型的一致性较散体块滑坡模型有所下降(图8中实线,R2=0.96),此时f=0.61。值得注意的是,块体堆积体作用下涌浪第一波峰的最大波幅十分接近(am/d0=0.050+7%),并且显著小于单块刚性体滑坡兴波的最大波幅。由此可知,先导波的最大波幅对a1c/am的沿程衰减过程影响显著,并且am/d0越大,a1c/am的衰减速度越快。需要说明的是,公式(5)为Ippen等[29]针对孤立波提出的沿程波幅预测模型,由于此时水波的色散效应与非线性效应相互平衡,波幅或波高的衰减是由边壁耗散造成的。然而在本文的试验条件下,涌浪波的色散效应与非线性效应无法达到平衡,并且涌浪的非线性很弱(am/d0<0.1),因而波幅或波高的衰减主要是色散和耗散共同作用的结果,此时f表征了色散和耗散2部分对波幅或波高沿程衰减影响的程度。

图8 a1c/am随(x-x0)/am变化Fig.8 a1c/am as a function of (x-x0)/am

图9 H1ct/Hm随(x-x0)/d0变化Fig.9 Variation of H1ct/Hm with (x-x0)/d0

对于任一测点处的波面过程,定义第一波高(H1ct)为第一波峰顶与第一波谷底的水深差。为了与前文的研究保持一致,对于滑坡体A1入水兴波工况,仅对G2—G9测点处的数据进行分析。需要特别注意的是,试验条件下最大第一波高出现的位置与最大波幅一致,即(H1ct)x=x0=Hm。图9展示了量纲一化后的第一波高沿程的变化情况,同时Heller等[25,28]关于沿程波高的试验结果亦绘制在该图中。由图9可知,第一波高的沿程变化规律与第一波峰幅值类似,并且其沿程衰减速率较已有结果更为迅速。图10进一步给出了H1ct/Hm随量纲一传播距离((x-x0)/Hm)的变化情况。从图10中可以看到,不同滑坡体兴波条件下第一波高的沿程分布规律均与Ippen等[29]的预测模型吻合良好：Rd=0时,f=1.36(图10中实线,R2=0.95)；Rd=2.89时,f=0.55(图10中虚线,R2=0.99)；Rd≥ 4.97时,f=0.28(图10中点线,R2=0.98)。对试验数据进行分析还可以发现,量纲一化后的第一波高随量纲一传播距离的衰减速率与初生涌浪的最大波高呈正相关关系。

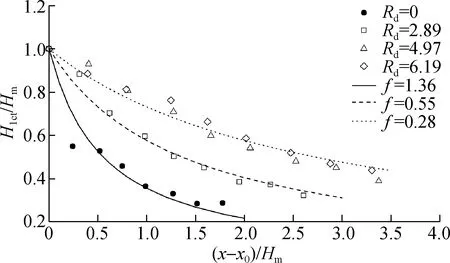
图10 H1ct/Hm随(x-x0)/Hm变化Fig.10 H1ct/Hm as a function of (x-x0)/Hm

3 结 论

本文通过开展三维水池物理模型试验,初步探索滑坡体的散体化对涌浪波动特性的影响作用,取得的主要研究成果如下：

(1) 初生涌浪的最大波幅和最大波高均随滑坡体离散度的增大而减小。

(2) 在滑坡体入水点附近区域,涌浪第一波峰的幅值较第二波峰大；受耗散和色散效应共同作用,涌浪传播过程中第一波峰幅值的衰减速度较第二波峰更快,最终导致第二波峰幅值超过第一波峰幅值。

(3) 涌浪第一波峰幅值和第一波高沿滑动方向的变化规律均符合孤立波波高衰减模型,并且其衰减速度分别与初生涌浪最大波幅和最大波高呈正相关关系；三维条件下第一波峰幅值和第一波高的沿程衰减速度较二维条件下更快,并且先导波波面与孤立波不同。