凹岸崩塌体对急弯河道水力特性的影响

周卓亮,余明辉,李大成,吴 迪,田浩永

(1. 武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072；2. 中国电建集团贵阳勘测设计研究院有限公司,贵州 贵阳 550081；3. 中国电建集团华东勘测设计研究院有限公司,浙江 杭州 311122)

冲积河流在演变过程中常伴随崩岸现象,崩岸不仅会改变河道断面形态,影响近岸水流结构,还会对防洪、航运、供水、水生态等的安全构成威胁。以长江下荆江河段为例,其河岸土体为上部黏土、下部沙土的典型二元结构,抗冲性能差,易发生崩岸[1- 3]。据统计,2003—2018年长江中下游干流河道累计崩岸长度约704 km[4],崩岸的频发严重制约了两岸的经济发展。

二元结构河岸的崩塌过程一般可分为3个阶段[5]:① 下部沙土层的淘刷。当近岸流速超过下部沙土层的起动流速后,沙土层逐渐被水流淘空,上部黏土层部分呈悬空状态。② 上部黏土层的绕轴崩塌。黏土层在重力作用下崩塌,掉落并堆积在近岸坡脚。③ 崩塌后的土体被近岸水流冲散并带走。20世纪70年代中期以来,国内外学者对崩岸机理及发生过程的研究已取得了一定的进展,研究内容多集中于崩岸过程的前2个阶段,但崩岸是一个连续且不断发生的过程,因此对于河岸崩塌发生后的第3阶段,崩塌体对河势调整的研究也不容忽视。Motta等[6]使用RVR弯道水流模型概化了河岸崩塌对弯道水流的影响,认为崩塌体的存在使河道水流高流速区远离河岸；余明辉等[7]通过180°弯道水槽试验认为崩塌体的存在对其附近岸坡崩塌及河床淤积有一定的抑制作用；Hackney等[8]对河岸崩塌处进行实地观测,发现崩塌体在存在的不同时期对河岸侵蚀的影响不同；Deng等[9]提出了一种河床演变及河岸侵蚀的耦合模型,但其一维地形不足以描述弯道近岸复杂的水流条件。以上分析表明,虽然目前对崩岸发生第3阶段中崩塌体堆积于近岸坡脚导致弯道水力特性的改变有了一定的认识,但在以往的研究中,多是从整体上判断崩塌体对河岸侵蚀速率的影响,缺乏对弯道沿程不同区域壁面剪切力的变化研究,也鲜有人关注崩塌体尺寸对弯道水力特性的影响。

弯道水流具有强三维特性,许多学者建立三维水流数学模型研究弯道水流结构。假冬冬等[10]建立窝崩三维数值模型模拟窝塘水流结构及其冲刷过程；Kimiaghalam等[11]运用水动力数值模型,根据河流水位确定河岸上施加的剪应力;Stoesser等[12]分别运用2种CFD模型(RANS模型和LES模型)计算了弯道河流中的湍流流动,结果显示在时均流速的计算上RANS模型比LES模型更加吻合。

本文以荆江石首弯道河段为例,建立三维水流数学模型(RANS模型),对比弯道凹岸崩塌发生前后及崩塌体的尺寸对急弯河段水力特性参数(如水流动力轴线、纵向流速、环流结构和壁面剪切力等)的影响,分析崩塌体存在时弯道不同区域岸坡侵蚀速率的变化趋势。深化对二元结构河岸侵蚀第3阶段的认识,可为河道整治及岸线利用规划提供基础理论及技术支撑。

1 研究方法

以荆江河段石首弯道概化模型[13]为例建立弯道水流三维数学模型。模型弯道段弯曲角度为120°,曲折系数为1.4,在弯顶处河道呈2倍放宽,后逐渐收缩至放宽前宽度。

选用流体体积法(Volume of Fluid)自由液面捕捉技术与雷诺应力模型(RSM)。雷诺应力模型考虑了紊流黏度的各向异性效应,对连续弯道水流运动特性的模拟精度高于标准k-ε模型、RNGk-ε模型及可实现k-ε模型[14]。计算基于明渠模式进行,使用有限体积法离散控制方程；压力速度耦合使用PISO算法；壁面附近流场使用壁面函数法进行求解,所有固体壁面均选择无滑移边界条件；模型水槽入口边界选择质量入口条件,出口边界选择压力出口条件,模型水槽的上表面边界选择压力入口条件。

1.1 控制方程

RSM模型连续性方程和动量守恒方程如下：

(1)

(2)

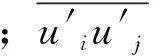
1.2 计算模型网格划分

模型采用结构化六面体网格划分如图1所示。第一层网格到壁面的量纲一距离为y+=Re(u*/U)(Δy/H),其中,Re为雷诺数,u*为近壁面摩阻流速,U为断面平均流速,Δy为网格间距,H为断面水深。壁面处第一层网格需布置在黏性底层和过渡段之外,因此保证3099%,表明计算结果具有足够的精度。

图1 模型计算网格Fig.1 Computational mesh

1.3 模拟工况

三峡水库蓄水后,石首河年均崩岸长度约为2 500 m[5],且崩塌主要发生在弯道凹岸弯顶以下至顶冲点附近处。因此,模拟工况考虑无崩塌体和4种尺寸崩塌体。崩塌体长约3 m,参考谢亚光等[13]试验中的崩塌体横断面形态,分别设置崩塌体横断面形态(宽×高)为工况1(10 cm×10 cm)、工况2(15 cm×10 cm)、工况3(20 cm×10 cm)和工况4(15 cm×5 cm)。崩塌体布置于断面CS9—CS14之间紧邻岸坡坡脚处。模型进口流量Q=50 L/s,出口控制断面水深为0.25 m,保证数学模型与实际河道水流弗劳德数相近。崩塌体位置及断面布置如图2所示。

图2 崩塌体位置及断面布置Fig.2 Location of the slump blocks and cross sections

1.4 模型验证

选取谢亚光等[13]试验中的工况1(进口流量为50 L/s,出口水深为0.25 m)进行模型验证,图3为弯道水槽中沿程断面CS9、CS13量纲一纵向流速的计算值与实测值对比(n为测线编号；U*S=US/U,Z*=Z/H,其中,US为测点流速,Z为测点水深),由图3可知大部分区域计算值与实测值吻合良好,少部分区域由于靠近边壁,水流结构复杂,计算值与实测值稍有差别,但沿垂线变化趋势一致。

图3 量纲一纵向流速计算值及实测值对比 Fig.3 Comparison between modelled and experimental data of normalised longitudinal velocity distribution

2 崩塌体对近岸水流结构的影响研究

2.1 水流动力轴线

弯道水流动力轴线的位置是影响弯道段河岸稳定的重要因素。图4显示了相同流量条件下有无崩塌体时的水流动力轴线。无崩塌体时,水流动力轴线于弯道进口断面CS5的断面中部逐渐往凸岸偏移,至弯顶断面CS9后再逐渐摆向凹岸,直至出口断面CS13后完全贴近于凹岸。相较无崩塌体,崩塌体的存在有将水流动力轴线推向凸岸的趋势,随着崩塌体尺度的增大,推移的幅度越大。比较不同尺寸崩塌体存在时水流动力轴线的位置发现,崩塌体宽度的改变比崩塌体高度的改变对水流动力轴线的影响更大,不同崩塌体宽度条件下的水流动力轴线最大偏移距离为平均河宽的0.014倍,占宽度变幅的40%;而不同崩塌体高度条件下的水流动力轴线最大偏移距离仅为平均河宽的0.004倍,占高度变幅的12%。

图4 不同实验工况下的水流动力轴线Fig.4 Flow dynamic axis under different experimental conditions

2.2 纵向流速及环流发展过程

纵向流速分布和弯道环流结构是弯道水流运动的2个重要物理参数。图5显示了断面CS6—CS14段纵向流速及环流发展过程三维示意图。水流动力轴线变化趋势相似,相较于无崩塌体,崩塌体存在时,断面CS9—CS12最大纵向流速区域远离凹岸,使得近凹岸区域纵向流速减小,近凸岸区域纵向流速增大。断面CS12—CS14,崩塌体的存在使断面面积减小,断面平均纵向流速增大,在水流动力轴线摆向凹岸的共同作用下,近凹岸区域纵向流速增大。值得一提的是,在断面CS9—CS12靠近凸岸边滩区域,纵向流速出现了负值。根据Blanckaert[16]对弯道流动分离阶段的分类,这表明该区域处于流动分离的第2阶段,纵向流速沿横向的分布出现零点,在水流分离区形成竖轴环流。

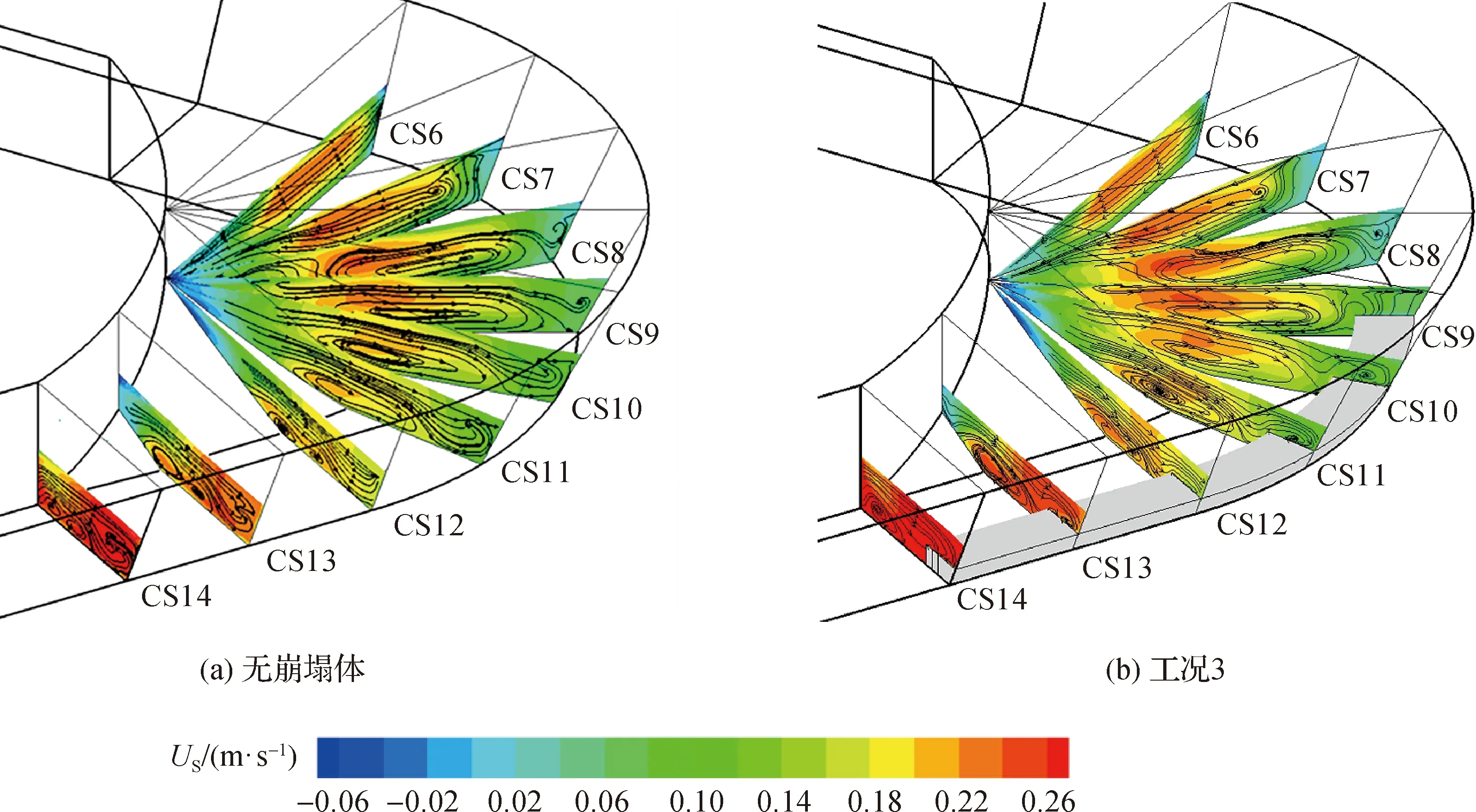
图5 纵向流速等值线及环流发展过程Fig.5 Streamwise velocity contours and circulation development

环流在弯道进口稍下游处(断面CS7)开始形成,顺水流方向在主流区形成一个逆时针环流,称主环流;同时在凹岸靠近水面区域形成了一个较小的顺时针环流,称次环流。主环流沿程发展,在弯顶处(断面CS9)达到最大,几乎占据整个断面;断面CS12后,弯道逐渐束窄,主环流尺寸随弯道束窄而逐渐减小。次环流在断面CS8后形成,其环流强度和尺寸相对主环流都很小,环流方向与主环流方向相反。根据Blanckaert等[17]的研究,这种形成于凹岸的小尺寸环流,不仅受离心力作用的影响,也受湍流动能的影响。这种环流的形成,有利于近岸水流湍流动能的耗散,能有效地降低岸坡侵蚀速率。相较于无崩塌体,崩塌体对弯道主环流的影响较小,仅在断面CS12后,有抑制主环流形成2个环流中心的趋势;但崩塌体的存在使次环流的形态发生了显著改变。

以断面CS13为例,对量纲一纵向流速及断面横向流速矢量展开讨论分析。图6显示了不同尺寸崩塌体对断面CS13的横向流速矢量及量纲一纵向流速的影响,从图6(a)中可以看出,无崩塌体时,主环流存在明显的2个相互重叠的环流中心区域,次环流位于凹岸区域,存在一上一下、一大一小2个方向相反的次环流,位于上方的次环流相较于下方的次环流,环流尺寸和环流强度都更小,其对量纲一纵向流速分布几乎不产生影响。从图6(b)—图6(d)中可以看出,崩塌体的存在对主环流的影响不大,但改变了次环流的方向;相较于无崩塌体,崩塌体存在时次环流位于崩塌体上方,环流方向与原次环流相反,环流尺寸更小。结合量纲一纵向流速等值线来看,无崩塌体时,量纲一纵向流速在次环流的作用下,最大流速区域远离了凹岸；崩塌体存在时,凸岸坡脚量纲一纵向流速增大,量纲一纵向流速超过1.2的水流区域远离凹岸,凹岸附近量纲一纵向流速减小。随着崩塌体尺寸的增加,这种将量纲一纵向大流速区域推离凹岸的现象就越明显,崩塌体高度的增加明显抑制了次环流的发展,而崩塌体宽度的增加则有利于崩塌体上方次环流的发展。

图6 断面CS13横向流速矢量及量纲一纵向流速等值线Fig.6 Cross sectional velocity vectors and streamwise velocity contours in CS13

为分析凹岸次环流强度,引入弯道环流(I)来表示环流的相对强度,I等于横向流速与纵向流速之比,具体计算公式见文献[18]。经计算可知,断面CS13处,崩塌体堆积于凹岸坡脚,主环流强度变化不大,次环流强度比无崩塌体时降低15%左右;同时崩塌体尺寸的改变,对次环流强度的影响不大。

因此可以认为,崩塌体的存在对主环流的影响不大,但改变了次环流的方向;相较于无崩塌体,崩塌体存在时次环流的尺寸和强度更小,但仍能对凹岸岸坡起到一定的保护作用。

2.3 壁面剪切力

根据河岸和河床的形态,将断面分为4个区域：区域1为凹岸坡面未被崩塌体覆盖的区域,区域2为崩塌体堆积于凹岸坡脚的区域,区域3为无崩塌体覆盖的床面区域,区域4为凸岸坡面区域。

壁面剪切力是研究泥沙起动、输移等问题的重要参数[19]。图7显示了无崩塌体和4种不同尺寸崩塌体存在时壁面剪切力的横向分布变化情况。从图7可以看出,在弯道中部(断面CS8)最大壁面剪切力位于凸岸坡面处,出弯后(断面CS12—CS14)最大壁面剪切力逐渐往凹岸偏移,这与主流线的变化规律相似。受主环流的影响,壁面剪切力的横向分布存在2个峰值,其中断面最大壁面剪切力的位置与水流动力轴线所在位置一致,第2峰值一般出现在凸岸坡面上(区域4)。相较于无崩塌体,崩塌体存在时,断面CS8—CS14区域3和区域4内的壁面剪切力均大于无崩塌体时的壁面剪切力,这是由于崩塌体的存在使得最大纵向流速偏向凸岸。比较不同尺寸崩塌体对壁面剪切力的影响,无论崩塌体的宽度还是高度增加,区域3和区域4的壁面剪切力都随之增大。平均壁面剪切力最大增加至无崩塌体时的1.31倍。

图7 无崩塌体及不同工况下壁面剪切力变化情况Fig.7 Variation of bed shear stress in different cases

凹岸坡面处(区域1)的壁面剪切力直接影响弯道凹岸的侵蚀速率。图8显示了无崩塌体和4种不同尺寸崩塌体存在时区域1内壁面剪切力的分布及变化情况。从图8可以看出,崩塌体堆积于凹岸坡脚后,断面CS8处,崩塌体的存在会降低区域1的壁面剪切力；断面CS12处,崩塌体对区域1的壁面剪切力影响不大；断面CS13处,崩塌体的存在会增大区域1的壁面剪切力,仅在崩塌体临坡面处较无崩塌体时有所减小,这与余明辉等[7]在180°弯道水槽中观测到的崩塌体临坡面上下游端附近坡面剪切力较无崩塌体时减小的现象一致。这说明,崩塌体的存在降低了断面CS8—CS12区域1内的壁面剪切力,增加了断面CS12—CS14区域1内的壁面剪切力。随着崩塌体的尺寸的增大,凹岸坡面处的壁面剪切力的变化幅度也越大。

图8 无崩塌体及不同工况下区域1壁面剪切力变化情况Fig.8 Variation of bed shear stress in region 1

图9显示了弯道凹岸(区域1)沿程平均壁面剪切力的变化情况。无论崩塌体是否存在,凹岸坡面平均壁面剪切力在弯顶后沿程的变化趋势都是逐渐增大,直至顶冲点附近达到最大。崩塌体存在时,平均壁面剪切力最大处上移至崩塌体尾部(断面CS14)。相较于无崩塌体,崩塌体的存在对凹岸坡面沿程平均壁面剪切力的影响分为3个部分：① 断面CS8—CS12内凹岸坡面平均壁面剪切力减小,最小减小至无崩塌体时的0.75倍,其中断面CS9为崩塌体的迎水面,水流结构较为复杂,因此平均壁面剪切力的变化趋势略有不同;② 断面CS12—CS14内凹岸坡面平均壁面剪切力迅速增大,并在断面CS14处达到最大,最大增加至无崩塌体时的1.39倍;③ 断面CS14—CS15内凹岸坡面平均壁面剪切力迅速减小后逐渐增大至与无崩塌体时相同。这种变化趋势是因为一方面崩塌体的存在使水流动力轴线远离凹岸,并且减小了凹岸处水流的环流强度,从而使断面CS8—CS12内凹岸坡面平均壁面剪切力减小；另一方面,水流动力轴线经过断面CS12后,逐渐向凹岸偏转,崩塌体的存在减小了凹岸坡面区域的过水面积,使得该区域的纵向流速增大,从而使断面CS12—CS14内凹岸坡面平均壁面剪切力增大。因此可以认为,在断面CS9—CS14区域内,崩塌体堆积于凹岸坡脚,对凹岸坡面平均壁面剪切力的影响为沿程先减小后增大;而在断面CS14之后,由于崩塌体的消失,崩塌体下游凹岸小部分区域内(断面CS14—CS15)流速较缓,凹岸坡面平均壁面剪切力迅速减小。在本试验的条件内,不同尺寸崩塌体对凹岸坡面沿程平均壁面剪切力的影响规律一致,均为先减小后增大。但崩塌体的尺寸越大对断面平均壁面剪切力的影响也越大,其中,断面CS14处不同崩塌体的尺寸对平均壁面剪切力的影响最大,剪切力相对变化幅度达到崩塌体截面积变化幅度的10%;而在断面CS12处不同崩塌体的尺寸对平均壁面剪切力的影响最小,剪切力相对变化幅度仅为崩塌体截面积变化幅度的2%。因此,凹岸沿程平均壁面剪切力相对变化幅度为崩塌体截面积变化幅度的2%～10%。

图9 弯道凹岸沿程平均壁面剪切力变化情况Fig.9 Variation of average bed shear stress in different regions

3 讨 论

以往对于崩岸第三阶段的研究中认为,崩岸发生后,崩塌体堆积于凹岸坡脚,减小水流对河岸的基础侵蚀。Kean等[20]认为崩塌体将纵向大流速区域推离了凹岸,从而减小河岸上的壁面剪切力；谢亚光等[13]通过分析弯道不同部位的崩塌体对弯道水流结构的影响,提出了不同的观点,认为顶冲点上游的崩塌体会减小水流对河岸基础的侵蚀能力,顶冲点下游的崩塌体会增大水流对河岸基础的侵蚀能力。但仅讨论了崩塌体对弯道凹岸整体侵蚀速率的影响,无法反映崩塌体对弯道凹岸沿程不同位置侵蚀速率的影响。

从本文的结果来看,崩岸发生后,崩塌体堆积于凹岸坡脚,不仅对弯道同一断面不同区域内侵蚀速率的影响不同,对弯道凹岸沿程不同位置侵蚀速率的影响也不同。事实上,崩塌体对急弯河道侵蚀速率的影响可分为2个区域：一是河床及凸岸坡面区域(区域3和区域4),崩塌体的存在增大了该区域内的平均壁面剪切力,从而增大了水流对河岸的侵蚀速率；二是凹岸坡面区域(区域1),崩塌体的存在使该区域平均壁面剪切力在崩塌体头部及其上游部分(断面CS8—CS12)减小,在崩塌体尾部(断面CS12—CS14)增大。另外,由于崩塌体的存在,凹岸坡面区域平均壁面剪切力最大的位置也由顶冲点附近移至崩塌体末尾处。因此,崩塌体的存在,降低了水流对其头部及上游区域河岸的侵蚀速率,同时加剧了水流对其尾部区域河岸的侵蚀速率。针对二元结构河岸崩岸第3阶段中崩塌体对河岸二次侵蚀的影响,本文认为,崩塌体堆积于近岸坡脚仅能对其头部及上游区域的近岸起保护作用,而对其尾部区域、河床及凸岸区域,崩塌体的存在均会加剧河岸的冲刷侵蚀。

本文基于弯道三维数值模拟的计算结果初步分析了不同崩塌体尺寸对弯道水力特性的影响,其影响规律适用于石首弯道,是否适用于其他形态的天然弯道还有待研究验证。另外,由于弯道水流的复杂性,不同的来流条件(流量、水位)及相对河岸高度等因素都会影响弯道水力特性。因此,需要进一步的研究来说明不同影响因素间的相互作用关系及其量化方法。

4 结 论

针对二元结构河岸崩塌后崩塌体堆积在凹岸坡脚,以荆江石首河段120°弯道概化模型为例,分析了不同尺寸崩塌体对水流动力轴线、纵向流速、环流结构及壁面剪切力的影响。

(1) 崩塌体的存在使水流动力轴线及纵向流速最大区域远离凹岸。

(2) 崩塌体的存在改变了弯道凹岸处次环流的方向,环流强度比无崩塌体时最大降低15%,不同尺寸崩塌体对环流结构的影响相似。

(3) 崩塌体的存在增大了弯道床面及凸岸坡面区域内的平均壁面剪切力,最大增加至无崩塌体时的1.31倍。崩塌体对弯道凹岸坡面沿程平均壁面剪切力的影响不同,在崩塌体头部及其上游,凹岸坡面的平均壁面剪切力减小,最小减小至无崩塌体时的0.75倍；在崩塌体尾部,凹岸坡面的平均壁面剪切力增大,最大增加至无崩塌体时的1.39倍。崩塌体尺寸的增大,会加剧壁面剪切力的变化幅度,剪切力相对变化幅度为崩塌体截面积变化幅度的2%～10%。