基于能量平衡原理的潜在蒸散发模型构建
鞠 琴,高慧滨,王国庆,郝 洁,王振龙,堵同柱,郝振纯
(1. 河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098;2. 南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏 南京 210029;3. 安徽省·水利部淮河水利委员会水利科学研究院,安徽 蚌埠 233000)
过去1个世纪以来,全球气候变暖已成为不争的事实,是全球普遍关注和重视的热点问题[1- 3]。联合国政府间气候变化专门委员会(IPCC)第六次评估报告指出,自1850—1900年以来,全球地表平均温度已上升约1 ℃,从未来20 a的平均温度变化来看,全球升温预计将达到或超过1.5 ℃[4]。过去的30 a气温均创历年新高,是北半球历史上最热的一段时间[5- 7],相比于IPCC前几期评估结果,气候变化比预想的更加严重[8]。气温的剧烈变化会显著影响流域水文循环的蒸散发环节。流域的实际蒸散发是一个复杂过程,与所在区域的气候、土壤和植被等要素紧密相关,由于实际蒸散发观测资料的缺乏,通常会根据潜在蒸散发来估算实际蒸散发。
潜在蒸散发(ET)是理想条件下下垫面可能达到的最大蒸散发量。目前潜在蒸散发的估算方法主要包括温度法[9]、综合法、辐射法[10]、水量平衡法和质量传导法[11]5类,但这些估算方法在不同地区存在适用性差异[12- 14],在具体应用时,需要首先进行适用性评价,并在必要时进行参数修正[15- 16]。徐俊增等[17]在昆山利用蒸渗仪试验结果评价了11种常用参考作物蒸散发计算方法的适用性,认为FAO56 Penman- Monteith(FAO56 P- M)方法在中国东部湿润地区明显优于其他蒸散发计算方法;阳勇等[18]在黑河上游利用小型蒸渗仪观测结果评价了3种蒸散发估算方法在高海拔山区草地的适用性,发现模拟结果具有明显的季节差异;da Silva Farias等[19]基于线性回归方法对不同的蒸散发估算方法进行校正,发现校正后的计算结果较好;陶新娥等[15]基于线性回归法对所提出误差比例校正法的修正效果进行了评价,结果表明其在闽江流域的潜在蒸散发估算中具有较好的稳定性。然而,目前大部分关于经验估算方法修正的研究仅停留在通过线性回归或逐月误差比例校正来修正经验公式中的参数,对基于试验机理的经验公式修正研究还不够深入,有待进一步探讨。
FAO56 P- M法作为被列入现行《灌溉试验规范:SL13—2015》的潜在蒸散发估算方法,在中国常被用作不同区域蒸散发估算方法适用性的评价标准[20]。基于淮北平原五道沟水文水资源实验站(简称五道沟实验站)的水文气象观测资料,陈言等[21]评估了包括FAO56 P- M、1948 Penman、FAO24 Penman、Priestley- Taylor等在内的7种潜在蒸散发估算方法在该地区的适用性,结果表明这些方法均存在较大误差,其中Penman系列方法的精度最高,但与实测值整体上仍存在10%~15%的低估误差。由此可见,潜在蒸散发的计算方法仍有一定的提升空间。
本文以淮北平原五道沟实验站小型蒸渗仪的潜在蒸散发试验为基础,基于能量平衡原理和波文比,构建了一种新的潜在蒸散发计算模型,采用3组实测数据进行验证,并与现有方法的计算结果进行对比,以期为该地区潜在蒸散发计算提供新思路。
1 研究区概况及试验设计方案
1.1 研究区概况
五道沟实验站(117°21′E,33°09′N)位于安徽省蚌埠市新马桥镇原种场内(图1),是一所平原区大型综合实验站。站点所在地区位于淮河流域南北气候分界线附近,属北亚热带和暖温带半湿润季风气候,四季分明;气温年际变化小,多年平均气温为14.6 ℃,1月平均气温最低,7月最高;太阳辐射充足,多年平均日照时数约2 100 h,多年平均无霜期为212 d,多年平均蒸发量为1 181.3 mm;因常处在冷暖气团交锋过渡带,降水量年际差别大,多年平均降水量为899.0 mm,最大年降水量可达1 212.2 mm,但年内分布相对集中,汛期通常为6—9月,其降水量可占全年2/3。

图1 五道沟水文水资源实验站位置Fig.1 Location of the Wudaogou hydrological experimental station
1.2 试验设计方案
为了研究土壤含水量和气象要素对土壤蒸发及草地蒸散发能力的影响,本文采用五道沟实验站气象场内的小型称重式蒸渗仪群进行蒸散发能力试验,气象场同期观测要素还包括气温、相对湿度、E601水面蒸发、风速、地温和水温等。PVC材质的圆柱筒形小型蒸渗仪内径20 cm,深50 cm,底部密封,以取自大田的原状土填充。
试验方案如表1所示,蒸渗仪布设如图2所示。蒸渗仪按照1—6号依次编号,分成3组进行平行试验,取每组2个蒸渗仪的观测平均值为该组条件下的蒸散发能力。根据是否有覆被,蒸渗仪分为裸土和覆被草皮(狗牙根,低矮植被)2类,分别用于观测裸土表面和草地覆被条件下的蒸散发能力。覆被草皮的蒸渗仪有固定质量和固定水位2种加水方式,其中,1号和4号蒸渗仪每次加水至固定质量,此时土壤体积含水率约为50%,王振龙等[22]指出五道沟实验站的田间持水量为28%~30%,满足本次试验所需要的按蒸散发能力蒸发的饱和状态;2号和5号蒸渗仪每次加水至固定水位,水面高于土壤表面5 mm。
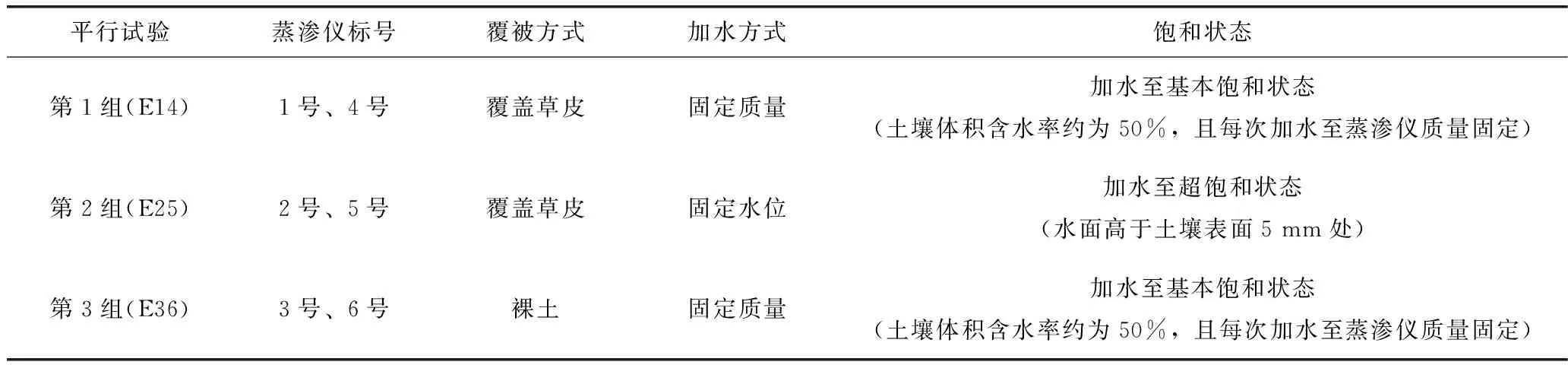
表1 土壤蒸发和草地蒸散发能力试验方案
试验过程中,每天8:00向蒸渗仪加水至饱和,以保证充分供水状态。蒸渗仪观测时间为每天8:00和20:00,观测电子称的精度为1.0 g,约等于小型蒸渗仪中0.053 71 mm的蒸散发。蒸渗仪上覆滑动顶棚,用于雨天时遮挡,减少降水对蒸散发测量的影响以保证观测结果准确性,但出现暴雨天气时,强降水会引起土柱淹没,测量结果受降水影响出现异常值,因此,实际计算时需要剔除异常测量值。本次试验观测时间为2014年8月1日至2015年8月31日,标准气象场的气象要素观测与蒸渗仪观测同步进行。

图2 小型蒸渗仪的布设Fig.2 Installation and arrangement of small lysimeters
2 基于能量平衡的潜在蒸散发模型构建
基于五道沟实验站2014年8月1日至2015年8月31日的水文气象观测资料,本文建立了考虑能量平衡的潜在蒸散发计算模型(LY- ET模型)。
2.1 潜热通量计算公式的推导
忽略极少部分进入植物用于光合作用的能量消耗,地表能量平衡可以写为
Rn=λET+H+G
(1)
式中:Rn为到达地表的净辐射,MJ/(m2·d);λET为潜热通量,MJ/(m2·d);H为显热通量,MJ/(m2·d);G为地表热通量,G≈0.1Rn,MJ/(m2·d)。
λET和H可由下式计算:
(2)
(3)
式中:ρ为空气密度,kg/m3;CP为空气定压比热容,J/(kg·K);γ为湿度计常数,与气压有关,标准大气压下为0.066 4 KPa/℃;e0和e2分别为蒸发面和2 m高度处的水汽压,kPa;T0和T2分别为蒸发面和2 m高度处的气温,K;ra为空气动力学阻抗。
由于实践中ra的直接计算和测量有很大局限性,因而潜热通量和显热通量也很难通过式(2)和式(3)计算,一般可通过涡度相关技术直接获取,两者之比称为波文比(B):
(4)
因此,结合式(1)的能量平衡原理和式(4)的波文比概念得到潜热通量的计算方法为
(5)
2.2 对潜热通量计算公式的修正
2.2.1 平流运动动力项
潜热计算公式(式(5))虽然基于能量平衡理论,但是没有考虑土壤表面水平方向的能量交换,需要引入一个平流运动的动力项(Ea)。与Dalton公式[23]的原理类似,Ea主要考虑风速、水汽压差和温度对蒸散发的影响,计算方式如下:
(6)
f(u)=X1(1+X2u2)
(7)
式中:T″0和Ta分别为土壤表面温度和气温, ℃;es为地表温度对应的饱和水汽压,kPa;ea为气温对应的实际水汽压,kPa;u2为2 m处风速,m/s;X1和X2为拟合系数。
2.2.2 地表净辐射修正系数
式(5)中的Rn一般可由Penman系列公式计算:
Rn=Rns-Rnl
(8)
式中:Rns为短波净辐射,MJ/(m2·d);Rnl为长波净辐射,MJ/(m2·d),详细计算公式见文献[24- 25]。
五道沟实验站布设有涡度塔梯度观测系统,该系统可以直接观测地表净辐射。为进一步验证通过Penman公式计算地表净辐射的可靠性,本文将涡度塔同期观测数据(2014年8月1日至2015年8月31日)与Penman公式计算值进行比较分析,结果如图3所示。从图3(a)可以看出,Penman公式的计算值与涡度塔观测值线性关系较好,相关系数(R)达0.93;Rn的Penman公式计算值(平均值为7.54)整体大于涡度塔观测值(平均值为6.74),但计算值的变幅(变差系数Cv=0.52)小于观测值(Cv=0.71)。由此可以看出,如果直接采用传统的Penman公式对Rn进行计算,会导致潜在蒸散发的计算结果偏大,这在一定程度上也说明了本文提出地表净辐射修正系数(C)的必要性。
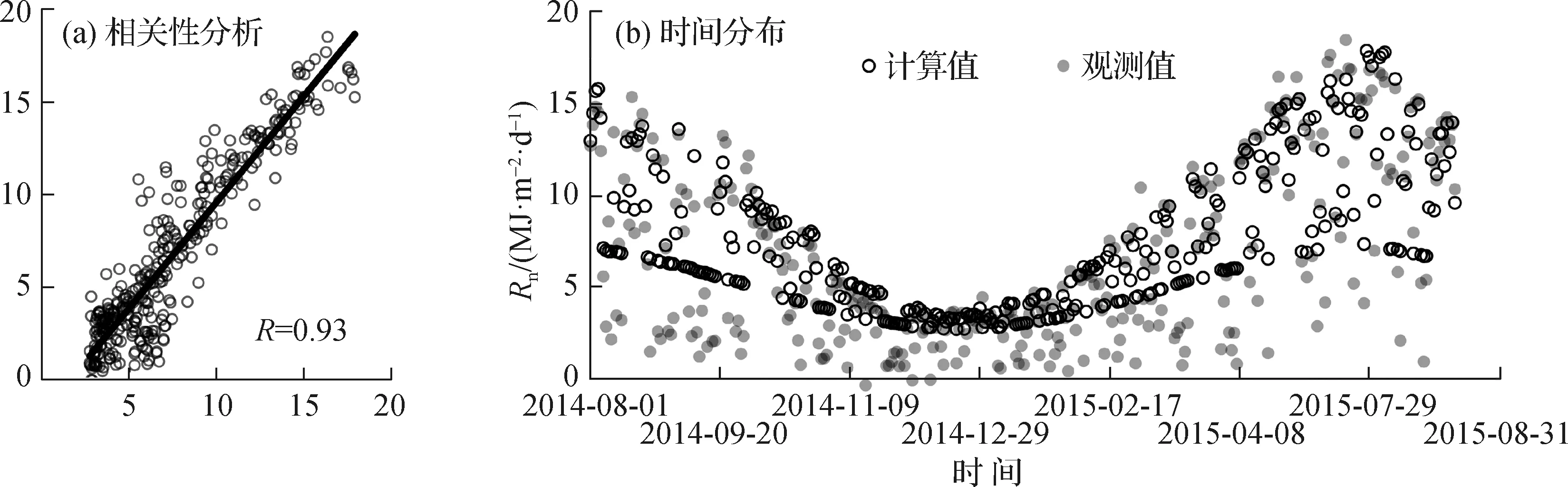
图3 地表净辐射观测值与计算值比较Fig.3 Comparison of observed Rn and simulated Rn
考虑到Penman公式得到的Rn计算值相较涡度塔观测值偏大,因此修正系数可能与地表净辐射负相关的气象要素有关。综合考虑相对湿度、水汽压差和温度等气象要素与Rn的相关性后,发现Rn与相对湿度正相关,但相关系数仅为0.13,故不考虑相对湿度这个因子。而Rn与水汽压差和温度的相关系数分别达0.81和0.80,相关性都较好。因此,本文采用波文比中温度差与水汽压差比值的形式来反映温度和水汽压差对Rn的综合影响。通过计算,Rn与B的负相关系数达0.79,存在显著的负相关关系,修正系数可由下式计算:
(9)
式中:X3为拟合系数。
2.3 LY- ET模型
对潜热通量计算公式(式(5))引入平流运动动力项(式(6)、式(7))和净地表辐射修正系数(式(9))后,最终得到LY- ET模型为
(10)
2.4 精度评价指标
模型的适用性主要通过纳什效率系数(ENS)和均方根误差(ERMS)进行评价。以ENS为主要依据,ENS越接近1,表示模型拟合效果越好,若ENS远远小于0,则表示估算方法不可信;当不同方法的ENS接近时,再通过ERMS综合判断,ERMS越小,则模型拟合效果越好。变差系数是衡量数据离散程度的指标,可用于比较不同单位的数据差异,Cv越大代表数据离散程度越大。各指标计算方法如下:
(11)
(12)
(13)

3 结果与讨论
3.1 土壤蒸散发能力试验数据分析
基于小型蒸渗仪的蒸散发试验数据时间序列为2014年8月1日至2015年8月31日,气象场的观测与蒸渗仪观测同步进行。依据蒸渗仪实测数据测算蒸散发量采用水量平衡原理,方法如下:
(14)
式中:ET为潜在蒸散发,mm;M1和M2分别为第1天和第2天蒸渗仪及其内水土的总质量,g;S为蒸渗仪底面积,cm2。
实测蒸散发和水面蒸发(E601组)对比如图4所示。从整体序列来看,2组草地覆被的蒸散发试验中,固定质量的E14组与固定水位的E25组变化趋势基本一致,相关性最好,R达到0.95;裸土蒸发的E36组与2组有草地覆被的E14和E25组的相关性相对较弱,R分别为0.83和0.89;而E601组和3组蒸渗仪实测结果的相关性都不是很好,R的范围为0.73~0.79,与E36组相关系数最高,E25组次之,E14组最差。从相关性的季节分布上来看(图5),3组蒸散发实测数据整体在夏、秋季线性关系最好,冬、春季较差。

图4 蒸渗仪潜在蒸散发试验观测值和水面蒸发观测值对比Fig.4 Comparison of observed ET of different groups and pan evaporation
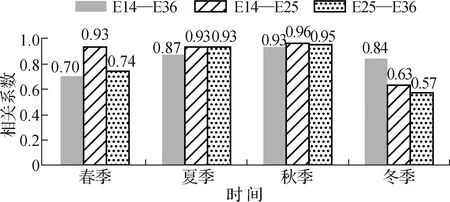
图5 不同试验组观测结果的相关关系Fig.5 Correlation between observation results of different groups
3.2 模型率定及验证
3.2.1 参数率定结果
为了综合考虑潜在蒸散发的年内变化,将每个季节内的实测数据均分为2段,以每个季节的前半段实测数据为率定期,后半段实测数据为验证期。例如,春季(3—5月)选取3月1日至4月15日为模型率定期,4月16日至5月31日为模型验证期,其他季节以此类推。以实测值与模拟值均方差最小为目标函数,首先对拟合参数X1、X2、X3赋初值,然后进行最优化求解。以3组蒸渗仪实测蒸散发数据率定参数X1和X2,以同期涡度塔实测数据率定X3,综合率定结果后的最终参数方案为:X1=0.77,X2=0.54,X3=0.49。
LY- ET模型率定期的模拟结果如图6所示,有草地覆被的E14(R=0.92)和E25(R=0.93)2组的实测值与模拟值相关关系较好,而裸土表面的E36组实测值与模拟值相关性较低(R=0.86)。由此可以看出,基于能量平衡的土壤潜在蒸散发模型在一定程度上更适用于有草地覆被情况下的蒸散发模拟。
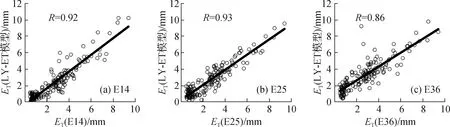
图6 率定期潜在蒸散发实测值与模拟值比较Fig.6 Comparison of observed ET and simulated ET during calibration period
3.2.2 潜在蒸散发模拟效果的验证及季节分布
根据上述参数率定结果计算验证期的ET,从实测值与模拟值的线性关系(图7)来看,验证期的实测值与模拟值仍然具有很好的相关关系,有草地覆被的E14和E25 2组相关系数高于裸土表面的E36组。其中,固定水位加水方式的E25组整体表现(R=0.93)仍优于固定质量的E14组(R=0.88),并且验证期内2组拟合精度之间的差异比率定期更明显,表明植被生长引起的误差在一定程度上不可忽略,在条件满足的情况下,有覆被的蒸散发测量应尽可能避免使用固定质量方式,减小观测误差。

图7 验证期潜在蒸散发实测值与模拟值比较Fig.7 Comparison of observed ET and simulated ET during verification period
从实测值与模拟值的季节分布(图8)来看,相对于裸地表面的E36组,有草地覆被的E14和E25 2组模拟值与实测值的整体变化趋势在4个季节更加一致。但是春、夏季辐射大,气温高,ET整体较大,波动也更剧烈(LY- ET模型春、夏季Cv=0.53);秋、冬季ET偏小且更为集中(LY- ET模型秋、冬季Cv=0.34);与模拟值相比,实测值整体变幅更大。
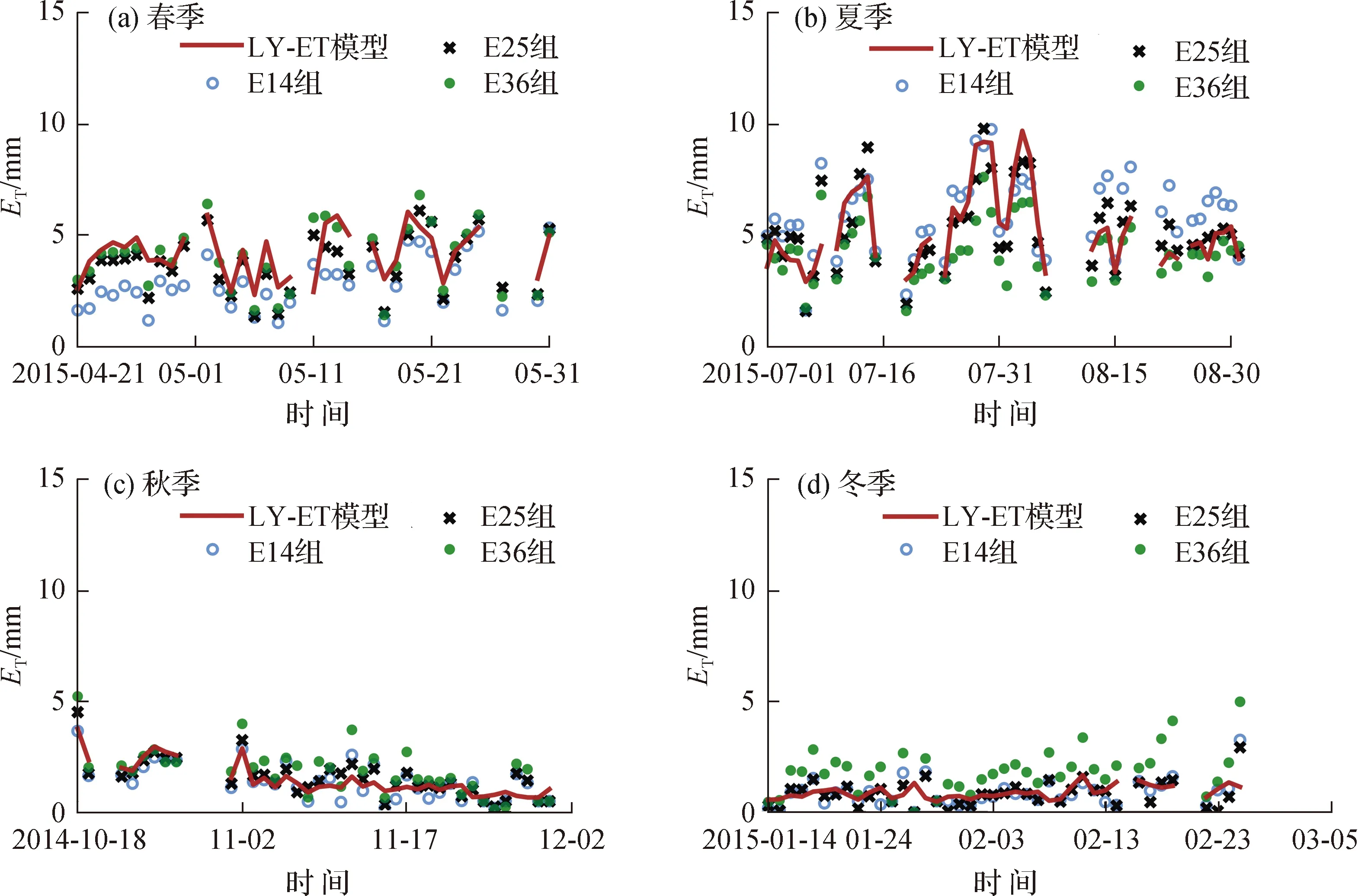
图8 验证期潜在蒸散发实测值与模拟值的四季分布Fig.8 Seasonal distribution of observed ET and simulated ET during verification period
3.3 模型评价
现有的众多潜在蒸散发估算方法各有其适用性和局限性,为了进一步评估LY- ET模型的可靠性,本文选取1948 Penman、FAO24 Penman、FAO56 P- M、Priestley- Taylor、Hargreaves- Samani和Irmark- Allen共6种常用计算方法[26- 27]的模拟结果作为对比,进一步评价LY- ET模型效果。
表2给出了各潜在蒸散发估算方法在验证期的模拟结果精度,其中,在有草地覆被的2组(E14和E25)中,LY- ET模型结果的ENS最接近1,同时ERMS最小,精度指标均为最佳,随后是Priestley- Taylor公式、Penman系列公式和其他经验公式;但LY- ET模型对裸土表面的E36组的模拟效果不佳,ENS仅为0.46,与Penman系列公式精度存在较大差距。

表2 不同方法精度评价指标统计
对整体模拟结果更优的E25组进一步绘制泰勒图(图9),通过σ、R和ERMS的综合表现可以更直观地看出,LY- ET模型的计算结果最接近E25组实测数据所代表的参考点,整体表现最优,表明LY- ET模型在该地区草地覆被条件下的潜在蒸散发估算中具有很强的适用性。

图9 基于E25组验证期实测结果的不同计算方法精度比较Fig.9 Performance comparison of different methods based on observed data from group E25 during verification period
目前已有的众多潜在蒸散发估算模型及相应改进形式基本都只能在特定气候条件下保证有效精度,例如得到广泛认可和应用的Penman系列公式,常被作为无资料地区其他计算方法的评价标准[28],但其对输入资料要求高,且计算参数时会引入较大误差[29],在湿润地区也会出现较大偏差[30];而以Hargreaves为代表的基于温度的估算方法在时间尺度较小时存在较大误差[31]。因此,应用研究区域实测资料对计算方法进行评估和修正能够有效保证选用方法的适用性,进而得到该地区实际气象条件下的可靠计算结果。
本文构建的LY- ET模型虽然基于能量平衡理论,但是也充分考虑了水汽压差、风速、地表温度和气温等因素的影响,模型适用范围较广;同时,模型和方法的可靠性经过了不同下垫面蒸渗仪实测数据的验证。需要指出的是,LY- ET模型对有草地覆被的2组(E14和E25)实测蒸散发能力的模拟效果明显优于Penman系列公式和其他经验公式,但对裸土表面的E36组蒸渗仪观测结果的模拟要劣于Penman系列公式结果,下垫面的不同可能是模拟效果出现差异的主要原因,从这个角度来看,本文构建的LY- ET模型对于蒸发面为充分供水(达田间持水量)、有植被、大而均匀的土壤表面的适用性可能更具优势,但目前涉及该方面的研究缺乏长期有效的观测数据支撑,仍需进一步研究证实。
4 结 论
本文从能量平衡原理入手,结合波文比的概念,引入地表净辐射的修正参数,建立了一种新的潜在蒸散发计算模型,基于小型蒸渗仪观测试验的土壤蒸发和草地覆被蒸散发能力实测数据对模型进行了率定与验证,并进一步对比分析了该模型与6种现有常见计算公式的模拟精度,以评价模型的适用性,主要结论如下:
(1) 2组草地覆被的蒸散发试验中,不同加水方式的观测结果变化趋势基本一致,具有较高的相关系数,但都与裸土蒸发组相关性略差一些;E601水面蒸发组与裸土蒸发组实测结果的相关性最高,与有草地覆被组相关性较差;3组蒸散发实测数据均在夏、秋季线性关系最好,冬、春季较差。
(2) 率定期有草地覆被的固定质量组(E14)和固定水位组(E25)模拟值与实测值相关关系非常好,而裸土表面的E36组实测值与模拟值相关性较低。不同加水方式的差异主要体现在验证期,E25组拟合效果优于E14组,说明采用固定水位方式测量可以减少草皮生长导致的潜在蒸散发观测误差。
(3) 与6种现有常见计算公式相比,LY- ET模型的精度指标在有草地覆被的E14组(ENS=0.75,ERMS=1.16)和E25组(ENS=0.86,ERMS=0.87)中均为最佳,整体表现最优;对于裸土表面的E36组(ENS=0.47,ERMS=1.24)模拟效果劣于其他计算方法,表明LY- ET模型更适用于有草地覆被条件下的蒸散发估算,在淮北地区具有一定的适用性与优势。

