带收获率参数的生物模型稳定性分析

傅仙发

（湄洲湾职业技术学院，福建 莆田 351119）

引言

随着社会的不断发展，人类对于生物资源的依赖不断增加，使迅速发展的生物数学面临着一个重要的问题——如何有效地管理和开发现有的生物资源，保持生物资源的多样性和稳定性，使资源能为人类长期使用，得到可持续发展。为此，首先要考虑到生态平衡的稳定性问题。捕食者-食饵模型作为近些年生物数学的主要研究方向[1]，模型的稳定性问题成为众多学者关注的焦点，相关的研究文献也较多，但通过在模型中引入收获率参数来分析生物模型稳定性方面的文献不多。本文则是通过在捕食者群体中引入收获率参数，来分析一类Holling-II型捕食者-食饵模型的稳定型问题，研究收获率参数对于生物模型稳定性的影响，为生态种群的可持续性提供一定的理论支持。

文献[2,3]对于以下Holling-II型捕食者-食饵模型

其中，β,γ,δ都是正常数。对模型（1）引入正的收获率参数h，假设捕食者以连续恒定收获率捕食，可将公式（1）表示为

这就是本文所要研究的捕食者带收获率参数的捕食系统模型[4-5]。

1 系统的平衡点及其稳定性

若仅仅从生物学角度和意义方面来看，生物模型在第一象限内的动力学性质是我们所要关心的，即只关注满足生物意义的初始条件x1(0)≥0，x2(0)≥0。为此，可以绘制出捕食者与食饵在第一象限内的等值线[4-6]，如图1所示：

图1 系统（2）捕食者与食饵在第一象限内的等值线

从图1中可知，收获率参数h对系统（2）平衡点的个数起决定性作用。当h足够大时，系统（2）不存在平衡点，而且种群将会难以维持，逐步走向灭绝。因此控制收获率h的最大承受量，是自然（或可再生）资源的优化管理的需要，也是确保捕食者种群可以继续维持的关键[4]。

还可求得

（i）当h＞h0，δ＞γ时，在第一象限内系统（2）不存在平衡点；

（ii）当h=h0，δ＞γ时，在第一象限系统（2）存在唯一平衡点P0；

（iii）当h＜h0，δ＞γ时，在第一象限内系统（2）存在两个平衡点

在数学上系统（2）的曲面被称为鞍结点曲面[4，5，7]。由定理可知，

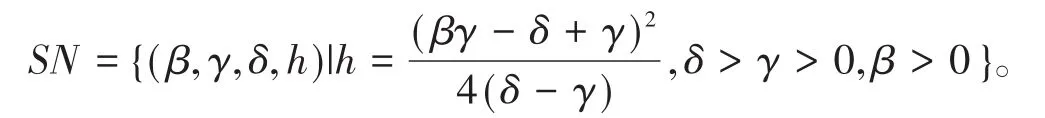
是一个鞍结分岔曲面。并且当正参数β,δ,γ从曲面的一端穿到另一端时，系统（2）经历了一个鞍结分岔，其平衡点的数量从0个变为2个，并且这2个平衡点分别是双曲鞍点和结点。对此鞍结分岔的生物学解释是，当h＞h0时，捕食者趋于灭绝，系统崩溃[4]；当h≤h0时，捕食者不会灭绝[2，8，9]。下面给出了系统（2）在特定值下,收获率参数发生微小变化时的三组鞍结分岔图（见图2（a-c）所示）。

图2 系统（2）的鞍结分岔

2 捕食者带收获率模型的Hopf分岔

为简便起见，本文仅对系统（2）发生Hopf分岔的参数条件进行分析。

若系统（2）在平衡点(x͂1,x͂2)附近产生了Hopf分岔，此时对应系统的雅克比矩阵为[4，5，10]：

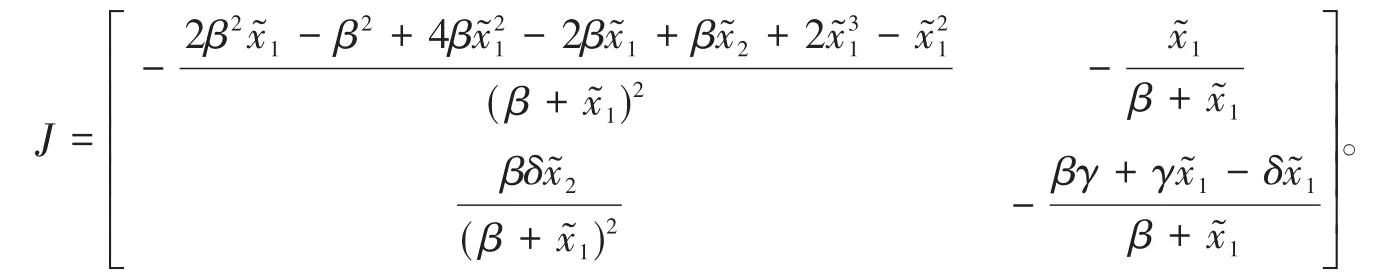
很明显地，当发生Hopf分岔时，矩阵J有一对纯虚特征值，于是得到了系统（2）发生Hopf分岔的参数条件：

参数发生变化时的稳定性变化情况，可见选取合适的参数值产生的Hopf分层图。下面作出了系统（2）在给定特定值下，收获率参数发生微小变化时的Hopf分岔图[6，10（]见图3（a-b）所示）。

图3 系统（2）的Hopf分岔图

3 结语

对一般的Holling-2型捕食者-食饵模型（1），本文将捕食者的收获用收获率参数h来表示，通过对生物系统（2）的平衡点和稳定性分析，给出了在特定值下的鞍结合Hopf分岔图，得出了收获率参数对维护生物种群稳定、防止种群灭绝都具有重要的参考价值。