基于改进型PEM和L指标的含风电场电力系统静态电压稳定评估

吴亚宁，罗毅，雷成，黄豫，梁宇，周生存，聂金峰

(1. 强电磁工程与新技术国家重点实验室(华中科技大学 电气与电子工程学院)，湖北 武汉 430074；2. 南方电网能源发展研究院有限责任公司，广东 广州 510530)

0 引言

为加速推进实现碳达峰、碳中和的战略目标，大力发展新能源是必由之路。风电作为新能源发电的主力军发展迅速，截至2021年底[1]，中国风电新增装机容量48 GW，累计装机已达328 GW，约占总装机容量的13.8%，风电已逐渐成为推动中国能源转型、促进可持续发展的重要力量[2]。但是，风电的随机性和间歇性给电力系统安全稳定带来严峻挑战，电压稳定问题日益凸显，近年来，国内外已发生多起因电压崩溃引发的大面积停电事故[3]。因此，深入开展含风电场电力系统电压稳定性方面的研究对于保证电网安全稳定运行具有重要意义。

电压稳定问题作为电力系统稳定性研究的重要组成部分一直备受关注。目前关于电压稳定的研究在理论上已取得一定的进展，并形成了较为完善的评估指标体系，主要有电压灵敏度指标、潮流雅克比矩阵指标、崩溃点指标、负荷裕度、局部电压稳定指标(L指标)等[4-8]。其中L指标凭借物理意义清晰、计算速度快、不涉及崩溃点处雅克比矩阵病态化难于求逆等优点，在电压稳定分析中获得了广泛应用。文献[9]利用L指标识别系统电压稳定薄弱节点进而完成在线电压稳定局部的监控；文献[10-11]分别将L指标与动态经济压差法和复杂网络理论相结合以识别系统的电压薄弱节点，指导系统无功分区优化调节；文献[12]基于L指标推导了负荷节点电压稳定裕度；文献[13]给出了简化L指标的全微分方程，从而分析系统参数变化对电压稳定的影响。

风电大规模并网后使得系统电压稳定评估过程中的不确定性增加，须研究相应的概率化分析方法[14]。文献[15-16]采用Monte Carlo法模拟抽样，虽然能较为真实地反映系统状态，但反复抽样计算消耗的大量时间成本限制了其应用范围；文献[17]详细推导了L指标对节点注入功率的灵敏度，进而利用解析法完成快速评估，但是当风电功率波动较大时，线性化灵敏度矩阵产生的误差不容小觑；文献[18]基于可信性模糊理论模拟风速变化，提出了可信性意义下的静态电压稳定指标，但是其隶属度函数的选取较为繁琐，实用性仍有待验证；文献[19]利用随机响应面法将风电概率问题转化为确定性的非线性规划问题来实现电压稳定的概率评估，但涉及复杂的数学推导和计算，实际运用效果欠佳。相比于上述方法，点估计法(point estimate method，PEM)则是处理不确定因素的有效工具[20-21]，通过少量的计算成本便可获得较高的计算精度，因而被广泛用于含不确定性的电力系统分析计算中[22-28]。现有PEM中应用最多的是两点估计和三点估计法，其中后者更具优势，但是在处理含风速等典型非正态分布的多随机变量时存在一定偏差，将其用于含风电场电力系统电压稳定分析时，如何减小评估误差是个迫切需要解决的问题。另外，风电并网给电力系统静态电压稳定带来的影响具有不确定性，如何实现其量化分析对于指导电力系统规划运行具有重要意义，目前尚缺乏相关的评价指标，因而难以实现并网风电场对电力系统静态电压稳定影响的量化评估。

综上，本文提出一种基于改进型PEM和局部电压稳定L指标的含风电场电力系统静态电压稳定评估方法。首先，基于传统2n+1法提出一种改进型PEM来计算L指标各阶矩和半不变量，并结合Cornish-Fisher级数展开获得其概率分布；然后，结合效用函数理论定义并计算各节点电压失稳风险度从而完成系统静态电压稳定评估；最后，引入风电并网电压稳定因子分析风电并网对系统静态电压稳定的影响。通过算例验证本文所提方法的有效性。

1 处理不确定性因素的PEM

1.1 点估计理论

理论上取的点位置越多，点估计的精度越高，但随着m的增大，变量和方程的数量增加需引入泰勒级数中更高阶项，此时会引入多元函数泰勒级数高阶项中的交叉项和变量的更高阶中心矩，使方程类型更为复杂，可能会使得位置与权重系数出现无意义的非实数解，同时计算效率也会降低，因此m一般不超过3。

1.2 基于2n+1方案的改进型PEM

1.2.1 传统PEM

当m=2时称为两点估计法即2n方案，各估计点的位置和权重系数[23]为

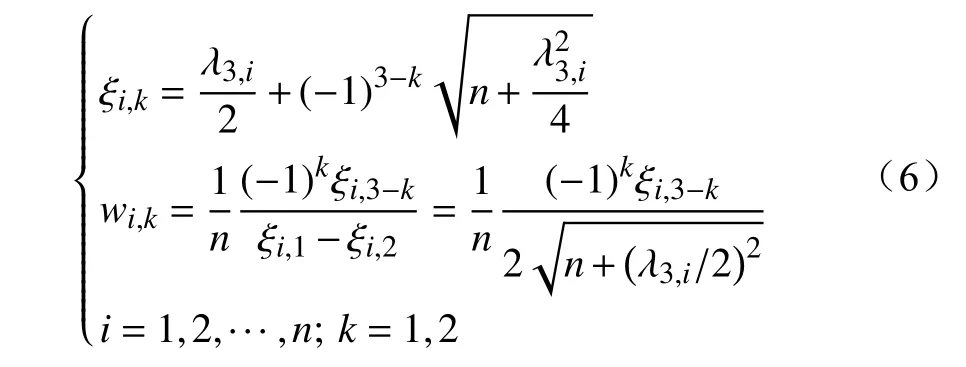
2n方案仅在每个随机变量处取2点计算效率较高，但随着变量维数n的增加，由式（6）可知估计点位置可能会偏离定义域。

当m=3时称为三点估计法，即在每个变量处取3个估计点，但若控制每个变量均在其均值处取点，则存在n个位置相同的估计点，故又称2n+1方案，相应的各估计点的位置和权重系数[23]为

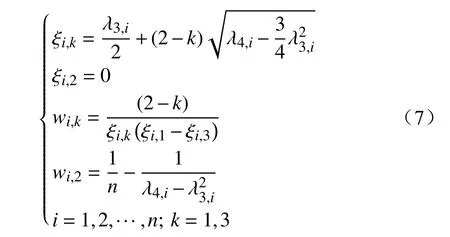
由式（7）可知，相比于两点估计，2n+1方案的位置系数不受变量规模影响，且同时用到了随机变量的偏度和峰度信息，而仅须增加一次计算量，因此相比2n方案具有更高的精度和计算效率。

1.2.2 改进型PEM

2n+1方案中位置系数用到了变量峰度信息，峰度越大说明变量存在极端值，相应的位置系数绝对值增大以考虑变量分布的尾部效应。但是在处理多随机变量时，当n≥3后均值处点的权重会显著减小，甚至出现负值，与其物理意义不符，这可能会降低点估计的精度。因此，当n≥3时可在原有的2n+1方案的基础上增加一组均值附近估计点，相应的位置系数和权重为

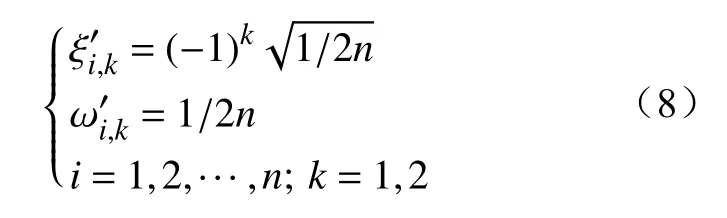
结合式（7）（8）计算待求变量Y的各阶原点矩的统计信息为

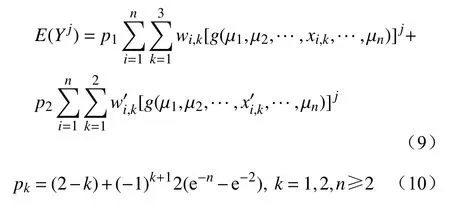
式中：p1、p2为待求变量各阶原点矩的结果权重系数。

由式（8）（9）可知，改进型PEM在处理多变量时，增加的估计点位置不仅靠近均值处，且所得结果占有一定的权重，从而有效提取了变量均值附近处的信息，弥补了2n+1法在处理多随机变量时存在均值处权重负效应的缺陷。特别地当n=2时，p1=1，p2=0，此时改进型PEM即为2n+1方案，这是考虑到2n+1法在处理双随机变量时一般不存在均值处权重为负的情形，已具有较高精度。此外，由式（10）可知，p1和p2分别具有一定的下限和上限，这是为了保留2n+1法具有可根据变量峰度来有效提取变量尾部信息的优点，避免均值附近信息的过度弥补导致尾部信息丢失。

究其本质，所提的改进型PEM试图通过增加估计点的数量来提升估计精度，虽然需额外增加计算量，但由于增加的估计点无须进行位置系数和权重系数的复杂计算，不涉及输入变量的更高阶矩，也不存在估计点位置溢出变量定义域的弊端，因此实际运用起来简便可行。

1.3 半不变量与Cornish-Fisher级数

半不变量[22]作为随机变量的一种数字特征却很难直接计算，需要涉及随机变量的特征函数和矩母函数。而实际运用中若已知随机变量的有限阶原点矩，则可以利用半不变量与原点矩的对应关系计算出随机变量的有限阶半不变量[23]，即

2 局部电压稳定L指标

若系统电压稳定，则对应L＜1；若系统电压失稳，则对应L＞1；L=1对应系统临界稳定。L指标与PV曲线的变化关系趋势[12]如图1所示。

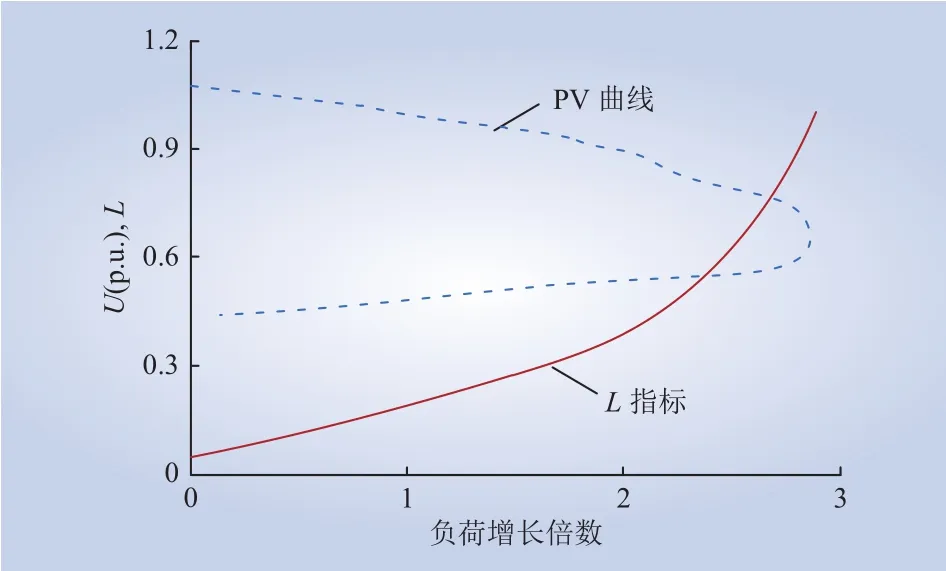
图1 L指标与PV曲线关系变化趋势Fig. 1 Change trend of relationship betweenLindex and PV curve

3 含风电场电力系统静态电压稳定评估

3.1 风电与负荷功率的不确定性模型

3.1.1 风电场出力模型

3.1.2 负荷模型

3.2 风险偏好型评估指标

效用函数理论[29]源于经济学领域，它反映投资者对风险的持有态度，主要分为3类：偏好型、中立型和厌恶型。本文采取风险偏好型，此类函数边际效用递增，从而可定义各节点L指标严重度函数Si(Li)为

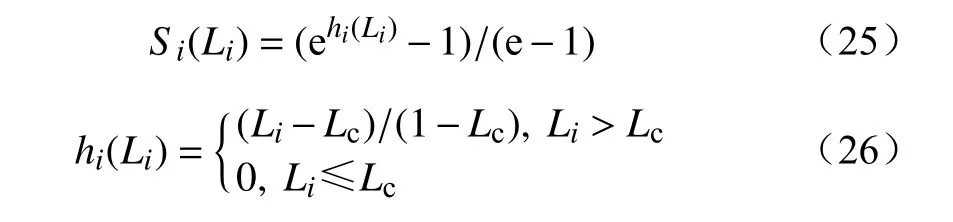
式中：Lc为L指标的警戒值；hi(Li)为i节点L指标越警限量；Li为i节点L指标。

该定义下的严重度函数如图2所示。

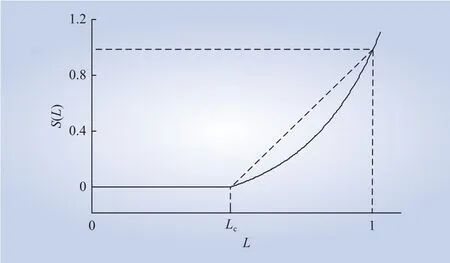
图2 严重度函数S(L)曲线Fig. 2 Severity functionS(L) curve

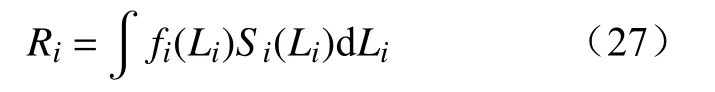
进一步可定义系统静态电压失稳风险度Rs为

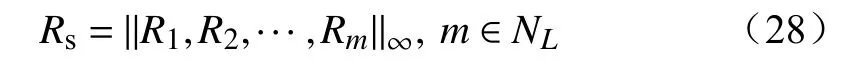
以Ri为指标，可以完成对各节点的静态电压稳定评估，有效辨识系统中存在电压失稳潜在风险的薄弱节点，以便于采取一定的控制措施；以Rs为指标，可以分析风电对系统的静态电压稳定的影响，为电力系统规划运行等提供参考。

3.3 风电并网影响分析指标

为进一步分析风电对系统静态电压稳定的影响，本文基于风电容量可信度[30-31]的计算方法定义风电并网电压稳定因子(简称稳定因子)。风电容量可信度的计算分析过程可理解为：根据所选取的系统某一参考指标，将出力随机波动的风电等效为确定的常规机组来简化风电对系统该指标水平的影响研究。因此从这个思路出发，若选取3.2节中系统静态电压失稳风险度Rs作为参考指标，则可以定义一种风电并网电压稳定因子λ来简化风电场对系统静态电压稳定的影响分析，λ的计算公式为

式中：PWG为风电场装机容量；PG为维持系统相同静态电压失稳风险度水平下的常规机组替换容量，特别地若PG为负值时，则PG等价于负荷。

一般来说，在负荷节点附近增加常规机组(或负荷)对于系统静态电压稳定性是有提升(或降低)作用的，因此λ的大小可直观反映风电对系统静态电压稳定的影响程度。若λ＞0，意味着风电并入后对系统静态电压稳定性有提升效果，反之λ＜0则是降低效果，且绝对值越大效果越明显。

3.4 评估流程

本文提出的基于改进型PEM和L指标的含风电场电力系统静态电压稳定评估方法，将复杂的不确定性问题转化为确定性计算，基本步骤如下。

（1）统计风电场风速历史数据，拟合风速概率分布，结合风机参数确定风电场出力的概率模型，同时确定系统负荷的典型概率模型；

（2）计算风电场出力与系统负荷的均值、标准差、偏度和峰度等统计量，利用改进型PEM由式（7）～（10）确定各估计点的位置和权重大小；

（3）针对每个估计点进行确定性潮流计算，根据式（18）（19）计算获得L指标的各阶矩信息，由式（11）（12）计算L指标的各阶半不变量，并采用Cornish-Fisher级数展开求得各节点L指标的概率密度与分布函数；

（4）结合风险偏好型效用函数由式（25）～（28）计算各节点静态电压失稳风险度，完成含风电场电力系统静态电压稳定的快速评估，有效识别系统中存在的电压薄弱节点；

（5）基于系统静态电压失稳风险度，由式（29）计算风电并网电压稳定因子，进一步分析风电并网对系统静态电压稳定的影响。

4 算例分析

4.1 算例简介

分别以改进的IEEE-14和39节点系统进行算例分析。（1）将IEEE-14节点标准系统中节点6改为PQ节点，同时分别在节点4和6安装额定容量为120 MW和100 MW的风电场，为便于模拟静态电压失稳风险，将其负荷在原有基础上等功率因数增长0.4倍，且服从方差为的正态分布即；（2）在IEEE-39节点标准系统中的节点4和16处分别安装额定容量为600 MW和500 MW的风电场，负荷服从方差为的正态分布。假设上述风电场均配备充足的无功补偿装置使其并网功率因数为1，风速概率模型采用两参数Weibull分布，具体相关参数如表1所示，功率基准值均取为100 MV·A，其余参数不变。

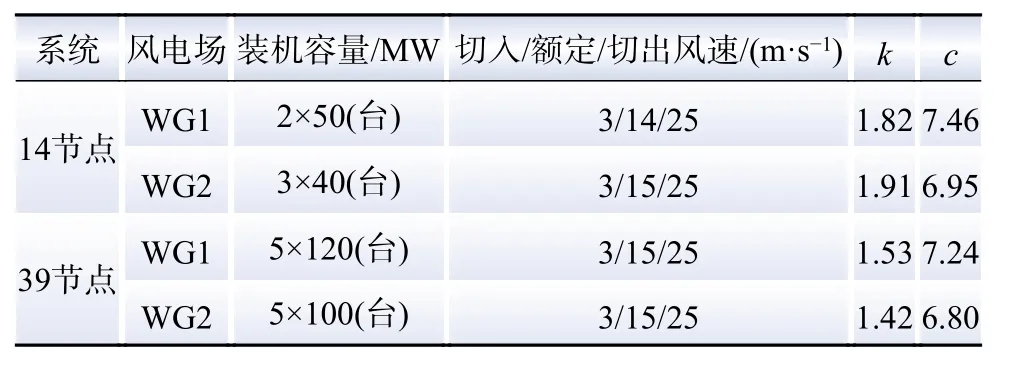
表1 风电场相关参数Table 1 Wind farm related parameters

4.2 L指标的概率分布计算

采用改进型PEM计算节点L指标的概率分布，其中Cornish-Fisher级数取前5项和。图3给出了IEEE-14节点系统中负荷节点的L指标累积分布函数的计算结果。可以看出，与系统平衡/PV节点电气距离较近的节点4和5的L指标水平偏低，静态电压稳定水平较高；而电气距离较远的节点13和14的L指标水平偏高，静态电压稳定水平较低。这与文献[10]的研究结果基本一致，初步说明了所提方法的合理性。

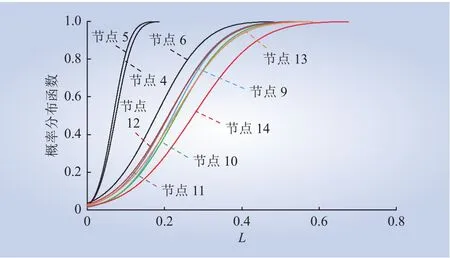
图3 IEEE-14节点系统中L指标概率分布函数Fig. 3 Probability distribution function of Lindex in IEEE-14 node system

为进一步验证所提方法有效性，采用传统2n+1法进行计算，并以Monte Carlo抽样10 000次的计算结果为参考。随机选取14节点系统中的节点10和39节点系统中的节点18为例，其相应的L指标的概率密度和分布函数拟合结果分别如图4和图5所示。

图4 IEEE-14节点系统L指标计算结果Fig. 4 Calculation results of Lindex in IEEE-14 node system

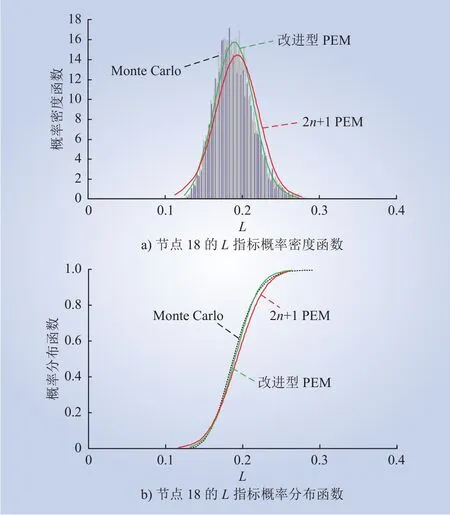
图5 IEEE-39节点系统L指标计算结果Fig. 5 Calculation results ofLindex in IEEE-39 node system

将图4和图5结果与Monte Carlo抽样分布对比，不难发现改进型PEM的拟合效果更令人满意。2n+1法拟合的密度函数集中度较低，改进型PEM通过增加估计点有效提取了均值附近处的信息，所得结果更符合Monte Carlo抽样分布。

为衡量改进型PEM提升L指标估计精度的性能，定义各负荷节点L指标的均值与标准差的相对误差指标 εi,µ和 εi,σ分别为

式中：µi,MCS、µi,PEM分别为Monte-Carlo法 和PEM法计算出的i节点L指标均值；σi,MCS、σi,PEM分别为Monte-Carlo法和PEM法计算出的i节点L指标标准差。

图6给出了不同系统中负荷节点L指标的均值与标准差相对误差，不难看出改进型PEM可以有效降低二者的拟合误差，且对于标准差误差的改善作用更为明显。这与图4和5结果一致，说明改进型PEM主要是提升了变量分布的集中程度，有效弥补了2n+1法在处理含非正态分布的多变量时由于尾部信息的过度提取导致均值附近信息丢失的不足，使得变量分布更接近于实际的Monte Carlo抽样分布，从而验证了所提方法的有效性。

图6 L指标计算的相对误差Fig. 6 Relative error ofLindex calculation

但需要注意的是，所提改进型PEM是在原有2n+1法基础上加以改进的，为了保留2n+1法可根据变量峰度大小有效提取变量尾部信息的固有优点，增加的估计点的结果权重系数不应太大，否则可能会导致图4和5中拟合的密度函数集中度过高从而导致尾部信息缺失，造成拟合精度不升反降的现象。由于本文所提方法设定了结果权重系数的上、下限，因此可以预计当n＞3时改进型PEM将会有类似的提升效果，限于篇幅本文不做详细研究。

4.3 静态电压失稳风险评估

在上述改进的IEEE-14和39节点系统中分别设定L=0.3和0.2为警戒值，当L超过警戒值后，严重度函数随之增大，由此利用3.2节中的电压失稳风险度和4.2节L指标分布结果计算节点静态电压失稳风险度，结果如表2和3所示，按其大小进行排序，其中排序靠前的部分结果如表4所示。

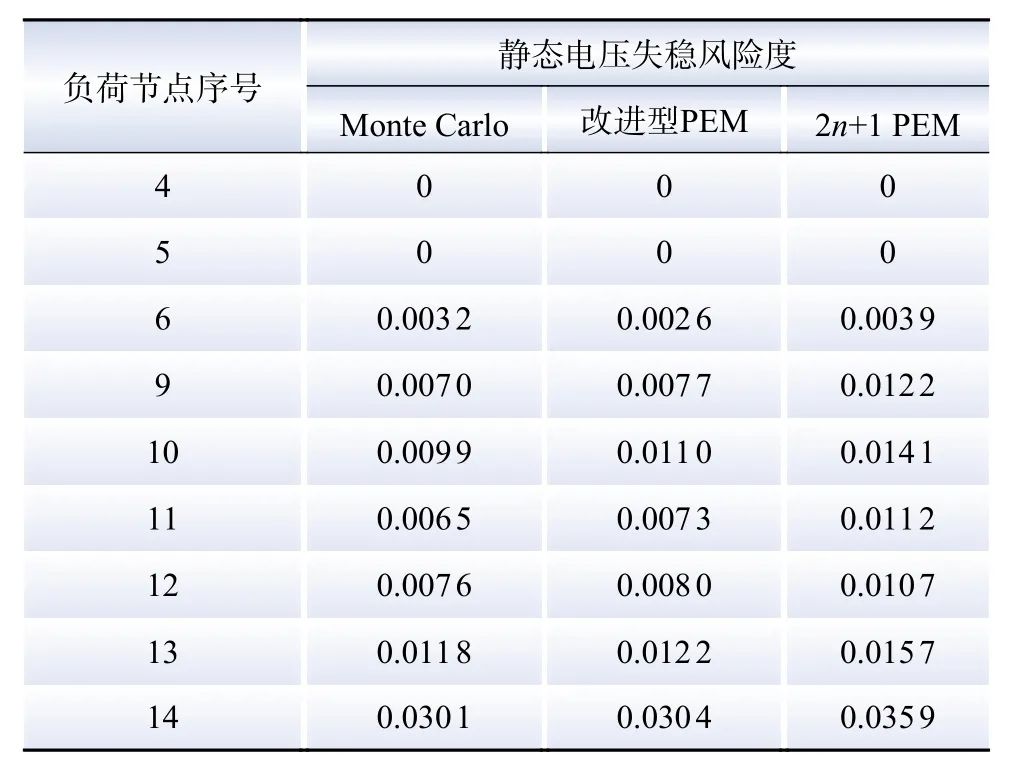
表2 改进IEEE-14节点系统中负荷节点电压失稳风险度Table 2 Risk of voltage instability of each load node in the improved IEEE-14 node system

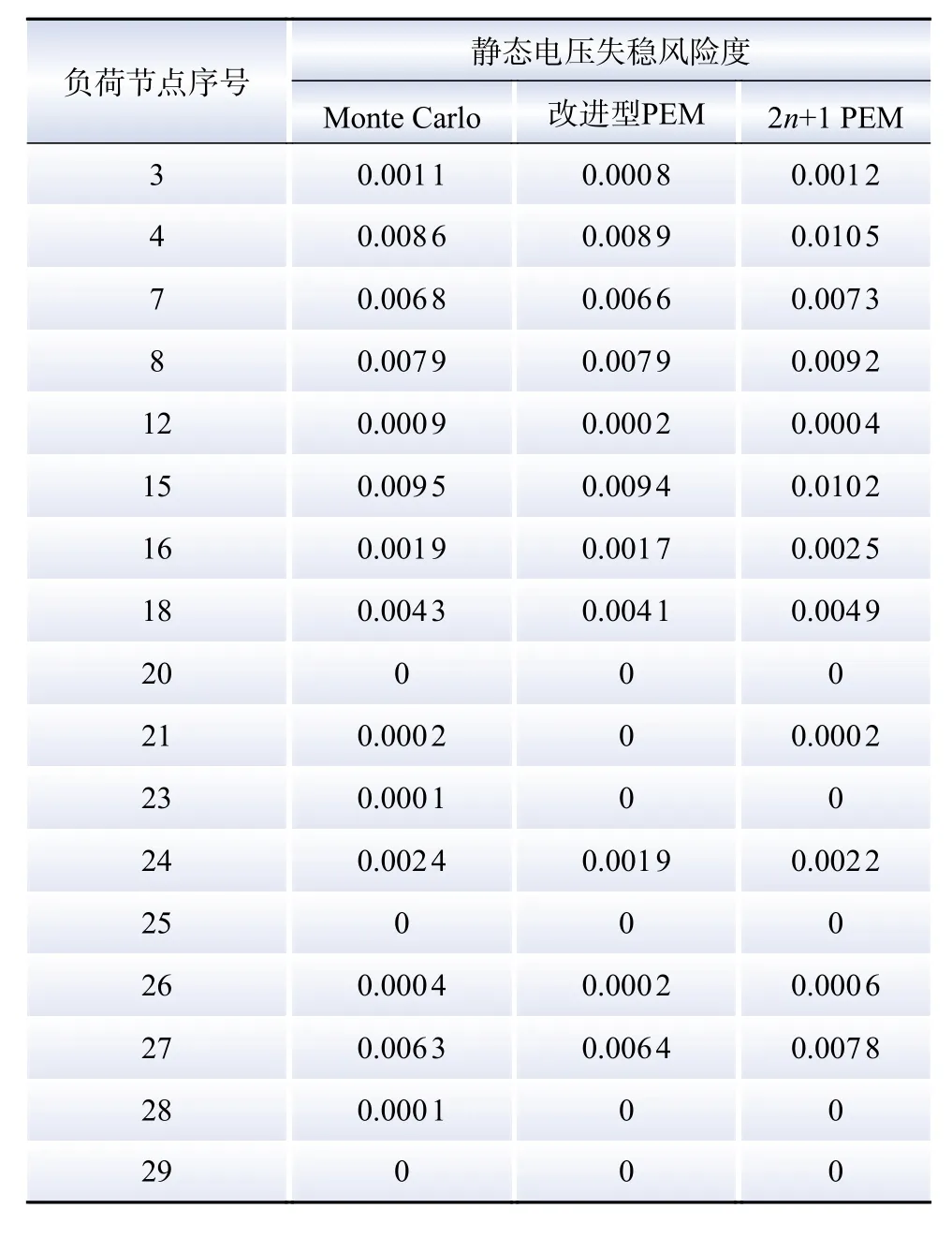
表3 改进IEEE-39节点系统中负荷节点电压失稳风险度Table 3 Risk of voltage instability of each load node in the improved IEEE-39 node system

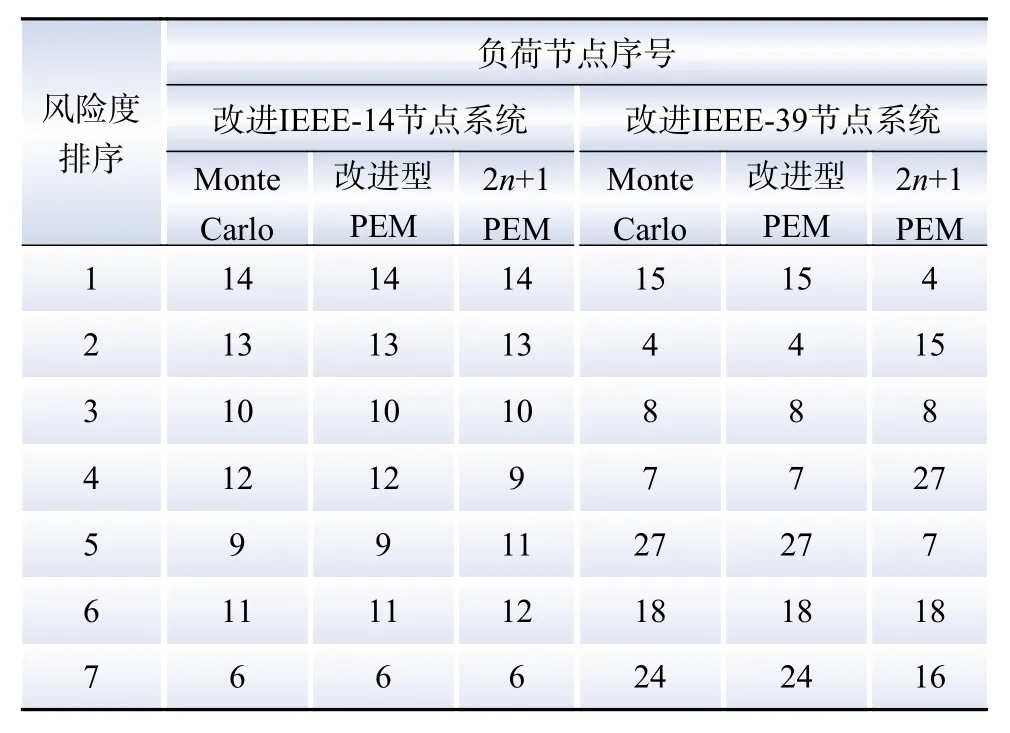
表4 负荷节点静态电压失稳风险度排序结果Table 4 Ranking results of the risk of steady-state voltage instability of load nodes

由表4可知，在IEEE-14和39节点系统中，由改进型PEM计算得到的静态电压失稳风险度排序结果与Monte Carlo法均是一致的；2n+1法虽然能识别系统中电压稳定风险度较为突出的部分节点，但具体排序结果与Monte Carlo法存在偏差。结合表2和3不难发现，2n+1法计算的风险度水平相比于Monte Carlo法普遍偏高，究其原因是其拟合L指标分布存在较大误差。显然，若L指标分布的拟合效果越优，电压失稳风险度的计算结果和薄弱节点的识别也就越准确。

4.4 风电并网对系统静态电压稳定性的影响

本节以上述改进的IEEE-14节点系统为例，结合3.3节中所提稳定因子λ研究风电并网后对系统静态电压稳定的影响。

根据式（28）和4.2节分析结果，系统的静态电压失稳风险度可取为节点14，即Rs=R14。以风电场1为例，将其用常规机组(cosφ=0.9)替换后，计算不同容量替换下的系统静态电压失稳风险度，结果如图7所示。

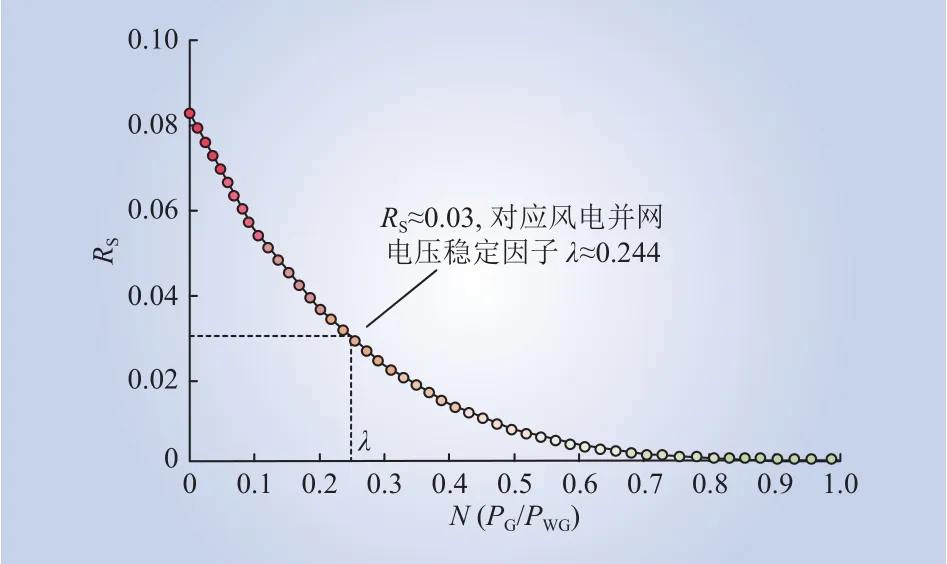
图7 不同常规机组替换容量下的RsFig. 7Rsunder different conventional unit replacement capacity

在上述风电场以cosφ=1并网条件下，由图7可知，当N=0时，系统静态电压失稳风险度高于风电并网后的水平，说明上述风电场1的并入对系统静态电压稳定性有一定的提升作用，这是由于此时风电作为纯有功电源接入后改善了潮流分布；当N=1时，风险度低于风电并网后的水平，说明这种改善效果达不到等容量常规机组的贡献水平，这主要是因为风速的随机波动性使得风电场实际有功出力难以达到其装机容量水平。由图7知该定义下的稳定因子λ为0.244左右。

此外，考虑到系统电压稳定通常与无功关系密切，上述研究中均认为并网功率因数为1，下面将改变风电场1的并网功率因数来计算其稳定因子变化情况。

图8给出了不同并网功率因数下稳定因子λ的变化情况，可以看出随着并网功率因数的减小，λ逐渐降低。当功率因数达到0.84左右时λ变为0，这意味着此时风电并网对系统静态电压稳定几乎不产生影响，说明了此时风电作为有功电源对系统静态电压稳定性的提升效果与作为无功负荷对系统静态电压稳定性的降低作用相抵消。若并网功率因数继续降低，则风电场向系统吸收的无功显著增加，稳定因子λ将出现负值，说明此时风电的并入将对系统静态电压稳定产生不利影响。由此可推断对于并网型风电场，存在某个临界水平的cosφ，使得其并网后对系统静态电压稳定的影响为零，而本文研究算例中的风电场临界cosφ即为0.84左右。

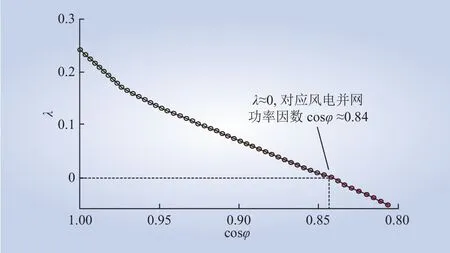
图8 不同并网功率因数下的λFig. 8λunder different grid-connected power factors

从上述分析可以看出，风电的有功电源特性对系统静态电压稳定性的提升作用非常有限且随着并网功率因数的降低这种作用被迅速抵消，而若能控制并网功率因数在相应的临界水平以上就可保证其稳定因子λ≥0，即不会对系统静态电压稳定造成负面影响，这也就要求大规模并网型风电场须配备充足的无功补偿装置。

5 结论

本文提出了一种基于改进型PEM和L指标的含风电场电力系统静态电压稳定评估方法，主要完成工作和所得结论如下。

（1）提出了一种用于系统静态电压稳定评估的改进型PEM，与Monte Carlo法的结果对比验证了该方法可以提升L指标分布的拟合精度；

（2）结合效用函数理论计算电压失稳风险度，完成了含风电场电力系统静态电压稳定评估，准确有效地识别了系统中存在的电压薄弱节点；

（3）引入风电并网电压稳定因子，实现了风电并网对系统静态电压稳定影响的量化分析，简洁直观地说明了风电场配备充足无功补偿装置的必要性，可为电力系统规划与运行提供一定的参考。

最后需要指出的是，本文研究中认为风电场配备了一定无功补偿装置，将风电场简化为PQ节点来处理，而实际中并网风电场无功电压有多种控制模式，不同控制模式可能会对本文计算结果产生一定影响，后续将围绕此开展进一步研究。