基于双侧电压反馈控制策略的并网光伏系统电压稳定性研究
薛飞,李旭涛,李宏强,田蓓
(国网宁夏电力有限公司电力科学研究院,宁夏 银川 750001)
0 引言
光伏系统将光能转化为电能,光照量的随机性导致其输入功率也具有随机性[1-2],两级光伏系统的前级变流器一般只具有最大功率跟踪(maximum power point tracking,MPPT)功能[3-4],无法对直流母线电压进行稳定调控,这种情况下,如果电网发生电压突变,将导致功率波动被传递到直流母线电容上,导致直流电压突升[5];加之,配电网故障也会传递到光伏系统,而直流电压往往通过并网逆变器的电压反馈进行控制,如果并网点电压发生突变[6],而电流内环无法快速对故障进行反应,将导致控制环路饱和,电压环无法有效跟踪参考值,进而致使直流电压突升,直流电压波动进一步恶化,最终导致光伏系统无法正常运行甚至脱网[7]。因此,有必要对现有控制策略进行改进,以提高光伏系统在多种扰动工况下直流电压的稳定性。
国内外学者针对光伏系统电压稳定性进行了大量研究。文献[8-10]将电压反馈引入逆变器控制中,实现了光伏直流系统电压的稳定控制,但未涉及并网电压突变时直流母线电压随之波动的研究;文献[11]提出的灵活功率跟踪算法(flexible power point tracking,FPPT)通过动态更改直流电压参考值,提高了低电压穿越(low-voltage ridethrough,LVRT)时直流电压的稳定性,但需要引入直流电压对电网电压的跟踪算法,算法的复杂度较高;文献[12-13]通过反馈并网电压到前级变流器对光伏板进行直接功率控制,并在前级电路中引入直流电压的反馈环节,对直流电压进行间接控制,该方法不仅能实现对中间直流电压的稳定控制,还能省去直流电容的采样电路,但其控制逻辑复杂、计算量大,对控制系统的硬件要求高;文献[14]提出了改进占空比调制法,有利于两级光伏系统的母线电压稳定运行,但计算量较大,对控制器的采样精度和计算速度要求更高;文献[15]将附加功率环路引入逆变器控制中,提高了功率波动下电压的调控能力,但未探讨电压穿越时逆变器对直流电压的调控能力;文献[16]将比例-谐振(proportion resonant, PR)控制与LC型滤波结合,形成软-硬件双回调控策略,提高了光伏系统的鲁棒性,但PR控制对非设定频率的故障或扰动响应特性较差,而电压穿越可能使并网点频率发生变化,导致上述策略失效;文献[17]提出了一种改进的电流反馈和电压前馈控制策略,能有效对交流小扰动进行稳定调控,但在面对电压穿越等大扰动故障时,该方法依然无法保证直流系统的稳定运行。
综上,现有研究大多从逆变器角度对并网光伏直流系统进行稳定控制,鲜有关注前级升压电路对直流系统电压稳定控制的潜在价值。本文提出一种双侧电压控制策略,在电压穿越情况下,光伏系统不仅能够充分利用后级并网逆变器对直流电压进行调控,还能利用前级升压电路的混合控制策略对直流母线进行自适应调控,进而提高光伏系统在低电压穿越时的安全稳定运行能力。
1 光伏系统结构
图1为光伏系统的典型结构示意[18-19],光伏板将光能转化为电能,通过Boost电路进行升压变流,并输出稳定的直流电压(施加在母线电容上),并网逆变器将稳定的直流电压变流为交流电压,并与交流电网进行并网。
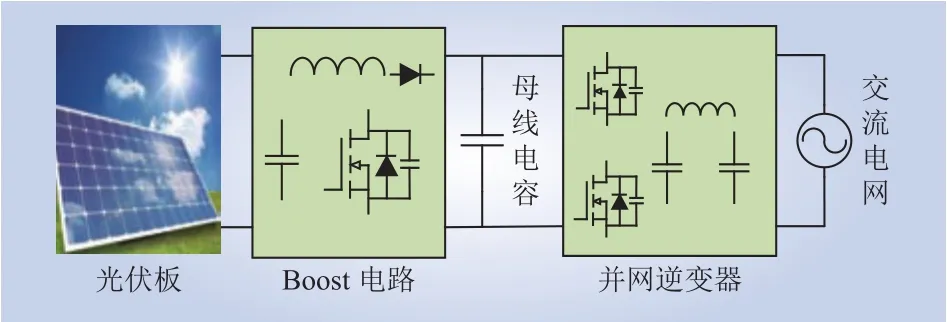
图1 并网光伏系统结构Fig. 1 Structure of gird-connected photovoltaic system
图2为Boost变流器级联H桥逆变器构成的典型光伏系统电路。图中:ip、up分别为光伏板的输出电流和电压;Cp、Cd分别为Boost变流器的输入侧和输出侧滤波电容;ud为Cd的电压;S1—S5为高频开关器件;L为Boost变流器的升压电感;ug为电网电压;ig为并网电流。
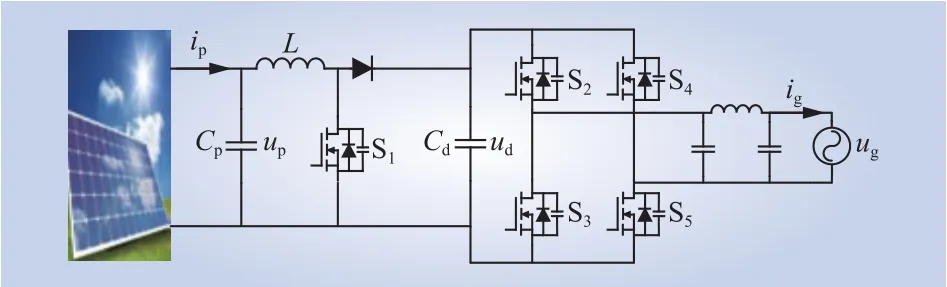
图2 并网光伏系统电路Fig. 2 Circuits of grid-connected photovoltaic system
2 双侧电压反馈控制策略
2.1 传统控制策略
光伏板的等效电路如图3所示[20],图中:Dp、Rs和Rp分别表示PN结、串联电阻和并联电阻;ih、id、ip和ipv分别为光生电流、PN结电流、并联电流、输出电流;upv为输出电压;Ro为负载等效电阻。根据电路原理,当Ro等于光伏板内阻时,光伏板输出最大功率Pmax[21]。
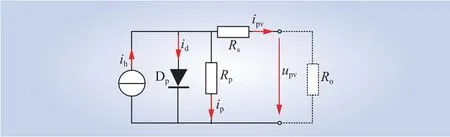
图3 光伏板等效模型Fig. 3 Equivalent model of photovoltaic panel

以江苏正信公司型号为ZXP6-60-250 P的光伏板为例,其最大功率Pmax=250 W,最大工作电压Umax=30.15 V,最大工作电流Imax=8.29 A,开路电压Uoc=37.89 V,短路电流Isc=8.61 A,可得到如图4所示的ppv~upv关系曲线,当upv=Umax时,光伏板输出最大功率Pmax=250 W。

图4 光伏板ppv~upv曲线Fig. 4 Curve of photovoltaic panel’sppvandupv
图5为前级升压变流器的传统控制策略,图中:Rinv为并网逆变器的等效负载电阻;p1为S1的控制信号;Up,ref、Ip,ref分别为up和ip的参考信号;v1为p1的调制信号。首先根据up和ip计算Up,ref,并将Up,ref和up的差值输入电压控制器1得到Ip,ref,Ip,ref和ip的差值输入电流控制器1,得到调制信号v1,v1与脉冲宽度调制(pulse width modulation,PWM)模块中的载波信号相比较得到p1。通过调节p1使光伏板始终处于最大功率工作点[22-23]。
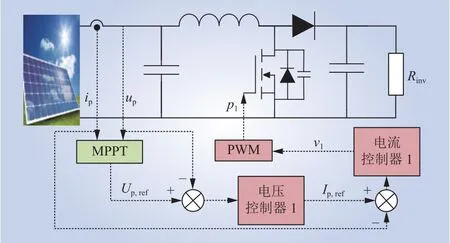
图5 前级电路的传统控制策略Fig. 5 Conventional control strategy of front circuits
图6为并网逆变器的传统控制策略,锁相环PLL通过ug计算并网电压相位θ,Ub,ref为ub的参考信号,电压控制器2的输出值与sinθ相乘得到电网电流ig的参考信号Ig,ref,v2为逆变器的调制信号,v2与PWM模块的载波信号相比较得到开关器件S2—S5的控制信号p2~p5。并网逆变器通过电压控制器2和电流控制器2同时对ub和ig进行反馈控制。

图6 并网逆变器的传统控制策略Fig. 6 Conventional control strategy of grid-connected inverter
由图5和图6可知,光伏系统对ub的调控仅能通过逆变器实现,而Boost变流器无法对ub进行调控。电流环和电压环均采用PI控制器,电流控制器1的比例和积分参数分别为kc1,p和kc1,i,电流控制器2的比例和积分参数分别为kc2,p和kc2,i,电压控制器1的比例和积分参数分别为kv1,p和kv1,i,电压控制器2的比例和积分参数分别为kv2,p和kv2,i。当逆变器达到稳态时,可认为Ig,ref与ig无误差,此时,ub与ig的关系可表示为
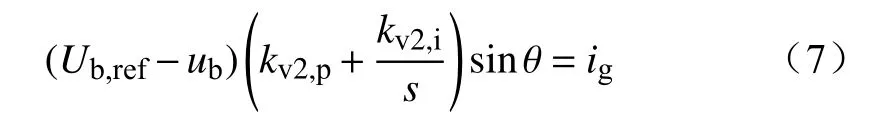
进而可求解出ub为

由于ig=Ig,pksinθ,Ig,pk为并网电流的峰值,并网功率Pg=IgUg,Ig和Ug分别为ig和ug的有效值,因此,式(8)的时域形式为

图7展示了当Ub,ref=400 V、Pg=100 W、Ug在t=0.5 s从220 V突降至44 V时ub的变化曲线,可以看出,电压控制器2的比例参数Kv2,p越小,ug发生穿越时,ub的冲击越大。当Kv2,p=0.8时,ub的冲击值为409 V;当Kv2,p=0.5时,ub的冲击值为424 V;当Kv2,p=0.8时,ub的冲击值为465 V。因此,当ug发生低电压穿越时,为了减小ub的冲击可将Kv2,p设为较大值。

图7 不同比例参数下低电压穿越时ub的变化曲线Fig. 7 Curves ofubduring LVRT under different ratio parameters
图8展示了Kv2,p=0.3、Kv2,i=10、Pg=100 W、Ub,ref=400 V时,Ug在t=1.0 s从220 V突降至44 V,并在t=1.7 s从44 V恢复到220 V时ub的仿真波形。忽略由于积分环节引起的震荡效应,仿真结果中,ub的变化趋势基本与图7中的解析分析结果一致,进一步说明传统控制策略下,电网发生低电压穿越故障时,会在直流系统中引起电压冲击,危及光伏系统的稳定运行。仿真结果的冲击峰值略低于解析分析结果的冲击峰值,这是由于系统存在阻尼。

图8 低电压穿越时ub的仿真曲线Fig. 8 Simulation curve ofubduring LVRT
2.2 双侧控制策略
为了避免交流电压故障对直流母线的冲击,提出一种双侧控制策略,给升压电路的MPPT控制环路引入并联电压环路,形成光伏侧电压控制;并保留逆变器的电压反馈控制环路,同时在光伏侧和网侧对直流电压施加闭环控制。
双侧控制策略的原理如图9所示,逆变器侧的控制与传统控制策略一致。不同于传统控制策略,为了提高控制系统在故障时对ub的调控能力,在升压电路的控制环路上并联ub的反馈回路。根据ip和up计算光伏的参考电压Up,ref,Up,ref与up的差值输入电压控制器1,经过电压控制器1的调节和增益为k1的放大器的作用,得到电流ip的参考信号Ip,ref,1;同时,将Ub,ref与ub的差值输入电压控制器3,并经过增益为k2的放大器的作用,得到ip的参考信号Ip,ref,2。需要注意的是,传统控制策略下,ip的参考信号等于Ip,ref,1,但在改进的双侧电压反馈控制策略下,ip的参考信号Ip,ref为
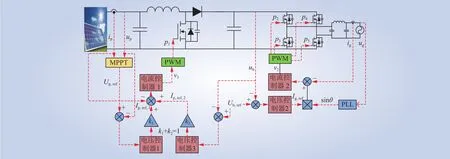
图9 双侧电压反馈控制策略原理Fig. 9 Principle of double-side voltage feedback control strategy

Ip,ref与ip的差值输入电流控制器1,得到调制信号v3,v3与PWM模块的载波信号相比较,得到升压电路的控制信号p1。k1和k2的取值范围均为[0,1],且k1+k2=1,k1值越大,k2值越小。k1较大时,控制器对up的调控能力高于对最大功率的追踪能力;k1较小时,控制器对最大功率的追踪能力强于对up的控制能力。为了提高系统的性能,对k1和k2的取值进行动态设计。当光伏系统稳定运行时,为了实现光伏功率的高效利用,取值k1>k2≥0,且k1接近1,使升压电路更偏重于MPPT控制;当ug发生急剧波动时,为了防止ub发生电压过冲,取k2>k1≥0,升压电路更偏重于对ub的稳定控制。



图10给出了传统控制下仿真波形。稳态时,ub、ug、ig、pg和ppv分别为 400 V、311 V、7.6 A、1 178 W和1 182 W。t=1.405 s时,发生低电压穿越,Ug的值从220 V跌落到44 V,并在t=1.88 s时逐渐恢复至220 V。
低电压穿越发生后,ub突升,穿越0.07 s后,ub达到最大值462 V,并在t=1.6 s时达到稳态,稳态值为446 V。ig在低电压穿越后也发生冲击,在t=1.54 s时达到最大值25.3 A。电网功率pg在低电压穿越后也发生冲击,在t=1.54 s时达到最大值3 924 W并维持到t=1.88 s,然后逐渐回降。光伏输出功率ppv在低电压穿越后发生跌落,当t=1.48 s时,达到最低值572 W,然后逐渐上升到830 W。从图10中,可明显观察到低电压穿越时光伏功率、并网功率、直流电压和交流电流均发生了冲击。直流电压甚至冲击到462 V,超过额定值的15.4%,导致直流电容承受过电压,如果采用Chopper进行功率吸收,将导致Chopper电阻过热,影响系统的安全稳定运行。
图11为采用双侧电压控制策略,且ub,up,lim=420 V时的仿真波形,当t=1.405 s时,Ug从220 V跌落到44 V,当t=1.88 s时,Ug从44 V逐渐恢复到220 V。ub在t=1.41 s时达到最大值421 V并维持在此值,ub在t=1.91 s时达到最小值328 V,ig在t=1.75 s时达到最大值25.0 A,pg在t=1.75 s时达到最大值3 900 W并维持0.02 s,ppv在t=1.43 s时达到最小值320 W。相比于图10,图11的功率冲击更小,ub的冲击也更小,主要原因是在低电压穿越时,双侧控制可以有效地降低光伏的输出功率,防止ub产生剧烈冲击。
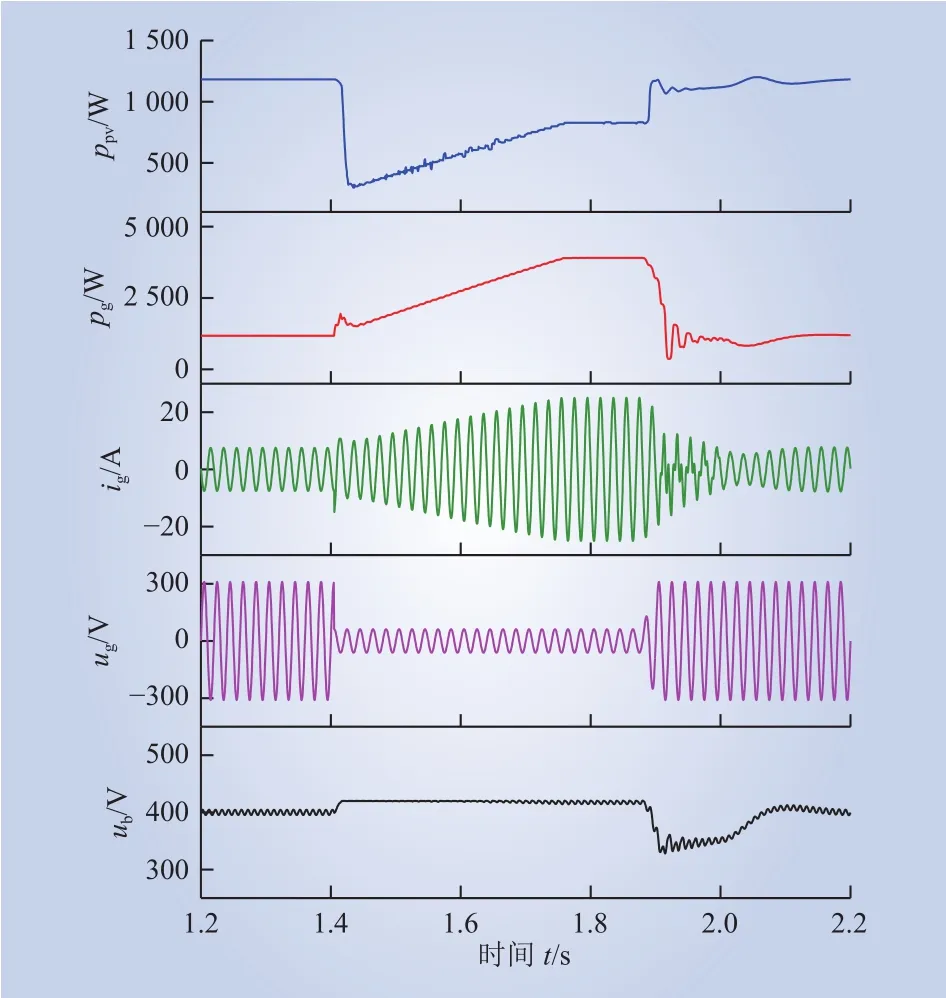
图11 双侧控制下ub,up,lim=420 V时的仿真波形Fig. 11 Simulation waveforms under double-side control withub,up,lim= 420 V
图12为当ub,up,lim=405 V时的仿真波形,当t=1.405 s时,Ug从220 V跌至44 V,当t=1.88 s时,Ug从44 V逐渐恢复到220 V。ub在t=1.41 s时达到最大值407 V并维持在此值,ub在t=1.94 s时达到最小值346 V,ig在t=1.87 s时达到最大值14.86 A,pg在t=1.88 s时达到最大值2 309 W,ppv在t=1.43 s时达到最小值260 W。相比图11,图12中pg、ig和ub冲击更小,这是因为低电压穿越时升压电路能更早介入电压和功率之间的协调控制,减小光伏阵列的功率输出,从而达到降低ub、pg和ppv冲击的目的。

图12 双侧控制下ub,up,lim=405 V时的仿真波形Fig. 12 Simulation waveforms under double-side control withub,up.lim= 405 V
3 实验验证
为了证实双侧电压反馈控制策略在提高光伏系统电压稳定性上的作用,基于图13所示的RTLAB半实物仿真平台进行了并网光伏系统的动态测试实验。测试系统采用的型号为ZXP6-60-250 P的光伏板参数,Pmax、Umax、Imax、Uoc和Isc已在前文中给出。

图13 RT-LAB 半实物测试平台Fig. 13 Hardware-in-loop test based on RT-LAB platform
光伏阵列采用5块光伏板串联结构,表1为光伏系统的相关参数。

表1 光伏系统参数Table 1 Photovoltaic system parameters
图14为传统控制策略下,当Ug发生20%电压跌落并持续0.475 s情况下,ub,ac、ug、ig、pg和ppv的硬件在环测试测试波形,仿真模型的阻尼作用及电压探头的带宽影响会导致测试结果(图14)与仿真结果(图10)之间存在一定的误差,主要体现在电压穿越起始和截止过程中,但不影响本文控制方法验证结果的合理性和正确性。

图14 传统控制下低电压穿越时的波形Fig. 14 Waveforms during LVRT under conventional control
当Ug从220 V跌落到44 V后,ub,ac经过0.06 s上升到62 V,并在t=1.58 s时稳定在46 V,当Ug在t=1.88 s恢复电压跌落后,ub,ac经过35 ms从0 V下降到最低值-74 V,在低电压穿越期间,ub,ac的变化量为136 V,约为Ub,ref的34%。光伏功率ppv在电压跌落发生47 ms后,从1 182 W下降到590 W。并网功率pg在电压跌落发生0.17 s后由1 177 W上升到3 955 W,为额定功率的3.36倍。ig的峰值在电压穿越过程中从7.8 A上升到28.6 A,是额定并网电流的3.67倍,如果不设置Chopper电阻并投入使用,大电流应力将可能使逆变器发生过热损坏,而在光伏系统中设置大功率Chopper电阻不仅会增加系统的硬件成本,还会带来散热问题。
图15所示为改进双侧电压控制下光伏系统的测试波形,为了对比实验的公平性,双侧控制的实验条件设置与传统控制策略相同。在ug发生跌落并恢复的过程中,ub,ac的最大值和最小值分别为6.5 V和-54 V,ub,ac的变化量为60.5 V,约为Ub,ref的15.1%,ig的峰值为14.6 A,pg在跌落0.475 s后达到最大值2 264 W,ppv在跌落75 ms后达到最低值272 W。
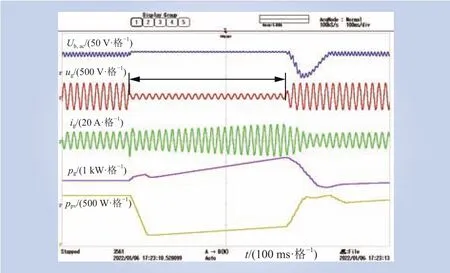
图15 双侧控制下低电压穿越时波形Fig. 15 Waveforms during LVRT under doubleside control
表2给出了2种控制策略下光伏系统低电压穿越的测试对比情况。由于改进的双侧控制策略能在低电压穿越前期将双侧电压控制引入光伏系统,通过改进控制策略,利用升压电路降低光伏的输出功率,从而实现在低电压穿越时对ub的快速稳定调控,降低ub在低电压穿越时的波动范围,将电压波动量Δub,ac从136 V降低到60.5 V,将直流母线电压波动率α从34.0%降低到15.1%。测试对比结果显示,改进的双侧电压控制策略能够在低电压穿越时提高光伏系统直流电压的稳定性。
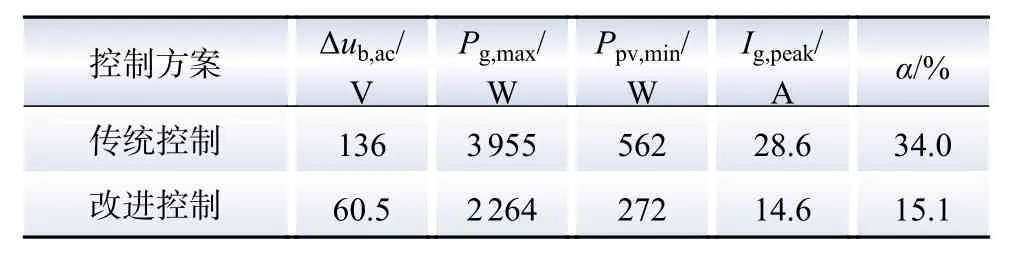
表2 低电压穿越测试对比Table 2 Comparison of low voltage ride through tests
4 结论
针对光伏系统在低电压穿越时容易产生功率冲击并将冲击传递到直流母线的问题,本文提出了一种双侧电压控制策略,在不设置Chopper电阻的情况下,基于RT-LAB平台搭建的半实物实验结果证实了改进的双侧电压控制策略能降低电压穿越时并网光伏系统直流母线电压的波动幅值及并网功率的冲击值,提高光伏系统的稳定运行能力。

