基于运行优化的含储能电力系统可靠性评估方法

张黎明，李浩，吴亚雄，高崇，张俊潇，刘涌

(1. 广东电网有限责任公司 电网规划研究中心，广东 广州 510080；2. 上海博英信息科技有限公司，上海 200240)

0 引言

随着分布式电源（distributed generation，DG）、储能不断并入电网，配电网潮流逐渐转变成双向潮流[1-3]。DG容易受环境因素影响，其出力存在间歇性和不确定性。传统可靠性评估方法主要适用于中压配电网，在双碳背景下，新型电力系统亟需新的可靠性评估方法。

文献[4-15]建立了DG出力的概率模型，并通过抽样形成DG出力的时序曲线。文献[16-18]提出概率可靠性评估方法，探讨了随机波动对系统可靠性的影响。文献[19-25]准确区分了故障后的孤岛负荷以及故障区负荷，其中岛内负荷可以由DG继续供电。文献[20]提出了以DG为中心的区域供电模式和功率匹配策略，其根据事先划分好的供电区域进行系统内功率划分，但功率匹配没有达到最优。文献[21]通过广度优先搜索算法得到最大的孤岛范围以确保较小的停电损失，但该方法没有考虑多个有源元件接入不同位置导致的孤岛间重合问题。

本文提出考虑运行优化的新型电力系统可靠性评估方法。基于拓扑的故障隔离方法，根据故障位置、拓扑结构细化故障隔离区域。同时，在故障隔离范围引入考虑网络重构的运行优化方法。采用序贯蒙特卡洛模拟法进行系统可靠性分析。

1 新型电力系统元件概率模型

风电机组功率主要取决于风速的大小。风速一般服从威布尔概率分布，其中c和k为威布尔概率分布的形状、尺度参数。实时风速与风电机组输出功率PWT之间的关系为

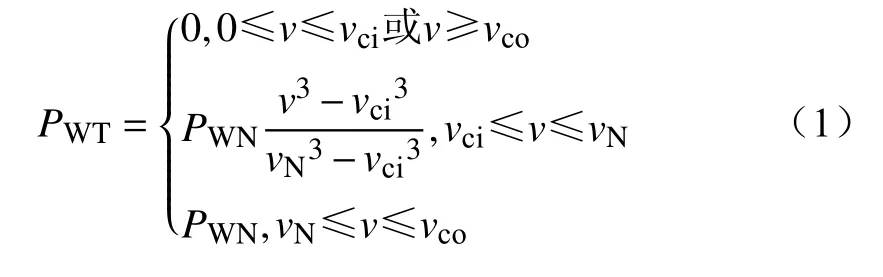
式中：v、vN、vci、vco分别为实际风速、额定风速、切入风速、切出风速；PWN为机组额定功率。

光伏机组出力取决于光照强度。光照强度近似服从Beta分布，α和β分别为Beta分布的形状参数。光伏机组的出力PPV与光照强度E之间的关系为

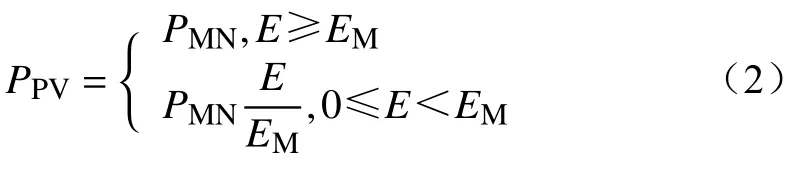
式中：PMN为光伏额定功率；EM为光照强度饱和值。

分时电价机制如图1所示。储能电池荷电状态（state of charge，SOC）变化曲线如图2所示，其中Smax、Smin分别为储能的最大、最小SOC；分别为储能的最大充、放电功率；S(t)为时刻t储能SOC的期望值。要保证在系统故障时有较多剩余电量且实现利益最大化，本文制定的策略为：在谷段以最大充电功率充电，在谷段前的平段不充电，其余平段以最大充电功率充电。同一峰段或尖峰段内，以同样的功率放电，力求本峰段放电电量最大。与此同时，考虑到随机充放电因素的影响，本文参考文献[21]对储能SOC进行随机建模。

图1 分时电价机制Fig. 1 Time-of-use price mechanism

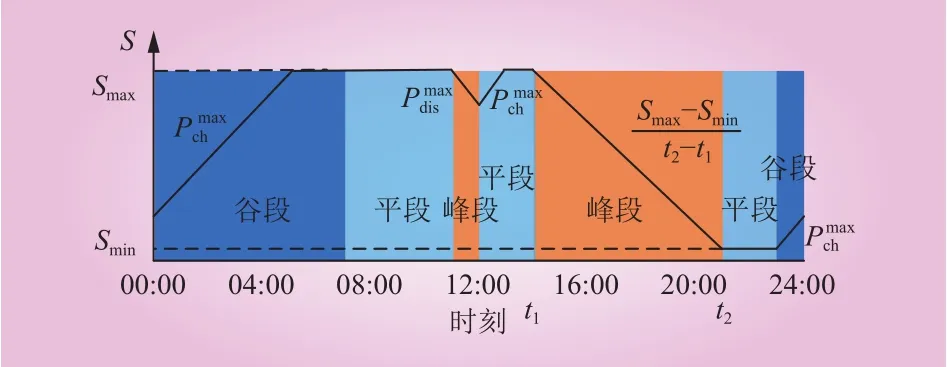
图2 储能SOC变化曲线Fig. 2 Curve of energy storage SOC

2 可靠性评估方法

在故障隔离中，本文根据主馈线上的断路器将系统分为不同主区域，并基于隔离开关的位置，将各区域再细分成不同的子区域。主馈线和负荷支路发生故障的一次故障隔离范围为所处主区域除内部电源部分。电源支路发生故障的一次故障隔离范围为发生故障的电源支路。一次故障隔离会造成大量负荷失电，因此系统需要根据故障位置重新判断故障隔离范围，进行二次故障隔离。主馈线和负荷支路故障时的二次故障隔离范围为故障所处的子区域。电源支路故障没有二次故障隔离问题。

2.1 故障后系统运行优化模型

本文采用考虑网络重构的运行优化方法对故障隔离范围外的系统进行孤岛划分和功率匹配，从而减少失电范围。在故障隔离过程中，每次拓扑改变后均考虑网络重构的运行优化，即在非故障范围进行孤岛划分和功率匹配，优先保障重要负荷供电，减少失电影响。馈线分区示意如图3所示。为方便表述故障区域，在图3中用红点表示断路器和隔离开关两端增加的节点，用黑点表示每条支路通过相应节点接入的主馈线。

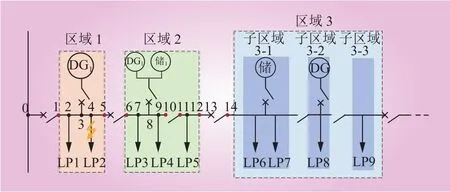
图3 馈线分区示意Fig. 3 Schematic diagram of feeder zone

故障后的系统运行优化目的为系统失负荷影响最少，则本文的目标函数为

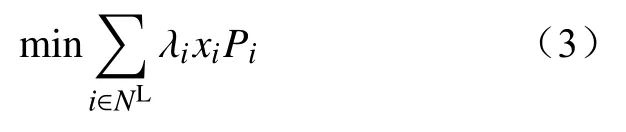
式中：i为节点编号；NL为负荷支路节点的集合；xi为节点i处切负荷的变量，其中0表示切除负荷，1表示不切除负荷；Pi为节点i所连接支路的功率；λi为节点i处负荷的重要性系数。

目标函数对应的功率平衡约束为

式中：M为同节点i相邻节点的集合；Nall为系统所有节点的集合；Pij为节点i到j的传输功率。

主馈线有一定传输功率限制，即

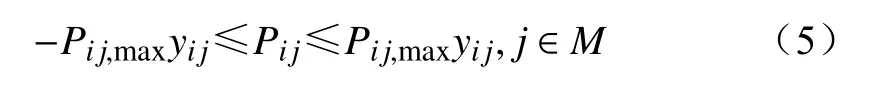
式中：Pij,max为节点ij间的最大传输功率；yij为节点ij间是否有功率流动的状态变量，其中0表示无功率流动，1表示有功率流动。

若节点ij之间没有断路器和隔离开关，直接通过导线连接，其功率流动状态由节点ij是否处在故障隔离范围确定；若节点ij之间有断路器和隔离开关，其功率流动状态由断路器或隔离开关的闭合和断开状态决定，即

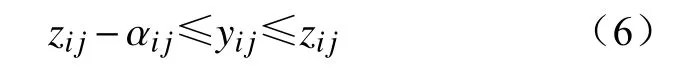
式中：zij为节点ij是否处在故障隔离范围的状态变量，其中0表示处在故障隔离范围，1表示未在故障隔离范围；αij为节点ij是否通过断路器或者隔离开关进行连接的状态变量，其中1表示节点通过断路器或者隔离开关相连，0表示未相连。

2.2 影响分析及可靠性评估流程

对于故障隔离区域内的负荷，如果系统只发生一次故障隔离，则故障隔离区域内的负荷停电时间为故障元件修复时间。如果系统发生两次故障隔离，那两次皆位于故障隔离范围的负荷停电时间为故障元件修复时间。只有第一次位于故障隔离范围，第2次不在故障隔离范围的负荷失电时间不少于故障隔离与网络重构时间。

对于不位于故障隔离区域的负荷，若负荷始终不位于故障隔离区域，则负荷停电时间等于切负荷时间；若负荷曾经位于故障隔离范围，其后离开故障隔离范围，则负荷停电时间等于故障隔离与网络重构时间加切负荷时间。故障隔离与网络重构优化流程如图4所示，其中tout为负荷停电时间；Tf为故障隔离与网络重构时间；Tr为故障元件修复时间。

本文采用基于序贯蒙特卡洛模拟法进行可靠性评估，具体步骤如下。

（1）输入配电网拓扑、用户数、储能参数等与可靠性评估有关的原始数据。

（2）根据DG、储能、负荷历史数据结合对应的概率模型获得相应时序功率曲线。

（3）计算元件m正常工作持续时间和故障修复时间。

（4）将所有元件中最小的正常工作持续时间设为系统的正常工作持续时间，并累加仿真时间。

（5）基于故障后系统运行优化模型得到负荷停电情况。通过负荷停电次数和时间确定系统停电损失。

（6）重复步骤（2）～（5）直到达到设定的仿真时间。

（7）计算负荷点可靠性指标和系统可靠性指标。

3 案例分析

本文以改进IEEE RBTS Bus6的F4主馈线为算例进行可靠性分析。其中DG风机额定功率为1 MW，形状、尺度参数分别为13.16和3.76。储能额定容量为1 MW·h，额定功率为0.16 MW。负荷功率预测误差期望为0 MW，标准差为0.005 MW。通过本文方法可以得到IEEE RBTS Bus6的F4主馈线的可靠性指标，其中系统供电可靠率为99.53%。

目前，系统中的有源元件主要包括DG和储能。有源元件的参数将对系统可靠性产生一定影响。分析DG渗透率对系统可靠性的影响，如图5所示。在图5中，红点为不同DG额定功率下的系统缺供电量，蓝线为三阶Hermite插值。由图5可见，随着DG功率的增加，系统缺供电量减少。当系统发生故障后，以非故障隔离区域DG为主要电源形成孤岛，减少了负荷失电。同时随着DG额定功率增加，系统缺供电量的下降幅度呈现变小趋势，故当DG额定功率达到一定值时，通过增加DG功率提高可靠性的效果不佳，反而会造成较大的经济负担。

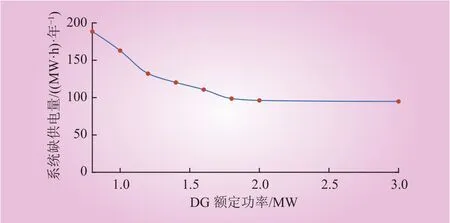
图5 DG渗透率对系统可靠性的影响Fig. 5 The influence of DG penetration rate on system reliability

分析储能功率和容量对系统可靠性影响。储能容量对系统可靠性的影响如图6所示。在图6中，2条曲线分别描述了储能充放电功率不变时，储能容量发生变化对系统缺供电量的影响以及储能充放电功率随储能容量等比例变化时，储能容量发生变化对系统缺供电量的影响。由图6可见，系统缺供电量随着储能容量变大而降低，即系统可靠性上升；当储能充放电功率不变时，系统可靠性随容量增大而上升的幅度较小；当储能充放电功率同比例变化时，系统可靠性随容量增大而上升的幅度较大。这是因为本算例中的储能原始充放电功率较小，即使增加储能容量，在停电时间较短的故障中储能对失电负荷的供电也有限。同时，随着储能容量的不断增加，可靠性上升幅度逐渐降低。通过配置储能提升系统可靠性时需谨慎选择储能容量。通过增加不同储能容量下边际停电损失收益如图7所示。

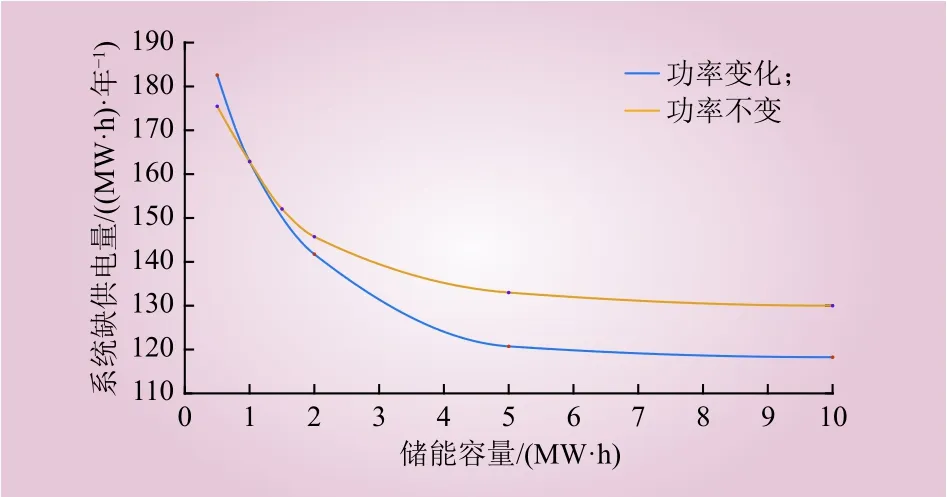
图6 储能容量对系统可靠性的影响Fig. 6 The influence of energy storage capacity on system reliability

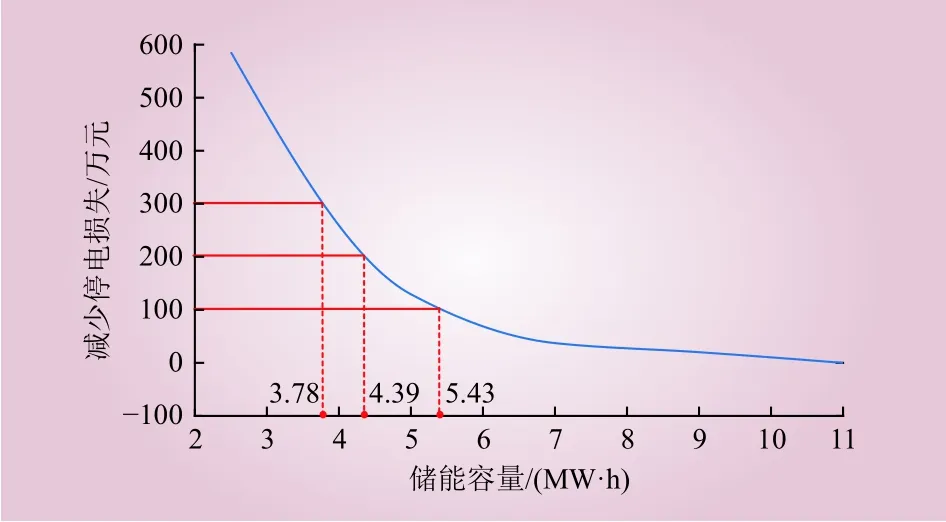
图7 不同储能容量下边际停电损失收益Fig. 7 Marginal outage loss benefit under different energy storage capacities

基于此算例，将故障后非故障隔离区域的DG和储能改为只为本供电区域内的负荷供电，则系统停电频率比原始算例增加了12.59%，停电时间增加了12.65%，供电可靠率降低了0.07%，缺供电量增加了6.68%。由此可见，故障隔离后的网络重构优化方案会直接影响系统供电可靠性，采取本文方法能使资源配置更合理，避免各个区域供电不平衡问题，从而提高了系统的供电可靠性。

4 结语

本文提出了基于运行优化的新型电力系统可靠性评估方法，对考虑网络重构的最优运行方案进行可靠性评估，在每次故障中根据故障隔离范围实时计算非故障隔离范围的失电情况，有利于减少故障后的失负荷影响，从而提升系统可靠性。通过算例分析可得，DG和储能参数可以影响系统可靠性。随着DG的额定功率和储能额定容量配置增加，系统可靠性增加，但增加幅度逐渐减小。因此，可以通过配置DG和储能增加系统可靠性，但须注意成本回报率。