用极课数据助力课堂精准教学
——以“相似三角形的复习课”为例
201799 上海市青浦区豫才中学 王 龙
201799 上海市青浦区实验中学 柳 雪
精准教学是教师根据课程标准、教材和学情,遵循学科教学规律,遵循学生成长规律和认知规律,聚焦课堂教学价值,准确把握教学目标和教学内容,构建科学的教学结构,细化教学流程,促进学生在“三维”目标上获得可持续的进步和发展,实现预期目标和完美的教学效果的活动过程.极课数据是基于教学的一种人工智能技术.在批改作业及试题后,通过图像识别仪扫描答题纸收集数据,并对数据库进行智能分析,辅助教师教学,为学生提供自适应学习资料,实现大数据管理教学和智能驱动的精准教学.复习课该怎样精准教学?复习课要教会学生什么知识?是将学过的知识点全面铺开,逐个复习一遍,还是针对某几个知识点专门研究学习?这些问题经常困扰一线教师.运用极课数据提供的信息可以精准了解学情,从而为学生量身定制复习方案,帮助教师抓住教学重点,改良教学内容,优化教学策略,弥补学生学习中的不足之处,从而提高学生的学业水平.在学生学习沪教版《数学》九年级第一学期第24章“相似三角形”后,笔者依据数据提供的信息,尝试开展一节复习课,发现利用极课数据实施精准教学具有以下优势.
一、精准解读学情,让教学目标更契合学生的学习需求
在传统的教学模式下,教师对学情的把握主要依据课堂观察与学生的作业和测试.基于课堂观察与作业得出的学情具有很大的主观性,教师视角下的学情与学生的实际情况存在较大差距.在大数据支持下,教师可以借助数据提供的信息,精确对比得到本班与其他班级之间的数据差异,精准了解学生对相关知识点的掌握情况,有效整合资源以确定教学目标与重难点.学生学习“相似三角形”后,分析极课数据提供的信息(如图1所示)可得,对于知识点“相似三角形的性质和判定”,班级得分率达到80.1%,比年级平均得分率低3.8%.与其他知识点相比,这一知识点得分率相对低了13%—17%.在相似三角形的综合应用方面,本班得分率更低,只有11.3%,比年级得分率相对低了4.6%.这表明知识学习出现漏洞,因此有必要针对相似三角形的判定与性质进行一次整理复习,弥补知识上的缺陷.
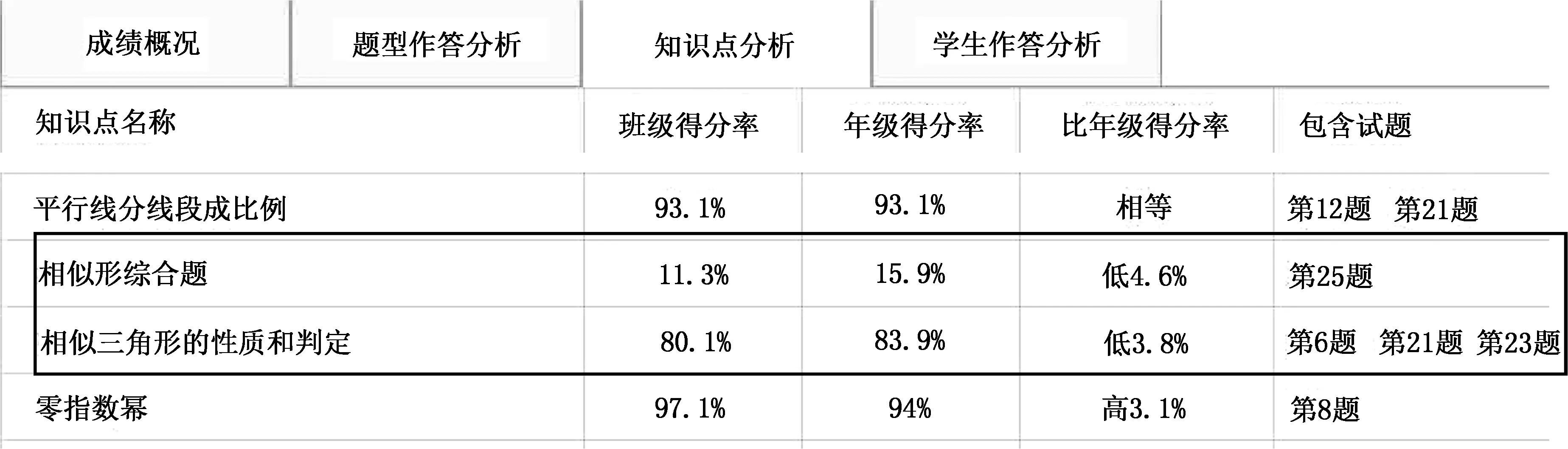
图1
相似三角形的判定及性质是几何知识中的重要内容,对培养学生分析、解决问题的能力,体会数学的价值有重要的意义.为此,设定了如下教学目标与重难点.
教学目标:
(1)熟悉几种常见的基本图形,会利用基本图形找相似三角形.
(2)通过对基本图形的探究与应用提升学生的思维能力与解题能力.
(3)在对基本图形的应用中体会化归思想,培养自主意识,激发探究数学的兴趣,感受几何知识的魅力.
教学重点:熟练运用基本图形,迅速找出复杂图形中的相似三角形.
教学难点:找到基本图形并运用本节课的知识解决问题,能够构造基本图形解决问题.
通过数据得到的学情能准确说明学生对相似知识掌握的情况,更符合学生的实际情况.以此学情为依据整合资源确定的教学目标,才是最符合学生实际学情的教学出发点.
二、精准锁定教学切入口,吻合学生认知出发点
教材是实施课程教学的载体,教师通常以教材为教学的出发点,组织学生进行学习.然而一节好的复习课往往没有教材与教参的支撑,教师往往对此感觉无所适从.惯用的复习方式是把所有的知识点罗列出来,再梳理一遍,这种常规的教学方法针对性不强、重点不突出,不适合学生的实际情况.经验丰富的教师会设计一些题组,通过题组复习知识点,这种复习方式也不能完美契合学生的学习需求.任何形式的教学最终都要回归到学生这一主体,只有复习方法与教学设计契合学生的需求,才能发挥其应有的价值.利用极课数据提供的信息(如图2所示)容易找到学生的知识薄弱点,从而锁定教学的切入口.

图2
由数据可知,学生对“相似三角形的判定及性质”掌握不扎实,班级得分率不到70%,比年级得分率低9.3%.这类问题要求运用基本图形,因而确定本节课以基本图形导入教学,教学行为由教学目标准确引导,设计出契合学情的教学流程和教学活动方案.
活动1再认识基本图形中的相似三角形
如图3-1-3-8,观察下列图形,找出图中的相似三角形.
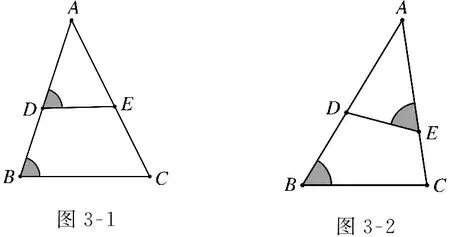
图3-1图3-2
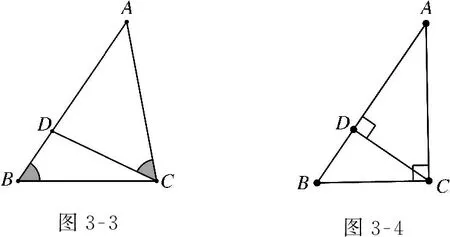
图3-3图3-4

图3-5图3-6

图3-7图3-8
设计说明:设计题组的目的是帮助学生认识这些共边或共角的基本图形.图3-1的特征是DE∥BC,常被称为“A型图”.图3-2类似于图3-1,但DE与BC不平行,被称为“斜A型图”.当DE向下平移到一端点与顶点重合时,就构成了斜A型图的特殊情况,如图3-3所示.当顶点重合的两个角中,有一个角为直角时,此时该模型中有三个直角三角形而且两两相似,因此该模型又被称为“母子型”,如图3-4所示.如图3-5,由一条平行于AB的直线截直线OA与直线OB得到的两个相似三角形图被称为“X型图”.在X型图的基础上,当AB与CD不平行时,被称为“蝶型图”,如图3-6所示.如图3-7、图3-8,可见两个既共边又共角的相似三角形,其特点是夹着公共角的两边也共线.要求学生记住这几个基本模型,熟悉几种常见的相似三角形,以此为本节复习课的突破口,之后再遇到这些基本图形时,能更容易找出其中的相似三角形,解决问题的效率会大幅提高,从而提高学生的高阶思维能力.
三、精准组织学生学习,分层探寻规律,提升学生分析问题的能力
在组织学生探究学习的过程中难免会遇到各种困难,课堂需要分层开展,让学生解决难度适合的问题.以学生为主体的现代教学理念要求学生多思考,多参与到教学中.常规教学方式下,教师提问后一般请举手的学生回答问题,或凭印象找适当的学生回答问题.但是这种教学方式存在弊端,如果只请举手的学生回答问题,学习交流的机会通常会被几位活跃的学生占据,其他学生只能当“观众”.凭教师的印象找学生回答难免会有遗漏,部分学生无法参与教学.在大数据的环境下,教师对学情的解读可以减少狭隘性、主观性,通过学生作业或者测试中的表现确定教学内容与教学侧重点.
如图4所示为极课数据提供的信息.信息表明班级中有8位学生得分在0-3分,对基本相似图形陌生,需要教师重点关注.有5位学生得分在3-6分,说明对基本图形的应用不熟悉,不能从复杂图形中找出基本图形,需要提升认知水平.得分不高原因在于复杂图形中斜A型图被隐藏,为排除干扰,需要从复杂图形中抽丝剥茧,剥离出基本图形.据此,教师设计教学活动2.

图4
活动2从复杂图形中找出相似三角形
题1如图5-1,在△ABC中,D,E在AC,AB边上,DE∥BC,则图中相似的三角形有哪些?
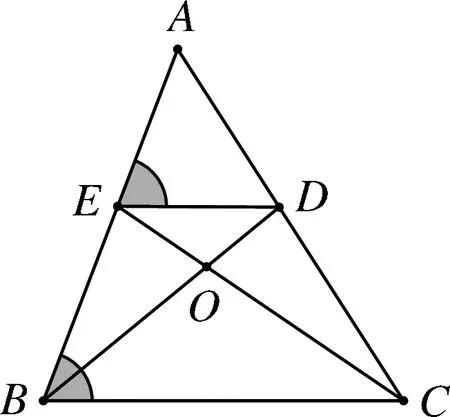
图5-1
题2如图5-2,在△ABC中,D,E在AC,AB边上,∠AED=∠ACB,则图中相似的三角形有哪些?
题3如图5-3,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,联结DE,则图中相似三角形有哪些?
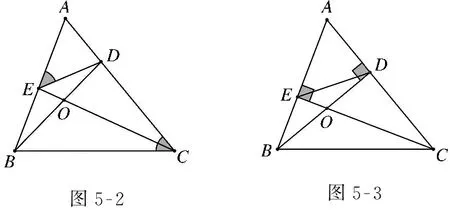
图5-2图5-3
设计说明:相对于活动1中的基本图形,活动2中的图形更为复杂,同一张图中可能隐藏两个或以上的基本图形.将图5-1与图5-2放在一起辨析,第1题的分解图如图6-1所示,第2题的分解图如图6-2所示.教师在组织教学时,可以让得分在0-3分的8位学生完成第1题和第2题,如果遇到困难,可以让得分在3-6分的学生进行补充,让每个层次的学生都能“跳一跳”摘到果实,品尝到成功的喜悦.
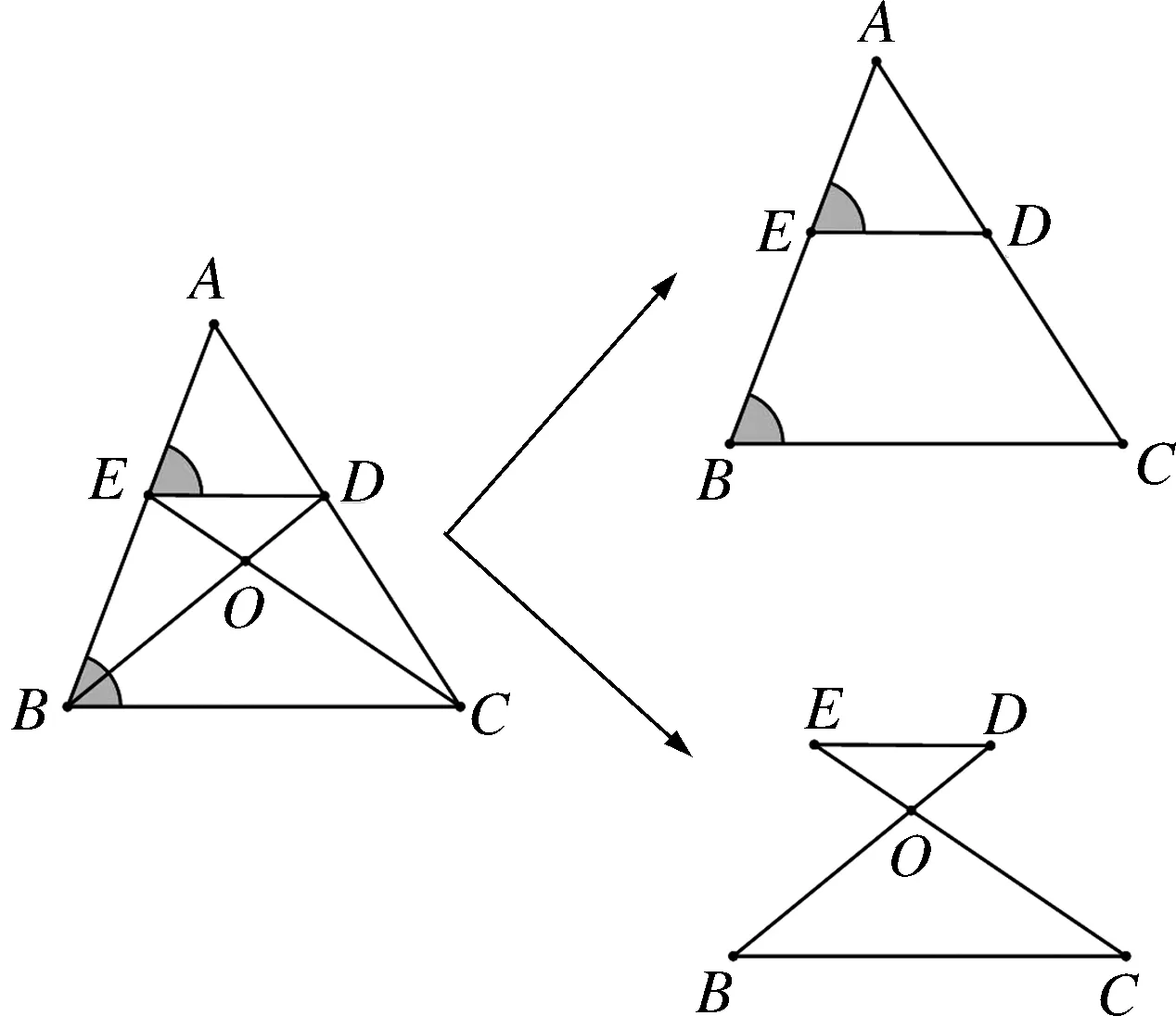
图6-1

图6-2
第3题中,当BD,CE都是△ABC的高时,除了一组斜A型图和一组蝶型图相似,另外还有4个直角三角形两两相似,共有8对相似三角形(分解图如图6-3所示).在学生经历思考后,可以让得分在3-6分的5位学生完成第3题,如有困难,可以让得分在9-12分的学生补充.最后教师展示出分解图,培养学生在复杂的几何图形中分离出基本图形的能力,从而提高学生分析问题的能力,找出其中的规律.
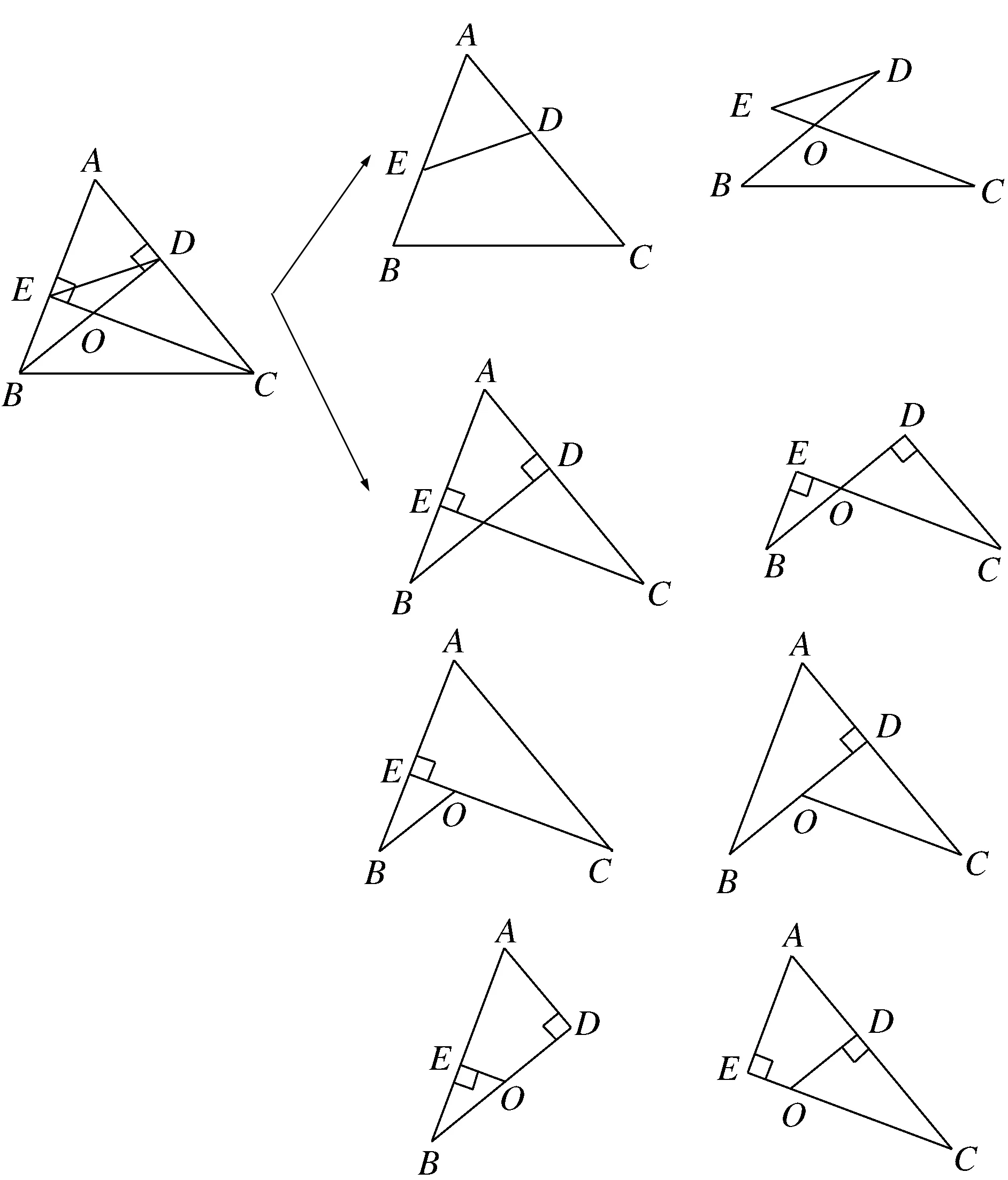
图6-3
四、精准评价,及时反馈,将课堂教学导向深度学习
一堂课是否成功关键要看学生在课堂上是否处于中心地位,学生的个性与能力是否得到充分发挥.许多传统的优质课堂像是在演戏,课堂活跃的气氛只体现在表面或形式上,并没有真正调动学生的积极性,多数学生并没有进入深层次的学习状态.只选择优秀学生解决简单问题的情况下,教师给予课堂的评价是片面、不客观的.运用极课数据辅助教学可以完善教学活动,客观评价学生的学习成果,有效反馈并及时调整,在教学过程中及时介入,精确指导.教学更加注重学生的发展,注重差异,学习变得更加私人订制化,最终达到发展学优生、提高中等生、帮助学困生的目的.由极课数据所提供的信息(如图7-1、图7-2所示)可清晰反映学生对基本图形的掌握情况.有5位学生只会证明简单的斜A型图,在课堂教学过程中就可以对这5位学生提问,弄清学生是否进行了有价值的思考,进入深度学习,从而给出合理评价,课后再对整个教学给出恰当的评价.
图7-1

图7-2
为培养学生的数学思维品质,引导学生进入深度学习,教师设计活动3.
活动3利用基本图形解决问题
题4如图8-1,在△ABC中,BD,CE是边AC,AB上的高,联结DE,已知△ADE面积与四边形BCDE面积相等,求∠A的度数.
图8-1
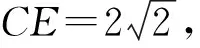
题6如图8-3,在△ABC中,P为边AB上的一点,M为CP的中点,AC=2.
(1)若∠PBM=∠ACP,AB=3,求BP的长;
(2)若∠ABC=45°,∠A=∠BMP=60°,求BP的长.

图8-2图8-3
设计说明:处理第4题时可以针对学困生设计如下问题链,引导学生找到AD与AB的比值.
问题1图中有哪些相似的三角形?
问题2由条件△ADE与四边形DEBC面积相等,能否得到S△ADE∶S△ABC的比值?
问题3∠A放在哪个直角三角形中较好?能否求出其三角比?
在大数据的背景下,以问题链为导向设计教学活动,兼顾学生的差异化需求,通过精准的提问激发学生学习兴趣,激励不同层次的学生,从而激发学生不停探索未知,保持对课堂的好奇心,让不同水平层次的学生都能从课堂上获得最大收益.第5题图形仍然是斜A型,渗透了函数解析式,解决过程还需要添加辅助线.训练针对中考综合题,思维容量更大,也为班级中学优生提供了增长空间.

通过一题多解调动学生学习的积极性,锻炼学生思维的灵活性与流畅性,培养学生的创新思维.
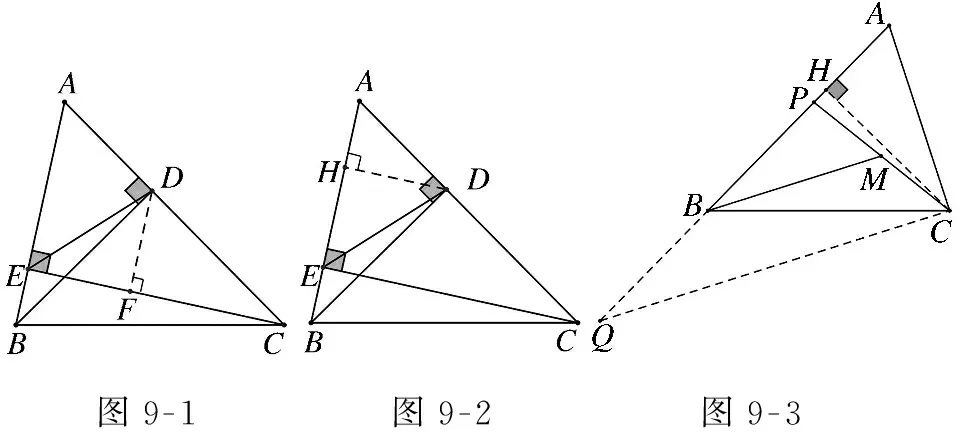
图9-1图9-2图9-3
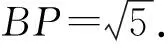
数据显示,班级中多数学生能掌握斜A型图的基本应用,所以有必要通过第5题、第6题的操练对这部分学生进行能力提升,将提优工作渗透到课堂教学中.在教学过程中,针对不同层次的学生的课堂表现,可以得出更精准的评价.对于解决了有难度问题的学优生,和解决了中低等难度的基础薄弱学生,都应该给予肯定的评价.从全体学生的思维表现得到的教学评价更胜于凭印象、凭感觉得出的评价.在随后的检测中,类似问题得分率上升至96%(如图10所示),说明经过本节复习课的深度学习,学生对相似基本图形的认识有进一步提高,分析、解决问题的能力得到了提升.

图10
随着教学技术的不断进步,大数据与精准教学深度融合,克服了精准教学在传统教学环境下操作的困难,为精准教学的应用提供了强有力的支持.运用极课数据进行精准教学可以改变传统教学的盲目性,进一步提升课堂教学的效率和水平.但目前限于技术条件,这种教学方式难以普及.随着教育理念的转变和教师素养的提高,相信未来这些现代化的教学方法一定会被更多人接受.教师可以充分利用大数据的技术优势,在教学中不断探索,不断提升技术水平和数据处理分析能力,为学生提供更加便捷、优质、有针对性的教学,从而全面实现课堂教学效果的综合提升.

