横观各向同性层合板理论编程实现与验证

陈州， 杜新喜， 张慎， 袁焕鑫

(1.中南建筑设计院股份有限公司， 武汉 430071； 2. 武汉大学土木建筑工程学院， 武汉 430072)

作为重要的结构形式之一，板式构件在几何上的显著特点是其中一个方向(厚度)的尺寸远小于其他两个方向(长度和宽度)。根据其组成材料成分的不同，它可以由同质或异质材料构成，例如将多层单层板黏合在一起组成整体的结构板(即层合板)。通常，单层板的性能与其材料及材料主轴有关。而层合板的材料力学性能，不仅取决于组成层合板的各层单层板的性能，有时还与各层单层板的铺设方式有关。作为一种复合材料，层合板具备单层板所没有的材料特点，为满足实际生活中不同的应用需求，工程上普遍使用层合板的结构形式。

其中，刨花板就是一种典型的复合材料板式构件，是将木材或非木材植物纤维原料加工成刨花(或碎料)，施加胶黏剂(和其他添加剂)，组坯成型并经热压而成的一类人造板材[1]。根据其结构不同，分为单层结构刨花板、三层(包括多层)结构刨花板、渐变结构刨花板、定向刨花板、华夫刨花板、模压刨花板等多种形式。随着中国对先进生产线的引进与升级，以及生产工艺的显著提高，近年来国内市场对刨花板的需求量不断增加，刨花板在建筑、家居、装饰装修等领域广泛使用。

板因其特殊的几何特点，通常对板式结构的分析不采用三维有限元。随着有限元方法的飞速发展，如何构造合乎要求的板单元这一中心问题，一直吸引着许多科研工作者。早在20世纪50年代末，便逐渐开展了针对板弯曲单元的研究，大致确定了两大类板理论有限元：基于Kirchhoff假设的薄板理论和Mindlin-Reissner中厚板理论[2]。由于薄板中要保持单元交界面上转角的连续(C1连续性)，使得薄板单元的构造相对困难；而基于厚板理论建立的单元，由于“剪切闭锁”现象的存在，只对中厚板有效，当板非常薄时，求得的位移趋于零。近几十年来，大量板单元相继被学者们提出并被构造。其中，值得一提的是基于离散Kirchhoff理论构造的离散Kirchhoff三角形(discrete Kirchhoff triangle，DKT)和离散Kirchhoff四边形(discrete Kirchhoff quadrilateral，DKQ)薄板弯曲单元[3-4]，及适用于中厚板的离散剪切三角形(discrete shear triangle，DST)单元和离散剪切四边形(discrete shear quadrangle，DSQ)单元[5]。这些单元被分别用于计算薄板及中厚板结构时都显示出良好的性能，在实际工程应用中具有较高的精度。

现基于复合材料宏观力学[6]分析方法，对三层结构刨花板进行结构静力试验及有限元数值分析。由于刨花板内部为交叉错落结构的颗粒状材料，结构均匀，在板平面内各方向材料特征基本相同，而垂直此面方向的性质不同，故采用横观各向同性[7-8]本构关系对刨花板的力学性能进行模拟。同时，对基于Kirchhoff薄板理论的DKT、DKQ薄板单元及基于Mindlin-Reissner中厚板理论的DST、DSQ中厚板单元进行有限元编程及性能验证，并介绍板构件、材料参数及节点位移转角在空间内全局坐标系中的转换方法。最后对比应用不同板单元时，对有限元模型计算的影响。

1 板理论及板有限元编程

1.1 横观各向同性板理论

板由于在几何上厚度尺寸远小于其他两个方向，故简化为二维问题可以减少计算工作量。如图1所示，板中面为平面Oxy，不可变形的线段Mm初始时垂直于板中面于点m。在板变形过程中，Mm保持笔直却不一定始终与中面垂直，即线段Mm为刚体运动。点m处的位移矢量记为u(m)，被定义为：u(m)=u(x,y)x+v(x,y)y+w(x,y)z。线段Mm绕x轴、y轴转角分别记为-βy、βx，即转角矢量θ=(-βy,βx, 0)。如图2所示，则M点处位移矢量可表示为

h为厚度；Lx为长度；Ly为宽度；L为垂直于各向同性面(T平面)方向

图2 板内任意线段Mm的运动学分析

u(M)=u(m)+Mm×θ

(1)

通常将板厚方向标记为1或z，故采用如下的标注方式为

(x,y,z)=(2,3,1)

(2)

板内任意一点M(x,y,z)的位移场u(M)由式(2)所定义。可见，板内位移场u(M)在板平面内的两个位移分量随纵坐标z(在板厚度上)线性变化，而横向位移(挠度w)仅为x和y的函数。由几何方程可得板内应变张量为

(3)

由式(3)可见，法向应变εzz=0，此为板理论中的基本假设。将各应变分量采用如下矢量形式表示为

(4)

1.1.1 横观各向同性板本构关系

对于横观各向同性材料，当各向同性面为xy面(z轴为旋转对称轴)时，其本构关系[9]表示为

(5)

通常，由于板的几何特征，法向应力与其他应力分量相比为可忽略的极小量σzz≈0，这也是板理论中常用的基本假设，将εzz=σzz=0代入式(5)得

(6)

故对于横观各向同性板式构件，当板平面xy为各向同性面(厚度为垂直于该面的方向z)时，其本构方程由式(6)给出，以矩阵形式表示为

(7)

式(7)中的本构矩阵记为C。类比式(4)中对应变的拆分方式，将应力及本构矩阵分为如下两部分。

(8)

板平面外应力-应变关系τ=C2γ，即

(9)

1.1.2 板内应变能及广义内力

节点位移在板中引起的应变能ED表示为

(10)

式(10)中：Ω为整个积分区域；S为板中面面积。

(11)

(12)

(13)

(14)

图3～图5描述了板横截面上的应力，这些应力与板平面内单位长度的力和力矩相联系，即广义内力。其中薄膜应力对应于式 (15)所示广义拉伸-压缩(Nxx,Nyy)及板平面内剪切(Nxy)力(图3)，表达式为

图3 广义拉伸-压缩及板平面内剪切力

(15)

广义横向剪力Q定义为横向剪切应力在板厚度方向的积分(图4)，表达式为

图4 广义横向剪力

(16)

弯曲及扭转应力与沿板边界上的广义弯矩(Mxx和Myy)及扭矩(Mxy)相联系(图5)，表达式为

图5 广义弯(扭)矩

(17)

在x、y方向上，板的力矩平衡方程[10]为

(18)

1.1.3 横向剪切的影响

Kirchhoff薄板理论类比于经典梁理论(欧拉-伯努利梁理论)，忽略了横向剪切变形的影响，假设横向剪切应变γxz及γyz为0，即

(19)

式(19)表征了薄板中挠度w与转角矢量θ间的运动学关系：初始状态下垂直于板中面的法线在变形过程中(及变形后)始终垂直于中面。Kirchhoff模型主要适用于沿厚度方向分布均匀的薄板(h/L≤1/10，L代表板的长度及宽度)。

Mindlin-Reissner中厚板理论类比于铁木辛柯梁理论，考虑了横向剪切应变γxz及γyz，并与广义横向剪力Q相联系[式(16)]。如同铁木辛柯梁的情况，考虑到实际的剪切应变沿板厚度方向并非均匀分布，基于三维弹性理论剪切应变能等效原则，引入校正系数k=5/6代入式(16)，则Mindlin-Reissner中厚板内，广义横向剪力与横向剪切应变的关系定义为

(20)

中厚板在变形过程中，初始状态下垂直于板中面的法线不再要求始终垂直于中面。Mindlin-Reissner模型适合于当板的组成成分为不均匀、各向异性材料，及层合板的建模。事实上，在这些类型板结构中横向剪切作用占据重要因素，不可忽略。

1.2 DKT,DKQ,DST,DSQ板有限单元编程

基于平板弯曲问题的特殊性，自有限元方法发展伊始，大量工作投入到了构造板(及壳)单元的研究之中[11]。近60年来，板壳有限元分析一直是研究的热点，有关板壳有限元的研究文献已数以千计，文献[12]引用了约150个板的有限元列示。仅对基于离散Kirchhoff理论构造的三角形单元(DKT)和四边形单元(DKQ，适用于薄板)及包含横向剪切作用(无剪切锁闭)的三角形单元(DST)和四边形单元(DSQ，适用于中厚板)的构造过程做清晰详细的介绍与梳理。这些单元间的共同点在于基于单元应变能构造单元刚度矩阵，即

(21)

参考式 (11)～式 (14)中对整个板内应变能的定义如下。

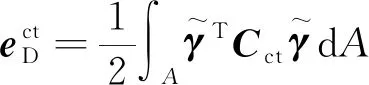
1.2.1 单元位移场插值

若对位移场各分量进行经典离散，采用等参单元分别独立插值，即

(22)

将导致剪切锁闭现象，即当板厚趋于零时，中厚板理论并没有退化为薄板理论，剪切变形没有趋于零。这是因为当板较厚时，扰度w及转角βx、βy为独立变量，而当板非常薄时，βx、βy为w的导数[见式(19)],而非独立变量。

板单元DKT、DKQ、DST、DSQ对位移场各分量采用了如下的插值函数[3-5,13]。

(23)

式(23)中：n为单元节点数，对DKT、DST 单元，n=3，对DKQ、DSQ单元，n=4。如图6所示，以三角形单元为例，n、s分别为垂直及沿边ij的单位向量，对ij边上的任意一点k分别定义切向转角βs及法向转角βn为

图6 切向转角βs及法向转角βn

(24)

式(24)中：Ck=(xj-xi)/Lk；Sk=(yj-yi)/Lk，

表1 单元DKT、DST、DKQ、DSQ的形函数

图7 基准单元节点及边编号

在各边界上，切向转角βs二次变化，法向转角βn线性变化(图8)，它们由角节点上的参数完全确定，表达式为

图8 转角沿坐标在边上的变化

(25)

式(25)中：s′=s/Lk∈[0,1]；αk为变量，与切向转角βs相关联。

物理坐标系(x,y)与基准坐标系(ξ,η)之间的等参变换公式为

(26)

并采用表1中的插值函数Ni(ξ,η)。两种坐标系间偏导数映射关系由雅可比矩阵J相联系，即

(27)

式(27)中：J中各元素Jij表达式见表2，其逆矩阵记为j=J-1。

表2 雅可比矩阵J中各元素Jij表达式

1.2.2 单元应变场插值

单元薄膜应变场分量表示如下。

(28)

以矩阵形式表示为

(29)

式(29)中：Bm为薄膜应变几何函数矩阵；Um为板平面内位移场矢量；Bm及Um定义如下。

(30)

单元曲率(及扭率)场χ和横向剪切应变场γ的插值过程相对单元薄膜应变场e复杂。对于DKT和DKQ单元，变量αk可以通过横向剪切应变为0(Kirchhoff薄板假设)导出，即

(31)

将式(24)代入式(31)积分得

Ckβxj+Skβyj)

(32)

转角βx、βy的插值函数由式(23)给出，可得

(33)

式(33)中：

(34)

式(34)中：Uf为挠度转角矢量；指标k、m被定义为以节点顶点i为公共点的两边(见图7)，其编号取值见表3；插值函数Ni、Pk表达式见表1。

表3 DKT, DKQ单元节点及边编号i、k、m

DKT、DKQ单元曲率(及扭率)场χ为

(35)

(36)

对于DST及DSQ单元，由于需要考虑横向剪切应变，式(31)～式(32)不再适用。DST、DSQ单元曲率(及扭率)场χ为

χ=BfβUf+Bfαα

(37)

式(37)中：

(38)

且单元横向剪切应变能为

(39)

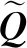
(40)

式(40)中：

(41)

Cfij(i,j=1,…,3)为矩阵Cf[式(13)]中的元素，βx及βy采用式(23)所示的方式插值得

βxx=PfUf+T2Tαα

(42)

式(42)中：

(43)

(44)

(45)

联立式(40)及式(42)可得

(46)

(47)

类比式 (31)，式(47)积分为

(48)

式(48)以矩阵形式表示为

(49)

式(49)中：Aα、Aw表达式如式(50)、式(51)所示。

(52)

(50)

(51)

(53)

1.2.3 单元刚度矩阵

(54)

(55)

对于DST、DSQ单元，考虑了横向剪切的影响，故单元应变能eD为

(56)

其中单元薄膜刚度矩阵Km见式(55)，且

(57)

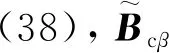
(58)

并将式(49)与式(58)代入式(56)，得DST、DSQ单元应变能eD为

(59)

式(59)中：

(60)

根据式(54)与式(59)，对于DKT、DKQ、DST、DSQ板单元，单元应变能eD统一表示为

(61)

式(61)中：U2d=[u1v1w1βx1βy1…unvnwnβxnβyn]T为单元节点位移矢量，每个节点5个自由度；K2d为板单元刚度矩阵。

2 层合板结构静力试验及数值分析

2.1 横观各向同性板结构静力试验

如图9所示，试验样品为由刨花板组装而成的办公桌。试验开始之前将各板拧紧拼装，并储存在相对湿度50%±5%及室温(23±2) ℃的环境中。试验在温度范围介于15～25 ℃的环境条件下进行。试验荷载通过负载垫施加于桌面中心，负载垫对应于图9的直径为80 mm，具有光滑、平坦接触表面的刚性圆柱体。在所施加荷载点的对立面设置LVDT位移传感器并与书桌下表面相接触，以测量相对应的荷载点处的位移值。测试过程中，分批次分别施加3级荷载F为300、400、500 N，每次均缓慢施加力以忽略动态影响，且每次所施加的静态力均保持10 s以记录实验数据(力和位移)。为了减少试验测量的不确定性因素，每级荷载施加10次，并计算得出测量的平均值以代表该级荷载-位移的试验结果。板中心扰度定义为在没有施加力时的初始状态和施加荷载后的最终状态之间位移计读书的差值。每级荷载下位移计的初始及最终读数统计于表4。

图9 垂直静力荷载试验

表4 每级荷载作用下位移计初始及最终读数

2.2 DKT,DKQ,DST,DSQ板单元验证及性能比较

关于厚薄板弯曲问题的理论解，有大量文献涵盖了基于Kirchhoff薄板及Mindlin-Reissner中厚板理论的矩形及圆形板在不同荷载及边界条件下的理论解[14-15]。其中，对于边界简支或固定的矩形板，其理论解通常采用级数法或伽辽金方法的近似解法，而无精确解。比较了圆板分别在中心点荷载及板平面均布荷载作用下、边界简支及固定时，圆心挠度的理论精确解与有限元数值解，从而验证前述4种板单元的性能。

如图10所示的圆板，其直径为R，厚度h≪R，由均质各向同性线弹性材料制成，其弹性模量为E，剪切模量为G，泊松比为ν，抗弯刚度D=Eh3/[12(1-ν2)]。

图10 圆板受均布荷载

此为轴对称问题，以圆心为原点，建立圆柱坐标系(er,eθ,ez)，板内某点的横向位移(挠度)w(r)及转角θθ(r)均仅为径向距离r的函数。对于物理量s(s表示挠度w或转角θθ)，定义s的理论解sana与有限元数值解snum之间的相对误差函数Errors为

(62)

式(62)中：=·=为L2范数。

当荷载及边界条件不同时，基于两种板理论求得的挠度及转角的理论解分别归纳如下。

(1)板边界固定、板面受均布荷载p。

(63)

(2)板边界简支、板面受均布荷载p。

(64)

(3)板边界固定、中心受集中荷载P。

(65)

(4)板边界简支、中心受集中荷载P。

(66)

DKT、DKQ、DST、DSQ板单元性能的评估可通过计算板在不同边界条件下，挠度及转角的解析解和有限元数值解间的相对误差而实现。图11～图14展示了圆形板分别在边界固定、简支、板面受均布荷载、圆心受集中荷载作用时，对应不同的板单元，在除圆心以外所有节点的相对误差[式(62)]随板单元数量的变化规律。各个板单元的有限元数值解通过MATLAB软件计算。

图11 挠度及转角相对误差随单元数量的演变(板边固定、板面受均布荷载)

图12 挠度及转角相对误差随单元数量的演变(板边简支、板面受均布荷载)

图13 挠度及转角相对误差随单元数量的演变(板边固定、中心受集中荷载)

图14 挠度及转角相对误差随单元数量的演变(板边简支、中心受集中荷载)

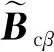
2.3 板在空间内的组装与坐标变换

图9所示的办公桌为板式构件组成的空间结构。如图15所示，以三节点三角形单元为例，解释说明板在空间的组装。该三角形单元位于由全局(或空间)坐标系(X,Y,Z)组成的空间体系中。对于每个单元定义局部坐标系(x,y,z)。

图15 空间内三节点三角形板单元

则矢量y定义为：y=z×x。

在全局坐标系(X,Y,Z)及局部坐标系(x,y,z)中，节点i的位移ui及转角Ωi分别定义如下。

(67)

可得单元节点上5个自由度表示为

(68)

引入矩阵T，式(68)以矩阵形式表示为

(69)

式(69)中：大小为5n×6n矩阵T对应于位移场从全局坐标系到局部坐标系的转换矩阵，式(61)中单元应变能为

(70)

式(70)中：K2d为板平面内单元刚度矩阵。在空间内，单元刚度矩阵定义为

K3d=TTK2dT

(71)

同理，2.1节中介绍的代表材料弹性特征的本构关系也必须由局部坐标系转换为在空间的全局坐标系中表示，以实现单元刚度矩阵的组装。为此，定义局部坐标系(x,y,z)与空间坐标系(X,Y,Z)间的过渡矩阵P为

(72)

矩阵P为正交矩阵(P-1=PT)，P的列分别对应于矢量X、Y、Z的坐标在局部坐标系(x,y,z)中的表达式。

应力及应变张量分量在全局坐标系(X,Y,Z)中分别表示为σ′ij及ε′ij，与其局部坐标系中分量σij及εij间的转换定律为

(73)

式(73)中：下标i,j,k,l=1,2,3。

广义胡克定律在局部坐标系(x,y,z)中表示为

(74)

式(74)中：Cijkl及Sijkl分别为四阶刚度张量C及柔度张量S在局部坐标系中分量。将式(74)所示的广义胡克定律在全局坐标系(X,Y,Z)中表示，可得Cijkl与四阶刚度张量C′在全局坐标系(X,Y,Z)中分量C′ijkl之间的转换关系为

(75)

式(75)中：下标i,j,k,l=1,2,3;p,q,r,s=1,2,3。

对四阶柔度张量S及S′在局部坐标系与全局坐标系中的分量Sijkl与S′ijkl间的转换关系可采用与式(75)相似的方式。

利用Voigt标记，对下标设置如下转换规则，即

11↔1, 22↔2, 33↔3, 23或32↔4， 13或31↔5， 12或21↔6

(76)

可将应力、应变张量表示成向量形式为

(77)

及将四阶刚度张量C(或C′)及柔度张量S(或S′)表示成6×6矩阵C(或C′)及S(或S′)为

(78)

可得矢量形式的应力、应变及二阶6×6矩阵形式的刚度张量及柔度张量分别在局部坐标系与全局坐标系中的转换关系如下。

(79)

式(79)中：Mσ及Mε为大小6×6的可逆矩阵，具有如下形式。

(80)

式(80)中：子矩阵A、B、D1、D2为

(81)

易得矩阵Mσ与Mε间联系为

(82)

矩阵Mσ与Mε不同的主要原因在于式(77)中定义应力、应变矢量时，切应变分量中系数2的存在，而切应力分量没有。

2.4 有限元数值分析

图16展示了通过MATLAB软件，将各个板构件组装成图9所示的试验办公桌模型，实际的三维板式构件由板中面表示。

各板编号1、2、3的尺寸见表5。在办公桌中心处通过直径D=80 mm的圆柱形负载垫施加的集中力荷载F，由板中心直径为D的圆上均布荷载p=4F/(πD2)表示。不考虑书桌与地面间的相对滑动(事实上试验过程中也未见)，故在桌脚处采用固定的边界条件。

表5 板构件尺寸

刨花板材料的力学性能由“横观各向同性”本构关系模拟。由式(7)可见，影响横观各向同性板式构件的材料参数仅有3个：横向弹性模量ET，横向泊松比νT及纵向剪切模量GL。对刨花板材料参数的测量[8-9]并非重点内容。事先采用文献[16]方法对刨花板各项力学参数进行了试验测量，结果统计见表6。

表6 刨花板材料参数测量结果平均值

分别应用Kirchhoff薄板单元(DKT、DKQ单元)及Mindlin-Reissner中厚板单元(DST单元)代入有限元模型计算桌面中心点处挠度，并与3.1节中试验测量值相比较，结果见表7。图16对应于施加中心集中荷载F=300 N、并采用DKT单元计算时，在全局坐标系下竖向位移云图。由表7统计结果可见，薄板与中厚板有限元单元计算结果均能满足工程计算精度，但对于计算刨花板这种夹层材料复合板，考虑剪切作用的中厚板单元比薄板单元计算更加精确。

图16 板结构静力试验模拟

表7 试验测量值与有限元数值解比较

3 结论

随着有限元方法的发展，对板(及壳)有限元的研究，如何构造出经济、高效、厚薄板通用的板有限单元，一直吸引着众多科研工作者的目光。以刨花板材料板式结构办公桌家具为例，对其进行了静力荷载试验及有限元数值分析，并进行了结果对比，得到主要结论及展望如下。

以刨花板代表的层合板，因其特殊的物理构造，在各向同性平面内材料的力学性质大致相同，而垂直于此方向不同，故可以采用横观各向同性本构关系对其建模。影响横观各向同性材料的弹性参数有5个：纵向、横向弹性模量EL、ET，纵向、横向泊松比νL、νT及纵向剪切模量GL。板式构件由于在厚度方向尺寸远小于其他两个方向，其法向正应力通常被忽略不计。将这一假设代入横观各向同性材料本构方程，得到了横观各向同性板式构件的本构关系。影响横观各向同性板的力学参数仅有3个：ET、νT及GL。

基于薄板及中厚板理论中对横向剪切不同的假设，对DKT、DKQ薄板单元及DST、DSQ中厚板单元的构造方法进行了详细的梳理与介绍。通过对比圆板弯曲问题中理论解的精确值与有限元数值解的相对误差，对各个板单元的性能进行了验证。结果表明，DKT、DKQ及DST单元是足够精确可靠的，造成DSQ单元数值解不收敛于理论解的主要原因，分析认为主要在于对横向剪力插值的几何函数矩阵中，高斯近似积分法的应用。同时介绍了板构件在空间内的组装及材料参数、节点自由度分量向空间全局坐标系的转换方法。

将刨花板材料参数的测量平均值及DKT、DKQ、DST单元分别代入有限元模型进行计算，并与板结构静力试验结果对比，可见上述板单元均能满足工程精度，而考虑横向剪切作用的DST中厚板单元对层合板的计算结果更加精确。仅从不同的板单元及材料参数的平均值，对有限元模型进行了计算，其结果具有一定的偶然性。事实上，影响该有限元模型的因素除此之外主要还有刨花板材料参数的离散性，及各板式构件之间的连接刚度等。

为此，展望如下：①构造刨花板材料参数随机概率模型；②试验测量板式构件之间连接件的实际刚度，并代入有限元模型计算。