两角差余弦公式引入方式的比较研究*

215300 昆山文峰高级中学 李兆强

221000 江苏省徐州市第一中学 丁永刚

1 研究背景

任何数学公式都有其产生的背景，只有让学生在课堂上经历公式的发现过程，这样的教学才是自然的、朴实的.两角差余弦公式脱胎于平面几何，与余弦定理、射影定理等三角学的重要定理、公式以及复数知识都有密切的联系.研究两角差余弦公式有助于培养学生数学运算、逻辑推理、直观想象、数学建模等素养.《普通高中数学课程标准(2017年版)》(以下简称“课标”)要求：“知道两角差余弦公式的意义、经历公式的产生过程，能从余弦推导正弦、正切.”因此，研究两角差余弦公式如何引入很有必要.

如表1所示，在呈现方式上，人教版教材从现实情境出发，沪教版和苏教版教材从数学情境出发引入公式.人教版教材利用几何方法和向量方法证明公式，沪教版教材利用单位圆中两点距离公式证明，苏教版教材用向量方法证明.在前后知识顺序上，三个版本教材差别不大，都是从余弦推导正弦、正切公式.

表1 三版教材中的“两角差的余弦公式”

2 理论基础

对于同一个数学公式，每位教师的引入方式是不一样的，即使教师使用同样的教学设计方案，课堂中出现的情况也是千差万别.学生对教学目标、教学内容、教学手段和教学方法的理解和解读也大相径庭.影响教学的心理学原理有以下两种.

2.1 班杜拉社会学习论

美国心理学家班杜拉通过实验得出了著名的社会认知论，他认为，教师有什么样的课堂教学价值观，以及是否及时巧妙地对学生的各种表现或表达予以强化，决定了学生课堂的行为状态，也决定了课堂是否有利于教学生成.因此，好的课堂需要教师提前做出好的教学设计.

2.2 建构主义学习论

以皮亚杰为代表人物的建构主义学习论认为，知识不是通过教师传授获得的，而是学习者在一定的情境下，通过意义建构获得的.建构主义教学设计遵循下列原则：(1)问题驱动学习；(2)真实情境展开；(3)任务提供资源.因此，好的公式引入设计必须搭建学习的“脚手架”.

3 研究过程

公元2世纪，古希腊天文学家托勒密在编制弦表时，使用了包括两角差余弦公式在内的三角公式，这是有史可考的两角差余弦公式的最早记载.继托勒密之后，许多天文学家和数学家相继设计新的方法推导该公式，不断为两角差余弦公式的历史增添新的篇章，他们的研究方法大都比较复杂.笔者结合多年的研究实践，以苏教版教材为例，梳理六种不同的两角差余弦公式引入方式，并加以比较.

3.1 引入方式

方式1：生搬教材(新手型教师)

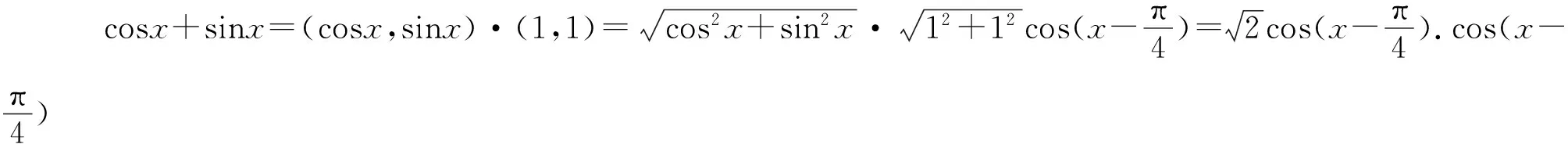
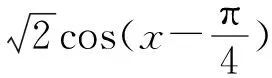
方式2：旧知引入(经验型教师)

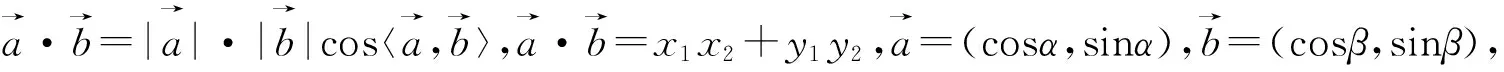
分析：由向量的数量积的两种不同计算公式这一旧知引入新知，直截了当，问题铺垫，单刀直入，一步到位得出公式，复习了数量积的计算公式，但过程过于简单，缺乏探究的乐趣，在理解学生、理解教学、理解数学上都存在欠缺，不利于学生的学和教师的教.

方式3：改进教材(成熟型教师)

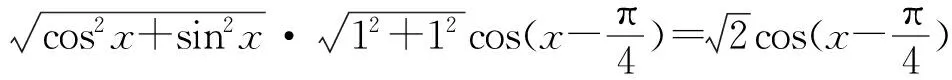
生：在单位圆x2+y2=1上.

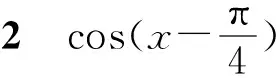
生：单位圆上旋转角.

问题3cos(α-β)中α，β分别对应哪两个点的旋转角？

生：(cosα,sinα)和(cosβ,sinβ).

问题4在向量的哪个公式中会出现cos(α-β)？

问题5如何求cos(α-β)？

生：构造点(cosα,sinα)和(cosβ,sinβ)，利用数量积公式推导.

分析：设计五个问题组成问题串，引出单位圆，利用数量积推导两角差余弦公式，公式引入比较自然，问题设置十分巧妙，探究过程非常“隐蔽”.

方式4：实验探究(骨干型教师)

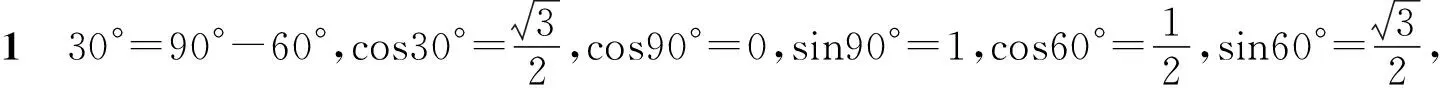
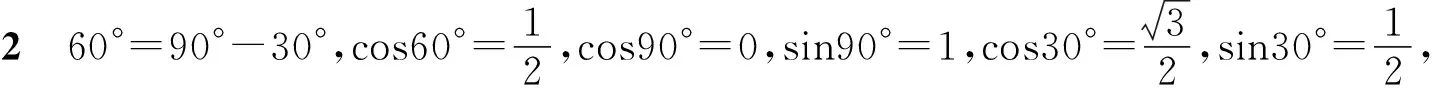
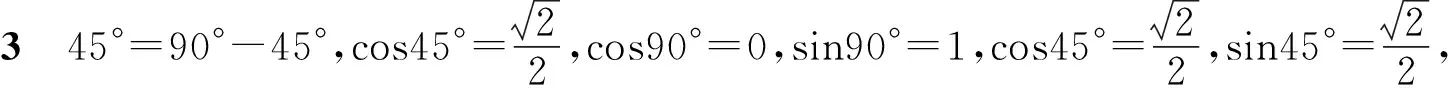
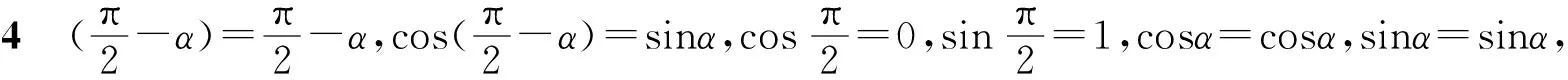
问题5你能发现cos(α-β)，cosα,cosβ,sinα,sinβ这五个式子的等量关系吗？

分析：由探究特殊角三角函数值间的关系入手，归纳任意两角差的余弦公式，但设置的问题有些突兀，教师的主观意志强，缺乏必要的引导，公式的发现成为“被发现”，课堂可能会出现新的生成.

方式5：几何模型(专家型教师)

问题1如图1、图2，如何借助下列图形证明勾股定理？

问题2如图3、图4，将直角三角形的斜边长改为1，其中的一个锐角改为θ，证明cos2θ+sin2θ=1.

问题3如图5、图6，两对斜边为1的直角三角形，一对含锐角α，一对含锐角β，探究有关α、β的等式.

分析：巧设问题，引导探究，从四个全等直角三角形到两组全等直角三角形，从一个锐角到两个锐角，学生感悟了数学问题的产生、发展的过程，积累了借助几何图形发现数学结论的活动经验，培养了几何直观素养，训练了类比推理.

方式6：单位圆模型(名家型教师)

问题托勒密定理告诉我们，圆的内接凸四边形中，两组对边乘积的和等于两条对角线的乘积，即AC·BD=AB·CD+AD·BC，如图7，设∠DAC=α,∠ACB=β，半径OA=1，你能得出什么结论？

分析：根据著名的托勒密定理设置开放性的问题，让学生自主探究，小组合作，探索未知的结论，这是课堂教学中的“真探究”.

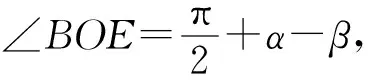
分析：学生通过托勒密定理推导两角差余弦公式，感受古人的数学智慧，了解数学史和数学文化，增强数学学习的热情和自信.

3.2 比较研究

受教师教学理念、学生学习能力差异等因素的制约，在苏教版教材编写意图的引导下，不同的教师会选择不同的公式引入方式.

3.2.1 研究引入方式，提升数学抽象素养

高中是学生数学抽象素养提升的关键阶段，然而，如何才能更高效地提升学生的数学抽象素养，依然存在很多不明确的因素.例如，方式1虽然取自教材，但由于缺少必要的“台阶”，学生的数学抽象素养很难得到提升.方式2虽然过程简洁，但只是做了一次等量代换，一次代入坐标运算，谈不上提升数学抽象素养.方式3中的五个问题形成问题串层层递进，引导学生探究，由浅入深提升了学生数学抽象能力.方式4从特殊到一般，方式5利用图形的拼凑，方式6利用公式的变形，贴近学生的能力基础与知识经验，使高中生在获得“四基”、提升“四能”的基础上，训练数学抽象思维，提升数学抽象素养.

3.2.2 列举具体实例，夯实先行组织策略

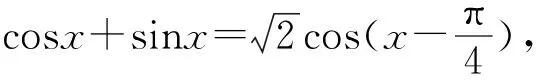
①设计自然原则 引入公式既要对学生充分了解，又要对教材进行合理的预设，既要承上又要启下，对此，方式3体现得尤为突出.

②循序渐进原则 不同的学生有不同的最近发展区，因此，引入公式时要考虑学生的均衡程度，循序渐进地设置问题，不可一蹴而就，如方式3、方式4的五个问题，方式5的三个问题都很好地遵循了这一原则.

③留有余地原则 引入公式时不能“面面俱到、无微不至”，不能“填满”学生的最近发展区，要适当给学生的思维空间“留白”.如方式5可以放手让学生自由拼凑，学生可以拼凑出“五花八门”的图形，给学生的思维留出充分的余地，有时会有意想不到的收获.

4 教后反思

课标提出把握数学本质，创设教学情境，感悟数学的科学价值、应用价值、文化价值和审美价值[1]，如何在公式引入课教学中落实“四基”，训练“四能”？笔者认为好的公式引入课要做到以下四点.

4.1 融入数学历史

引入方式5(几何模型)和引入方式6(单位圆模型)适当引入了数学史的元素，两则史料对应了“经历两角差余弦公式的推导过程”“培养直观想象素养”“激发数学学习兴趣”的教学目标，符合有效性原则，“两角差余弦公式的几何模型”史料与勾股定理的证明一脉相承，符合可学性原则.

4.2 过程设计须自然

历史上，两角差的余弦公式经历了从锐角到任意角情形，从几何方法到解析方法的演进过程，学生在初中学过勾股定理的证明，引入方式5从勾股定理证明到cos2θ+sin2θ=1的证明，再到两角差余弦公式的证明，中间过渡较为自然，教师在讲解证明方法时，学生进行类比推理较为轻松，这都源于公式证明过程设计的自然.

4.3 关注学科育人

六种教学设计，从锐角到任意角、从三角到几何、从猜想到证明，再现了两角差余弦公式发生、发展的过程，呈现了“知识之谐”.六种不同的呈现方式，六类不同教师(新手型、经验型、成熟型、骨干型、专家型、名家型)的引入方式，展示了“方法之美”.教师引导学生获得成功的体验，营造了“探究之乐”.数形结合法揭示了代数与几何的联系，培养了学生的直观想象素养，成就“能力之助”.引导学生了解数学史，小组合作互相启发，培养了倾听、尊重的品质，体现出“德育之效”[2].

4.4 培养实践思维

在开展两角差余弦公式教学时，很多教师更关注公式的实用性，对公式的产生过程重视不够.笔者列举的六种引入方式将知识的产生过程置于初高中庞大的知识体系中，紧扣几何图形设计实践活动，积极强化学生实践活动经验.在引入公式时，设计层层递进的问题，点燃思维的火花，引导深度思考、深度探究，使学生积累的经验逐步归一，完善学生思维体系，丰富学生思维活动经验[3].实践活动经验和思维活动经验紧密联系，只有二者同时培养、双管齐下，才能全面提升学生数学核心素养.