针对轻量级分组密码算法PRESENT的随机差分故障攻击

黄湘蜀, 王 敏, 杜之波, 吴 震, 王 燚

(成都信息工程大学网络空间安全学院,四川 成都 610225)

0 引言

轻量级分组密码算法凭借其结构简单、功耗低、实现面积小、适应性广泛等特点,已经成为物联网应用的关键组成部分。目前在物联网应用中,已经有许多轻量级分组密码算法,如 MIBS[1]、TWINE[2]、HIGHT[3]、GIFT[4]。这些算法都具有加解密一致、结构简单、易于实现等特点。而 PRESENT算法是 A.Bogdanov等[5]提出的一种轻量级分组密码算法,其具有轻量级分组密码普遍特点,同样适合在物联网相关应用中使用。当前针对PRESENT算法的分析方法主要有积分攻击[5]、差分代数攻击[6]、多重差分链攻击[7]以及差分故障攻击[8-9]等方法,文献[5]通过分析PRESENT算法一系列中间状态的和的概率进行攻击,攻击复杂度为220。文献[6]将差分攻击和代数攻击相结合,建立并且简化代数方程组,攻击复杂度为264.58。文献[7]利用多重差分链对PRESENT算法进行攻击,攻击复杂度为281。差分故障攻击[10]作为旁路攻击[11]的一种,最早在1996年由Boneh提出,是一种将差分分析[12]和故障攻击[13]相结合的技术。攻击原理是在加密过程中的某一时间段进行故障注入,制造数据差分,利用输出的故障密文和故障动作,结合差分方程得到轮密钥的可能值。该方法已经应用于 CLEFIA[14]、SM4[15]等分组密码上,对分组密码算法构成了严重的威胁。文献[8]采用的是面向字节的随机故障注入模型,在PRESENT算法的加密过程中引入单字节的故障,通过差分故障特性识别需要的故障密文,并由识别得到的故障密文恢复轮密钥。文献[9]建立单字节的随机故障模型,利用PRESENT算法P置换层的故障传播特性,通过单字节扩展的方式恢复轮子密钥,攻击复杂度为231。现有的两种方法虽然都在理论上进行了证实,但在实际操作中攻击者难以控制故障注入的位置以及产生故障的字节数,所以当前针对PRESENT算法的故障注入攻击仍然有一定的局限性。

针对上述问题,为提高故障攻击方法在实际攻击中的可行性以及效率,降低故障注入的难度,对现有的单字节差分故障模型进行改进,利用固定的故障传播路径,建立多字节的故障注入模型。通过电压注入的方式在第30、29轮任意位置进行随机故障注入,并由输出差分与S盒输入值之间的关系,筛选出正确的S盒输入。设计的故障模型,可将攻击复杂度降低41.9%,攻击平均时间由20000 ms降低到1000 ms。

1 PRESENT算法

1.1 符号说明

K:表示密钥;

ki:表示当前轮密钥的第i比特位;

p(i):第i比特位的置换运算;

S[]:表示S替换;

Si:表示第i轮S盒输入;

Pi:表示第i轮P盒输入;

Ci:表示第i轮P盒输出;

Nci:表示经过第i轮P置换后故障变化到的比特位置;

Nsi:表示第i轮故障所在的S盒;

f:表示输入差分;

f＇:表示输出差分;

Sin:S盒的输入值;

F(f＇):表示输出差分为f＇时,输入差分的候选集合。

1.2 PRESENT算法迭代过程

PRESENT算法的明文和密文长度都为64比特,主密钥长度为80比特或者128比特,文中仅讨论80比特的情况。该算法共有31轮迭代过程,每一轮的子密钥长度为64比特,如图1所示,在第31轮结束后,再进行一次轮密钥加的白化操作。

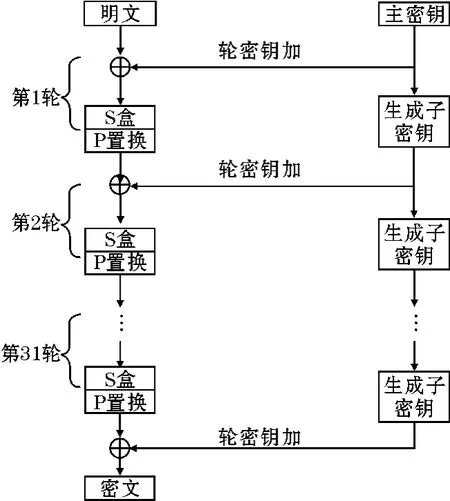
图1 PRESENT算法加密流程

算法主要是由 “轮密钥加”“S盒置换”“P盒置换”3部分组成。“轮密钥加”为按位进行异或操作。“S盒置换”为按照S盒置换表进行置换,每个S盒输入和输出都是4比特(为方便阐述,文中将4bits视作一个字节),由16个S盒组成,一共64比特,S盒置换如表1所示。

表1 S盒置换表

“P盒置换”相当于移位操作,每比特位置按式(1)进行置换,其中i为比特位。

1.3 PRESENT密钥扩展

以80比特的主密钥为例来阐述PRESENT算法的密钥扩展方法。主密钥首先存储在存储器中,表示为K=k79k78…k0,在进行轮密钥加操作时按位取当前密钥寄存器的高64比特,表示为K=k79k78…k17k16。提取完子密钥后按如下方式进行扩展。首先,将80比特密钥循环左移61位,之后依次从左到右取4比特进行S盒置换,最后将k19k18k17k16k15与轮计数器r做异或运算,并且将异或后产生的结果取代原来的5比特数据,如式(2)所示。

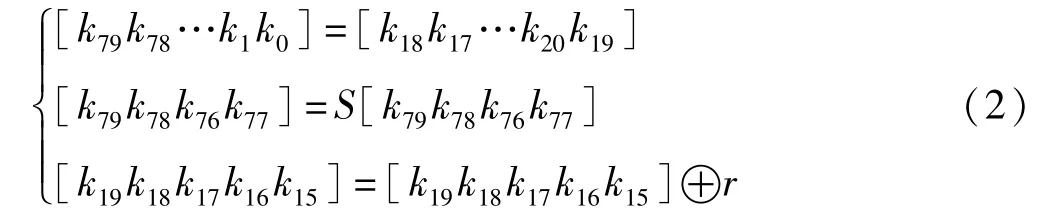
2 PRESENT分组密码故障分析

2.1 PRESENT算法故障传播路径

PRESENT算法属于轻量级分组密码算法的一种,算法中的S盒和P置换是重要的组成成分,在故障攻击中攻击者可以根据S盒的非线性将S盒的输入缩小范围,通过对P置换的分析得到故障的传播路径。图2是最后两轮加密过程。

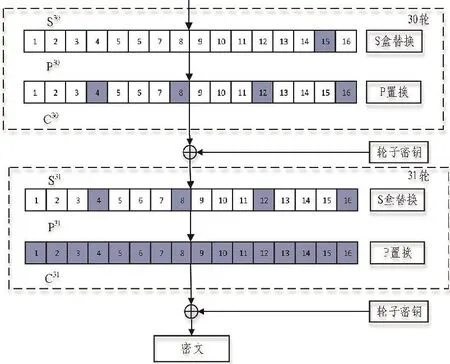
图2 PRESENT算法最后两轮加密过程

图2中,首先以单字节故障进行说明,多字节故障传播类似。假设在S30第15个字节处产生了单字节的故障,由于一个字节表示4bits,即最多4比特位的数据产生了变化。此时经过P置换后,该故障数据会传播到S31的4个不同的S盒上,这4个S盒都会受到故障数据的影响。若再经过一次P置换运算,那么所有字节都会受到故障数据的影响。表2是故障传播路径表,其中i(0≤i≤15)表示在第30轮注入单字节故障的位置。

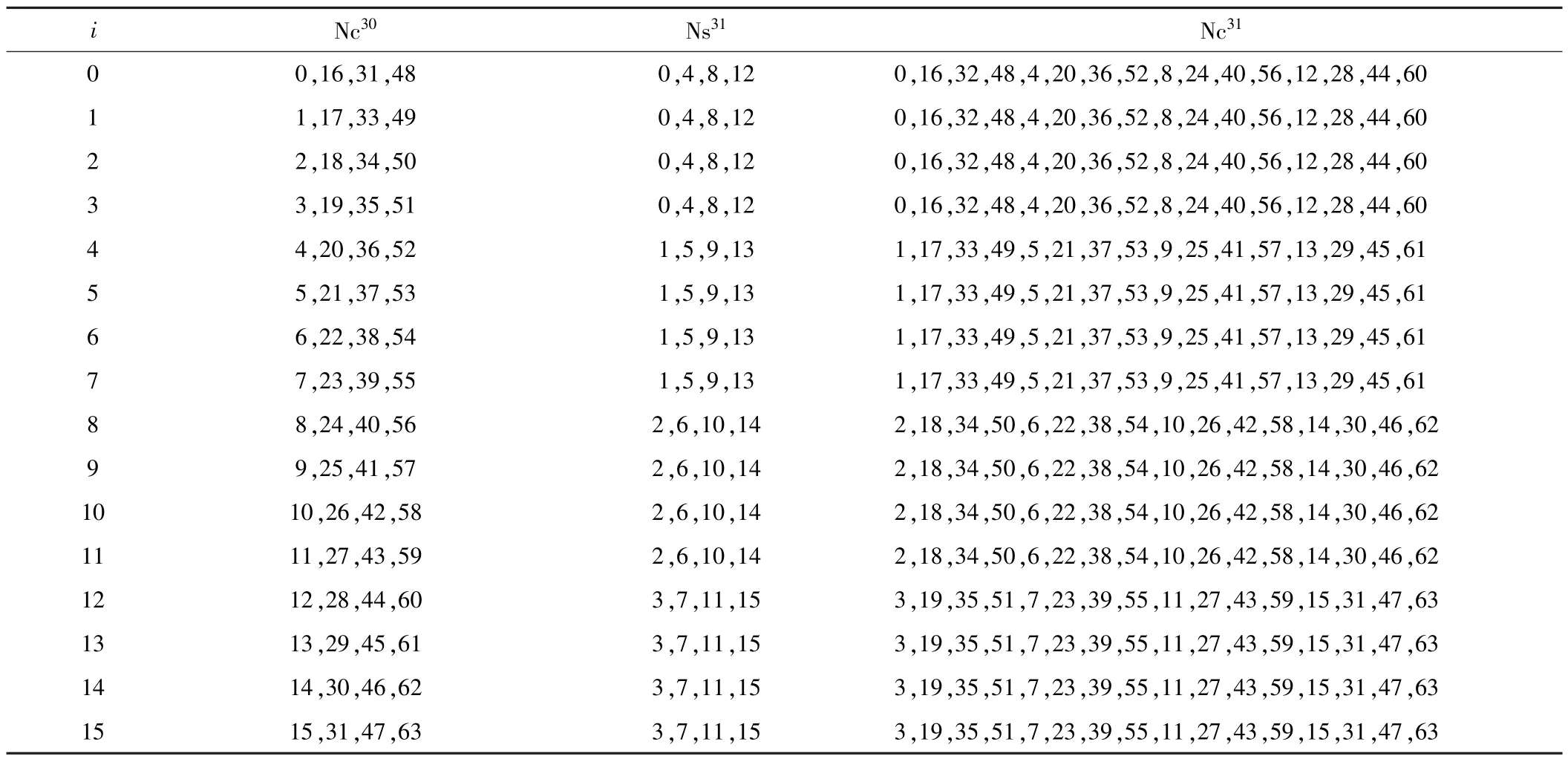
表2 故障传播路径表

由表2可知,当在第30轮产生一个单字节故障时,至多会影响第31轮的4个S盒的输入,因此影响至多16比特位的S盒输出。同理可得,当产生故障字节数为i(0≤i≤15)个时,则会影响下一轮16个S盒的输入,并且影响64比特位的S盒输出。利用上述故障传播路径,将有利于进行差分故障分析。

2.2 PRESENT算法S盒差分特征

在差分故障攻击中,最为核心的步骤就是根据差分来计算每个S盒可能的输入,为

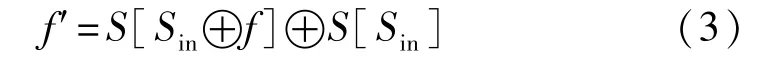
攻击者可以通过已知输出差分f构建S盒输入差分查询表,如表3所示。通过差分查询表来寻找可能的输出差分f,最后通过式(3)求得S盒的输入值Sin。相比于以往的通过穷举的方式寻找Sin,利用查表方式能够快速地找到f并且求得Sin,减少针对S盒输入值的穷举量,缩短攻击时间。

表3 差分S盒特征

表3仅仅给出了每个S盒输出差分只有1位为1的情况,然而在实际情况中每个S盒的输出差分可能有4个位为1,需要根据实际的输出差分来找对应的输入差分。

3 PRESENT算法的随机差分故障攻击

利用PRESENT算法的故障传播特性,可设计如下方案对其实施随机差分故障攻击,具体过程如下:

步骤一 首先随机选取一组明文,将明文在密钥K的情况下进行加密,获取对应的密文C,并且利用示波器采集加密过程中产生的能量信号并转化为能量曲线。将采集到的曲线进行预处理,并把预处理后的曲线结合PRESENT算法的流程进行分析,进而确定算法的第30轮和第29轮的运行时间段,方便后续的故障注入。

步骤二 在智能卡运行期间进行电压故障注入获得错误密文。

(1)根据步骤一采集到的曲线,确定第30轮、29轮的位置,并且在这两轮进行故障注入,进而得到错误密文C*。

(2)将正确密文和故障密文进行异或得到差分密文diffC。

(3)由故障传播路径,可以根据得到的差分密文diffC,通过P盒的逆运算P-1反推出第31轮的16个S盒的输出差分diffP31。

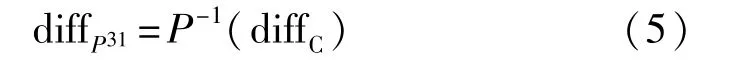
(4)若攻击者对每一个满足条件的输入差分都进行分析,会得到S盒输入集合M{Sin1,Sin2…Sinn},由于S盒的输入为4位,因此M集合的最大下标为16。表4是输出差分固定的情况下,输入差分和S盒输入之间的关系表。

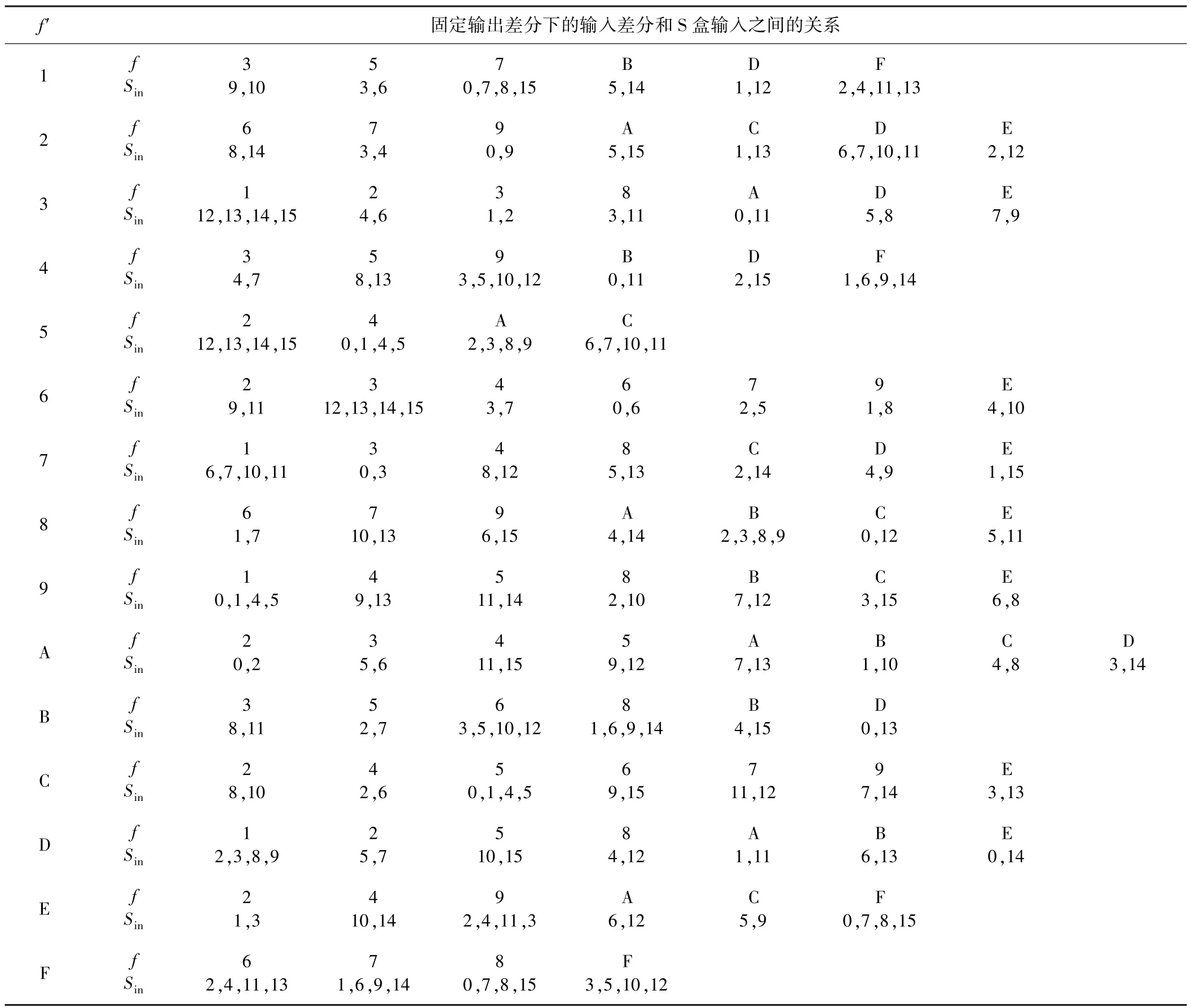
表4 PRESENT算法S盒输入特征表

由表4可知,当输出差分固定时,如果对单个S盒进行分析,那么集合M中会有16个不同的值,显然这样的攻击是无效的。针对这一问题,提出如下的解决方法:

①由表2可知,若将连续相邻的4个S盒分为1组,则1组S盒经过1轮P置换后会影响相同的4个S盒,因此可以采用并行处理的方式同时处理4个S盒,减少攻击所需要的时间。

②由上述条件,攻击者对1组即4个S盒同时进行差分分析,根据4个S盒已知的输出差分(若其中的某些S盒的输出差分为0则可忽略这些S盒),找到候选输入差分交集G。假设有两类输出差分分别为1、4,则对应的输入差分候选集为F(1)={3,5,7,B,D,F},F(4)={3,5,9,B,D,F},交集G={3,B,D,F}。结合表4、表5给出了F(1)与其他输入差分候选集F(n)(2≤n≤15)交集的情况,通过寻找输入差分的交集能够减少Sin的搜索范围。

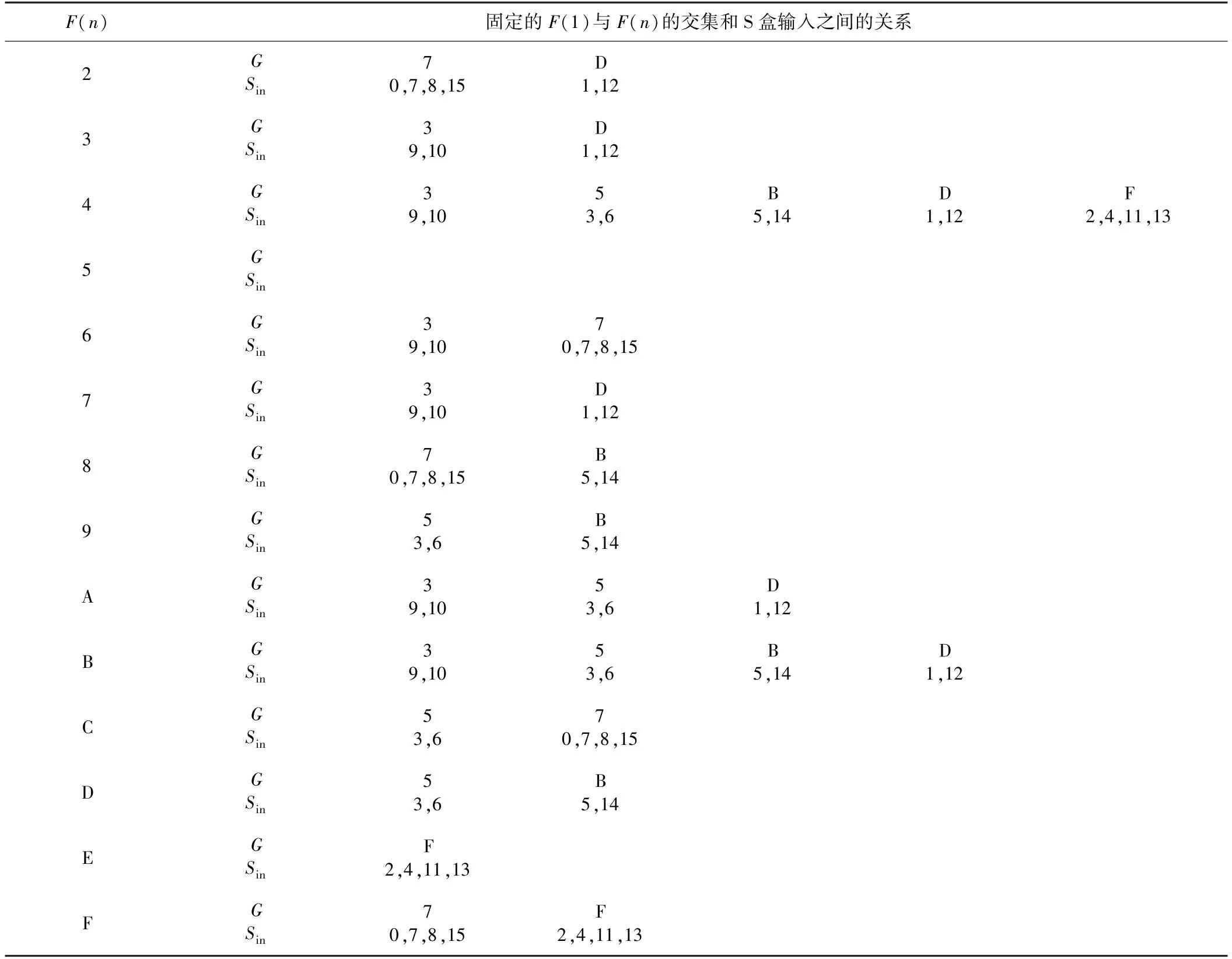
表5 局部S盒输入特征表

③由②可知,已经对S盒的输入进行了筛选,若筛选出来的输入差分包含了正确的输入差分值,那么一定可以得到S盒的正确输入,式(6)为S盒正确输入的概率计算公式。

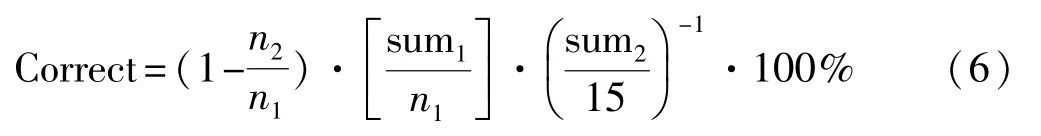
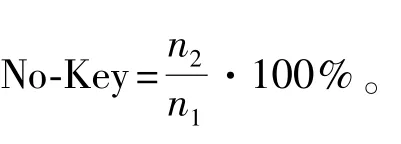
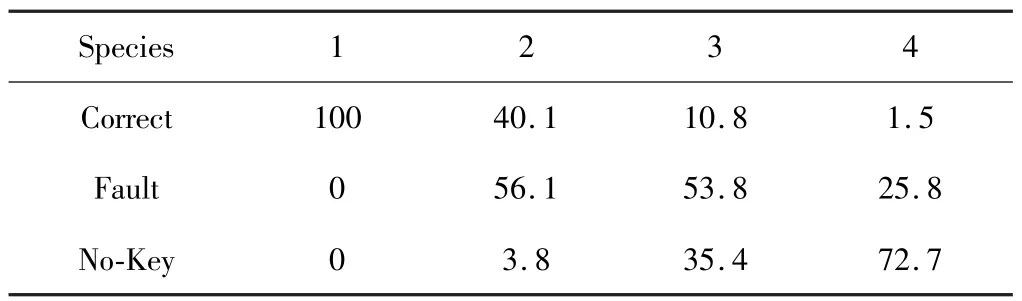
表6 S盒正确输入概率表 单位:%

表6中Species代表4个S盒中正确输入差分的种类,Correct代表当前S盒正确输入出现的概率。Fault代表出现错误输入的概率,No-Key代表不会得到输入的概率,由表6可知若4个S盒中只有一类正确的输入差分,那么正确的输入差分一定包含在G中,则一定会出现正确输入。若有两类正确的输入差分,则会有40.1%的概率出现正确的输入。此时虽然得到错误输入的概率为56.1%,但是在这56.1%概率中包含了15种错误的输入,因此每种错误输入的概率为3.74%,远低于正确输入的概率。同理三类正确输入差分的正确输入概率为10.8%,四类为1.5%。

(5)根据上述内容,对G集合中的候选输入差分diffsin进行遍历,由式(7)可以找出所有候选的S盒输入值 Sin。

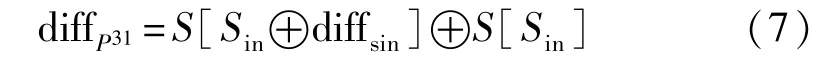
(6)由计算得到的Sin,根据式(8)可以恢复出该S盒对应的4比特位密钥候选值。

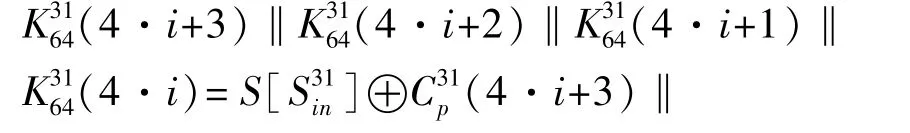
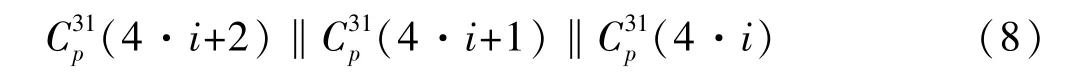
(7)候选输入筛选。首先设置一个长度为16的数组key[16][16],并且初值都0,key[16][16]={{0,0…0},{0,0…0}…{0,0…0}},数组key中的行代表第0～16个S盒,列下标表示16个可能的输入值。将式(8)计算出的候选输入,按照列下标匹配的方式存入到数组key中,并且对应位的数值加1。通过分析多条故障数据,找到二维数组每一行的最大值,最大值的下标就是当前S盒的正确输入,从而恢复出第31轮的64位轮子密钥。

步骤三 根据上述恢复出的第31轮的轮子密钥,逆推可以得到第30轮的密文,重复(1)至(7)的步骤恢复出第30轮的轮子密钥。利用,通过密钥编排算法恢复出主密钥K。

步骤四 主密钥密钥恢复。每一轮的主密钥长度为80bits,记为k=[k79k78…k0],轮计数器r用二进制表示(r4r3r2r1r0)2,由密钥扩展算法可知,K30经过左移61比特位后,此时第31轮80比特的最后16比特位为k＇=k34k33k32…k20k19,而该16比特位在K30的前64比特位中,由攻击出的第30轮64比特密钥K30,可以获得k＇的具体值。经分析经过密钥扩展算法k＇只有一位会产生变化即k34=k348r0。根据已经恢复k31的64比特密钥以及上述推出的k＇,可以推出最后一轮的80比特主密钥

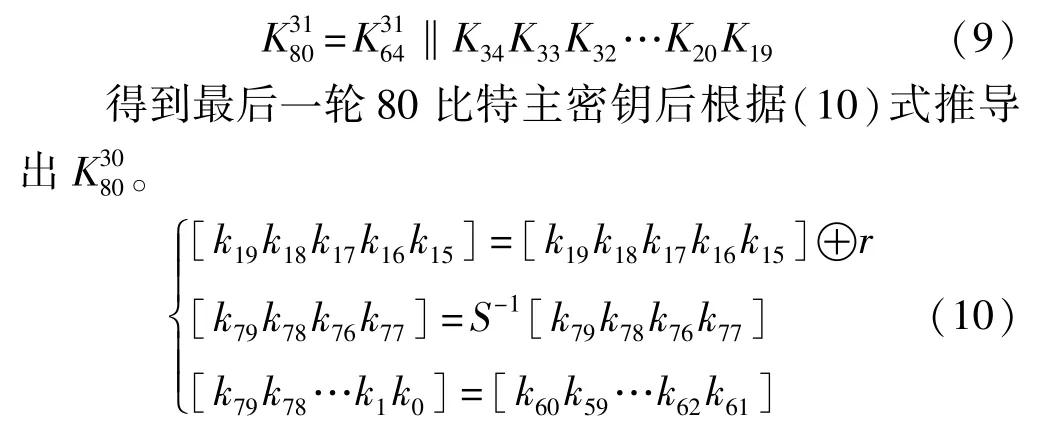
式(10)中第一步为当前主密钥的k19k18k17k16k15与轮计数器进行异或,之后进行S盒的逆运算,最后右移61比特从而得到第30轮的主密钥。同理,可以推出初始的80比特主密钥。通过上述对密钥扩展算法的缺陷分析,攻击者不用通过穷举最后16 bits的方式也可恢复主密钥,提高了主密钥恢复效率。

4 攻击实验与分析

使用智能卡、VC Glitcher、Inspector、示波器等设备进行正确密文和故障密文的采集。选择初始明文为0xc 0x7 0x3 0x9 0xd 0x7 0xe 0xa 0xf 0xa 0xe 0x4 0xe 0xd 0xa 0x3,初始密钥为0xf 0xf 0xf 0xf 0xf 0xf 0xf 0xf 0xf 0xf 0xf 0xf 0xf 0xf 0xf 0xf 0xf 0xf 0xf 0xf,整个实验过程包括信息采集、故障注入、故障分析、复杂度分析以及实验结果分析。

4.1 数据采集

首先采集智能卡在运行时的能量曲线并且记录正确的密文,图3为示波器上采集到的能量曲线。

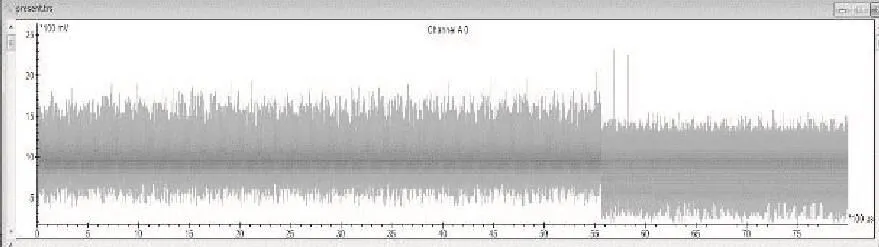
图3 能量曲线

图4为采集到的明文和密文信息,C7 39 D7 EA FA E4 ED A3为采集到明文信息,35 75 04 0B 4F D5 85 BC为采集到的正确密文信息,90 00代表标识位表示智能卡返回数据成功,其余数据代表对智能卡下发的指令。

图4 正确密文信息

4.2 故障注入

对采集到的能量曲线首先进行信号处理,确定PRESENT算法第29轮、第30轮的时间。由图3可知5000～5400 μs为第29轮、第30轮的时间。利用 VC Glitcher在PRESENT算法的第29轮、第30轮分别进行随机故障注入,故障注入的具体位置和故障注入的字节数未知。图5是故障注入后返回的部分故障密文,其中黑框部分为产生的故障密文。

图5 故障密文

4.3 故障分析

根据攻击方法,首先对第30轮的故障密文进行差分分析,恢复第31轮的16个S盒的密钥,图6是实验结果图。

图6 第30轮故障密文分析

同理根据第29轮的故障密文恢复出第30轮的轮子密钥,并且根据两轮轮子密钥恢复初始的80 bits主密钥,图7是实验结果图。

图7 第29轮故障密文分析

通过式(10)可恢复初始80bits主密钥为:15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15。

由上述实验结果可知,轮密钥攻击平均时间为1000 ms,恢复出的主密钥为15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15 15。与初始设定的主密钥一致,达到了攻击的目的,证明文中提出攻击方案的有效性。

4.4 复杂度分析

根据故障传播路径对攻击方法进行重新设计,相比于传统的分析方法或者已有针对PRESENT算法的差分故障攻击方法具有明显的优势。传统的密钥攻击方法大多数采用的是穷举密钥,由于PRESENT算法的轮子密钥长度为64bits,若采用直接穷举密钥搜索,则轮密钥的攻击复杂度为264。而文献[9]则是采用依次扩展的方法,根据每一轮的中间匹配状态来进一步的降低搜索空间,攻击复杂度为231。根据PRESENT算法的故障传播路径,采用多字节故障模型的方法,通过输入差分的交集来寻找正确密钥。复杂度C如下:

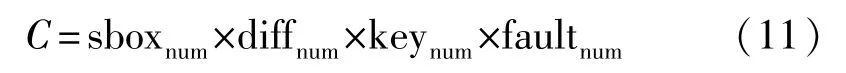
其中sboxnum表示S盒的数量,值为16。diffnum代表每个S盒输出差分一定的情况下的输入差分数量,经计算分析diffnum的取值范围为4≤diffnum≤8。keynum表示每个S盒输入差分对应的候选输入的个数,候选输入的个数范围为0≤keynum≤4。faultnum代表恢复该轮轮子密钥所需要的故障密文数,经过实验分析,平均300条故障密文就可以恢复当前的轮子密钥。综上所述,恢复出轮子密钥的复杂度C=218。

5 结束语

利用优化后的差分故障攻击方法,对写有PRESENT算法的智能卡进行随机故障注入,并且对得到的故障数据进行分析,实验结果证明方法具有有效性。与现有的针对PRESENT算法的单字节故障注入相比,本文提出的方法没有限定故障注入的位置和故障注入的数量,打破了以往研究对故障诱导的限制,降低了对故障注入设备的要求,为针对SPN结构分组密码算法的故障攻击提供了新思路。并且轮密钥的攻击复杂度由231降低到218,攻击时间降低了19000 ms,效率也得到了极大的提高。