基于CNN-BPR的S-Box功耗随机化侧信道攻击
曹家华, 吴 震, 王 燚, 王 敏
(成都信息工程大学网络空间安全学院,四川 成都 610225)
0 引言
密码算法在理论上得到了密码学家的严格审查,但是从物理实施的角度来看,密码算法仍然很脆弱,密码设备的运行过程中不可避免地存在着电磁辐射、能量消耗、时间变化或之类的侧信道泄露。侧信道攻击(side channel attack,SCA)就是一种利用这些侧信道泄露来破解秘密信息的攻击方法。Kocher[1]根据操作私钥所需要的时间,实现了对RSA算法的侧信道攻击,大量研究成果表明无保护措施的密码设备基本难以抵抗侧信道攻击。能量分析攻击属于侧信道攻击中应用较为广泛的一种,其中简单能量分析[2]、相关性能量分析[3-4]和差分能量分析[5]常用于直接对目标设备的功耗信息进行攻击。而模板攻击[6]则需要攻击者拥有与目标设备相同类型的设备,并假设功耗噪声服从高斯分布来构造汉明重量模板或中间值模板,然后利用这些模板对密钥进行恢复。
S-Box功耗随机化[7]是一种抵抗能量分析攻击的常见策略,主要分为能量值随机化和时间随机化。能量值随机化方法以添加掩码来实现,通常可以使用高阶差分能量分析[8]完成攻击。时间随机化方法旨在打乱中间值出现的时间点,导致攻击者无法有效捕获中间值的能量信息,差分能量分析攻击和传统模板攻击方法在面对这类防御手段时往往表现出很差的攻击效果。
近年来,大量实验证明卷积神经网络能够构建更为高效的模板[9]。Cagli等[10]提出了一种卷积神经网络与数据增强相结合的方法,这种方法不需要对齐能量轨迹和选择兴趣点,减少了传统能量分析攻击中的任务量。Benadjila等[11]全面测试了卷积神经网络中各类参数对模板攻击的影响,通过组合每一类参数的最优值,提出了基于VGG-16网络结构的卷积神经网络模型CNNbest,并通过实验证明了CNNbest在ASCAD数据集上的攻击效果要优于传统模板攻击、多层感知器模型和原始VGG-16模型。Zaid等[12]提出了一种使用排序损失函数代替CNNbest中交叉熵损失函数的方案,并验证了该方案能够使CNNbest模型更快地收敛到最佳状态。为有效地构建S-Box功耗随机化的模板,文中将使用卷积神经网络构建基本模型,并从损失函数的角度对其优化。
1 背景知识
1.1 卷积神经网络
卷积神经网络主要通过卷积层、池化层和全连接层实现对输入样本的分类。卷积层通过卷积运算和激活函数将本层输入数据的特征提取出来,然后传递给池化层。池化层通过最大池化或平均池化进行下采样,以此降低卷积层的输出维度,实现模型的平移不变性。全连接层负责在最后对数据进行分类,通过特征加权得到每个类别的置信度分数,然后经过分类函数的计算得到输入样本的类别。在侧信道攻击中通常使用一维卷积和一维池化,计算过程如图1所示。
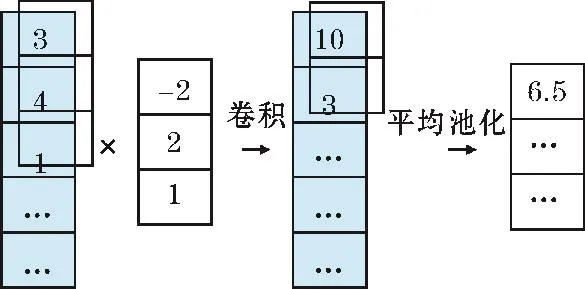
图1 一维卷积与池化
1.2 损失函数
卷积神经网络中除了各层网络结构之外,另一个对模型性能有较大影响的因素是损失函数。损失函数能够表现出模型的预测值和真实值之间的差异程度,使用合适的损失函数,并尽可能降低损失函数的计算结果是优化模型的一种方法。常见的损失函数有平均绝对误差、均方误差以及交叉熵(cross entropy,CE)等,通常模板攻击使用Softmax交叉熵作为损失函数。以AES加密算法为例,以首轮加密中S-Box输出的一个字节为中间值,在明文已知的情况下,该中间值和密钥满足一一映射的关系,因此中间值的概率分布与对应位置密钥的概率分布一致。假设密钥的取值集合为K={0,1,…,255},定义k∈K表示一个猜测密钥,yk表示猜测密钥k对应的真实标签,pk表示猜测密钥k的预测概率,可以得到单个样本的Softmax交叉熵损失:
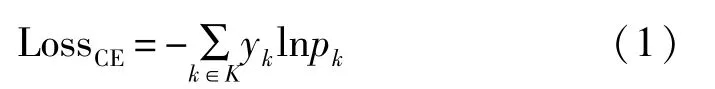
2 损失函数的改进方法
2.1 L2约束的损失函数
卷积神经网络在功耗泄露明显的数据中能取得很好的训练效果,但对于S-Box功耗随机化数据的效果却很差。主要是基于以下两个原因:一是大多数卷积神经网络使用Softmax交叉熵作为损失函数,这无法保证模型学习到的正对之间特征差异较小而负对之间特征差异较大。因此,在泄露信息极少的功耗随机化数据中,不同密钥所带来的功耗差异没有被有效地提取。Softmax交叉熵以最大化同一批样本的条件概率之和来降低模型的损失,但是功耗随机化导致同一批的各个样本识别难易程度相差较大,Softmax交叉熵通过让容易识别的样本范数更大,让难以识别的样本范数更小,从而将损失最小化。如果直接使用Softmax交叉熵损失,很容易让模型只关注随机化离散程度较低的样本,而忽略随机化离散程度较高的样本,从而导致训练出来的模型在攻击数据上的表现很差。
L2范数被广泛应用于机器学习的损失函数正则化[13],可以提高模型的泛化能力,避免过拟合的发生。在卷积神经网络中应用L2范数进行正则化处理,其过程如图2所示。
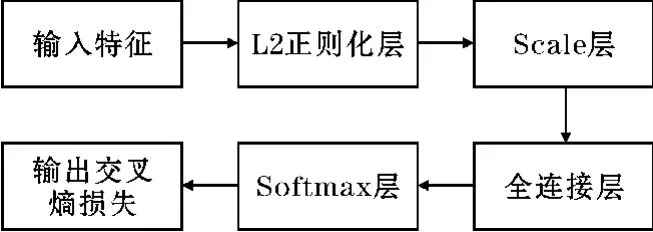
图2 L2正则化过程
图中,L2正则化层将所有样本的特征进行归一化,Scale层对L2正则化层的结果进行α倍的缩放,这样可以降低特征范数对模型的影响,增加正对之间的相似性和负对之间的差异性。同时,更小的特征范数也使模型对简单样本和困难样本的关注程度更相近。
在模板攻击中找出样本所对应的真实密钥是典型的单标签多分类任务。定义真实密钥k*的标签为1,错误密钥的标签为0,即yk在k≠k*时为0,损失值Loss仅受到猜测密钥k=k*的预测概率影响,使用Wk,bk分别表示猜测密钥k在全连接层的权重向量和偏置,X表示输入到全连接层的特征向量,那么可以得到关于特征向量的Softmax交叉熵损失:
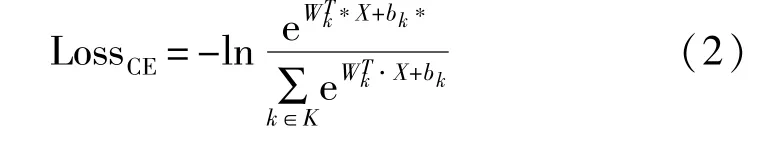
将正则化处理后的X代入式(2),即可得到L2约束的Softmax交叉熵损失函数,计算结果为
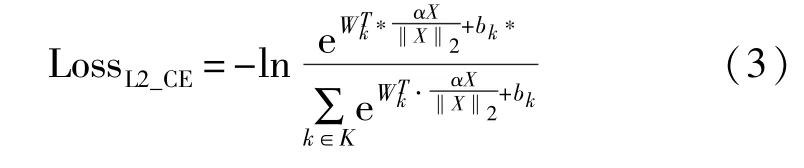
2.2 贝叶斯个性化排序损失函数
贝叶斯个性排序[14](Bayesian personalized ranking,BPR)是推荐系统中一种基于Pairwise方法的排序算法。以商品推荐为例,BPR算法将每个用户对应的所有商品按权重排序,然后向用户推荐排名靠前的商品,以此从极大数量的商品集中推选出更符合用户需要的商品。基于此思想,不拘泥于对真实密钥权重的提升,而是直接对模板攻击中Rank指标进行优化,更适用于分类难度较高的S-Box功耗随机化数据。
Rank指标是一种典型的模板攻击评价标准[15],将模型的预测结果进行排序得到猜测密钥k的排序名次Rank(k),k的排名越靠前,Rank(k)越低,k为真实密钥的可能性越大。当Rank(k*)=1时,表示真实密钥k*的预测结果排在第一位,即成功恢复出了密钥。在卷积神经网络中,把全连接层输出的置信度分数作为猜测密钥k的得分s(k),将所有猜测密钥的得分进行降序排序得到排序名次Rank(k),真实密钥k*的排名Rank(k*)的计算方法为
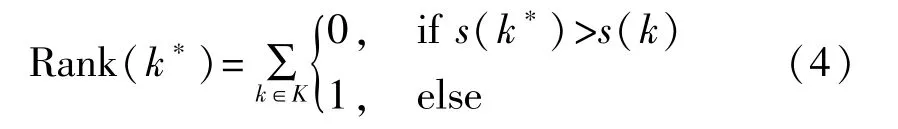
在BPR中k*>tk为能量轨迹t的一个偏序关系,表示k*的真实排名在k的前面,即Rank(k*)
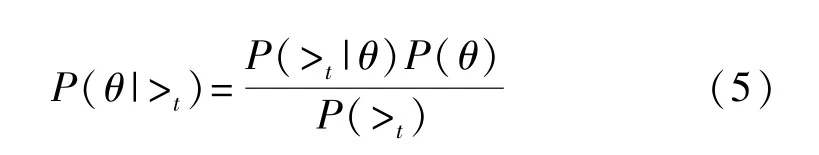
由于能量轨迹的密钥是独立随机的,因此可以得到P(>t)=1/2,根据式(5)可以得到:
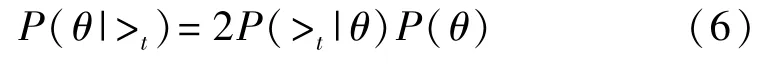
最大化 P(θ|>t)等价于最大化 P(>t|θ)和 P(θ)。对于P(>t|θ),模板攻击中关键是获得真实密钥的排序关系,因此令式(6)的>t=k*>tk,得到:
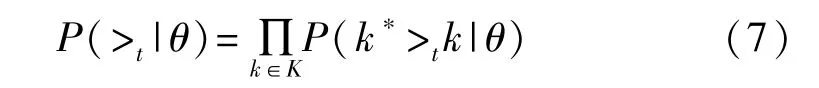
P(k*>tk|θ)表示在参数为θ的情况下,真实密钥比猜测密钥排名靠前的概率。对于k*>tk这一事件,使用卷积神经网络全连接层输出的置信度分数s(k*)-s(k)>0来表示,使用Sigmoid函数来代替发生这一事件的概率,为
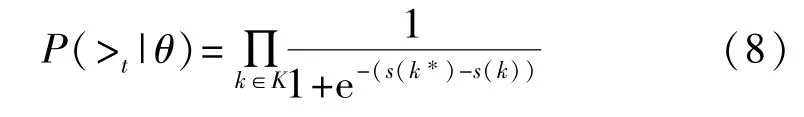
对于P(θ),假设参数θ的概率分布满足均值为0,协方差矩阵为λI的正态分布,那么其对数与成正比。
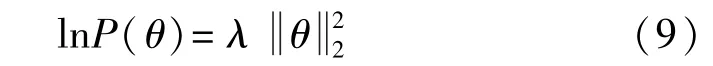
最大化P(θ|>t)等价于最小化其对数的负值,使用 P(>t|θ)和 P(θ)代替 P(θ|>t),得到 BPR 的损失函数:
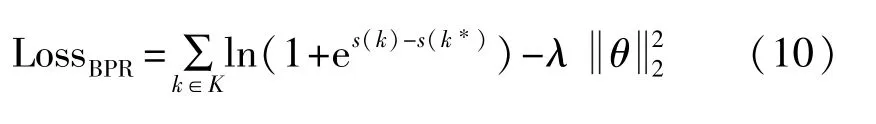
3 模型设计与实验
本文使用的卷积神经网络结构设计如图3所示,输入是包含700个样本点的能量轨迹。卷积层所使用的卷积核大小为11、步长为2,激活函数使用Relu,过滤器数量依次为128、256、512。池化层使用大小为2、步长为2的平均池化。首层全连接层有4096个神经元,激活函数使用Relu。末层全连接层有256个神经元,激活函数使用Softmax。
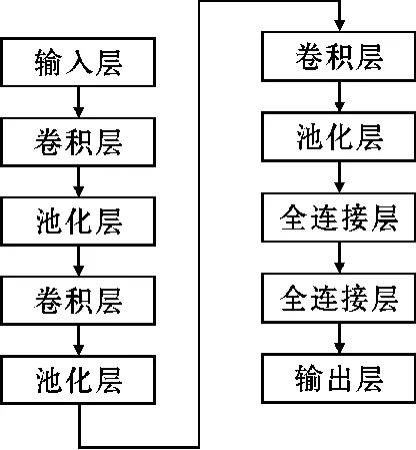
图3 网络结构图
3.1 实验环境及数据
实验环境所使用的卷积神经网络基于Python Tensorflow 2.0进行搭建,然后在搭载了4块NVIDIA Ge-Force RTX 2080 Ti GPU的服务器上训练模板并进行攻击。
实验数据使用法国国家网络安全局侧信道数据库(ANSSI SCA Database,ASCAD)提供的ASCAD.h5和ASCAD_desync50.h5数据。ASCAD.h5由50000条训练数据和10000条攻击数据组成,每一条数据都有700个样本点,包含了AES第一轮加密的第三个S-box输出操作的功耗信息。ASCAD_desync50.h5由ASCAD.h5进行非对齐操作后得到,具体实现为将ASCAD.h5中的每一条数据向左随机偏移,其中偏移量β∈{0,1,…,50}。
3.2 实验分析
对图3所示的卷积神经网络结构分别应用Softmax交叉熵损失函数、L2约束的损失函数和BPR损失函数,所有模型均训练150个Epochs,其中L2约束的损失函数中缩放倍数 α=2,BPR损失函数中 λ=0.0001。通过Rank值随攻击能迹数的变化来表示攻击效果,当攻击能迹数相同时,Rank值越低则表示模型攻击效果越好。
图4、图5是当选取30000条训练能迹数时,3种损失函数模型在有随机偏移和无偏移的数据集上的攻击效果。根据对比可以看出,BPR损失函数和L2约束的损失函数在无偏移的数据集上能够更快地降低Rank值,但三者成功恢复密钥需要的攻击能迹数相近。当数据存在随机偏移之后,BPR损失函数和L2约束的损失函数产生的攻击效果明显优于传统Softmax交叉熵损失函数。其中,BPR损失函数的效果最好,能够以582条攻击能迹数达到Rank值为1的攻击效果,而另外两种损失函数达到这一效果则需要800条左右的攻击能迹。
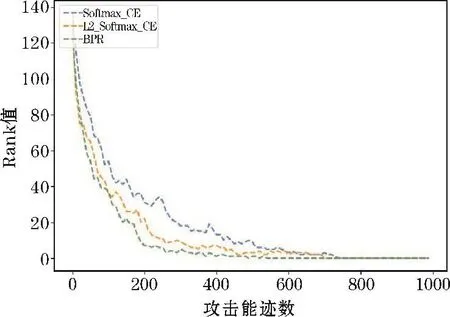
图4 训练能迹数为30000,偏移量β=50
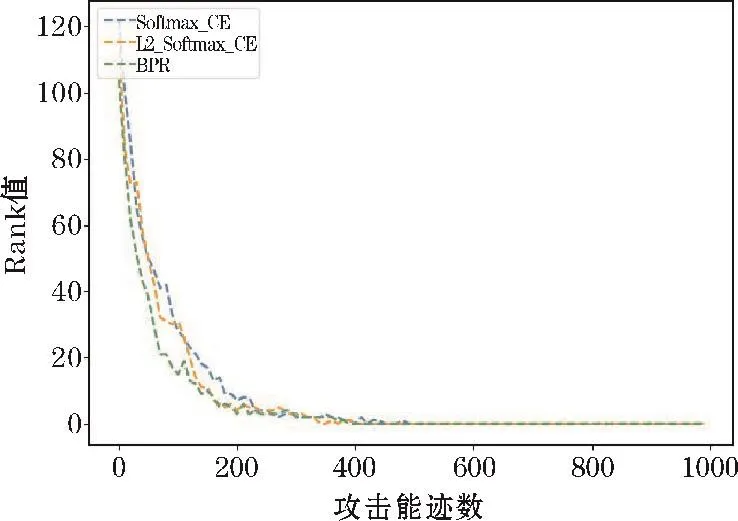
图5 训练能迹数为30000,无偏移量
对训练所使用的能迹数量进行增加,然后对比3种损失函数在ASCAD_desync50.h5数据集上的效果,记录攻击阶段Rank值等于1时所需要的最少能迹数量,其结果如表1所示。
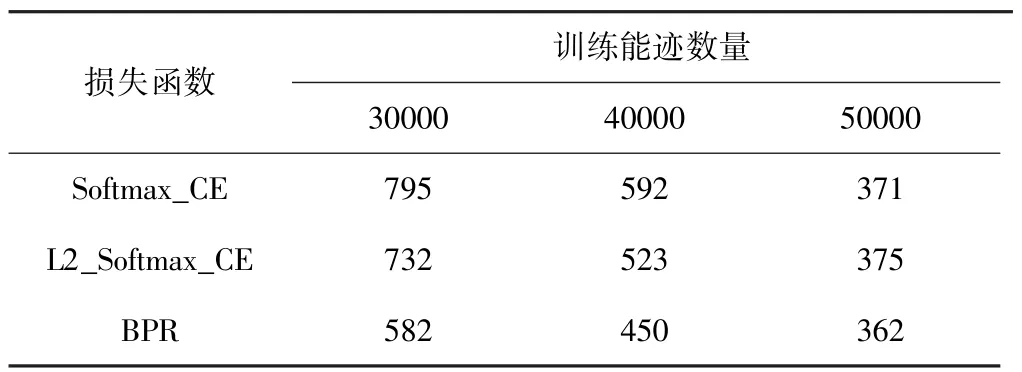
表1 攻击成功所需的能迹数量
由表1可知,当训练能迹数量足够大时,3种模型的攻击效果比较接近,但是随着训练能迹数的减少,Softmax交叉熵损失函数模型的攻击效果下降得更加明显,而BPR受到的影响则相对较小。当侧信道攻击中无法大量捕获到目标设备的功耗时,优化Rank值的BPR模型比Softmax交叉熵模型更适用于神经网络的模板攻击。
综上,在基于Rank值的评价标准下,本文提出的CNN-BPR对于功耗数据的随机偏移具备一定的抵抗能力。在训练样本数较少的情况下,BPR和L2约束的损失函数由于正则项的影响,训练出的模型具有更好的鲁棒性,在噪声较大的数据集上优于传统Softmax交叉熵损失函数。
3 结束语
基于交叉熵的卷积神经网络在分类任务中,关注的是每一个样本的真实标签被预测到的程度,真实标签的预测概率越大则效果越好,当需要检测某一个样本的种类时,通过这一关注点能够很好地构造模型。然而,使用卷积神经网络进行模板攻击的任务目标却不完全与分类任务相同。这是因为在模板攻击中,攻击阶段的样本通常使用同一密钥,即攻击阶段的样本具有相同的标签。因此,只需要使真实密钥在攻击样本集合上的综合概率最大即可,这一目标通过尽可能地提高真实密钥的Rank值来达到。本文提出了一种基于BPR损失函数的卷积神经网络模型CNN-BPR,并在ASCAD.h5和ASCAD_desync50.h5这两组数据集上进行了验证。实验结果表明,BPR损失函数相较于交叉熵损失函数能够构造鲁棒性更高的模型,且能有效减少成功恢复密钥所需要的攻击能迹数量。
虽然提出的CNN-BPR模型相比使用交叉熵损失函数的模型有一定的优化,但当训练能迹数量充足时,过拟合不再是约束模型性能的主要问题,因此正则化损失函数带来的优化效果并不明显。在这种情况下,如何继续改善网络模型,还需要进一步研究。

