基于随机故障注入的GOST差分故障攻击方法
蔡承伯, 杜之波, 吴 震, 李圣泉, 江 楠
(1.成都信息工程大学网络空间安全学院,四川 成都 610225;2.国电南京自动化股份有限公司 南京华盾电力信息安全测评有限公司,江苏 南京 211106)
0 引言
1977年美国将DES算法确立为数据加密标准(data encryption standard),此后在其他国家和地区出现了一系列DES替代算法,1989年苏联发布在GOST 28147-89标准中[1]的GOST分组加密算法就是其中之一。2015年俄罗斯联邦制定了GOST34.12-2015加密标准,并于2016年1月1日起生效,该标准包含了两种对称加密算法,其中之一就是GOST,在新标准中又被称为Magma[2]。针对GOST的密码分析工作主要有线性分析[3]、差分分析[3-4]和滑动攻击[5],但这些关于GOST的数学安全性分析都脱离不了“降低代数复杂度”的特定框架,这意味着在现实条件下很难对其构成真正的威胁。
差分故障攻击(differential fault attack,DFA)是一种常见的侧信道攻击技术,在1997年由两位以色列的密码学家Biham和Shamir提出[6]。其核心思想是通过在密码设备运行过程中导入故障值,然后结合正确和错误密文计算出差分值,最后利用密文差分值和相关密钥之间的关系进行密钥破解。利用该方法能够恢复出多种密码算法的密钥,例如 AES[7]、SM4[8-10]、FeW[11]、PRESENT[12]等。在GOST的差分故障攻击研究中,文献[13]首次给出GOST的差分故障攻击方法,研究人员选择在倒数第二轮的右半部分导入半字节的随机故障来攻击最后两轮子密钥,注入64次就能成功恢复主密钥。文献[14]提供了两种GOST的差分故障攻击方法,共同点是都采用单字节随机故障模型,其主要区别是攻击最后一轮子密钥时,方法1诱导的故障位置在最后一轮的右半部分,方法2则将故障位置扩展至最后的两轮。仿真实验结果表明在两种模型下恢复主密钥分别需要72和36个故障。上述攻击方法均有两个共同的现实问题:(1)攻击要能成功执行,攻击者必须将故障导入特定的位置,在实际攻击中严格的前提条件导致该方法很难实施,因此针对GOST的差分故障攻击目前尚没有公开发表的实测结果。(2)故障数据都是特定的仿真数据,对错误密文筛选的过程进行回避。实际上,故障注入产生的错误数据并不是全部有效,攻击者需要根据单次攻击的具体情况对错误密文进行筛选。
针对GOST算法的研究现状,提出一种更符合实际攻击的GOST差分故障攻击方法。首先故障诱导时不再局限于某个位置,而是扩大至算法的最后八轮,这不仅极大地降低了故障诱导的难度,还扩大了故障诱导的范围。其次密钥筛选方法让攻击者筛选错误密文时不再需要特定的错误密文,只需在故障分析时简单筛选错误密文即可成功攻击主密钥。
1 GOST算法介绍
1.1 GOST加密算法
GOST分组加密算法是对称加密算法,属于Feistel网络结构,明文分组采用的是64比特,密钥长度采用的是256比特,总共迭代32轮。在每一轮中,F函数的输出与轮输入的左半部分进行异或运算成为新的左半部分,然后左右交换成为下一轮的输入,最后一轮左右不交换。整体轮结构如图1所示。
1.2 GOST的F函数
F函数如图2所示,由3个部分组成。首先右半部分数据与该轮子密钥进行模232加操作,然后将32比特结果分为8个4比特分组,依次进入8个S盒。最后将8个S盒的输出重组成32比特字,循环左移11比特得到输出结果[15]。

图2 GOST的F函数
GOST在GOST 28147-89标准中没有特定的S盒,但是在最新标准GOST 34.12-2015中填补了对S盒的定义,并且是固定唯一的。具体见表1。
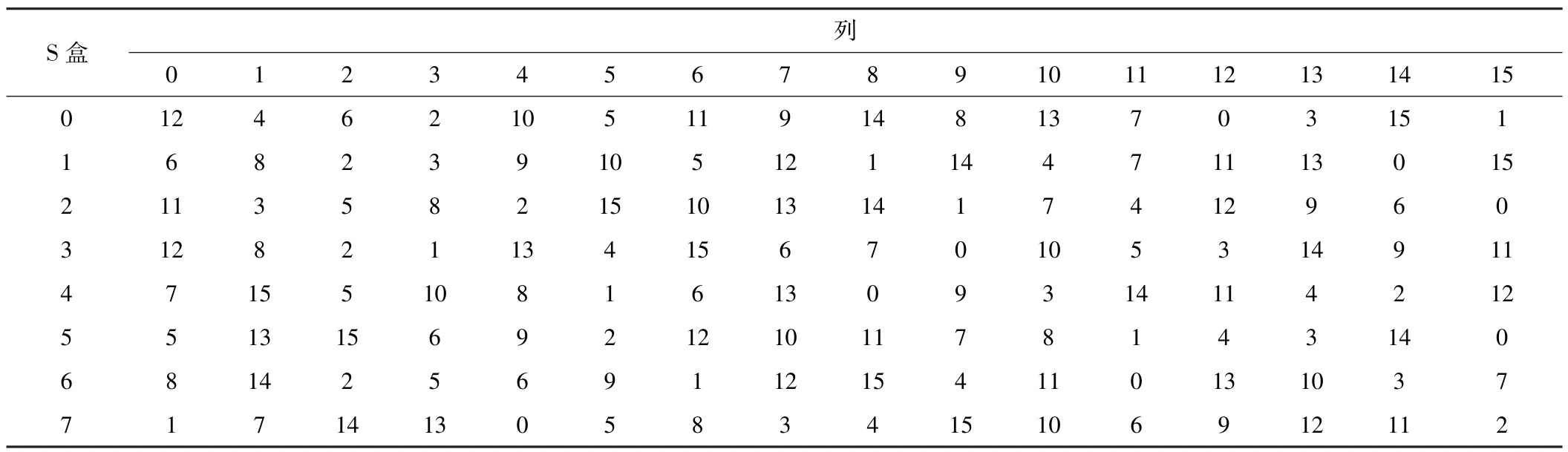
表1 GOST 34.12-2015提供的S盒
1.3 密钥编排
将256比特的主密钥K分为8组32比特的子密钥 K0、K1、K2、K3、K4、K5、K6、K7,第 i轮使用的子密钥如表2所示。

表2 密钥编排
2 GOST算法的DFA研究进展
2.1 DFA
一般情况下,故障攻击分为以下4个步骤:选择合适的故障模型;针对故障模型选择合适的注入手段进行故障注入;对获得的错误密文样本进行选择性筛选;对筛选后的错误密文样本进行故障分析。在进行故障分析时,如果采用了差分分析法,那么这种故障攻击就称为差分故障攻击。
差分故障攻击主要是在密码芯片运行的过程中进行故障诱导,利用得到的错误密文和正确密文计算出输入差分和输出差分,再根据算法结构建立差分方程,求解差分方程得到轮密钥的候选值集合,通过多次攻击缩小候选值范围,最终得到唯一正确的轮密钥。攻击原理如图3所示。
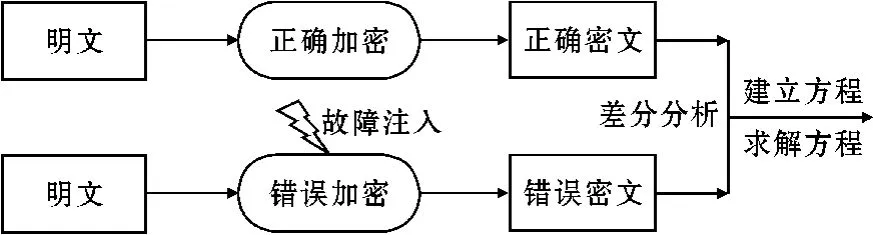
图3 DFA原理
2.2 GOST已有DFA方法
2012年Jongsung Kim[13]首次提出了一种GOST密码差分故障攻击方法,其攻击原理是利用GOST独有的故障传播路径将随机的半字节故障分别注入到R30的第7个、第8个、第6个、第5个、第4个、第3个、第2个、第1个半字节中,一次性攻击最后两轮的子密钥。理论上基于此模型恢复K31和K32需要16个错误密文,恢复主密钥需要64个错误密文。该方法具有以下特点:(1)攻击选用的故障模型相对严苛,注入半字节随机故障时,攻击者虽然不控制故障的取值,但是需要控制故障的位置;(2)在实际攻击中利用此方法攻击最后八轮子密钥时,攻击K31和K32时需要进行一轮故障注入,攻击K29和K30时需要重新进行一轮故障注入,换言之恢复主密钥总共需要四轮故障注入;(3)在单轮的故障注入后还需要对错误密文进行筛选,并且至少选出16个符合要求的错误密文。
2015年陶智[14]提出了两种GOST密码差分故障攻击方法,攻击采用的均为单字节随机故障模型。方法1采用的攻击策略是将随机单字节故障注入到最后一轮R31的第1个、第2个、第3个、第4个字节中,通过差分分析来恢复最后一轮子密钥的某一字节,最后通过重复攻击来恢复最后一轮子密钥的所有字节。但是这种方法与文献[13]提出的方法一样,存在故障导入精准率太低的问题。因此,方法2在方法1的基础上提出了一种理论上的改进策略,在攻击最后一轮子密钥时将故障注入的范围扩大为最后两轮,使用该策略在进行差分分析前,要根据密文差分和故障注入位置的关系来判断故障注入的轮数和字节位置。如果不符合要求则需要重新进行故障注入,直到获取的错误密文数量满足攻击成功所需的错误密文数量为止。仿真实验结果表明,使用这两种不同的方法进行攻击分别需要72个和36个错误密文。
3 基于随机故障注入的DFA
3.1 符号说明
本文使用的符号说明如表3所示。

表3 符号说明
3.2 基本过程
基本过程如下:(1)选择一组初始明文,使用密钥K进行加密得到正确密文。(2)在主密钥不变的情况下再次对这组明文进行加密,在后八轮任意位置进行随机故障注入,完成后获取一定数量的故障密文,对故障密文进行简单筛选。随后通过差分分析,结合密钥筛选方法依次恢复出后八轮子密钥 rk31、rk30、rk29、rk28、rk27、rk26、rk25、rk24。 (3)结合密钥编排的逆方法恢复出256位主密钥K。
3.3 攻击过程详述
步骤1 采集正确密文信息和泄露的能量曲线。
选择初始明文P(L0,R0)=FE DC BA 98 76 54 32 10,在密钥为K的GOST算法下进行加密,得到正确密文C(XL,XR)。同时用示波器连接插入智能卡的读卡器,对泄露的能量曲线进行采集,获取最后八轮的运行时间,以便确定导入随机故障的位置,如图4所示。

图4 随机故障注入
步骤2 执行随机故障注入,获取一定数量的错误密文。
(1)使用密钥K再次对明文P进行加密,根据步骤1获取的能量曲线确定最后八轮的运行时间段,对最后八轮执行随机故障注入,获取一定数量的错误密
(2)对获取的错误密文进行一个简单筛选。筛选出与正确密文长度一样,但值不一样的错误密文。
步骤3 攻击第32轮。

ST为算法正常运行时S盒的正确输入,SF为故障注入后S盒的错误输入;记ST、SF、Sin从左到右对应的4个字节分别为ST[x],x=0,1,2,3、SF[x],x=0,1,2,3、Sin[x],x=0,1,2,3,则有:

(3)使用密钥筛选方法,计算出第32轮子密钥rk31。
步骤4 攻击剩余七轮的子密钥,每轮需要的错误密文均来自于步骤2。在步骤3的基础上对GOST最后一轮解密,获得第31轮正确的和错误的轮输出,重复步骤3的操作,恢复出rk30。以此类推恢复出rk29、rk28、rk27、rk26、rk25、rk24。
步骤5 根据密钥编排的逆方法,恢复主密钥K。
3.4 密钥筛选方法
步骤3(3)提到的密钥筛选方法具体如下:
(1)将256个候选字节从小到大放入数组kbyte,同时设置一个全为0的二维数组K[4][256],其中4代表该轮子密钥从左到右的4个字节,256对应kbyte的256个候选字节。

(2)如果Sout不为0,就将256个 kbyte依次带入等式(9)和式(10),当式(11)成立时,二维数组对应的位置自增1,不成立则不变。例如分析第一个错误密文时,x=0对应的kbyte等于0x00和0x03时使式(11)成立,其余的不成立,则K[0][256]={1,0,0,1,…,0,0},其他3个字节同理。
(3)分析完所有错误密文后,找到二维数组K各行最大的值,其对应位置的候选字节即为步骤(4)需要的字节。例如针对第一个字节,K[0][256]={5,18,5,1,…,88,…,0,0},最大值88位于数组元素编号121处,则对应的候选字节为0x7C,其他3个字节同理。
(4)记步骤(3)得到的4个字节依次为 kbyte,0、kbyte,1、kbyte,2、kbyte,3,因为模 232加法运算有可能出现进位的情况,所以这里得到的kbyte,0、kbyte,1、kbyte,2不一定是子密钥正确的前3个字节,因此需要对这3个字节作二次处理,具体如下:
如果kbyte,3+XR[3]>0xFF,则kbyte,2=(kbyte,2-1)mod 28;如果kbyte,2+XR[2]>0xFF,则kbyte,1=(kbyte,1-1)mod 28;如果 kbyte,1+XR[1]>0xFF,则 kbyte,0=(kbyte,0-1)mod 28。最后将处理后的 4 个字节 kbyte,0、kbyte,1、kbyte,2、kbyte,3重组为32比特的字,得到正确的rk31。
4 实验与分析
4.1 实验环境
所需要的实验环境如表4所示。
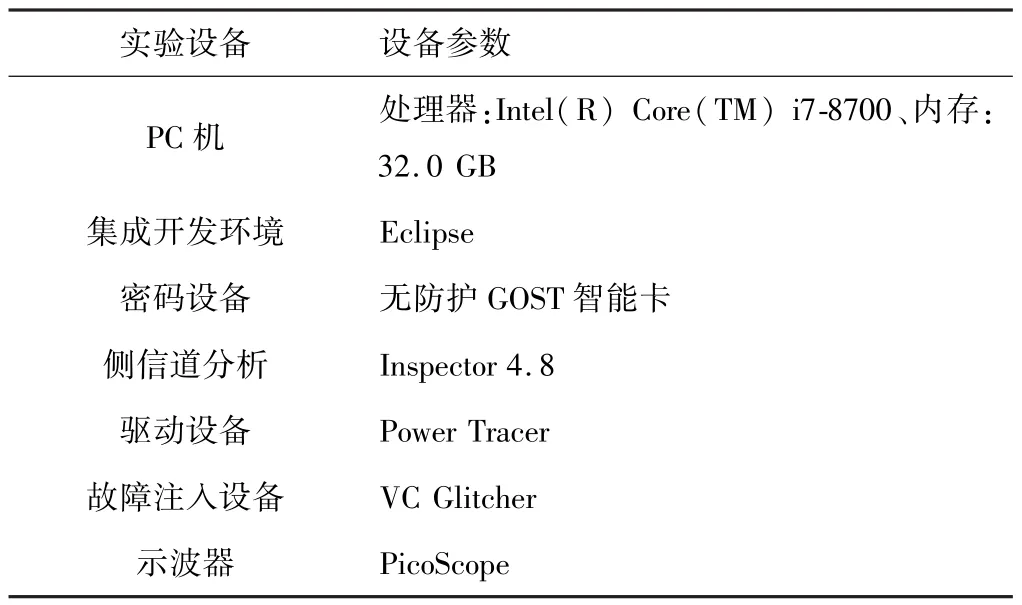
表4 实验环境
4.2 原始信息采集
首先设置初始明文为:FE DC BA 98 76 54 32 10,然后采集GOST算法智能卡正常工作时产生的能量曲线和输出的正确密文信息,对应3.3小节的步骤1。图5是示波器采集到的能量曲线,横轴表示算法的运行时间,纵轴表示运行过程中泄露的功耗。图6是采集到的正确明文和密文信息:FE DC BA 98 76 54 32 10 4E E9 01 E5 C2 D8 CA 3D。
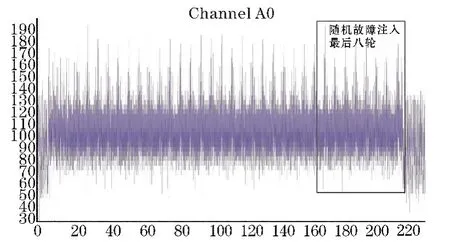
图5 能量曲线

图6 正确明文和密文信息
4.3 故障注入
首先通过观察图5能量曲线的运行时间轴,以确定GOST算法的最后八轮运行区间,在实际攻击中可以选择最后九轮或者最后十轮进行攻击,只要包含最后八轮即可。然后对选中的运行区间实施1000次随机故障注入。图7是故障注入后Inspector采集到的部分数据信息,绿色数据是故障注入失败的返回数据;红色数据是故障注入成功的返回数据;矩形框部分是返回的错误密文,一共有240条。最后记录下这240条数据,用于后续差分分析。

图7 返回数据信息
4.4 差分分析
使用3.3小节步骤3和步骤4提出的方法对正确密文以及上述获得的240密文进行攻击。第32轮攻击结果如图8所示,在每4个字节里面,如果单个字节的置信度最高并且明显高于其他字节,那么这个字节就是正确的候选密钥字节。最终第32轮子密钥为:FF EE DD CC。

图8 第32轮结果
攻击剩余7轮,每一轮使用的错误密文与第32轮一致,攻击结果见表4。

表4 剩余七轮攻击结果
4.5 结果验证
使用攻击得到的主密钥FF EE DD CC BB AA 99 88 77 66 55 44 33 22 11 00 F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 FA FB FC FD FE FF对同一明文进行加密,得到密文4E E9 01 E5 C2 D8 CA 3D,结果与图6采集的正确密文信息一致,表明攻击成功。同时也证明了本文提出的方法在真实实验环境下能够恢复出主密钥,并且相比现有其他方法,扩大了攻击的故障诱导范围,提高了攻击的灵活性和实用性。表5对各方法的故障诱导位置作了比较。
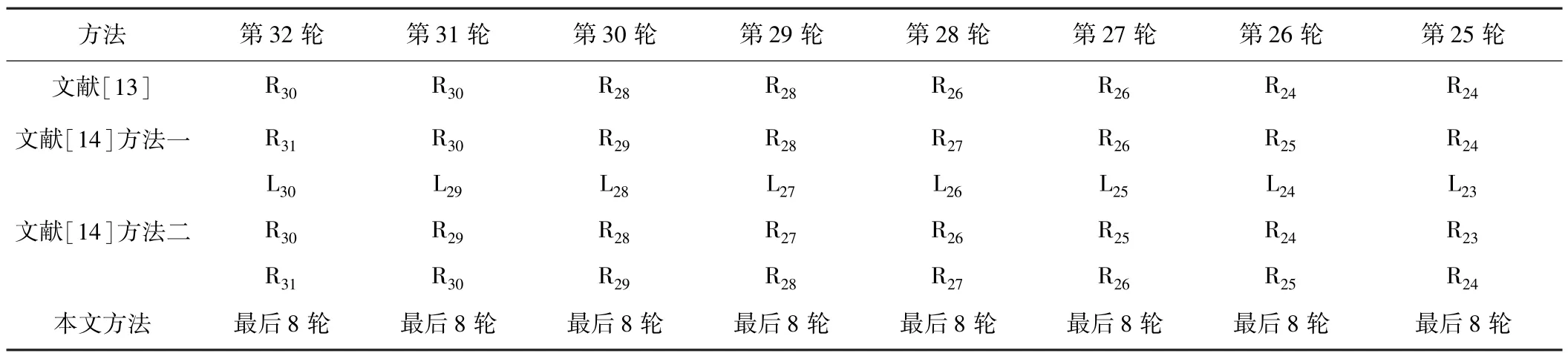
表5 故障诱导位置
5 结束语
进行差分故障分析时常常是在某假设的故障模型的条件下进行,而故障模型的效率不仅取决于需要的错误密文数量,还取决于在实际攻击中的可用性和可行性。针对现有攻击方法的不足提出基于随机故障注入的GOST差分故障攻击方法,将故障诱导的范围扩大到最后八轮,打破了苛刻的理论条件,提高了攻击性和实用性。其次,提出的密钥筛选方法在攻击每一轮子密钥时使用的错误密文都一样,降低了错误密文样本筛选的难度,解决了之前需要根据单轮攻击的具体情况筛选出特定错误密文的难题。本文在一定程度上为同类型密码在实际差分故障攻击中的应用研究提供了新的思路。

