基于元权值学习方法的智能博弈对抗研究

徐志雄 王锋

（陆军边海防学院，陕西 西安710100）

1 引言

近年来，DARPA 发布游戏AI 技术征询启事并资助《星际争霸》游戏AI 研究，美国海军陆战队研发“雅典娜”战争游戏，兰德公司探索人工智能辅助任务规划，从中可以看出，美军正在关注智能博弈对抗技术的发展，为获取未来智能化战争中的决策优势提供理论支撑和技术储备。这对我军发展军事人工智能具有重要的借鉴意义。国内采用智能方法进行指挥决策问题研究也取得很多成果。文献［1］［2］基于模型分析和仿真评估研制了联合作战方案生成与评估系统、空军战役智能决策支持系统。文献［3］～［5］从信息、决策、资源和结构四个方面对方案进行建模，可以对方案执行效果实时跟踪。文献［6］基于多Agent 智能技术和行动方案生成专家系统开发了作战计划协同制定系统。文献［7］研究了制导航弹的任务规划系统，提出了一种任务规划系统的设计方案，但并未对该方案予以实现和验证。文献［8］提出了基于陆军指挥所模型的作战计划独立生成方法，研究了基于大数据的军事情报分析与服务系统体系结构。文献［9］开发了人工智能程序“CASIA-先知v1.0”，利用知识和数据驱动的系统架构，构建了战术团队的智能作战行为模型。

目前，国内大部分研究工作采用有监督或半监督的机器学习方法。然而当前我军缺乏实战数据，且作战装备训练数据数量有限，这一现实条件限制了以深度学习为代表的机器学习方法在作战实体行为建模问题上的进一步应用。相比之下，以强化学习方法为代表的人工智能技术在作战实体博弈行为建模应用方面有了长足发展，为下一步突破作战实体智能决策的“瓶颈”提供了可能。

2 基于加权梯度更新的无模型元深度强化学习方法

2.1 算法设计思路

基于深度强化学习方法的智能博弈对抗是利用以深度强化学习为代表的智能技术，训练出具有认知能力的智能体，可对环境进行感知与认知，利用规则和学到的经验知识，通过与对手的对抗性博弈，实现对最优行为的选择。

作战博弈对抗过程中，基于强化学习方法的指挥作战实体，在参与博弈过程中不断试错，与战场环境持续交互，通过行动探索学习决策经验，从而循环更新自身策略网络来不断调整其作战行动。强化学习训练得到的策略网络，可以理解为作战人员决策经验知识的隐性表达，是指挥决策思维过程的表征。然而，在此过程中还存在诸多难题。传统深度强化学习模型在解决博弈对抗决策问题时，初始策略模型是从随机初始化后的网络上开始训练的，由于复杂战场环境下的状态和动作维度高，采样低效，且训练时作战行动的效果反馈稀疏或反馈不准确，即在采取一定的战术决策后，无法对当前决策进行及时、准确的评价，需要进行到一定阶段后，才会得到一个整体的反馈信息。这导致基于传统深度强化学习方法的初始策略模型的优化存在冷启动问题。针对这一问题，提出基于历史行动轨迹梯度的元深度强化学习方法，通过为初始策略模型提供一种高效的网络初始化办法来解决冷启动问题，提高学习效率和模型性能。

元学习的最新进展为深度强化学习方法提供了一种新的学习方式。通过在任务分布上进行训练，学习元知识，元深度强化学习方法可以凭借很少的交互数据解决新的任务。目前基于梯度的元学习方法不仅在强化学习领域取得了很大成功，而且在监督学习任务上也获得了显著成效。

基于梯度的元学习方法的核心思想是通过利用多个历史行动轨迹中的梯度特征学习来得到网络初始化参数和初始化模型，以便策略模型能够高效地解决新任务［10～15］。然而，目前已经提出的基于梯度的元深度强化学习中普遍存在的问题是，训练得到的初始的基于梯度的网络模型可能会偏向于某些任务，特别是元训练阶段性能较好的一些任务。在这种情况下，最终训练得到的实际上是有偏的基于梯度的网络模型。有偏的初始化模型对新任务的泛化能力差，特别是那些与元训练任务有较大差别的新任务。针对这一问题，本文提出了一种通用的元权值（Meta Weight Learning，MWL）学习方法，通过直接最小化不同任务间的性能差异来训练一个无偏的初始网络模型，使基于梯度的元深度强化学习方法对新的任务有更强的泛化能力，同时提供一种更加高效的网络初始化办法来解决策略模型训练前期冷启动问题，提高学习效率和模型性能。

本文提出的基于元权值学习的无模型元学习算法（Meta Weight Learning based Model-Agnostic Meta-Learning，MWL-MAML）的网络架构是在基于梯度的无模型元学习方法基础上，结合元权值学习机制构建而成。此外，本文还设计了一种端到端的训练方法，来高效地训练权值和网络模型初始化参数。

2.2 无模型元学习算法

本文以无模型元学习（Model-Agnostic Meta-Learning，MAML）［16］为视角，重点研究元深度强化学习的目标。MAML 的目标是在从策略πθ下采集得到的K条轨迹中学习之后找到一个策略πφ，该策略能够最小化新任务分布D（T）上的预期损失。具体来说，MAML 通过使用损失函数的梯度来优化策略πφ的参数φ：

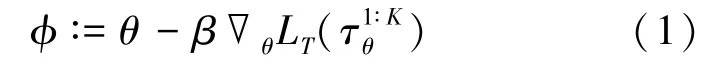
式（1）中，θ，φ分别代表策略πθ、策略πφ的参数，β是元学习率，表示K条轨迹的平均损失函数。

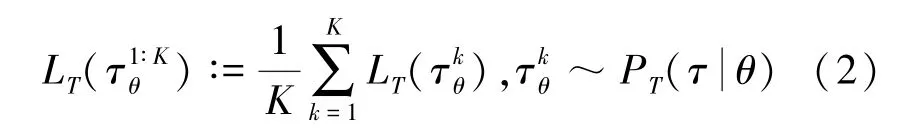
2.3 基于元权值学习的无模型元学习方法

MAML 算法更新目标函数中的平均方法实际上并不能解决策略模型在某些任务上过优化的问题，训练最终得到的仍然是一个有偏的初始化网络模型［17］。

为了解决这一问题，本文提出了一种加权梯度更新机制来最小化初始网络模型对任意给定任务的偏差。

具体来说，给每个轨迹一个梯度更新的权重。为了满足权重归一化的条件，假设第k条轨迹的权重为：

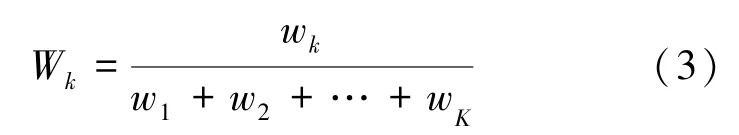
MAML 算法中目标函数更新为：

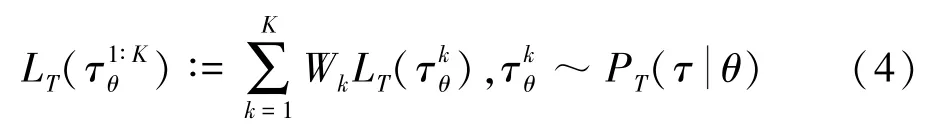
本文通过梯度更新权重代替人工设置权重。权重的更新目标是将w的值设置为在下一次迭代中使目标函数的值最小化的值w*。在上一时间步的权重值基础上执行一个梯度下降步骤，梯度计算为：

因此，下一时刻权值更新估计为：

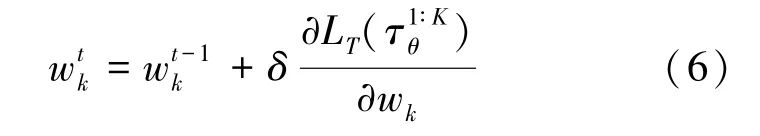
式（6）中，δ是权值w的学习率。需要注意的是，梯度的计算要根据批次测试集上的损失大小，依据更新目标函数来完成。具体地说，由MAML训练的初始网络模型可能偏向于某些任务，并且可能无法有效地解决与元训练任务有很大偏离的新任务，而本文提出的MWL-MAML 算法通过对不同训练任务的轨迹在更新时赋予权值来提高对不同任务的适应性。MAML 和MWL-MAML 算法的更新过程比较如图1 所示。

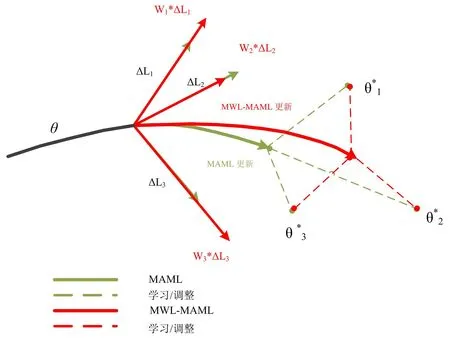
图1 MAML 和MWL-MAML 方法参数更新过程比较

MWL-MAML 的训练思想是对初始网络模型进行无偏训练，通过直接最小化模型在元训练阶段中不同任务上损失的不平衡性，使得元学习器能够学习一个无偏的初始网络模型，而不会在某些特定的任务上产生过优化问题。MWL-MAML 算法的端到端的训练方法见表1。

表1 MWL-MAML 算法流程

MAML 旨在找到对任务变化敏感的模型参数，当模型参数在训练任务的损失梯度方向上改变时，参数的微小变化将对任何从D（T）中采样的任务产生很大的影响，MWL-MAML 的目标就是增强这种模型参数的敏感性，并在参数空间中找到一组参数，使得模型不仅能够适应不同任务，而且能够高效地解决所有任务（使用很少的交互数据）。

本文提出的MWL-MAML 算法只使用了学习过程中采集的轨迹数据，并没有为MAML 算法中引入额外的需要精调的超参数，这确保了提出的方法能够完全基于历史轨迹来自动调整学习方向，一定程度上减少了人工调整带来的不确定性。通过从历史轨迹的梯度特征中最大化提炼知识来调整未来的学习方向，提高学习效率。

3 无人化装备博弈对抗验证

本节选用无人坦克作战行动序列优化问题进行实验测试。以国际公测平台Robocode 为实验平台，分别利用多种基于学习算法的智能坦克（红方）和基于专家系统的规则坦克（蓝方）进行对战，采用2V2 无人坦克对战模式，来验证本文所提方法在博弈对抗任务中的有效性和健壮性。

3.1 对抗场景

Robocode［18～20］是由美国IBM 发布的先进仿真实验平台。在Robocode 中，无人坦克分为3 个部件：机身（Vehicle）、炮塔（Gun）、雷达（Radar）。

仿真对战场景为1 200×1 200 单位像素的2D环境，坦克自身大小为36×45 个单位像素。

Robocode 中一场战斗开始时，每一个机器人都能得到100 个单位能量，在不同的状态下，如撞墙、撞到机器人、打中敌人和被敌人打中时，机器人的能量都会发生改变，而且不同的状态都有不同的能量转换规则。

（1）发射炮弹能量大小：坦克机器人在开始时能以不同的能量发射炮弹，炮弹能量在0.1～3 之间。

（3）当坦克机器人被敌人炮弹打中时：如果敌人炮弹的能量小于等于1，能量损伤度计算公式为4×power；如果敌人炮弹能量大于1，则能量损伤度计算方式为4× power +2×（power-1）。

（4）本文为每回合每辆坦克设置的炮弹数量为100。

每个回合开始时，红蓝双方坦克位置随机分配，双方坦克能量值均为100，若其中一方坦克能量值低于0，则坦克被摧毁，回合结束并重新初始化开始下一轮。

3.2 红蓝对抗智能设计

红蓝无人坦克对抗模式包含了2V2 红蓝坦克协同对战模式。用2V2 坦克协同对战模式来验证基于历史行动轨迹梯度的策略模型优化方法的有效性。采用的学习算法有近端策略优化（PPO）算法、MAML（基于探索的无模型元学习）算法、EMAML 算法以及MWL-MAML 算法。蓝方坦克为一系列基于专家系统的规则坦克的集合，每次对抗时，敌方坦克从集合中随机选取一种规则坦克进行对战，集合中的坦克有Walls 坦克、Fire 坦克、Spinbot 坦克、Crazy 坦克以及JuniorRobot 坦克。坦克对抗设计见表2。

表2 坦克对抗设计

Walls 坦克运动的基本规则是躲藏在战场边缘进行随机移动，雷达对战场进行分区域扫描，一旦扫描到敌方坦克，获取当前帧的敌人位置和自己位置以及射击的角度、子弹的速度，当有足够多的数据后，根据当前的位置和角度，获取最有可能打中敌方的攻击方式。Fire 坦克的对战策略是在对战前期保持车身静止不动，同时雷达和炮管协同转动，转动范围是0～360°，一旦发现目标就采取攻击，发射炮弹，当自身受到攻击时，立刻进行随机移动。Spinbot 坦克的对战策略是始终进行圆周运动，如果运动过程中受到攻击，立即变化圆周运动的方向和半径大小，同时雷达和炮管协同转动，转动范围是0～180°，一旦发现目标立即采取攻击。Crazy 坦克的对战策略是在对战的过程中一直保持高速的随机运动，同时保持机身的加速度时刻处于变化之中，同时雷达和炮管协同转动，发现目标时立即射击。JuniorRobot 坦克的对战策略是保持机身始终以跷跷板的运动方式移动，当它看不到任何敌人坦克时，会保持在机身左右两端旋转雷达，当发现敌方坦克时，立刻转动炮管开火。

3.3 算法参数设置

对于MWL-MAML 方法，超参数的具体设置见表3。

表3 MWL-MAML 方法中超参数设置

此外，PPO，MAML，E-MAML 方法的超参数设置见文献［21］～［23］。

训练和测试时，MWL-MAML 算法坦克、EMAML 算法坦克、MAML 算法坦克、PPO 算法坦克分别与基于专家系统的规则坦克进行对战。每次从集合中随机选取一种规则坦克，每种对战设置为50 000 回合，以100 回合为一个学习周期，共有500个学习周期，每个学习周期结束后记录一次算法坦克得分。每个学习周期结束后，清零双方得分，开始下一个学习周期的得分统计。

3.4 仿真结果分析

根据前面设置的实验场景进行实验。坦克总得分由坦克存活得分和炮弹击中得分相加而来，每一个学习周期记录一次坦克总得分。综合四种算法实验结果，得到四种算法坦克得分结果如图2 所示。

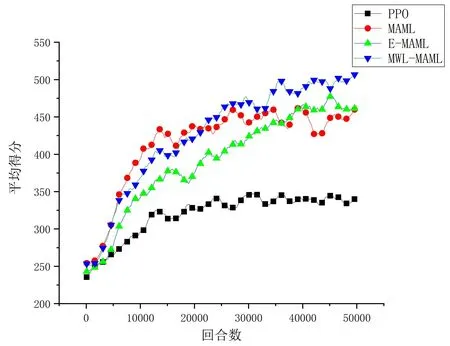
图2 四种算法坦克得分对比

由图2 可知，四种算法中，MWL-MAML 算法的最终平均得分最高。收敛速度方面，MWLMAML 算法和MAML 算法略高于E-MAML 算法，明显快于PPO 算法。表4 记录了四种学习算法收敛后的平均得分和标准差。MWL-MAML 算法相比PPO 算法、MAML 算法、E-MAML 算法而言，平均得分提高了48.7%，14.1%，7.1%；在算法稳定性上，标准差分别减小了22.8%，10.8%，4.5%。可以看出，基于历史行动轨迹梯度的策略模型优化方法有效地提高了基于学习算法坦克对抗策略的胜率，即使在2V2 坦克对战想定中，状态和动作空间维度急剧增大的情况下，仍然能够提升学习效率和算法性能。

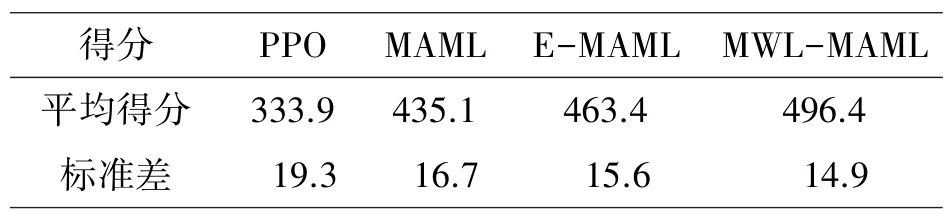
表4 2V2 坦克对战想定下算法平均得分和标准差

图3 为2V2 坦克对战想定下四种学习算法的临界差分图（Critical Difference Diagrams），可以看出，MWL-MAML 的平均得分确实高于其他比较算法。

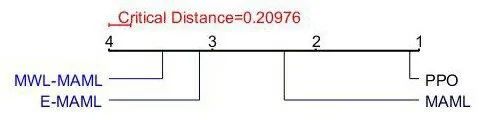
图3 四种学习算法平均得分临界差分图

仿真显示，在红方与蓝方坦克对战时（选取Crazy 坦克作为对手进行测试），红方坦克最终学习得到了两种博弈对抗策略：当红方坦克处于对抗优势时（能量值较高且弹药充足），红方两辆坦克能够迅速针对敌方一辆坦克采取前后夹攻的策略进行攻击；当红方坦克处于对抗弱势时（能量值较低或弹药缺乏），红方两辆坦克能够主动找到战场边缘处进行防守，同时雷达能够分区域扫描，协同防御蓝方坦克。

综合以上实验结果表明，基于历史行动轨迹梯度的策略模型优化方法进一步提高了深度强化学习方法的健壮性和学习效率。该方法对优化无人坦克博弈对抗策略具有重要作用，坦克作战能力得到有效提升。

4 结束语

本文提出了一种基于元权值学习的无模型元学习算法，用少量交互数据就能高效训练新任务，提升对新任务的泛化能力。同时，引入了端到端的训练方法，直接通过从多个历史行动轨迹的梯度特征，来学习训练初始网络参数，优化初始策略模型，解决模型训练存在的冷启动问题。实验结果表明，该算法提升了模型前期采样效率，缩短了训练时长，同时提升了模型最终性能。