高三数学复习课应如何开展解题教学
——以“函数值域的求法”为例
危志刚 (福建省福州第一中学 350108)
解题教学的质量直接关系到高三复习的效果.解题教学看似简单,实则对教师的教学水平是一个很大的考验.好的解题教学不只是分析解题思路,呈现解题过程,最重要的是探索解题方法、揭示解题规律、承载解题思想.本文以“函数值域的求法”为例,探讨高三复习课中如何开展解题教学.
1 从简单的做起
波利亚有一句至理名言:“从最简单的做起”,这特别适用于解题教学.尽管是复习课,教学也必须做到低起点.教学经验丰富的教师都清楚:一个复杂的数学问题解决不了,多半是因为比复杂问题更简单的问题没有理解好;如果简单的问题理解好了,复杂问题的难度就会大幅度下降,甚至可以做到迎刃而解.大道至简,老子在《道德经》中说:道生一,一生二,二生三,三生万物.一个好的简单问题,就是解题教学中的“道”,在解题教学中承担着引导教学、传递数学思想、揭示规律方法的角色.只要我们深刻理解好这个“道”,就可以做到举一反三、触类旁通.

分析1本题为分式型函数值域问题,分子、分母中均含有自变量x,在x变化过程中,分子及分母均随之而变,分式的值的变化不易把握.为了弄清应变量y随x的变化特点,可以考虑分离常数,使得分式中只有分母含有自变量x,分子变成常数,这样可以非常直观地发现y的变化规律,从而求得y的取值集合.因此,采用分离常数法的目的是为了揭示函数的单调性,由单调性分析函数的值域.



分析3从函数的结构特征出发联想几何意义,函数y的结构特点可以对应几何中两点的斜率公式,可以非常直观地得到函数y的值域.这种数形结合的思维方式在解题教学中非常重要,体现了代数与几何的完美融合.

图1
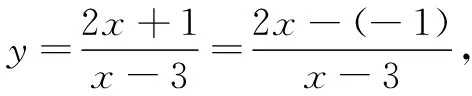
评析引例作为一个简单问题,学生普遍都能作出正确解答.然而,对引例中给出的三种解答的真正数学内涵,多数学生的认知并不清晰.从简单问题出发,由浅入深,揭示解法背后的思想内涵,有利于学生理解解法的数学本质,发挥简单问题在解题教学中的示范性和启发性.
2 形成初步技能
解题技能的形成是一个阶梯式的、逐步发展的过程,需要经历模仿和实践两个阶段.波利亚说过:“解题是一种实践性的技能,就像游泳、滑雪或弹钢琴一样,只能通过模仿和实践学到它.你想学会游泳,你就必须下水,你想成为解题的能手,你就必须去解题.”前面通过引例的学习,学生对函数的值域问题的求解有了一个基本的认知,模仿的解题意识已经初步形成,此时教学中可以通过变式训练的方式,强化和巩固解题技能.变式训练题的设计很重要,不能简单重复引例的模式,在解题技能形成的初级阶段,“变其形,不变其神”的变式题是最理想的.这种变式题使学生“跳一跳够得着”,对于帮助其探索发现解题的一般规律是十分有利的.
评析变式1和变式2的设计符合学生的认知规律,从学生认知的最近发展区着手.如果分别把2x,x2+2x看成一个整体变量,则变式1、变式2的结构与引例的结构完全类似.如果学生能够通过观察发现变式与引例之间的这种共性特征,得到和引例相对应的三种解法也就十分自然了.
3 做到灵活变通
《易经》中有这样一句话:“易穷则变,变则通,通则久”,意思是说生活中一件事情发展到了极致就需要变化,而这种变化让接下来事物的发展不会受到阻碍.这句话折射到数学的解题教学中同样是这个道理,解题教学一定要做到灵活变通、活学活用.我们可以通过不断变化试题的结构、改变试题的条件、转换试题的问法等策略,让试题变得焕然一新,却又让人感觉似曾相识.当然,改变试题的面貌,抛给学生长着新面孔的试题,主要是为学生搭建更多思考的空间平台,不断变化的试题可以提升学生分析问题和解决问题的能力.如果只是用相同模式的试题进行反复训练,容易造成学生简单模仿、死记硬背、机械刷题、不求甚解的现象.只有学生掌握了思考问题的思维和方法,面对新的研究对象,懂得如何去分析,如何去思考,他们才能在解题中真正做到灵活变通、游刃有余.

分析1导数是研究函数基本性质的重要数学工具,本题函数的表达式结构并不复杂,可以考虑利用导数的方法求该函数的值域.


x(-∞,1)1(1,3)(3,5)5(5,+∞)y'+0--0+y递增极大值递减递减极小值递增
所以y的极大值为4,y的极小值为20.又因为x从3的左侧趋近于3时,y趋近于-∞;x从3的右侧趋近于3时,y趋近于+∞.所以y∈(-∞,4]∪
[20,+∞).
分析2本题的函数结构仍为分式型,与前面提到的分式型函数结构特点相似,主要不同点在于分子分母的函数的次数不同,分子为二次函数,分母为一次函数.可尝试分离常数法.

评析导数法是研究函数值域的重要方法,本例解法上的变通是一次十分有意义的尝试.试题解法的多样性,恰好体现了知识的积累和方法的沉淀,厚积方能薄发.解法2通过分离常数的思想,把一个陌生的分式型函数转化为一个常数加上一个熟悉的“对勾”函数.我们仅需研究该“对勾”函数的值域即可得到原函数的值域.解答中对其中的一次结构进行整体化,体现了换元简化函数的思维策略.
4 重视迁移能力
迁移能力,简单说就是一种学习对另一种学习产生的影响,其实质就是将所学到的知识和方法应用到新情境中所表现出来的一种素养和能力.多数学生在面对具有新情境的问题时,往往无法与所学的知识和方法建立联系,这就是典型的迁移能力薄弱的表现.迁移,就是洞悉本质的过程.提升学生的迁移能力,是课堂教学的重要环节和核心任务.解题教学最重要的是思维的教学,不能禁锢学生的思维,只有开放、包容、发散的思维环境才能塑造出强大的迁移能力.因此,解题教学中,要注重新情境的探究、解法的多样性、问题设置的开放性、课堂的动态生成、让学生多发表见解等教学策略的运用.
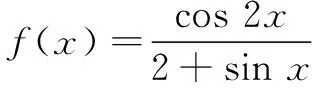
分析分析函数结构可以发现,本题本质上与变式2一致,同为分式型函数,分母可看成关于 sinx的一次型;由于cos 2x=1-2sin2x,分子为关于sinx的二次型.可以通过换元的策略转化为上面已经探讨过的问题,用类似的办法进行解答.


分析1关注到本题可通过三角恒等变换化为关于sinx或cosx的分式二次齐次结构,然后再次利用三角恒等变换中的“弦化切”思想,把函数f(x)转化为关于tanx的分式型函数,然后通过整体换元的办法转化为前面已经研究过的问题,利用分离常数法解答本题.



分析2本题也可通过三角恒等变换化为关于sin 2x或cos 2x的分式一次结构,然后对分式结构进行整式化处理,利用三角函数有界性来解答.

分析3本题的函数为周期函数,把求定义域上的值域转化为求函数在一个周期内的值域即可,可以利用导数法解答本题.
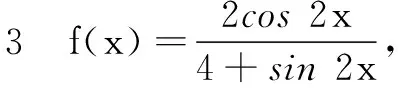


x0(0,α)α(α,β)β(β,π)πy'-0+0-y递减极小值递增极大值递减

分析4本题的函数结构经三角恒等变换后,同样可以利用几何意义的方法进行解答.

图2


评析这两道题的函数“体貌特征”发生明显变化,然而数学本质并未改变.通过简单的恒等变形、换元等手段,可以发现这两题与前面问题的共性.因此,完全可以把解答前面问题的思想方法迁移过来,说明两种方法异曲同工,同根同源.
5 强化选择意识
一道好的数学试题蕴含着丰富的数学知识,承载着大量的数学信息,这种题目的解法通常都比较多.那么,在解题教学中,是不是讲授的解法越多越好呢?其实不然,有些解法是低效的,有些解法技巧性高,有些解法特别繁琐,诸如此类的解法讲多了反而无益,有时甚至会干扰学生对问题的正常理解,容易造成“走火入魔”、误入歧途的境地.那么什么样的解法才是好的解法,我们又该如何选择?首先,能够揭示一般规律、具有普及性的解法一定是好的解法,比如本文研究分式型函数值域中提到的分离常数法,其数学本质实质上是揭示函数的单调性,由单调性研究函数的值域显然具有一般性和普遍性.其次,能够化繁为简、凸显思维的解法一定是好的解法,比如本文中利用几何意义分析函数值域的方法,把繁杂的代数推演简化为简单的几何直观,凸显了数形结合的重要思维方法.总之,好的解法耐人寻味,发人深思.因此在解题教学中,教师一定要有选择地讲解方法,有意识地加强各种解法之间的对比,并给出科学的评价和选择意见.
6 结束语
“格物致知”是中国古代儒家思想中的一个重要概念,意思是探究事物的原理,从中获得智慧或从中感悟到某种心得.高三的解题教学也应该是这样,一节课解多少道题并不重要,通过对试题的分析和解读,探究其蕴含的数学思想方法,揭示其内在的一般性规律,传播智慧,形成能力才是解题教学的真正要义所在.

