以深度参与促进深度学习
范立军



[摘 要]参与是衡量课堂教学有效性的标准,也是开展深度学习的必由路径。以“分数的意义”为例,从教材资源、学生立场和学习经历这三个维度来挖掘引发学生深度参与的因子。从一节课的各个环节入手,阐述认知参与、思维参与和情感参与的策略和方法。
[关键词]深度参与;深度学习;分数的意义
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2022)26-0015-04
教师引导学生参与课堂的过程,是学生理解数学知识的过程,也是学生主动建构数学知识的过程。周玉仁教授认为,要为学生创造多一点思考的情境,多一点思考的时间,多一点活动的余地,多一点表现自己的机会,多一点体会成功的愉快。这些“多一点”确保了学生深度参与的机会,体现了“学为中心”的理念,也为深度学习预留了时空。那么,具体应该如何让学生在深度参与的过程中实现深度学习呢?下面笔者就以“分数的意义”一课为例,浅谈一下自己的做法。
一、透视教材资源,挖掘深度参与的空间
“分数的意义”是人教版教材五年级下册第四单元的内容。教材编写简洁明了,如何挖掘学生深度参与的空间呢?
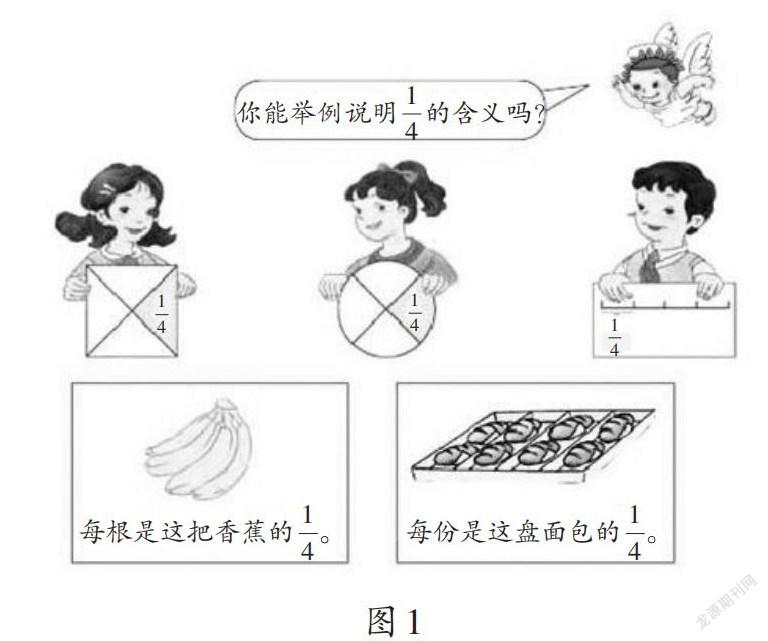
先来看主题图(如图1)。教材利用“你能举例说明[14]的含义吗?”这一提问来引导学生回顾分数的知识,从而引出“把一些物体看作一个整体”这一新知。这一提问确实能让学生参与到课堂中,但只让说明[14]的含义就显得比较单调了。如果让全体学生通过“画一画”的方式来说明一些分数的含义,则不仅可以丰富所要描述的对象,还可以让全体学生都参与到这个过程中来。
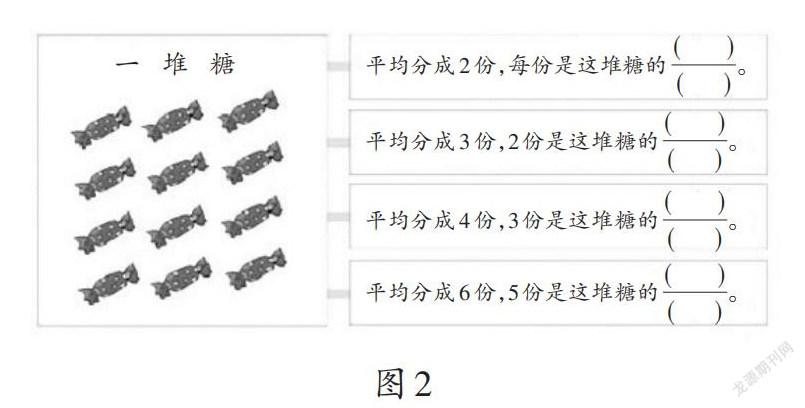
再来看“做一做”(如图2)。这道填空练习题,既是对描述分数的意义的巩固,又为分数单位的教学提供了具体实例,对学习能力较弱的学生来说还是有一定难度的。如何让每个学生都能参与到这个活动中,使分数单位的引出水到渠成?显然,在对这道习题的改造中蕴含着丰富的契机。
通过对各版本教材的分析,笔者发现,现行教材中都没有“把单位‘1’平均分成若干份,表示这样的一份或几份的数叫作分数”这样的定义概括。这就给教学创造了更大的空间,学生可以腾出更多的时间去理解单位“1”,从而感知具体分数的产生过程。
二、立足学生视角,激发深度参与的兴趣
学生在三年级的时候已经学习了“分数的初步认识”,借助操作、直观的方式认识了分数,对在一个物体的基础上产生的分数也已经非常熟悉了。教材中也展示了把多个物体平均分并产生分数的例子,只是没有介绍单位“1”的概念。
把握学生的认知起点,选择合适的素材,创设具有挑战性的问题情境是激发学生参与兴趣的关键。于是,基于上述了解,笔者让学生通过动手实践、合理猜想、对话交流等理解和掌握分数的意义。这既符合学生的年龄特点,又与课程改革倡导的自主、合作和探究的学习方式相吻合。
三、聚焦课堂现场,探寻深度参与的路径
1.认知参与:从“教师提供”到“学生自创”
【片段一】
师:同学们,在三年级的时候我们已经学习过分数了。待会儿我们进行一个叫“想、画、猜”的活动,就是先想一个分数,然后通过一幅图把它画出来,最后让同桌猜一猜你画的是哪一个分数。
【思考】笔者设置这个复习和回顾的环节,一方面是想唤醒全体学生脑海中尘封已久的分数知识,另一方面是想在践行由学生自己提供学习材料这一理念的同时,找到典型的把多个物体看作单位“1”的材料,为接下去的学习活动奠定基础。这样一个操作过程让全体学生调动原有的认知,既复习又引新,充分体现了学生的主体性。
【片段二】
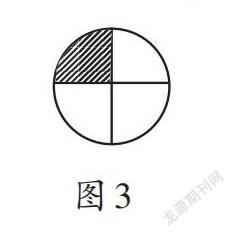
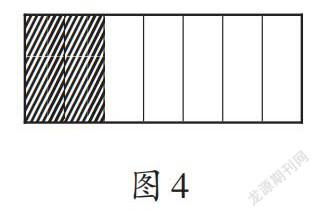
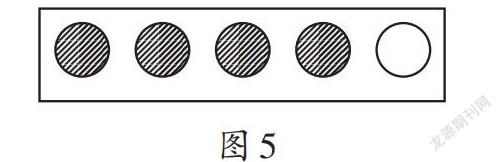
师:老师发现大家刚才都画得很好,猜得也不错。老师收集了几位同学的作品(如图3、图4、图5),让我们一起来猜猜他们画的是哪个分数。
师:你觉得这三幅图哪一幅比较特别?为什么?
生1:图5,因为图3、图4都只包含一个图形,而图5是由几个图形组成的。
生2:我也觉得图5比较特别,因为图3、圖4表示分数的方法我们三年级的时候就学过了,而图5这种表示分数的方法我们还没学过。
师:有道理。图3、图4是把一个图形平均分,而图5是把五个图形平均分。在数学上,一个或多个图形都可以看作一个整体,这个整体有一个专门的名字,叫作单位“1”。请同桌互相说一说,你画的图中把什么作为单位“1”。
【思考】对学生而言,解读同学的作品是他们对已学习的分数知识的一种重新审视。而对图5的表述,是学生对分数认知的一种拓展。另外,对三幅图进行比较,是单位“1”概念生成的基础,而这一切皆源于学生自己提供的作品。这对提供作品的学生来说是一种肯定,也有助于全体学生感受到“新知不新,新知蕴藏在旧知中”。学生的认知不断被唤醒和提升,认知参与的价值和意义就在这个过程中体现出来了。
2.思维参与:从“表层理解”到“深层建构”
【片段三】
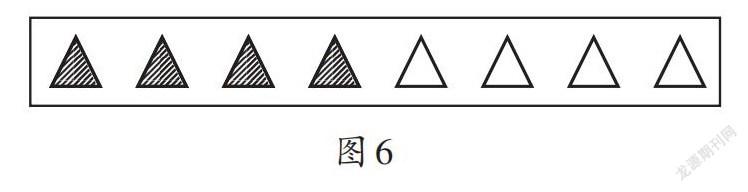
师:这里还有一位同学的作品(如图6),我们一起来看一看。这幅图把什么看作单位“1”?可能表示哪个分数?这个分数是怎么得到的?
生1:这幅图是把8个三角形看作单位“1”,把单位“1”平均分成8份,有阴影的部分占其中的4份,表示的分数是[48]。
生2:这幅图是把8个三角形看作单位“1”,把单位“1”平均分成2份,有阴影的部分占其中的1份,表示的分数是[12]。
生3:这幅图是把8个三角形看作单位“1”,把单位“1”平均分成4份,有阴影的部分占其中的2份,表示的分数是[24]。
师(故作惊讶):同样一幅图却可以表示[48]、[12]和[24]三个分数,这是为什么?
生4:因为平均分的份数不同,阴影部分占的份数也不同,所以表示的分数就不同。
师:从中你获得什么启发?
生5:同一幅图,平均分的份数不同,得到的分数也不同,但这些分数的大小是一样的。
师:说的真好。给这位同学一点掌声!
【思考】对单位“1”的理解是本节课的重点和难点。在这一个环节中,笔者通过展示学生的作品来带领学生理解单位“1”,并拓展把多个图形看作单位“1”时分数的产生过程。笔者在这个过程中只是一个组织者,一切学习活动都是学生自主开展的,材料是从学生的作品中选取的,问题是从学生的思考中提炼的,结论是由学生自己获取的,学生完全站在课堂的中央。观察角度的多样性,表述方式的丰富性,均是思维深度参与的一种表现。
【片段四】
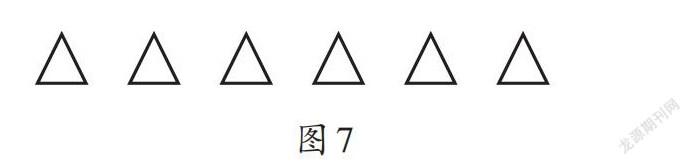
师:老师这里也有一幅没有完成的作品(如图7)。请你们猜一猜,老师这幅图可以表示几分之几?
生1:可以表示从[16]到[66]这几个分数中的一个。
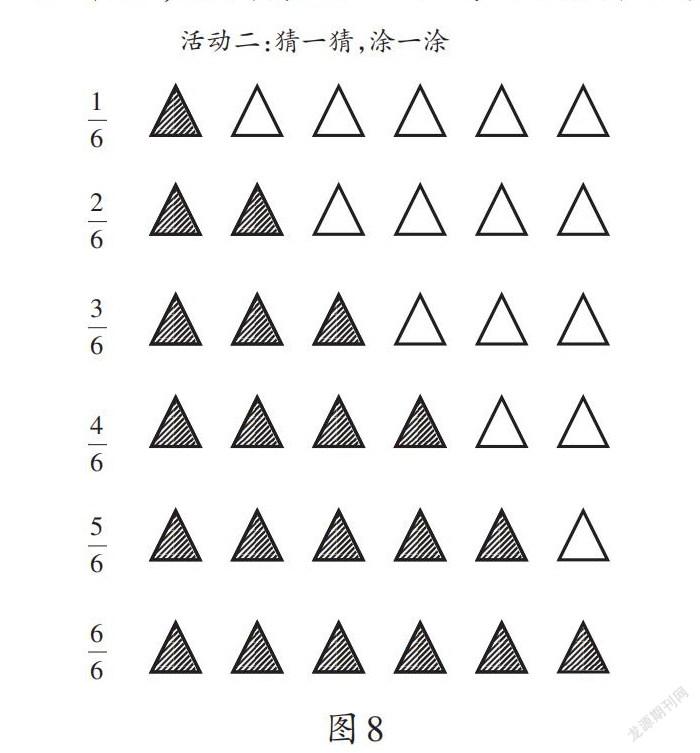
师:请大家在练习纸上画图将这几个分数表示出来,并在旁边写上相应的分数。
(三分钟后,教师展示一位学生的作品)
师:同学们觉得在这幅图可以表示的6个分数中,哪个分数最特殊?为什么?
生2:我觉得[66]最特殊,因为此时6个三角形都画了阴影。
生3:我知道[66]就是1。
师:那[66]里面有几个[16]呢?
生:6个。
师:[16]到[56],各有几个[16]呢?
(生答略)
师:同学们,从刚才的回答中我们可以发现,这些分数都跟哪个分数有关?
生(齐): [16]。
师:是的。像[16]这样的分数在数学上也有一个专门的名字,叫作分数单位。
【思考】分数单位一直是教学“分数的意义”一课的难点,除了直接告诉学生,好像没有什么好的办法。在这个环节中,笔者仍让学生进行操作,使其在不知不觉中感悟到从[16]到[66]的各个分数都是由一个个[16]累积而来的。“数源自于数”的思想在这里无声地进行了渗透,学生也能明白分数单位是组成分数的基础。在这个过程中,教师只是提供了学习素材,整个过程都是以学生已有的知识和活动经验为基础的。
【片段五】
师:现在老师想用这6个三角形表示[14],你觉得该如何表示?注意,这是一幅还没有完成的作品。
师:图9是怎么表示 [14]的?
生1:图9中,把每个三角形平均分成2个小三角形,这样就一共有12个小三角形,在其中3个小三角形中画上阴影,就能表示[14]了。
师:那图10呢?
生2:因为这是一幅还没有完成的作品,所以我擦掉2个三角形,剩下4个三角形,在其中一个三角形中画上阴影,就表示[14]了。
师:从这两幅作品中,你又获得了什么启发?
生3:单位“1”的大小不一样,同一个分数所表示的大小也不一样。
师:说的真好!
【思考】不断生成的挑战性问题在持续刺激学生的思维深度参与的同时,也丰富了学生对单位“1”的内涵的认识。学生思维方式的变通是深度参与之后的产物,也是学生对分数的意义进行深层次理解后的体现。
具体而言,在上述几个教学片段中,能让学生的思维深度参与的条件有两个:一是有可操作性的学习素材,二是有挑战性的学习。这样,学生对单位“1”这一概念的理解就从“表层”进入了“本质”。这也与深度学习基于理解和主动建构的要求相吻合。
3.情感参与:从“冷眼旁观”到“价值认同”
【片段六】
师:关于分数,同学们还想知道什么?
生1:我想知道分数是怎么产生的。
生2:我想知道分数是谁发明的。
生3:我想知道有没有最大或最小的分数。
师:我们一起来看一段与分数有关的视频。
(播放微課:《分数的历史》。最后视频定格在:“一尺之棰,日取其半,万世不竭。——《庄子·天下》”)
师:谁能用分数的知识来解释一下这句古文的意思?
生4:一尺长的棍棒,每日截取它的一半,永远都截不完。
师:看来,你对分数有了非常深刻的认识。
【思考】提出问题不仅是数学研究的重要组成部分,还是数学教学的重要目标。有意义的数学问题的提出也是学生深度参与课堂教学的体现。教学中,教师通过以往的学习经历,以类比思维引导学生提出一个个分数领域的、更有研究价值的问题。通过提问,意犹未尽的学生带着问题观看微课视频,了解更多分数的历史与发展过程,并用自己的语言来解释古文的含义。对于分数的历史,学生不再只是一个看客,他们开始融入自己的期待和理解。这种参与的热情将影响学生往后对分数的学习情感,使迁移应用的可能性在这里得到蕴伏。
综观整节课,学生首先用自己已有的知识经验唤醒对分数知识的记忆,再利用自己创造的学习材料开展对新知的探究,最后通过自主构建,沟通了新知和旧知、经验和方法的联系与区别,彰显了“学为中心”的课堂特征。而教师在这个过程中只是起到“穿针引线”的作用:简要组织、适度点拨、随机小结,尽显“后退”后的从容和闲适。把课堂让给学生,让他们真正体会“我的课堂我做主”的快感。
参与,从大方面来讲是作为一个公民的重要素质,从小方面来讲是衡量一节课是否有效的重要标准。数学学习的过程应是学生主体参与的过程,只有深度参与,学生才能锤炼思维、培育情感,也只有深度参与、提升认知,学生才能对学习内容加深理解,才能主动建构、迁移应用知识,使深度学习在课堂上真正发生。
(责编 吴美玲)

