基于VMD 和WinLSP 相结合的GNSS-R海平面高度估测模型
胡媛,袁鑫泰,刘卫,胡庆松,江志豪,钟李程
( 1. 上海海洋大学 工程学院,上海 201306;2. 上海海事大学 商船学院,上海 201306)
1 引言
海洋对人类社会生存和发展具有重要意义。全球气候变化造成的海平面上升严重威胁到人们的生命和财产安全。因此,观测海平面高度的变化有利于监测自然界的变化,对于海洋学的研究和人类的发展具有重要意义[1]。随着全球导航卫星系统(Global Navigation Satellite Systems,GNSS)的不断发展,GNSS反射(GNSS-Reflectometry,GNSS-R)技术作为一种新兴的卫星遥感技术被广泛应用于海平面测高领域。
相比于传统的测量手段,基于地基GNSS-R 的海平面高度反演技术具有全天候、覆盖面广、时空分辨率高、信号源多和成本低等优势。目前基于地基GNSS-R技术的海平面高度监测方法一般可以分为双天线模式的伪随机码[2–5]、载波相位分析[6–9]方法以及单天线模式的信噪比(Signal to Noise Ratio,SNR)分析法[10–13]。双天线模式指的是GNSS 接收机安装有右旋圆极化(Right-Handed Circular Polarization,RHCP)天线和左旋圆极化(Left-Handed Circular Polarization,LHCP)天线。RHCP 天线和LHCP 天线分别接收卫星直射信号和海平面的反射信号,根据两信号中伪随机码或载波相位的差别进行高度反演。伪随机码测高方法受限于码片宽度,反演精度最低;载波相位分析方法的精度比较好但需要专业的接收机,成本较高不适合大规模应用。SNR 分析法则仅需一根RHCP 天线同时接收直射信号和反射信号,研究两者干涉产生的合成SNR信号进行高度反演。而且,SNR 分析法对粗糙海平面具有更好的鲁棒性。
SNR 分析法的关键之处在于趋势项分离和振荡频率提取,传统模型常采用最小二乘拟合法(Least Squares Fitting,LSF)[14]和LSP(Lomb-Scargle Periodogram)频谱分析法[15]分别进行趋势项分离和振荡频率的提取。LSF 通过最小化误差的平方和寻找数据的最佳函数匹配,一般为低阶多项式。LSF 得到的趋势项存在特定的目标函数与之匹配,这导致其与复杂的SNR 数据进行拟合时存在局限,影响反演精度。同时,由于LSP 频谱分析法在提取振荡频率过程中,会先截断输入信号,然后再进行周期扩展处理,得到一个虚拟的无限信号。但是,SNR 数据不是周期信号,因此这种截断过程会造成频谱能量的泄漏,从而导致误差[16]。
基于上述问题,本文采用瑞典翁萨拉(Onlasa)的GTGU 站2016 年DOY(Day of Year)1-80 和美国阿拉斯加州的SC02 站2021 年DOY 152-211 的GPS 观测数据,构建一种基于变分模态分解(Variational Mode Decomposition, VMD)和凯塞窗函数改进的LSP(记为WinLSP)的GNSS-R 海平面高度估测模型,并利用翁萨拉空间天文台和美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)提供的验潮站数据进行模型精度的验证,该模型可为区域性海平面高度测量提供参考。
2 GNSS-R 海平面高度估测原理
2.1 经典GNSS-R 海平面高度估测模型
SNR 数据分析法进行海平面高度反演只需放置一个RHCP 天线同时接收卫星直射信号和海平面的反射信号。图1 展示了估测模型的几何关系图。
如图1 所示,天线到海平面的反射器高度为h,卫星仰角为θ。根据反射信号相对于直射信号存在的额外的路径和仰角 θ,由几何关系可求得反射器高度h,进而可求得相位差为

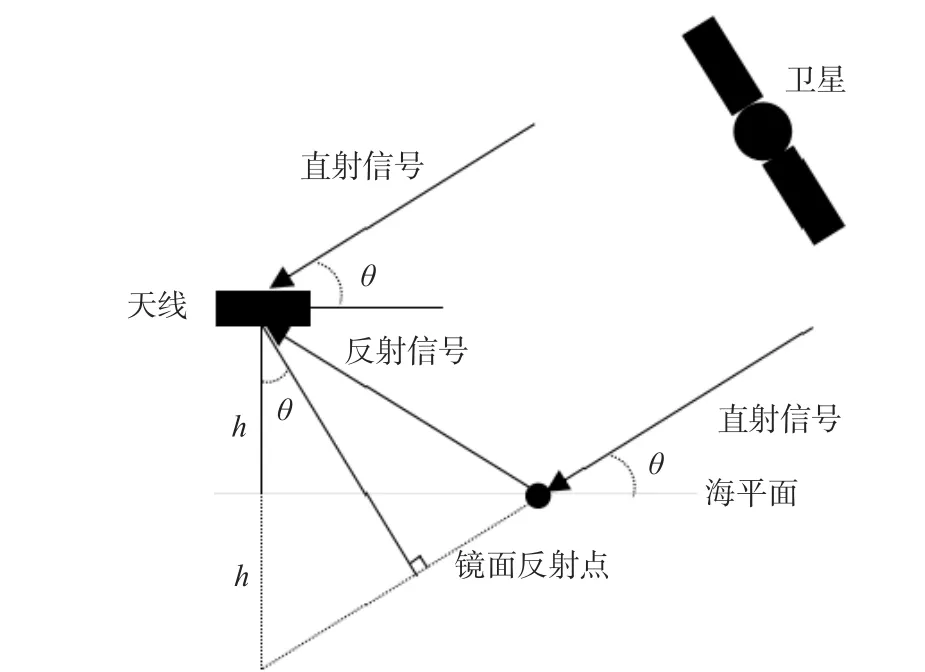
图1 全球导航卫星系统反射(GNSS-R)海平面高度估测模型几何关系图Fig. 1 Global navigation satellite systems-reflectometry(GNSS-R) sea level height estimation model geometric relationship diagram
式中, λ为载波波长。RHCP 天线接收直、反射信号的能量时,对于前者会最大程度的接收。对于后者则表现为抑制,但没能完全抑制。因此,接收机接收到的SNR 信号可以表示为[17]

2.2 变分模态分解理论
VMD 是由Dragomiretskiy 和Zosso[18]提出的自适应、完全非递归的信号分离方法。VMD 通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽,实现原信号的频域剖分和本征模态函数(Intrinsic Mode Function,IMF)分量的分离。此外,VMD 有效地解决了经验模态分解(Empirical Mode Decomposition,EMD)存在的模态混叠、端点效应以及分解层数不可控的问题[19–20]。根据VMD 的分解原理可得[21]:
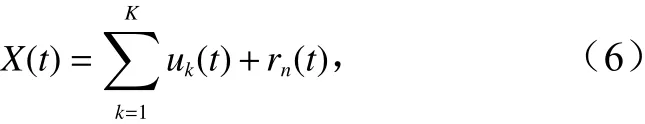
式中,X(t) 表 示输入的原信号;uk(t)表示分解得到的第k个IMF 分量;K表示分解层数;rn(t)表示残差项,一般为噪声。VMD 分解得到的IMF 分量为一个非平稳的调幅调频信号,即

式(2)和式(3)说明了GNSS-R 海平面高度估测模型中需要分离出SNR 数据的趋势项,即干扰项,才能通过频谱分析方法提取振荡频率。针对传统方法信号分离不佳的问题,VMD 能够不局限于特定的表达式,而是基于原始信号本身的特征进行趋势项分离,为估测模型提供更高质量的SNR 数据。为了说明VMD 对SNR 数据趋势项的分离效果,选择了GTGU站2016 年DOY 1 的PRN02 的5°~30°卫星仰角范围的原始SNR 数据进行VMD 分解,如图2 所示。可以明显地看到VMD 有效地将原始SNR 数据分解成具有不同频率的信号。由式(6)可知,VMD 分解得到的IMF 分量频率从高到低排列分别是IMF1-IMF4,同时还有一个残差项。通过比较可以看到IMF4 分量与原始SNR 数据的相关性最高,即为趋势项。GNSS天线实际收集信号时,不仅仅接收卫星的直射信号和经海平面反射的反射信号,同时还接收周围环境产生的噪声信号。这些噪声是非平稳的高斯白噪声,可能会导致频谱分析时提取频率出现误差。VMD 在重构振荡项的同时也减弱了噪声对反演精度的影响。
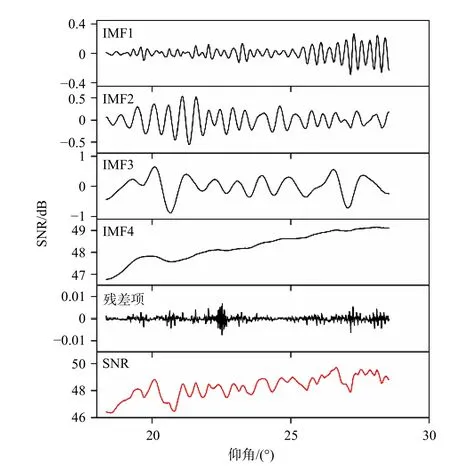
图2 信噪比(SNR)数据的本征模态函数(IMF)分量的组成,从上到下,依次是IMF 分量(频率从高到低)、残差和原始SNR 数据(红线)Fig. 2 Composition of the intrinsic mode function (IMF) component of the signal-to-noise ratio (SNR) data, from top to bottom, followed by IMF components (from high frequency to low frequency), residual and original SNR (red line)
2.3 凯塞窗函数
不同于周期图法和Welch 算法[22],LSP 频谱分析法适用于对非均匀采样的时域信号进行频谱分析。在反演过程中, LSP 频谱分析法在提取非均匀采样的SNR 数据的振荡频率时可能因频谱泄露导致反演误差的增大。窗函数能使时域信号更好地满足频谱分析处理的周期性要求,减少因频谱泄露导致的泄漏,使得所需的振荡频率被更好地提取。窗函数的主瓣宽度和旁瓣幅度分别影响到频谱分析过程中频率的分辨率过滤干扰信号的能力。最理想的窗函数是主瓣宽度最窄,旁瓣最小衰减度最大。但在实际的频谱分析过程中很难找到同时满足这两个要求的窗函数。

3 海平面高度反演实验
3.1 GTGU 站海平面高度反演实验
位于海拔高度40.420 m 的GTGU 站(57.392 954 9°N,11.913 488 6°E)由瑞典查尔姆斯理工大学翁萨拉空间天文台运营。天线的平均垂直位置约为距平均海平面上方4 m,海平面波动约为2 m。如图3 所示,该站点配备了两个Leica GRX1200 接收器和Leica AR 25 天线,可提供时间分辨率为1 s 的GPS 观测数据[25]。为了最大化卫星轨道的数量,GTGU 站天线安装在正南方向。GTGU 站位置避开了海浪,海平面变化主要受潮汐的影响。本实验采用GTGU 站2016 年DOY 1-80 的GPS L1 频段观测数据用于海平面高度反演。为确保SNR 数据来自海平面反射,方位角范围选取70°~210°。距离GTGU 站约1 km 的翁萨拉验潮站每分钟测量一次海平面高度,可用于GNSS-R 海平面高度估测模型精度的验证。

图3 GTGU 站的环境和位置Fig. 3 Environment and location of GTGU station
分离趋势项后,LSP 频谱分析法可用于提取SNR振荡项的振荡频率,并利用下列准则进行有效测高的质量控制:
(1)LSP 频谱的最大幅度高于 20 V(1 s 的采样数据);
(2)LSP 频谱的最大幅度高于2 倍平均背景噪声;
(3)LSP 频谱至少有10 个以上的峰值;
(4)LPS 频谱的最大幅度高于第二峰值幅度的1.5 倍;
(5)有效海平面高度阈值[2, 6]。
3.1.1 基于VMD+LSP 的估测模型精度分析
实验数据选取GTGU 站2016 年 DOY 1-80 的GPS L1 频段信号的SNR 数据。为了验证VMD 在处理SNR数据中的可行性,选取了一段SNR 数据进行VMD与LSF 趋势项拟合效果对比分析,其结果如图4 所示。可以看出基于LSF 得到的拟合结果对于复杂多变的SNR 数据分离效果不佳;而VMD 得到的SNR 趋势项是基于SNR 数据本身进行的拟合,其分离效果较佳而且保留了SNR 数据的局部特征,为接下来LSP 频谱分析提供了质量较高的时域信号。
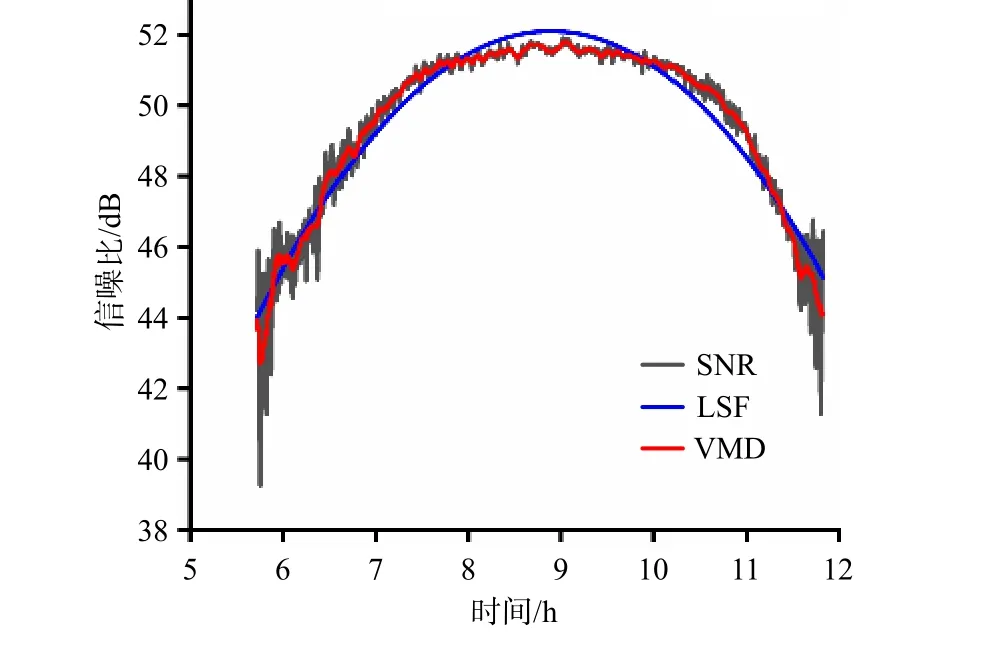
图4 趋势项拟合效果对比Fig. 4 Comparison of the trend term fitting effect
实验期间选取5°~15°、5°~25°和5°~30°不同仰角范围的SNR 数据用于探究低、高仰角对反演结果的影响,实验结果记录在表1 中。从表1 中可以看到,基于VMD+LSP 的GNSS-R 海平面高度反演结果的均方根误差(Root Mean Squared Error,RMSE)约为5 cm,相关系数达到0.98。从结果上看,低仰角范围的反演精度更高,但受限于SNR 数据导致有效的反演点数较少。随着卫星仰角增大,多径信号与直射信号的相干成分越少,干涉效应越不明显,反演结果的RMSE 越来越大,但由于SNR 数据增多得到的有效反演高度也越来越多。因此,5°~30°仰角范围的SNR数据被用于接下来的实验。
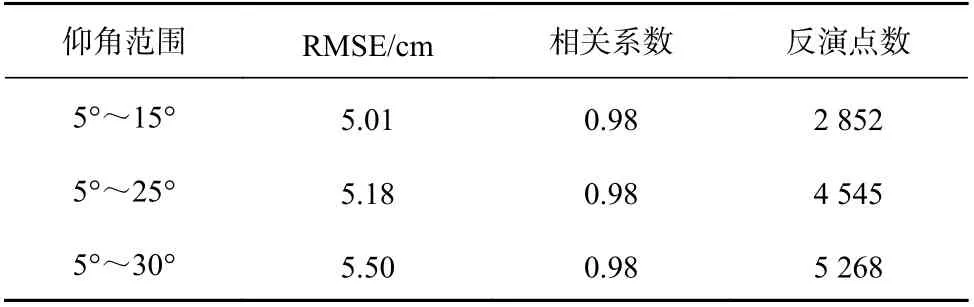
表1 基于变分模态分解(VMD)算法的不同仰角范围的海平面高度反演结果Table 1 Inversion results of sea level height in different elevation angle ranges based on variational mode decomposition (VMD)
在验证基于VMD+LSP 的GNSS-R 海平面高度估测模型精度同时,本文使用LSF+LSP 和EMD+LSP 等模型的反演结果进行精度对比分析,如图5 所示。从图5 可见,不同趋势项拟合方法的反演结果都与验潮站数据高度一致,具体的反演结果记录在表2 中。从表2 中,可以看到基于VMD+LSP 的新模型反演精度最好,其RMSE、相关系数和有效的反演点数分别为5.50 cm、0.98 和5 268,在RMSE 和反演点数上相比于LSF+LSP 的6.69 cm 和4 909 分别提高了约17.8%和7.3%。EMD+LSP 的反演精度次之,其RMSE、相关系数和有效的反演点数分别为5.58 cm、0.97 和4 641,相比于LSF+LSP 在精度也有16.6%的提升,但反演点数则有所减少。总体上,VMD+LSP 的反演精度优于EMD+LSP 和LSF+LSP,这说明VMD 能够更好地拟合SNR 数据的趋势项,分离信号后得到了更高质量的SNR 振荡项用于频谱分析提取振荡频率。

图5 GTGU 站基于不同趋势项拟合方法的反演结果与验潮站数据的对比情况(a)以及海平面高度误差情况(b)Fig. 5 Comparison of inversion results of GTGU Station based on different trend term fitting methods with tide gauge (a)and sea level height error (b)

表2 基于最小二乘拟合+频谱分析(LSF+LSP)、经验模态分解+频谱分析(EMD+LSP)和变分模态分解+频谱分析(VMD+LSP)的GTGU 站海平面高度反演结果的精度对比Table 2 Accuracy comparison of sea level height inversion results of GTGU Station based on least squares fitting+lomb-scargle periodogram (LSF+LSP), empirical mode decomposition+lombscargle periodogram (EMD+LSP) and variational mode decomposition+lomb-scargle periodogram (VMD+LSP)
3.1.2 基于VMD+WinLSP 的估测模型精度分析
本文在构建基于VMD 的GNSS-R 海平面高度估测模型的基础上,利用WinLSP 频谱分析法结合提高海平面高度的反演精度。图6 展示了LSF+WinLSP、EMD+WinLSP 和VMD+WinLSP 的海平面高度反演结果。从图6 中可以看出各模型的反演结果与验潮站数据高度一致,结果记录在表3 中。对比表2 和表3,可以看出不同趋势项拟合方法基于WinLSP 的反演结果的精度相比于LSP 有所提升。从RMSE 上看,加窗前、后基于LSF 的海平面高度反演结果精度提升得最明显,由原本的6.69 cm 减小到5.50 cm,减少了18%。VMD 的提升效果次之,RMSE 减小了15%,由5.50 cm 减少到4.70 cm;而EMD 的RMSE 由5.58 cm减小到5.51 cm,几乎无变化。从得到的有效反演点数上看,WinLSP 相比于LSP 提高了振荡频率提取的精度,使得更多的结果符合质量控制的要求。加窗前、后基于LSF、EMD 和VMD 的反演点数分别增加了11%、17%和7%。在各个组合中,基于 VMD+WinLSP的GNSS-R 海平面高度估测模型的精度最高。相比于传统模型的LSF+LSP,VMD+WinLSP 的反演结果的RMSE 减小了1.99 cm,并且增加了738 点反演点数,即精度和GNSS 数据利用率分别提高了29.7%和15%。
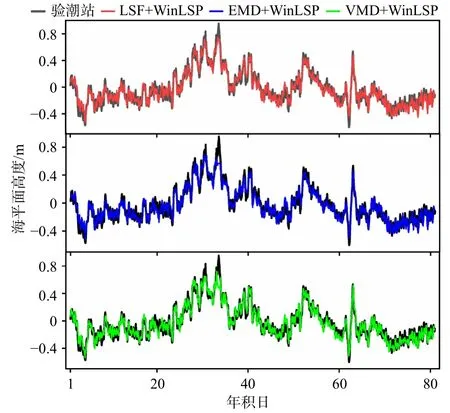
图6 GTGU 站基于加窗的频谱分析(WinLSP)反演结果与验潮站数据的对比情况Fig. 6 Comparison of inversion results based on lomb-scargle periodogram with window (WinLSP) of GTGU Station with tide gauge
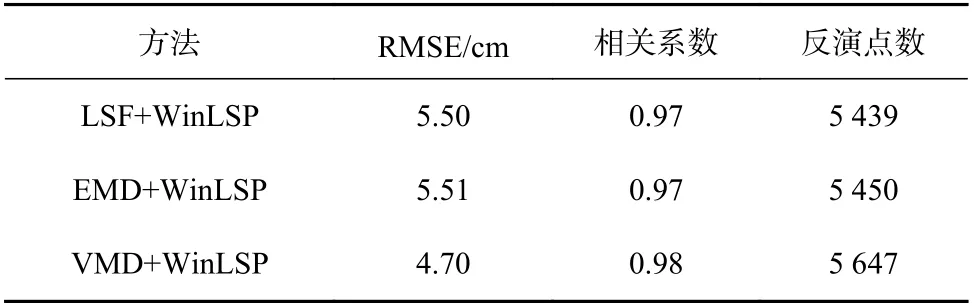
表3 基于最小二乘拟合+加窗的频谱分析(LSF+WinLSP)、经验模态分解+加窗的频谱分析(EMD+WinLSP)和变分模态分解+加窗的频谱分析(VMD+WinLSP)的GTGU 站海平面高度反演结果的精度对比Table 3 Accuracy comparison of sea level height inversion results of GTGU Station based on least squares fitting+lomb-scargle periodogram with window (LSF+WinLSP), empirical mode decomposition+lomb-scargle periodogram with window(EMD+WinLSP) and variational mode decomposition+lombscargle periodogram with window (VMD+WinLSP)
3.2 SC02 站海平面高度反演实验
SC02(48.5°N,123.0°W)站位于美国西海岸的华盛顿州星期五港口,天线的平均垂直位置约在距海平面以上5.5 m,海平面波动约3 m。该测站装置包括一个与Trimble NETRS GPS 接收器相连的Trimble TRM29659.00 天线,以15 s 为一个采样周期记录数据。本文使用了2021 年DOY 152-211 的GPS L1 频段数据开展海平面高度反演实验。为保障SNR 数据来自海平面反射,选取该站的仰角范围为5°~15°,方位角范围为50°~240°。Friday Harbor 验潮站由NOAA运营,位于SC02 站以西约300 m 处并以6 min 的采样间隔记录海平面观测数据。有效高度的质量控制准则与GTGU 站点类似,其中的有效海平面高度阈值改为[2, 9]。
3.2.1 基于VMD+LSP 的估测模型精度分析
与GTGU 站点一致,本文采用LSF、EMD 和VMD 3 种不同的趋势项拟合方法结合LSP 频谱分析法在SC02 站开展海平面高度反演实验,如图7 所示。从图7 中可以观察到SC02 站的海平面波动相比于GTGU 站更剧烈但更加符合潮水涨退的规律。基于LSF+LSP、EMD+LSP 和VMD+LSP 的海平面高度反演结果都取得了不错的反演精度,而且似乎更多的反演结果都集中在低于实验期间平均海平面处。此外,一些离散的反演结果仍然存在,但都在可以接受的范围内。不同方法的反演精度记录在表4 中。不同方法的反演结果的精度没有显著差别,相关系数都达到了0.99,不过可以看到VMD 相比于LSF 和EMD 在RMSE 和反演点数上具有一定的优势。LSF+LSP、EMD+LSP 和VMD+LSP 三 者 的RMSE 分 别 是16.36 cm、15.83 cm 和14.46 cm,反演点数分别是1 632、1 641和1 723。相比于传统的LSF+LSP 估测模型,本文提出的VMD+LSP 在RMSE 上减小了1.9 cm 且增加了91的反演点数,即RMSE 和GNSS 数据的利用率分别提高了11.6%和5.6%。

图7 SC02 站基于不同趋势项拟合方法的反演结果与验潮站数据的对比情况Fig. 7 Comparison of the inversion results of SC02 Station based on different trend term fitting methods with the tide gauge
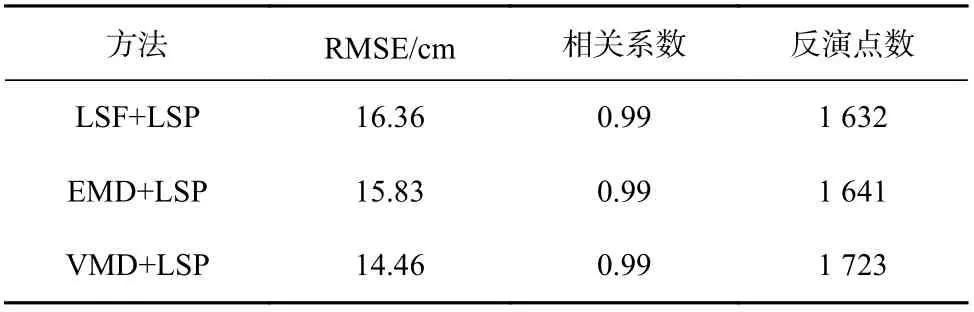
表4 基于最小二乘拟合+频谱分析(LSF+LSP)、经验模态分解+频谱分析(EMD+LSP)和变分模态分解+频谱分析(VMD+LSP)的SC02 站海平面高度反演结果的精度对比Table 4 Accuracy comparison of sea level height inversion results of SC02 Station based on least squares fitting+lomb-scargle periodogram (LSF+LSP), empirical mode decomposition+lombscargle periodogram (EMD+LSP) and variational mode decomposition+lomb-scargle periodogram (VMD+LSP)
3.2.2 基于VMD+WinLSP 的估测模型精度分析
在GTGU 站的海平面高度反演实验的结果表明,WinLSP 频谱分析法提取SNR 振荡项的频率能够减弱因频谱泄露带来的影响,即提高反演精度。为验证提出的WinLSP 方法在不同观测站的可行性,本文在SC02 站开展重复实验。图8 展示了实验期间SC02站基于LSF+WinLSP、EMD+WinLSP 和VMD+WinLSP的海平面高度反演结果。与图7 相似,从图8 中可以看到实验期间平均海平面上、下区域的反演结果并不均匀,大多集中在下半区域。表5 记录了基于WinLSP的估测模型的精度分析结果。对比表5 中不同方法的反演精度,LSF+WinLSP 和EMD+WinLSP 的反演精度十分接近,VMD+WinLSP 的反演精度则较优于前两者。对比表4 和表5,可以看出基于WinLSP 的反演结果的精度相比于LSP 有所提升,而且适用于不同的趋势项拟合方法。从RMSE 上看,加窗前、后LSF的海平面高度反演结果精度提升得最明显,由原本的16.36 cm 减小到15.45 cm,减小了6%,而EMD 和VMD 的提升效果几乎可以忽略不计。从得到的有效反演点数上看,不同方法加窗后反演点数都得到了不同程度的提升。与传统的LSF+LSP 对比发现,最优的VMD+WinLSP 估测模型的反演结果的RMSE 小了2.02 cm,并且增加了153 点反演点数,即精度和GNSS 数据利用率分别提高了约12.3%和9.4%。
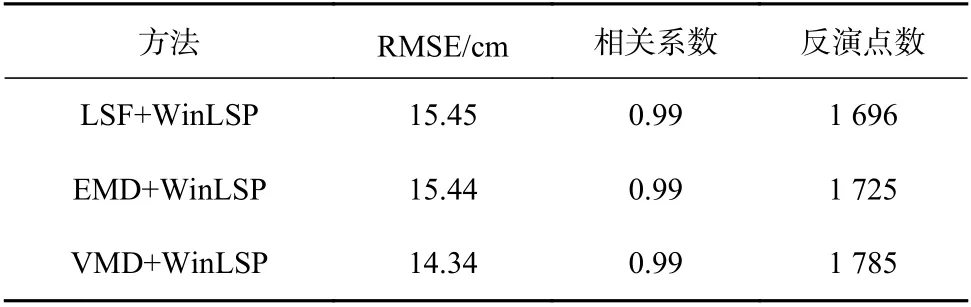
表5 基于最小二乘拟合+加窗的频谱分析(LSF+WinLSP)、经验模态分解+加窗的频谱分析(EMD+WinLSP)和变分模态分解+加窗的频谱分析(VMD+WinLSP)的SC02 站海平面高度反演结果的精度对比Table 5 Accuracy comparison of sea level height inversion results of SC02 Station based on least squares fitting+lomb-scargle periodogram with window (LSF+WinLSP), empirical mode decomposition+lomb-scargle periodogram with window(EMD+WinLSP) and variational mode decomposition+lombscargle periodogram with window (VMD+WinLSP)
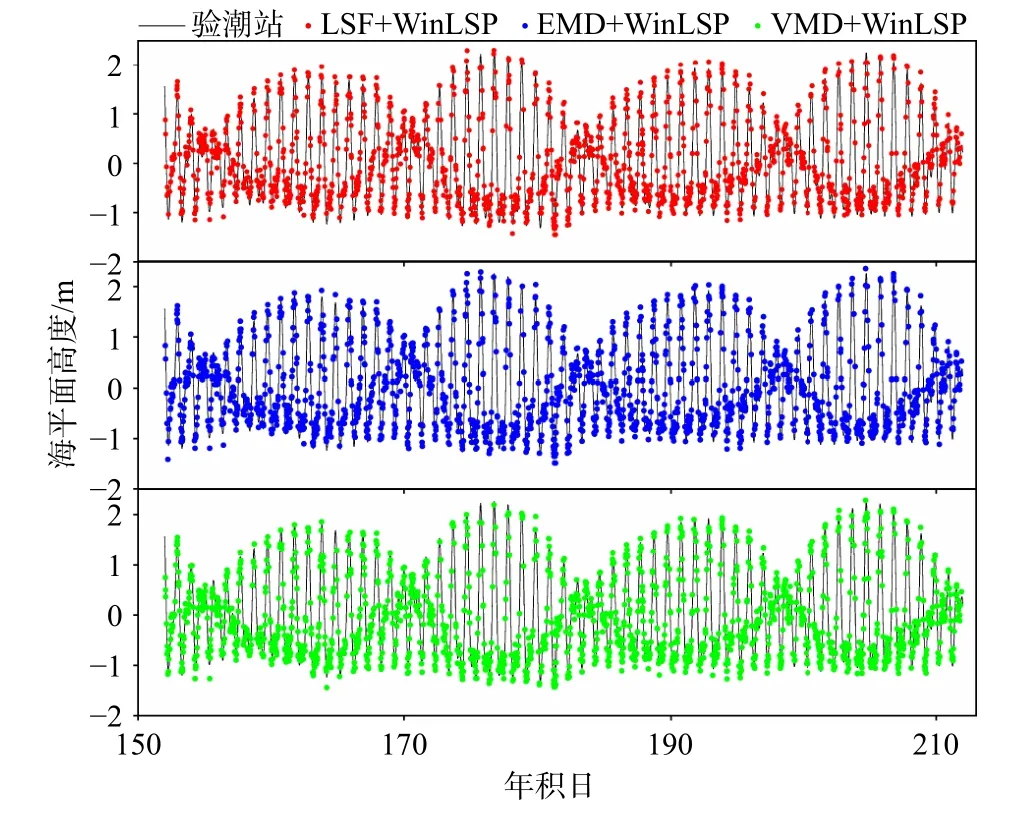
图8 SC02 站基于加窗的频谱分析的反演结果与验潮站数据的对比情况Fig. 8 Comparison of inversion results based on Lomb-Scargle Periodogram with window (WinLSP) of SC02 Station with tide gauge
3.3 讨论与分析
通过在GTGU 站和SC02 站的海平面高度反演实验的结果可见,不同观测站的反演精度以及本文提出的估测模型的提升效果皆存在差异。GTGU 站所处海平面波动较平稳,因此所得反演精度较高可达厘米级。相比而言,SC02 站所观测海平面波动较大,且由于观测位置处于港口处,信号质量受到港口处频繁来往船只的影响。因此反演精度较低,仅为分米级。此外,GTGU 站和SC02 站的采样频率也存在明显的差异,分别为1 s 和15 s。提出的估测模型的精度提升效果是多因素共同影响的结果。
4 结论与展望
高精度、低成本、长时间监测海平面高度变化对于气候学和水资源管理等研究具有重要的现实意义。根据传统的海平面高度估测模型存在的不足,本文构建了VMD 和WinLSP 结合的GNSS-R 海平面高度估测模型,在提高反演精度的同时提高了GNSS 数据的利用率。本文的主要结论如下:
(1)传统的趋势项拟合方法多依赖于最小二乘低阶多项式拟合法,受限于多项式的限制对SNR 数据的拟合效果有效。VMD 对于SNR 数据趋势项的拟合不拘于具体形式,能够根据中心频率的不同对原始数据进行分解,为频谱分析提供更高质量的SNR 振荡项。
(2)传统模型采用LSP 频谱分析法提取SNR 振荡项中的振荡频率时有可能出现频谱泄露的问题,本文引入的基于凯塞窗函数改进的LSP 频谱分析法减小了因频谱泄露导致的误差,提高了反演精度和GNSS数据利用率。
(3)通过在瑞典翁萨拉的GTGU 站和美国阿拉斯加州的SC02 站开展的海平面高度反演实验的结果表明,与传统模型精度相比,本文提出的VMD+WinLSP估测模型在GTGU 站的反演精度和GNSS 数据利用率分别提高了约29.7%和15.0%;在SC02 站的反演精度和GNSS 数据利用率分别提高了约12.3%和9.4%。
综上所述,本文提出的基于VMD+WinLSP 的海平面高度估测模型是可行的,而且提高了反演精度和GNSS 数据的利用率。此外,本文提出的海平面估测模型仍存在一些需要解决的问题,如VMD 最佳分解层数的确定以及估测模型对于其他卫星系统的适用性等。在将来,也许能够结合GNSS 接收机与提出的估测模型构建一套高精度的海平面高度数据产品并推广到全球范围。

