顾及空间自相关特征的机器学习水深反演方法研究

王鑫，贝祎轩，陈卓，张凯,2*

( 1. 山东科技大学 测绘与空间信息学院，山东 青岛 266590；2. 自然资源部第二海洋研究所，浙江 杭州 310012；3. 中兵勘察设计研究院有限公司，北京 100053；4. 广州三海海洋工程勘察设计有限公司，广东 广州 510220)

1 引言

随着我国海洋强国战略的逐步实施，近岸水深数据的需求显著增加。因此，如何高效、准确地获取近岸水深信息成为当前研究热点。目前，水深测量主要依靠船载声呐测量[1–2]与机载激光雷达测量[3–4]。其中，船载多波束测深系统横向覆盖宽度达深度的3～4 倍，可高效获取海底的准确水深信息，但在浅水区效率较低且存在搁浅风险。机载激光雷达测量系统可高效测量浅水区域水深信息，但其广泛应用受到测量成本高和飞行区域合法性的限制。相比之下，利用遥感卫星的多光谱影像反演近岸水深信息[5–6]，因其高效、高时空分辨率、低成本的特点，表现出显著的应用价值。

自20 世纪80 年代Lyzenga[7]提出双层流理论水深反演模型以来，遥感卫星技术的进步有力推动了多光谱遥感影像反演水深理论的发展[8]，所形成的反演方法大致可分为3 类：理论解释模型、半理论半经验模型、统计模型。其中，理论解释模型基于水光场辐射传输方程[7,9–11]，通过建立光学传感器接收到的辐亮度与水深和底质反射的解析表达式来反演水深。这类方法理论严密，但所需水体光学参数较多且获取困难，模型构造复杂。而半理论半经验模型通过结合理论模型和经验参数来实现水深反演，其中以Stumpf对数比值[12]为代表的方法，将辐射亮度表示为深水区与海底反射辐亮度之和，建立其与水深之间的解析表达式来预测水深，得益于模型构造简单与物理机制清晰的优势被广泛应用[13–16]。然而对数比值法特征维度较少，导致反演精度受到模型表达能力的限制[17]。近年来，随着计算机技术的迅速发展，基于机器学习算法的统计模型逐渐成为水深反演最热门的前沿研究领域[18–21]。该方法不需要考虑水深遥感的物理机制，而是从水深与图像辐亮度值之间的统计关系出发，自发学习数据之间的本质联系来建立模型。凭借其在解决多变量、非线性复杂问题等方面的优势，被引入统计水深反演模型中，取得了优于对数比值法的反演效果。然而受卫星影像信噪比低和实测数据量少的制约，多光谱水深反演精度提升有限，成为限制该方法广泛应用的瓶颈。因此，通过深入挖掘数据潜在信息提高水深反演精度，是多光谱水深反演方法研究的一个发展方向。

上述方法通过挖掘影像光谱值与水深之间的函数关系与统计互相关特征进行水深反演。除此之外，水深信息本身的空间统计自相关特征亦可用于估计未采样点位上的水深信息，如基于稀疏水深数据进行空间插值（如反距离加权法[22]、克里金法[23–24]）估计未采样位置的水深信息。因此，在上述传统水深反演方法基础上，通过挖掘水深信息的空间自相关特征，有望有效提高水深反演精度。对此，Su 等[25]提出回归克里金法（Regression Kriging, RK），将空间相关性特征纳入了Stumpf 对数比值模型中，有效提升了水深反演精度。然而，RK 和Stumpf 模型皆属于线性模型，在描述复杂非线性映射关系时表达能力有限。同时，RK 基于平稳假设的前提在实际观测环境中也常常难以得到有效满足[26]。因此，该方法的效果在环境各向异性显著的区域明显下降。

针对上述问题，本文以提高多光谱水深反演精度为目标，利用机器学习在解决多变量与非线性问题方面的优势，通过融合数据源的空间自相关特征与统计互相关性来研究高精度水深反演方法，以期在现有研究基础上，进一步提高预测水深的准确性。

2 方法

2.1 对数比值模型（Stumpf 模型）

对数比值法是代表性的半理论半经验水深反演模型[12]，该方法以蓝、绿波段反射率的对数比值作为反演因子，其模型表达式为

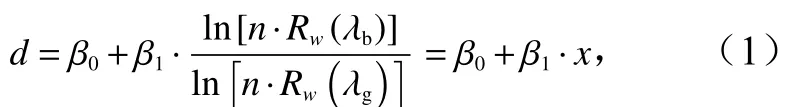
式中，d为反演出的水深；β0和β1是通过回归方程得到的系数；n为缩放比例因子；Rw(λb)和Rw(λg)分别是蓝、绿波段的反射率。

该方法具有构造简单，对环境因素干扰（如大气、水体和海底反射率的变化）不敏感等优势。但作为线性拟合模型，该方法在实际应用中仍然受到复杂水质和海底底质变化的显著影响，难以准确描述复杂海区反射率与水深呈现出的非线性关系[27]。同时，未能综合利用多个波段的光谱测量信息亦是该方法的一个缺点。

2.2 随机森林

机器学习方法可以对不同变量之间的复杂映射机制进行有效学习和表达。其中，随机森林（Random Forest，RF）模型凭借其优秀的非线性回归和泛化能力、多变量特征融合能力以及运算速度快等优势[28–30]，得到广泛应用。用于多光谱反演水深时，RF 模型通过并行处理策略将一组回归决策树组合生成学习器，并利用未抽取样本来泛化模型误差，综合分析每个模型的预测结果。通过上述学习过程，RF 模型可以获得优于对数比值法的水深反演精度，其算法流程如图1 所示。

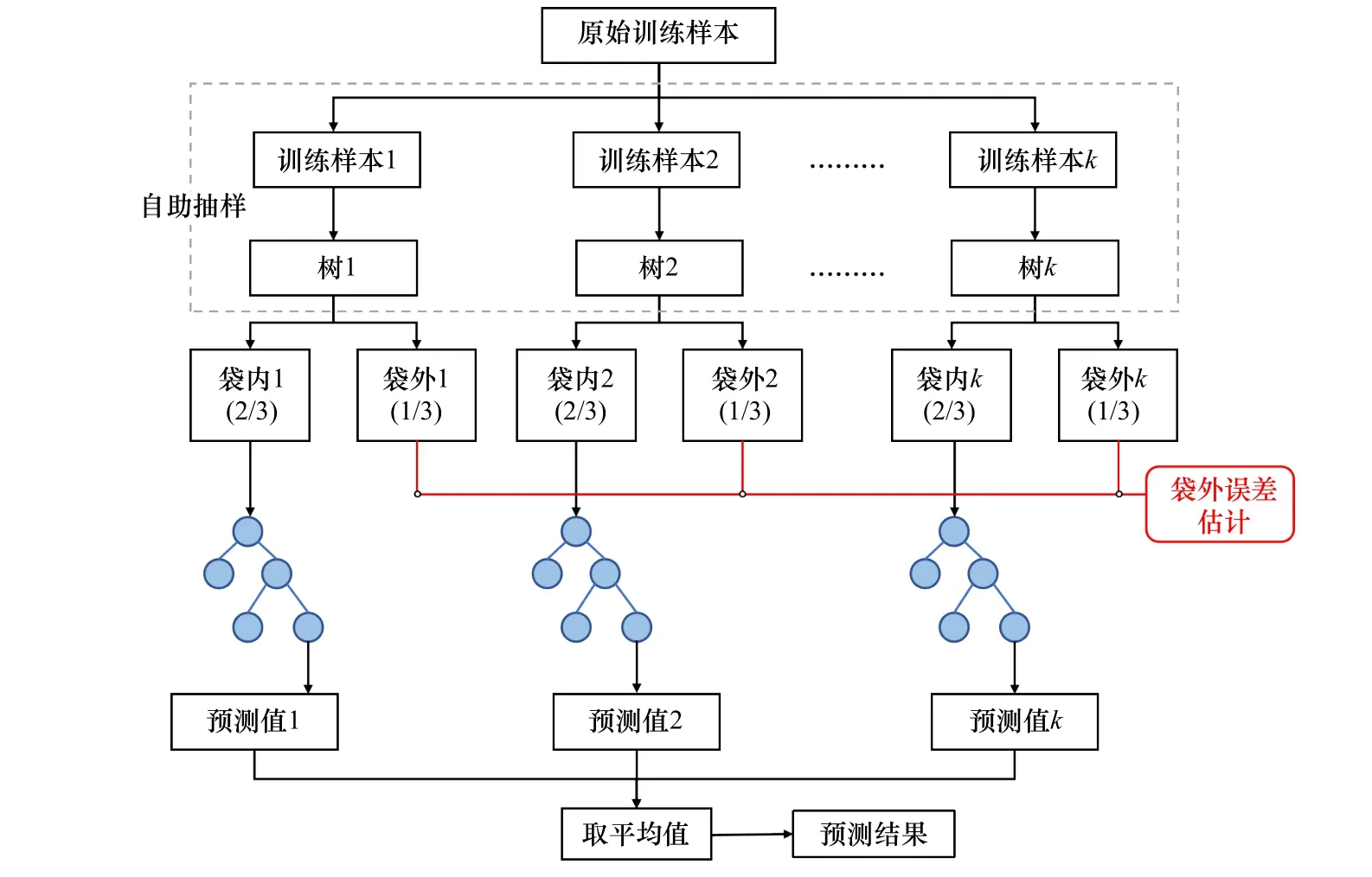
图1 随机森林算法示意图Fig. 1 Schematic diagram of random forest

光学水深遥感反演的物理基础是光对水体的穿透能力，受水体的漫衰减影响，光在水体中的穿透深度与水体特性、不同谱段的漫衰减系数密切相关性，可通过机器学习发掘其中显著而复杂的函数关系。RF 模型的数学表达式为

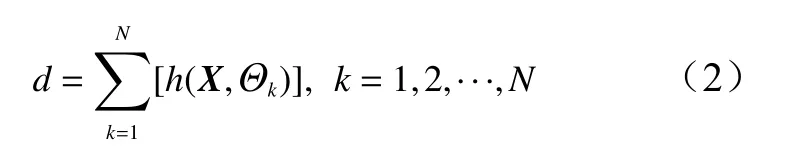
式中，h（ ）代表随机森林算法的函数关系式；N为决策树的总数；输入向量X为波段光谱值；Θk为样本通过模型训练得到的第k棵树的参数向量；d为综合所有决策树预测结果的平均值所得到的反演水深。

2.3 空间自相关随机森林

2.3.1 空间自相关随机森林模型

传统RF 模型通过分析多光谱数据与实测水深数据之间的统计互相关特征预测水深，但忽视了数据自身的空间自相关特征，故未能充分利用有效信息进行学习和表达[31]。为此，本文在训练模型过程中，以实测水深及对应的波段光谱值作为基础因/自变量前提下，将待测点周围具有高度空间自相关性的已知点所对应的属性值作为自相关变量纳入RF 的学习框架中，以此实现统计互相关特征与空间自相关特征的融合。其算法流程图如图2 所示。

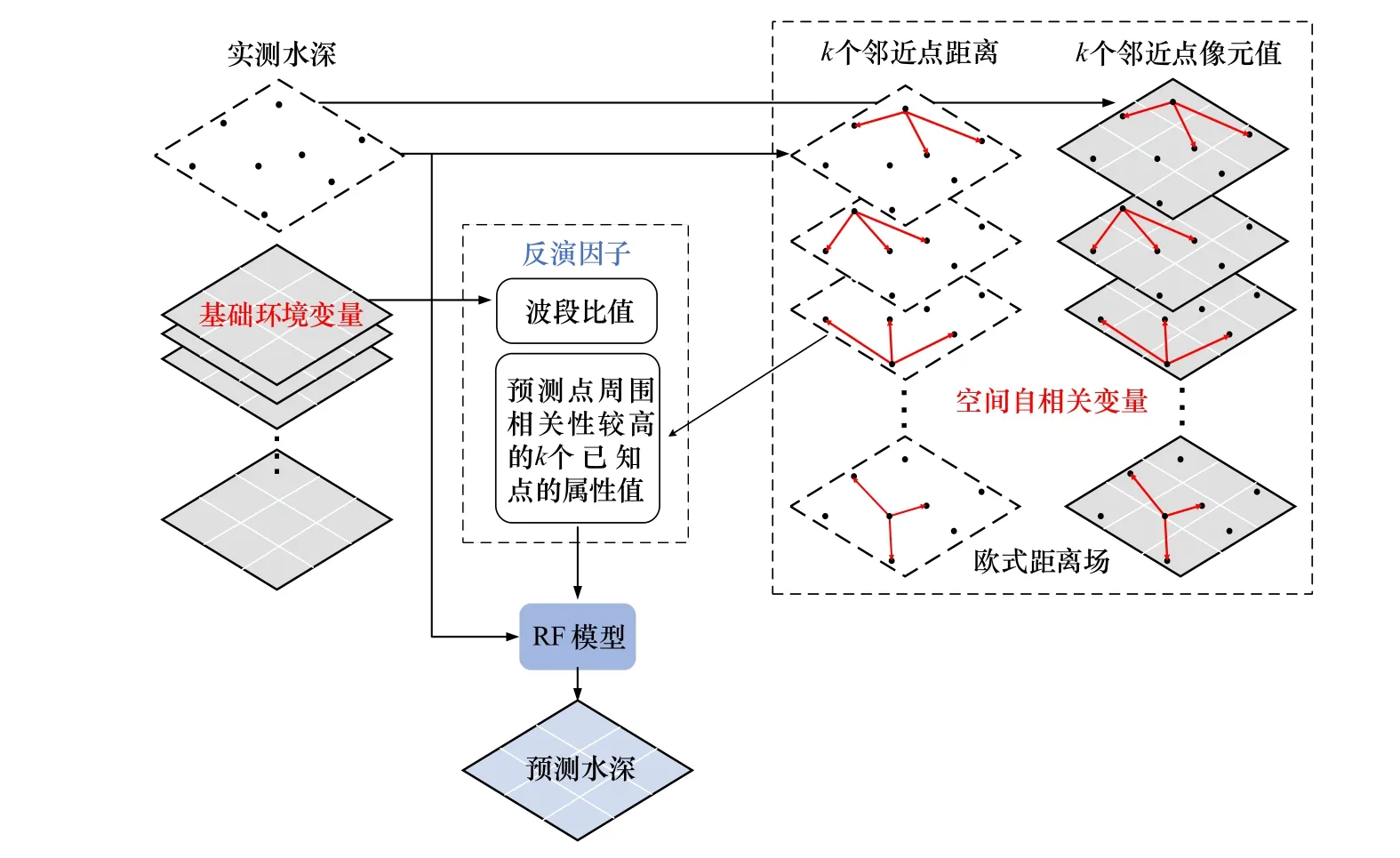
图2 空间自相关随机森林算法示意图Fig. 2 Schematic diagram of spatial autocorrelation random forest

2.3.2 空间自相关与最佳空间间隔

空间自相关特征在遥感图像分析中的应用十分广泛，常用于变化检测与分类优化[32–33]。空间自相关性指的是研究区域内要素的属性值之间潜在的相互依赖性，可用来衡量地理现象空间聚集程度。研究表明，预测点周围具有较高自相关性的已知点所包含的属性信息可用来提高预测的精度[34]，理论上，数据之间的统计相关性越强，预测精度提升幅度越大。对此，全局莫兰指数（Moran’s I）[35]常用于度量研究数据的聚集性于自相关程度。莫兰指数越大，表明研究对象的聚集性越强，自相关程度越高。其计算公式为

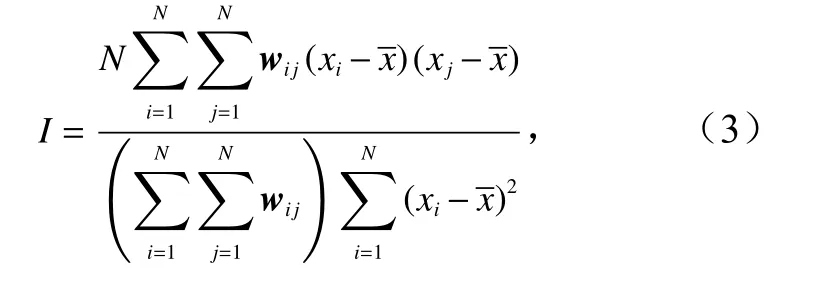
式中，N为要素的总数目；xi和xj分别为第i和第j个要素的光谱值与水深值；x为上述属性值的均值；wij为要素i和j的空间权重值，这里为基于距离的邻接矩阵。

由于Moran’s I 基于空间随机性分布的零假设，因此需要利用Z得分和P值来判断假设是否成立，并检验自相关指数的显著性[36]。其中，P值是由已知分布的曲线得出的面积近似值，而Z值按以下形式计算：

式中，E[I]和V[I]分别为Moran’s I 指数的期望值和方差。

受空间距离的影响，变量的自相关程度仅在一定范围内较为显著，若超过该距离，则认为发生了空间变异。为确定局部最佳自相关的空间间隔，采用半方差来体现空间变异程度[37]，半方差越大，自相关越弱，其计算公式为

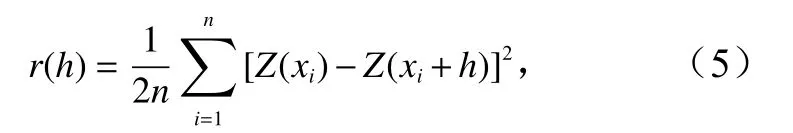
式中，h为样本点之间的距离；n为距离h范围内成对样本点的数量；Z为样本点所对应的不同波段光谱值与水深值。

2.3.3 空间自相关变量

为了获取训练样本的自相关特征信息，需要建立局域子窗进行提取，具体步骤如下：

（1）计算训练样本的水深与不同波段值的半方差函数和莫兰指数，用于确定搜索窗口初始尺寸。

（2）根据计算窗口中待测点到m个已知点的二维欧式距离进行排序，得到衡量自相关程度的距离向量Dn，并将遍历所有待测点得到的n个距离向量，合成为空间自相关距离矩阵（EDF）。

（3）由于训练数据分布的不均匀性，Dn中元素数量k应取所有距离向量的最少元素数目，且需保证不等于0，以满足向量组成矩阵的条件；此外，为在不影响预测精度条件下，提升模型训练效率，还需对搜索窗口大小进行调整并重复步骤（2），将得到的EDF作为表征数据空间自相关特征的补充变量，EDF的具体计算公式计算为

2.3.4 空间自相关随机森林模型训练/验证

基于上述步骤，空间自相关随机森林（Spatial Autocorrelation Random Forest，SARF）模型训练与验证过程存在一定差异，下面列出关键步骤说明。

（1）对水深点个数为a的训练数据而言，所用的水深点既充当待测点，也作为已知点参与模型训练，即按给定的搜索半径计算每个当前水深点到周围邻近点的距离，用以构成大小为a×k的自相关矩阵EDF。将当前点水深值作为监督学习的因变量，与空间自相关变量、基础自变量输入RF 模型中训练，得到训练参数。

（2）对于验证数据（数量为b）来说，每个水深点都为待测点，故需将训练数据中的所有水深点作为已知点来构建自相关矩阵（大小为b×k），并将待测点对应的空间自相关变量与基础自变量输入训练好的模型中，即可求得待测点水深。

3 实验区域与数据源

3.1 实验区域概况

本文研究区域为北岛周边浅海水域。北岛位于南海西沙群岛海域七连屿的中部，面积约为3.6 km2，岛礁呈长条形（图3a）。作为典型的珊瑚岛，其底质由珊瑚、砂和贝屑组成，水下地形特征复杂。由于远离大陆且受人类活动影响小，岛屿周边水质清澈，适合多光谱水深反演。式中，Dn为距离向量；EDF为n个距离向量的集合。

图3 北岛地理位置（a）及原位水深点测量分布（b）Fig. 3 Location of Beidao (a) and distribution of in situ depth measurements (b)

以每个距离向量中k个元素为前提，按其自相关程度的强弱顺序，依次获取每个已知点所对应的属性值并将其与EDF共同组成空间自相关变量X2，与基础变量X1构成反演因子。

式中，r1、r2、r3为预测点对应的蓝、绿、红波段光谱值比值，即Bblue/Bgreen，Bgreen/Bred，Bblue/Bred；r1k、r2k、r3k、zk分别为k个已知点的光谱值比值与水深值。

3.2 数据源

本研究使用的原始影像为高分辨率的World-View-2 卫星影像（图3b），拍摄于2017 年3 月11 日11 时。多光谱分辨率为1.84 m，包含蓝、绿、红以及近红外4 个波段。使用的数据来自于2013 年4 月测量得到的北岛1:2 000 陆域及水下地形测量图，对其进行矢量化与筛选后得到1 700 个水深点（图3b）。

3.3 数据预处理

数据的获取过程中存在时间、空间以及仪器测量带来的误差，因此在利用遥感影像与水深数据进行定量水深研究前需要对这两类数据源进行预处理。对于Worldview-2 影像，首先通过辐射定标和大气校正得到真实地物反射率，并对影像进行几何校正以及云雾和陆地部分的掩膜，使用Hedley 法[38]消除受到太阳光、海面波浪和光线入射角度等因素造成的太阳耀斑。对于水深数据而言，将其坐标转换到与影像同一坐标系UTM WGS-84 下，并进行地理配准，以提取水深点对应的像元值。由于遥感影像采用的是卫星过境时瞬时海面深度，而实测水深数据是以理论深度基准面为基准的稳态水深，因此还需要根据潮位预报表提供的潮高进行潮汐改正。

本文中水深分布区如图4 所示，主要集中于0～6 m浅水区域。为模拟小样本浅海水深反演这一常见应用场景，同时确保数据具有代表性，以1 m 为间隔分层抽样，共选取150 个水深数据作为训练样本，而剩余1 550 个水深点则作为验证样本。为定量比较4 种反演模型效果，本文选取决定系数（R2），均方根误差（RMSE）和平均绝对误差（MAE）进行精度评价。

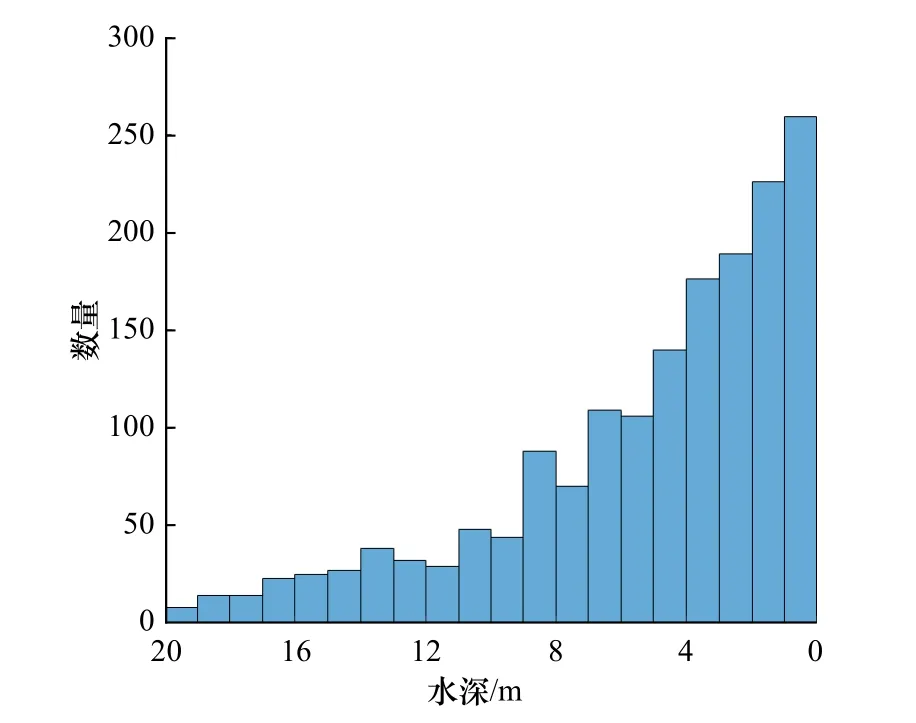
图4 水深点分布区间与数量Fig. 4 Distribution interval and number of water depth points

4 实验结果分析

4.1 变量的空间自相关性

通过计算训练样本的Moran’s I 指数、Z值和P值对水深与波段光谱值的空间自相关性加以评估（表1）。以蓝光波段为例，Moran’s I 指数为0.631，说明该波段光谱值呈现出较强的聚类型式，而其Z值（10.967）和P值（0.001）则表明可以拒绝空间随机性分布的零假设，并通过了置信度为99%的显著性检验。表1 中结果显示，训练数据的水深、蓝、绿波段皆具有显著的自相关性，而红光波段自相关性较弱。

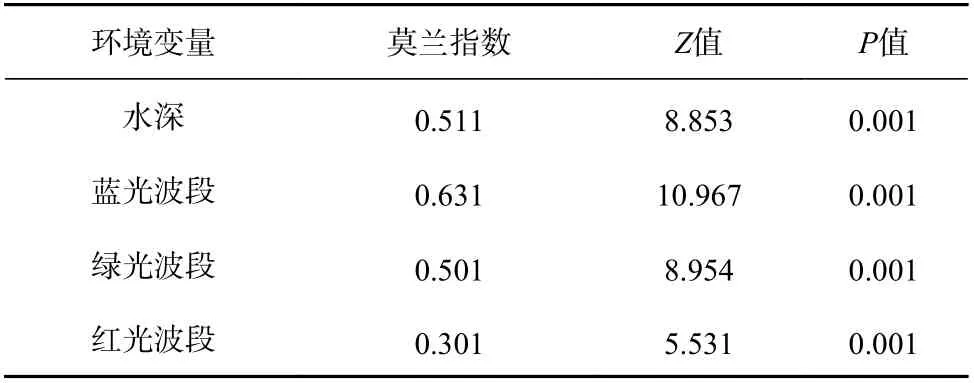
表1 研究区变量的全局莫兰指数、Z 值和P 值Table 1 Global Moran’s I, normalized Z value and P value of variables in the study area

4.2 搜索窗口尺寸确定

研究区域变量的全局Moran’s I 及半方差随空间间隔的变化如图5 所示，通过计算波段值的半方差，并除以最大值归一化后与全局Moran’s I 对比发现，随着空间间隔变大，全局Moran’s I 减小，而半方差值呈上升趋势，这表明变量的空间变异程度增加，而空间自相关性逐渐减小。值得注意的是，二者相交所产生的交点反映了空间自相关与空间变异的平衡。对于水深及蓝、绿、红波段而言，对应的最佳空间间隔分别为175 m、156 m、152 m 和76 m，这表明上述变量在该局域内具有显著空间自相关性。基于上述观察，本文将初始搜索窗口尺寸定为175 m，并根据距离向量的最小元素数原则，将搜索窗口尺寸扩大为220 m，用以获取空间自相关变量并构建SARF 水深反演模型。

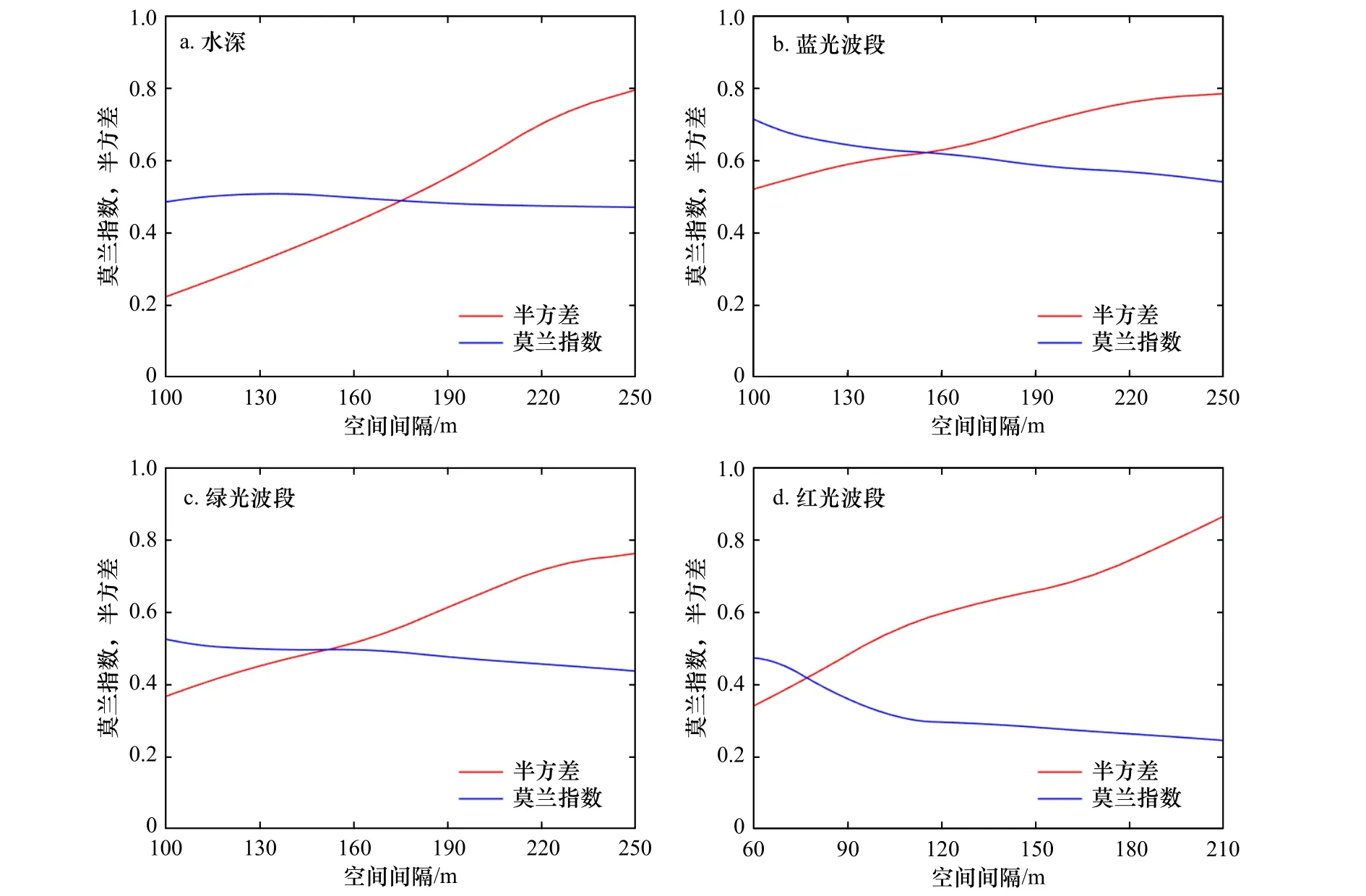
图5 全局的全局莫兰指数及半方差的变化Fig. 5 Global Moran’s I and semivariance with different lags of variable

4.3 精度评价

为验证实验方法效果，本文首先将反演结果与传统方法进行了对比（表2）。可以看到，受限于模型表达能力，Stumpf 模型反演精度最低，RMSE 为2.067 m，R2仅为0.797，相关性也最低。普通克里金（Ordinary Kriging, OK）模型受限于空间插值方法对样本点密度等要求，在小样本实测水深数据集的条件下，其预测精度亦不甚理想（RMSE 为1.894 m）。RF 模型得益于综合多个波段光谱信息，RMSE 为1.635 m，决定系数达到0.888，相比前两种模型预测结果更准确。在这4 种模型中，SARF 模型表现效果最好，RMSE 仅为1.338 m，相对于RF 模型预测精度提升18%，同时相关性参数也提高到0.923。

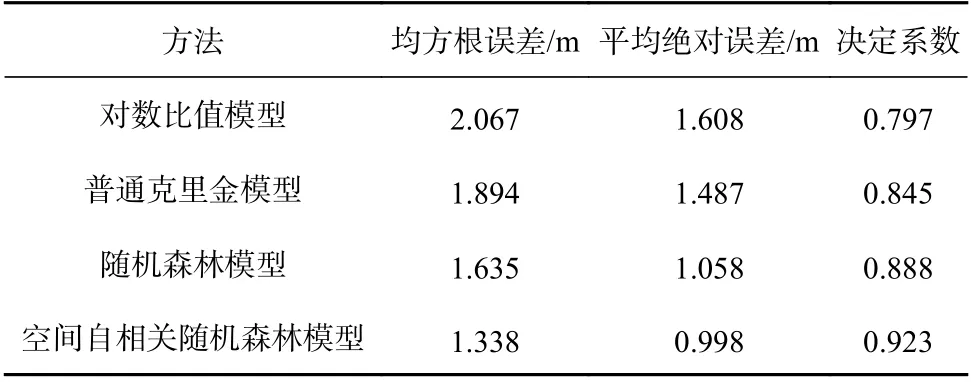
表2 验证数据测试精度对比Table 2 Accuracy comparison of different methods

4.3.1 误差分析

为了比较4 种模型的反演精度和优劣性，根据水深反演图（图6）对不同方法的预测结果与真实水深进行对比分析。图6 中黑线是斜率为1 的指标线，黑线上方表示预测水深值大于实测水深值，下方则表示预测值偏小；红线是通过最小二乘拟合的趋势线，用以衡量与指标线的拟合程度；为体现预测值聚集区间，采用色棒来标识，聚集程度越高，则数值越大且颜色越浅。

Stumpf 模型的水深反演效果如图6a 所示，在水深浅于10 m 的区域，反演结果与实测水深符合较好。但是受限于线性表达方式，出现反演水深值小于0 的不合理情况，且对于深于10 m 的数据，水深反演结果产生了明显的偏差。很显然，该偏差现象产生的根源在于线性模型无法准确拟合数据的非线性特征；类似地，作为非线性局部拟合方法，OK 模型较为准确地预测了0～8 m 区域水深（图6b），而受制于8 m以深实测数据量的减少，无法真实还原深水区情况。虽然该方法顾及了水深的自相关特征信息，但未考虑水深与光谱值之间的相关性，因此只能通过增加实测数据量来弥补模型的缺陷。对比前两种模型，图6c和图6d 中机器学习预测精度提升效果明显，较为完整地还原了研究区域内真实水深分布情况。但从细节上比较发现，RF 模型受训练过程中低信噪比与实测数据量不足影响，指标线上方出现大量离散点且与趋势线相距较远，并影响了预测结果可靠性；与之相比，SARF 模型具有明显的抗离群值效果以及更高的反演精度。

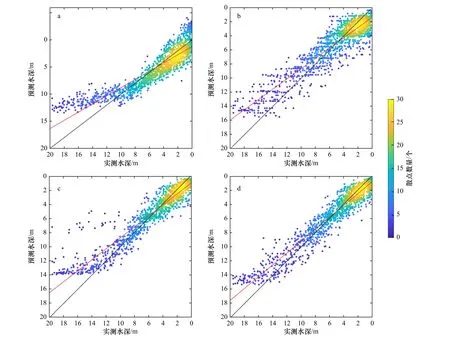
图6 对数比值（a）、普通克里金（b）、随机森林（c）和空间自相关随机森林（d）模型反演水深散点图（训练数量为150）Fig. 6 Scatter diagram of predicted depth values by Stumpf (a), ordinary Kriging (b), random forest (c), and spatial autocorrelation random forest (d) models (the number of training data points is 150)

残差分布图分别给出了不同方法在表达水深-波段值耦合机制过程中的差异，从而通过残差的分布形式来对4 种模型的细节差异进行比较（图7）。图7a显示，Stumpf 模型的残差在10 m 以深区域呈现出明显的递增趋势，预测值与真实值存在较大差异；由图7b 可知，OK 模型整体残差值较大，特别是在8 m 以深区间，大量的离散点明确显示出模型自身的缺陷；而RF 模型在浅水区域的效果较好（图7c），残差值在0 两侧均匀分布，但在水深超过10 m 的区域，其预测结果受到离群值干扰；与前者相比，无论是从残差整体分布形式，亦或是深水区数据受自身统计值波动影响所产生的离群点数量，SARF 模型都表现出更明显的优势（图7d）。

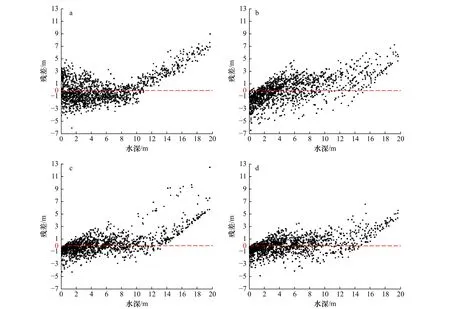
图7 对数比值（a）、普通克里金（b）、随机森林（c）和空间自相关随机森林（d）模型的残差散点图（训练数量为150）Fig. 7 Scatter diagram of residual error by Stumpf (a), ordinary Kriging (b), random forest (c), and spatial autocorrelation random forest(d) models (the number of training data points is 150)

4.3.2 不同训练样本数量下反演结果的精度对比

训练样本数量的变化可显著影响机器学习方法的预测效果。通过计算训练样本数为500 时SARF 模型和RF 模型的残差标准差（图8a）可以看到，RF 模型残差标准差（1.295）远高于SARF 模型（1.012），因此后者残差离散程度较小，分布更为集中；其次，通过观察0.05 显著性水平下残差分布区间发现，RF 模型残差主要分布于[1.25, 1.35]，而SARF 模型残差分布区间集中在[0.97, 1.05]，后者的残差分布幅度更小，说明预测值与实测值拟合效果更好。除此之外，通过观察训练样本占全部样本比例下的均方根误差（图8b）发现，SARF 模型的误差大小及其下降速率始终小于RF 模型，且随着训练数据量的增加，该优势愈加明显；当训练样本占比达到60%时，相比于RF 模型，SARF 模型的误差降低约27%，该结果进一步验证了将数据源的空间自相关特征纳入机器学习框架中，可显著提升预测结果的准确性。

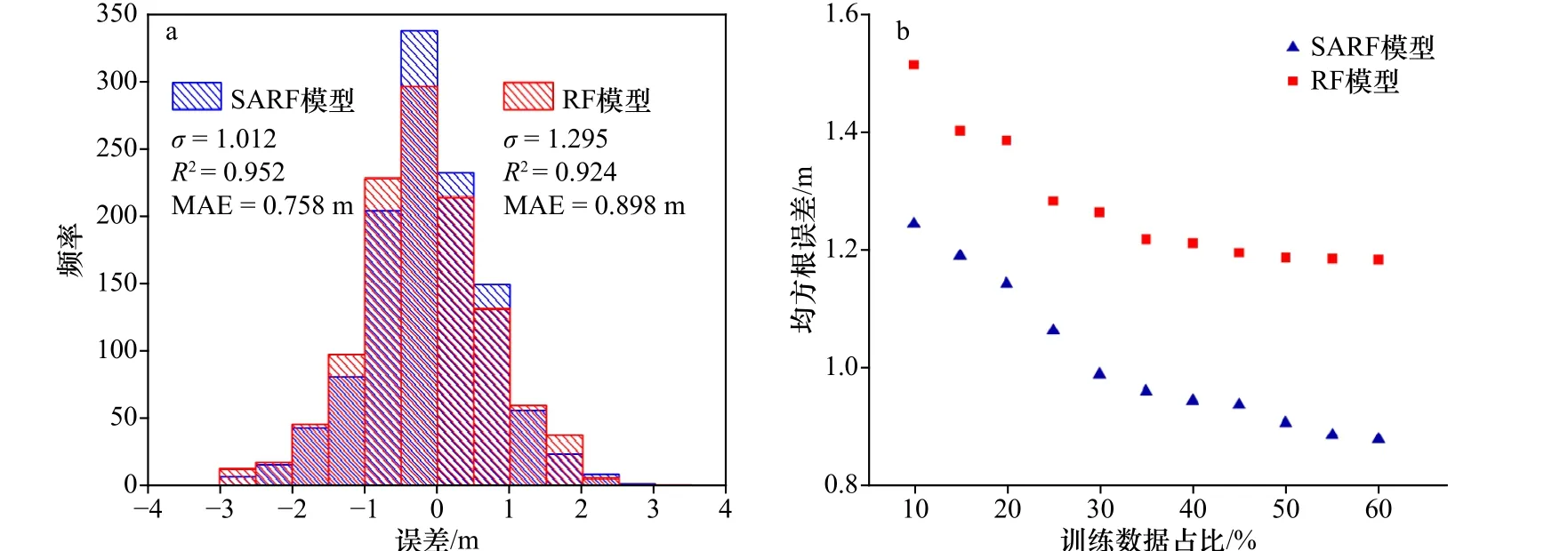
图8 训练样本量500 时残差分布直方图（a）和不同训练数据占比下的均方根误差（b）Fig. 8 The histogram of error distribution when the training sample is 500 (a) and root mean square error for different training data shares (b)

本文基于SARF 模型使用350 个训练数据得到北岛海域反演水深，并将其与实测陆上高程点生成反演水深与陆域地形图（图9a）。可以看到，珊瑚岛周围海底地形分布表现出复杂的特征。近岸浅水区域海底主要由沙质沉积物构成，水深变化较为平衡。而在离岸较远的区域，受海流的影响，岛屿南北两侧呈现出截然不同的海底地貌细节特征（图9b）。显然，海底地形信息表现出较强的空间相关性，从而验证了利用空间相关性辅助水深反演的有效性。

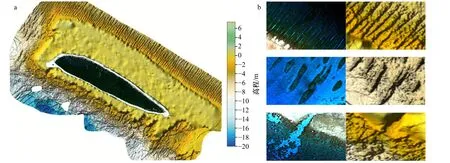
图9 反演的陆域与水下地形图（a）和地貌细节图（b）Fig. 9 Bathymetry retrieval of onshore and inversion bathymetric topographic map (a) and geomorphic details (b)

5 结论与讨论

随着多光谱卫星反演水深技术的发展，如何在小样本现场实测数据的前提下，有效提高预测精度一直是研究热点。为此，本研究基于机器学习的框架，提出了结合数据源自相关特征的空间自相关随机森林水深反演模型，并在北岛海域开展多光谱水深反演实验。通过对比改进方法与对数比值、普通克里金、随机森林方法的实验结果，得到以下结论：

（1）Stumpf 模型通过建立波段反射率与水深之间的数学关系进行预测，具有模型构造简单、对实测数据量要求较低等优势，因此得到了广泛应用。然而在水深反演过程中，受到来自深度、水质以及底质等因素变化影响，反射率与水深之间的线性关系通常不成立，而Stumpf 这类线性模型受限于模型的表达能力，渐渐无法满足日益增长的高精度遥感测深需求。对此，以RF 模型为代表的机器学习方法凭借其优异的非线性映射能力，可有效提升水深反演精度。

（2）实验表明，以OK 模型为代表的空间插值方法仅仅利用实测水深的自相关性特征信息，即取得与Stumpf 模型相似的水深预测精度。这一结果客观上印证了本文通过引入空间自相关特征信息以提高水深反演精度这一思路的可行性。对此，本文在机器学习框架下引入空间自相关特征进行建模，提出了空间自相关随机森林模型，通过深入挖掘不同数据源之间、相邻像元内部观测值的有效信息，将输入变量的统计互相关性与空间自相关性两类特征进行融合，得到了更准确的预测模型。该方法比单独使用两类特征的反演模型更具优势。SARF 模型在输入反演因子时引入两类相关性变量的信息，提高了预测过程中的信噪比，具有比传统机器学习更出色的抗噪能力。同时，SARF 模型在建模过程中充分利用训练样本的观测值，通过建立训练样本与测试样本之间的联系，从而提高有效信息的利用率。除此之外，将数据源的空间自相关特征融入机器学习算法中，有效减弱了空间非平稳性因素、极浅区域高辐射亮度值以及深水区统计值波动的影响，可显著提升不同实测数据量条件下的多光谱水深反演结果的精度。

（3）鉴于SARF 模型在遥感测深研究中取得了显著的精度优势，基于相同思路，将自相关性特征引入其他机器学习模型中亦可望取得类似的提升效果。需要注意的是，本研究区域内，水深主要集中于0～6 m浅水区，而考虑到不同研究区数据源的差异，将其应用于更多地区还需要进一步探讨。基于现有方法，未来的研究方向可考虑挖掘额外的环境信息，利用机器学习融合多变量的优势，增加更多环境相关特征（如水体指数、叶绿素浓度）并融合不同时序的多光谱影像数据源进行研究。