聚焦波作用下透水潜堤消波特性数值模拟研究

徐瑶瑶，屈科,2,3*，黄竞萱，蓝港芸，刘铁威，温博浩

( 1. 长沙理工大学 水利与环境工程学院，湖南 长沙 410114；2. 洞庭湖水环境治理与生态修复湖南省重点实验室，湖南 长沙 410114；3. 水沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410114)

1 引言

畸形波具有波高大、发生突然、能量集中和破坏力极强等特点，是众多海洋灾难事件发生的重要原因[1]。据记载，在2006–2010 年间，全球范围内约发生了78 次畸形波浪事件，其中30 次发生在海岸区域，造成了至少21 艘船只损坏（失踪）、90 人受伤、79 人死亡[2–3]。由此可见，畸形波对海岸区域的生产和人员安全构成潜在威胁。因此研究畸形波在海岸区域的传播及其与海岸建筑物的相互作用具有重要的意义。

研究表明，海洋中随机波浪群在特定位置和时间聚焦形成的聚焦波是畸形波产生的重要机理之一[4–5]。因其具有突发性和更多的波浪组分，符合自然界畸形波的特性，常被用来研究畸形波的生成、传播、破碎以及与海岸建筑物的相互作用。早期关于聚焦波的研究多基于线性波理论，如Kriebel 和Alsia[6]提出的双波列叠加模型、裴玉国[7]提出的三波列叠加模型、Johannessen 和Swan[8]使用的双傅里叶函数方法等。但是，基于线性波理论的聚焦波研究忽略了波浪非线性的影响，与实际聚焦波浪存在较大差异。在此基础上，李润峰等[9]采用非线性理论和双波列叠加的方法生成了较为合理的畸形波，该方法减小了线性波理论带来的误差。在实验室中，通常采用相速度法生成聚焦波，如Baldock 等[10]基于相速度法在二维波浪水槽开展了多个聚焦波试验。Ning 等[11]开展物理模型试验分析了非线性单向聚焦波群的演变及水质点的运动特性，并对比了一阶、二阶及非线性理论在聚焦波数值模拟中的差异。Whittaker 等[12]通过开展波浪水槽试验研究了聚焦波在斜坡上的传播、演变及破碎过程，讨论了波幅、聚焦位置、相位角对聚焦波爬坡特性的影响。除此之外，国内外的众多学者基于势流模型、非静压模型、Boussinesq 方程模型、两相流模型、高阶边界元模型等数值模型，对聚焦波浪生成、传播以及与结构物相互作用进行了系统研究。如刘必劲等[13]基于Boussinesq 方程模型对不同周期范围下的聚焦波进行了模拟，得到聚焦波波峰面值和波峰面水平速度随着周期范围缩小而增大的结论。卓晓玲[14]则采用高阶边界元模型，研究了聚焦波与直立墙的相互作用并分析了波浪频谱对波浪爬高的影响。

为保护海岸结构物免受极端波浪的破坏，沿海地区修建了众多的防护工程。潜堤因具有较好的适用性和防护功能，广泛应用于我国沿海地区。前人关于波浪与潜堤相互作用的研究大多基于不透水潜堤[15–22]，如边峰等[16]采用物理模型试验的方法讨论了矩形、梯形、三角形、半圆形4 种不同结构形式潜堤的消浪特性，发现堤顶宽度的增大有利于增强潜堤的消浪效果。郑艳娜等[17]通过物理模型试验研究了规则波作用下梯形和矩形组合式潜堤的消浪特性，结果表明波高越大，堤顶水深越小，组合式潜堤排数越多，消浪效果越好。Han 和Dong[19]利用光滑粒子法研究了孤立波在潜堤上的传播和演变规律，发现堤顶水深对潜堤消浪特性具有显著的影响。Liang 等[20]分析了潜堤间距对规则波和非规则波潜堤消波特性的影响，当淹没深度等于波高时，最佳的潜堤间距比为1.11。Li 等[21]基于CIP 模型研究了聚焦波与不透水潜堤的相互作用，分析了聚焦波在潜堤上的波浪传播变形和演化特征。近些年，透水潜堤作为一种综合性能更优的结构被广泛应用于海岸防护工程建设。国内外学者针对透水潜堤的消浪特性从理论分析[23–24]、物理试验[25–27]、数值模拟[28–35]3 个方面开展了大量研究。如Sollitt 和Cross[23]采用推导的多孔介质理论求解防波堤内的阻尼波分量，预测反射和透射波分量。基于Sollitt 和Cross[23]的多孔介质理论，Twu 和Liu[24]建立了理论数值模型，研究潜堤的孔隙率、数量、高度、宽度等因素对波浪阻尼特性的影响。蒋昌波等[25]和刘胜宇等[26]针对孤立波、规则波、椭圆余弦波与透水潜堤的相互作用开展了大量的物理模型试验，结果表明透水潜堤对非线性波浪的耗散作用优于线性波浪。除了理论与物理模型的研究，国内外学者基于多孔介质理论，针对透水潜堤的消波特性，开展了相关的数值模拟研究。如Hieu 和Tanimoto[30]采用VOF 方法，基于两相流模型研究了规则波与透水潜堤之间复杂的相互作用，得出惯性力和拖曳力系数固定时，透水潜堤最优消波孔隙率为0.6。Ma 等[31]基于非静压模型NHWAVE研究了孤立波与矩形透水潜堤的相互作用，结果表明非静压模型相比两相流模型能较大程度地提高计算效率。Behera 和Khan[33]在小振幅水波理论的假设下，采用边界元方法研究了不同结构参数对双梯形多孔结构消波特性的影响。Booshi 和Ketabdari[34]利用PLICVOF 研究了多孔防波堤对孤立波的消波特性，并且讨论了孔隙率、阻力、惯性系数等参数的影响。Zhang等[35]基于两相流模型研究了波浪–透水潜堤–透水海床相互作用的机制，得出增加防波堤的孔隙率和潜堤高度会增大波能耗散的结论。

虽然前人针对透水潜堤的消波特性开展了一定的理论、试验和数值模拟研究，但是关于透水潜堤对聚焦波消波特性的研究成果相对较少。本文基于非静压数值计算模型，系统研究了聚焦波作用下透水潜堤的消波特性。通过设置合理的计算工况，详细分析了波高、堤顶水深、谱峰周期、孔隙率，以及堤顶宽度5 种因素对透水潜堤消波特性的影响。与此同时，本文将透水潜堤的计算结果同不透水潜堤的计算结果进行了对比分析。研究结果可为海岸工程防护建设提供相关参考。

2 数值模型

2.1 控制方程

非静压数值波浪模型NHWAVE 的控制方程为不可压缩流Navier-Stokes 方程在 σ坐标系下的表达式[36]:

2.2 湍流模型

2.3 波浪的边界条件

本文通过在计算入口边界施加速度和波面高程的方法生成聚焦波，对于入射波高较大的聚焦波，不同波组分的波–波相互作用不可忽略，因此，本文采用了二阶聚焦波理论，表达式为

波浪与海岸结构物相互作用的过程中会发生能量的消耗和转换，本文使用以下公式来计算聚焦波通过透水潜堤时的动能（KE）、势能（PE）和总能（TE）。

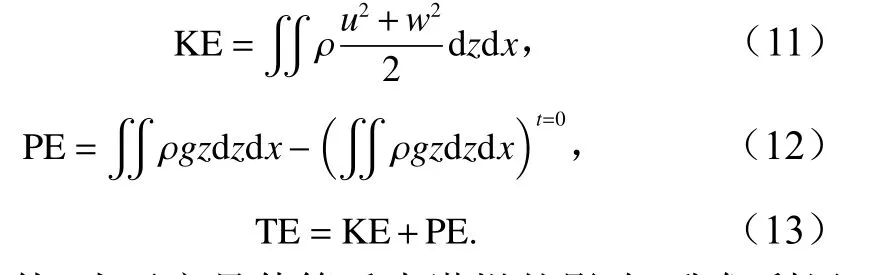
此外，为了定量估算透水潜堤的影响，我们利用特定位置的最大波幅公式计算了波浪衰减系数为

3 模型验证

3.1 聚焦波在不透水潜堤上的传播验证

本节基于非静压数值模型NHWAVE 建立二维数值波浪水槽，参考Li 等[21]在浙江大学海洋学院实验室的地形和工况，数值模拟了聚焦波与潜堤相互作用的过程，并将数值计算结果与物理试验得到的自由液面数据进行对比，以验证非静压模型模拟聚焦波在潜堤上传播的能力。实验水槽长为75 m，宽为1.8 m，高为2 m，在距造波机32 m 的位置设置一个长为3.08 m、高为0.36 m、坡度为1∶2.19 的梯形潜堤，实验堤前水深为0.5 m，共设置有G1、G2、G3、G4、G5、G6 共6 个波高仪，波高仪 G3 设置在波浪聚焦位置处，波浪组分与物理试验一致为N=29。

采用与实验相同的设置来建立数值水槽，计算区域如图1 所示。其中，计算区域长为60 m，高为2 m，入口为造波边界，距出口边界8 m 处设置数值消波区域，以防止波浪反射。潜堤距入口18 m，聚焦位置在波高仪G3 处，聚焦时间tf=20 s。x方向为聚焦波的传播方向，网格大小 Δx= 0.03 m；z方向为水深方向，共划分20 层网格。验证工况如下表1 所示。

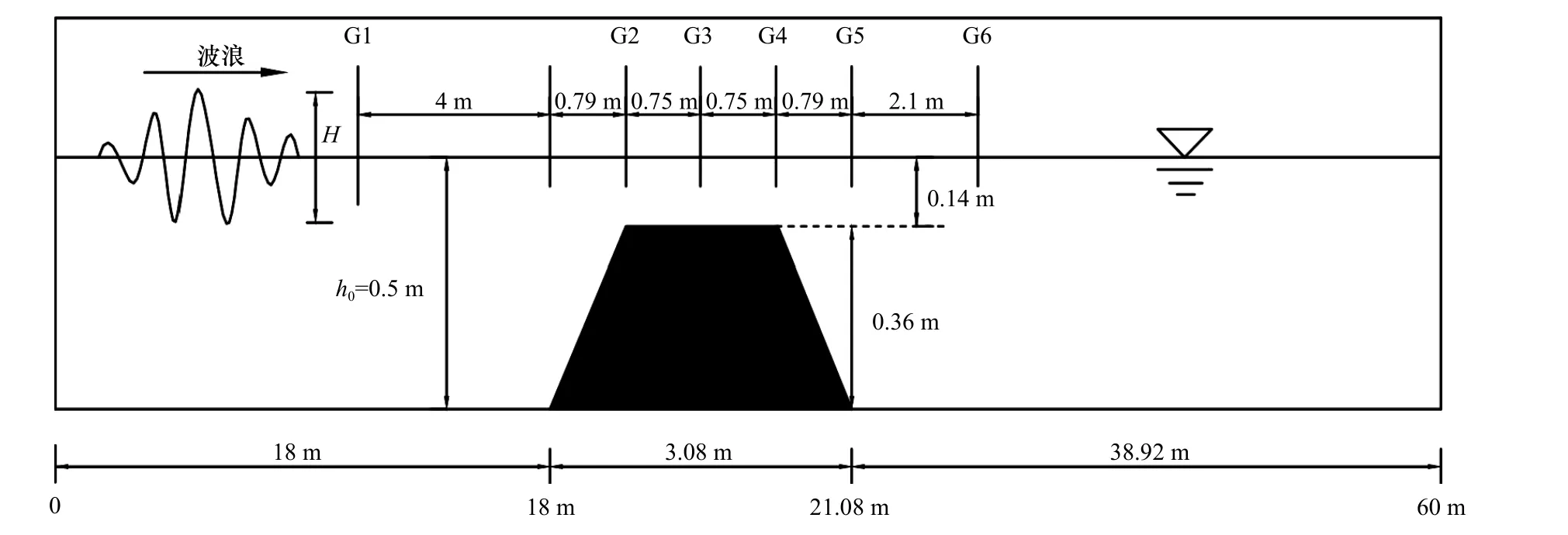
图1 聚焦波与不透水潜堤作用数值计算布置Fig. 1 Computational layout of focused wave impacting impermeable breakwater

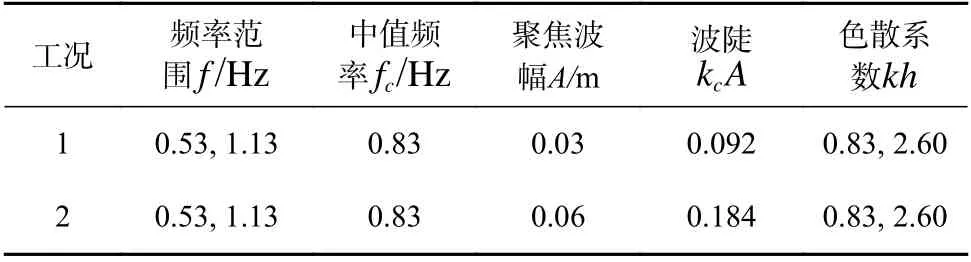
表1 验证工况参数Table 1 Parameter setup of verification conditions

图2 为不同工况的两种聚焦波在6 个测点处的自由液面时程曲线图。通过对比可以看出数值计算与实验结果基本吻合。同时与文献[21]中基于CIP模型的模拟结果对比，可以看出本文在对波峰的捕捉上要更准确。但在堤后几个测点上仍与试验值存在一定差异，这是由于聚焦波具有强非线性作用，与潜堤作用后的破碎现象较复杂。总体而言，本文采用的模型具备模拟聚焦波在潜堤上传播、变形的能力。

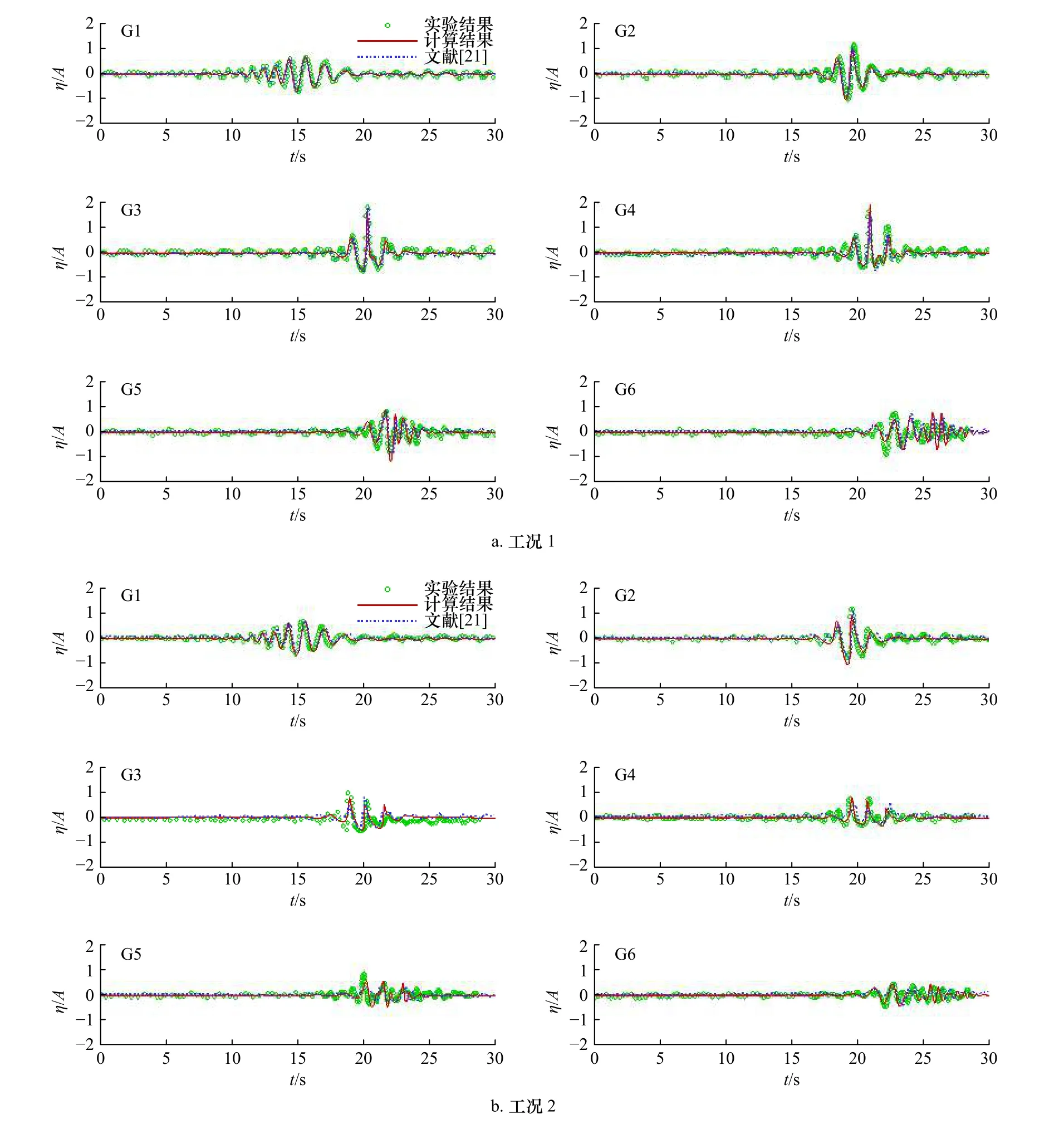
图2 聚焦波作用下不同水位测点自由液面时程曲线图Fig. 2 Time series of water elevation recorded at different wave gauges under focused wave

3.2 规则波在透水潜堤上的传播验证

为了验证波浪在透水潜堤上的传播过程，基于Hieu 和Tanimoto[30]的波浪水槽试验，本节开展了相应的数值模拟研究。试验采用的水槽大小为18 m×0.4 m×0.7 m，试验堤前水深为0.376 m，透水潜堤放置在距造波板10.5 m 的位置，高为0.33 m，基底宽为1.16 m，多孔介质的中值粒径d50=0.025 m，孔隙率n=0.45。

数值模拟参数与实验保持一致，计算布置如图3所示，计算区域总长为28 m，透水潜堤坡脚距左侧造波边界为9.57 m，在出口边界处设置6 m 长的消波区，以防止波浪反射。透水潜堤前后共设置6 个水位测点，分别位于x=8.1 m，x=9.4 m，x=9.9 m，x=10.75 m，x=11.44 m，x=12.04 m。x方向为波浪传播方向，网格大小 Δx= 0.01 m；z方向为水深方向，共划分20 层网格。验证工况的水深、波高和周期分别为0.376 m、0.092 m 和1.6 s，多孔介质参数取值为 α =200， β=1.1[31]。为了更加直观地判断NHWAVE 数值模型的计算精度，本文引用Warner 等[42]建议的skill 数来展开分析。关于skill 数的定义采用Willmott[43]的方法，具体为

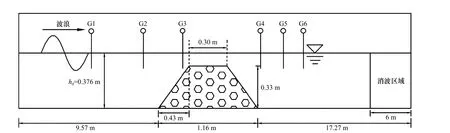
图3 规则波与透水潜堤作用数值计算布置Fig. 3 Computational layout of regular wave impacting permeable breakwater

图4 展示了规则波作用下不同水位测点的自由液面时间序列数值模拟结果与试验结果的对比情况。结果表明，6 个测点位置的skill 数均在0.85 以上，说明计算结果与试验结果对比吻合较好，表明该模型有计算波浪在多孔介质内流动的能力。

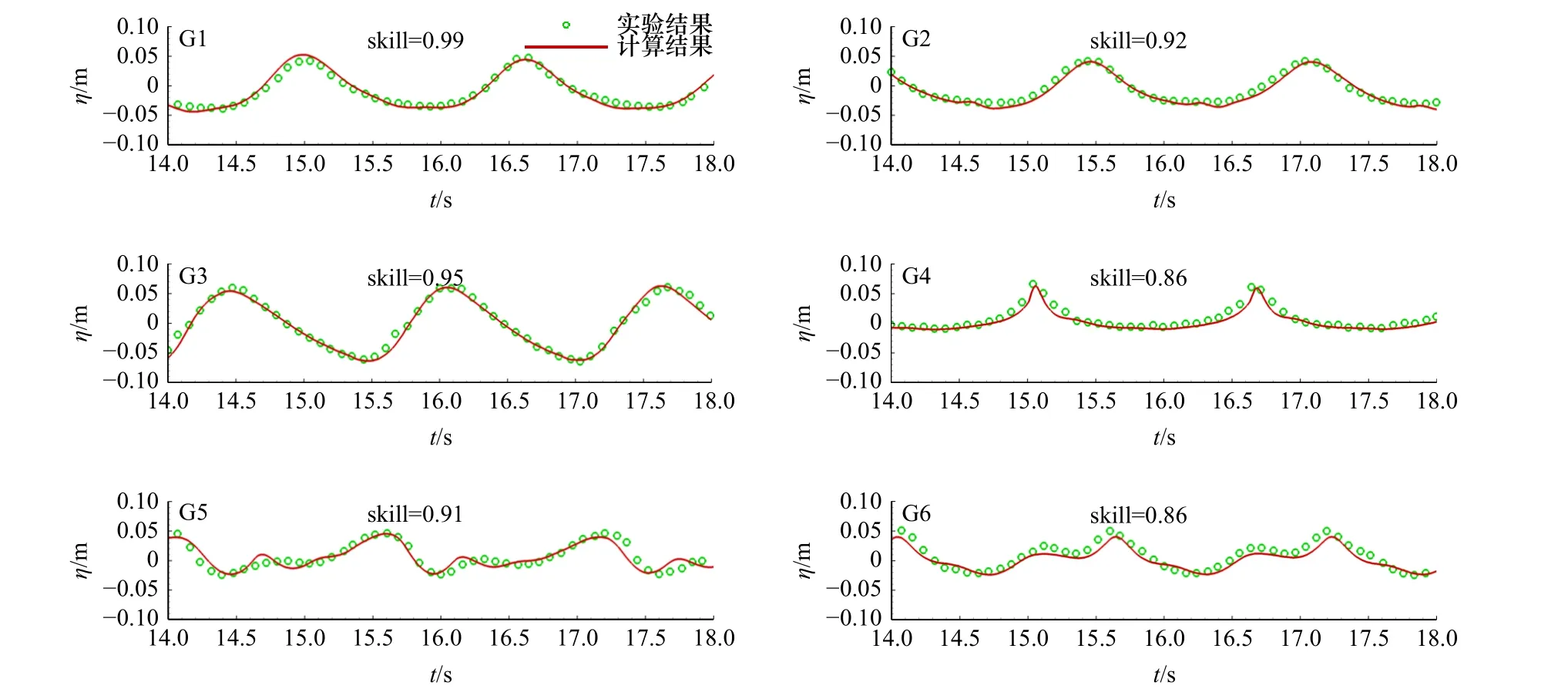
图4 规则波作用下不同水位测点自由液面时程曲线图Fig. 4 Time series of water elevation recorded at different wave gauges under regular wave

4 结果讨论与分析

本文系统研究了聚焦波与透水潜堤相互作用的水动力过程，讨论了不同入射波高Hs、堤顶水深h、谱峰周期Tp、孔隙率n，以及潜堤宽高比ε 5 个因素对透水潜堤消波特性影响，并与不透水潜堤对比。计算区域布置如图5 所示，计算区域长为20 m，潜堤剖面为等腰梯形，长为0.9 m，高为0.25 m，潜堤两侧坡度为5 ∶7，放置在x=7.3 m 的位置，计算区域右侧设置6 m消波区域，在潜堤附近共设置36 个水位计，间距为0.1 m，主要分析x=7.6 m，x=7.8 m，x=8.2 m，x=9.0 m 4 个测点处的波高变化情况。x方向为聚焦波传播方向，设置网格分辨率 Δx= 0.01 m，竖直方向共划分20 层网格。

图5 聚焦波与透水潜堤作用数值计算布置Fig. 5 Computation layout of focused wave impacting permeable breakwater

设置数值模拟标准工况为：波高Hs=0.075 m，水深h=0.375 m，谱峰周期Tp=1.2 s，中值粒径d50=0.025 m，孔隙率n=0.45。基于标准工况，研究5 种波高（Hs=0.037 5 m、0.056 3 m、0.075 m、0.094 m、0.113 0 m）、8 种堤顶水深（h=0.005 m、0.035 m、0.065 m、0.105 m、0.115 m、0.125 m、0.135 m、0.145 m）、8 种谱峰周期（Tp=1.2 s、1.3 s、1.4 s、1.5 s、1.6 s、2.0 s、2.5 s、3.0 s）、5 种孔隙率（n=0.35、0.40、0.45、0.50、0.55）、5 种堤顶宽度（B=0 m、0.034 m、0.2 m、0.4 m、0.612 5 m）一系列组合工况对聚焦波作用下潜堤消波特性的影响。在接下来的数值计算中，波浪组分数设为N=30。

4.1 水动力特性

本节对聚焦波在潜堤上传播的水动力过程展开讨论，通过研究聚焦波的最大波幅衰减系数和总能量耗散系数的变化，分析聚焦波作用下透水和不透水潜堤的消波特性。采用的聚焦波工况为：波高Hs=0.075 m，水深h0=0.375 m，谱峰周期Tp=1.2 s。透水潜堤由均匀多孔介质组成，具体参数为：中值粒径d50=0.025 m，孔隙率n=0.45。潜堤高为0.25 m，底部宽为0.9 m，两侧陡坡坡度比为5∶7。聚焦波以波峰聚焦的形式在x=7.3 m 处聚焦。图6 给出了聚焦波在透水潜堤和不透水潜堤上传播的自由液面时程变化图。如图6a 所示，在G1、G9 两个测点的位置，聚焦波尚未传播至潜堤，此时透水和不透水潜堤工况下的波面时间序列几乎没有区别。而聚焦波传播至潜堤时，如图6b 和图6c所示，透水潜堤工况下聚焦波波幅的衰减明显高于不透水潜堤。同时随着潜堤斜坡上水深减小，波高与水深的比值增大，聚焦波的波峰变得陡尖，波形呈不对称分布，表现出较强的非线性。如在G18 测点的位置处，聚焦波变形导致高波幅出现且主波周围的波列也表现出不对称性。随后，由于水深的急剧减小，无法继续维持大波浪的传播，波浪在堤后（G26 测点）发生破碎，波高急剧下降，达到潜堤消能的目的。图7 为不同时刻的流场速度云图，随着聚焦波的传播，流场速度逐渐增大，当聚焦波传播至潜堤时，如图7a 和图7c所示，波浪开始变形；当波浪传至潜堤堤顶中间的位置时，如图7b 和图7d 所示，聚焦波的前波开始趋于垂直，接近破碎状态。图8 为聚焦波与潜堤作用的最大波幅变化，由图可知，聚焦波在不透水潜堤上传播的最大波幅总是大于在透水潜堤上传播的最大波幅，最大波幅衰减率分别为0.26 和0.38。此外，透水潜堤最大波幅的位置出现在潜堤内侧坡顶处，而不透水潜堤出现在内侧坡脚处，这反映出透水潜堤在消波性能方面的优越性。这是因为与透水潜堤相互作用时，聚焦波会通过透水潜堤的孔隙结构发生渗流。由于聚焦波浪具有强非线性，波高更大、能量更集中，与潜堤内的水-孔隙结构发生相互作用，造成了波能的大幅耗散。图9 为整个流场水体动能、势能和总能量变化的时间序列，可以看出，随着聚焦波波群完全进入计算域，能量逐渐增加并达到最大值。随后由于潜堤的耗散作用，水体的动能和势能减小，透水潜堤时波能的耗散作用可达到38.4%，而不透水潜堤仅为7%。

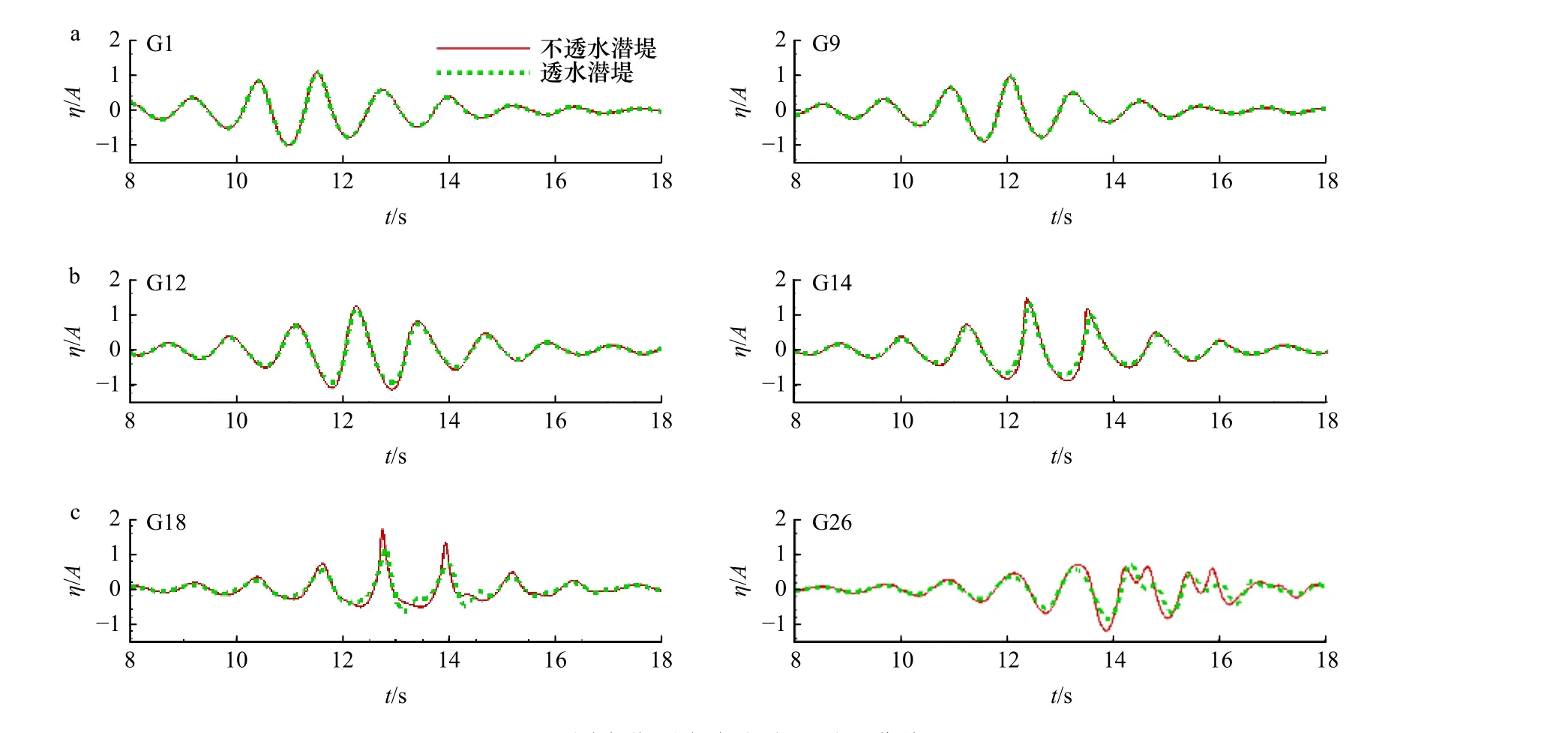
图6 不同水位测点自由液面时程曲线Fig. 6 Time series of water elevation recorded at different wave gauges

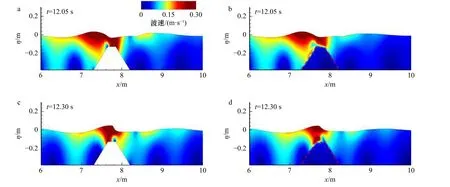
图7 不同时刻流场速度分布云图Fig. 7 Snapshots of water body velocity distribution at different time instances

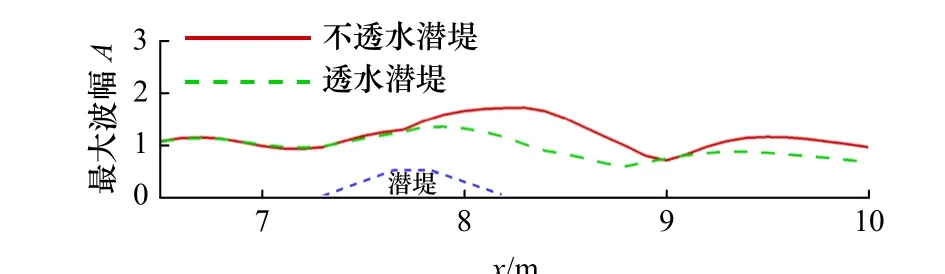
图8 聚焦波与潜堤作用最大波幅变化Fig. 8 Variations of the largest wave amplitude of focused wave along the breakwater

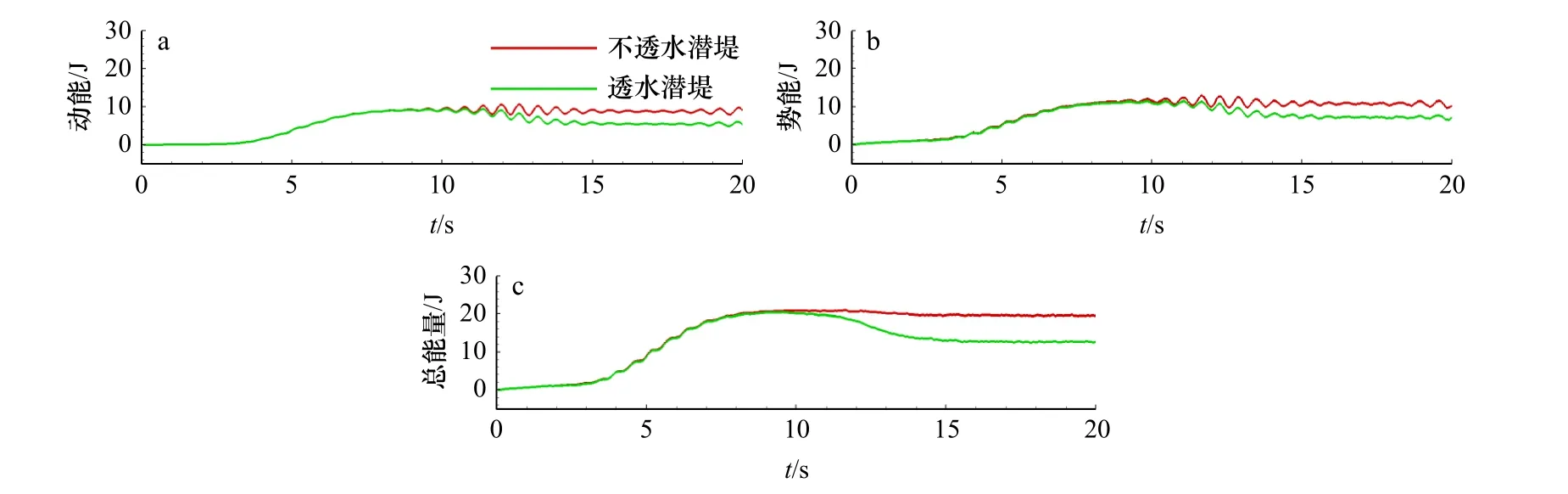
图9 水体动能（a）、势能（b）、总能量（c）时程曲线Fig. 9 Time series of kinetic energies (a), potential energies (b), total wave energies (c) of the whole water body

4.2 波高的影响

本节研究波高对透水潜堤消波特性的影响，堤顶水深h= 0.125 m，谱峰周期Tp=1.2 s，透水潜堤介质中值粒径d50=0.025 m，孔隙率n=0.45，共选取 5 种不同的入射波高，分别为Hs=0.037 5 m、0.056 3 m、0.075 m、0.094 m、0.113 0 m，并与不透水潜堤进行对比分析。根据不同的波浪工况，利用空水槽造波确定波浪聚焦位置，随波高增加，聚焦位置稍微后移。为了控制单一变量，选取的数值计算工况总保证潜堤的外侧坡脚固定在聚焦位置处。图10 分别为不同波高条件下，透水潜堤和不透水潜堤的最大波幅衰减系数和波浪总能量耗散系数的变化图。可以看出，聚焦波的最大波幅衰减系数和总能量耗散系数均随波高的增加而增大。这是因为随着波高的增加，作用在潜堤上的波浪蕴含的能量越大，相互作用越剧烈。同时，随着波高的增加，聚焦波非线性作用增大，自由表面的变形也更加剧烈，波浪更易发生破碎。在波高为0.037 5 ～0.113 0 m 的范围内，不透水潜堤的最大波幅衰减系数为0.13～0.28，总能量耗散系数为0.08～0.24，而透水潜堤的最大波幅衰减系数为0.34～0.43，总能量耗散系数为0.38～0.43。综上，透水潜堤消波效果更好。

图10 不同波高条件下最大波幅衰减系数（DA）（a）和总能量耗散系数（DE）（b）变化Fig. 10 Variations of maximum amplitude attenuation coefficient (DA) (a) and total energy dissipation coefficient (DE) (b) under different wave height

4.3 堤顶水深和谱峰周期的影响

本节讨论堤顶水深和谱峰周期对透水潜堤消波特性的影响，并与不透水潜堤的情况展开对比。当考虑堤顶水深的影响时，共选取了8 种堤顶水深，分别为h=0.005 m、0.035 m、0.065 m、0.105 m、0.115 m、0.125 m、0.135 m、0.145 m。图11a 展示了在入射波高Hs=0.075 m，谱峰周期Tp=1.2 s，透水潜堤的中值粒径d50=0.025 m，透水潜堤孔隙率n=0.45 时，不同堤顶水深条件下聚焦波最大波幅衰减系数的变化趋势。可以看到，随着堤顶水深的增加，透水潜堤的最大波幅衰减系数呈单调减小趋势。当堤顶水深大于0.065 m时，最大波幅衰减系数的变化趋势减缓。但是对于不透水潜堤而言，最大波幅衰减系数随着堤顶水深的变化趋势并不显著。不同堤顶水深条件下的平均最大波幅衰减系数为0.287。 图11b 展示了不同堤顶水深条件下，总能量耗散系数的变化趋势。对于透水潜堤而言，不同堤顶水深条件下，波浪总能量耗散系数呈单调减小趋势。堤顶水深越小，波浪破碎强度越大，透水层消耗的波浪能量就越多。对于不透水潜堤而言，在堤顶水深小于0.065 m 时，波浪总能量耗散系数随水深的变化趋势不显著，平均能量耗散系数为0.386。这表明当堤顶水深小于一定程度时，不同堤顶水深条件下，波浪破碎强度及底部摩阻引起的波浪耗散变化趋势不明显。

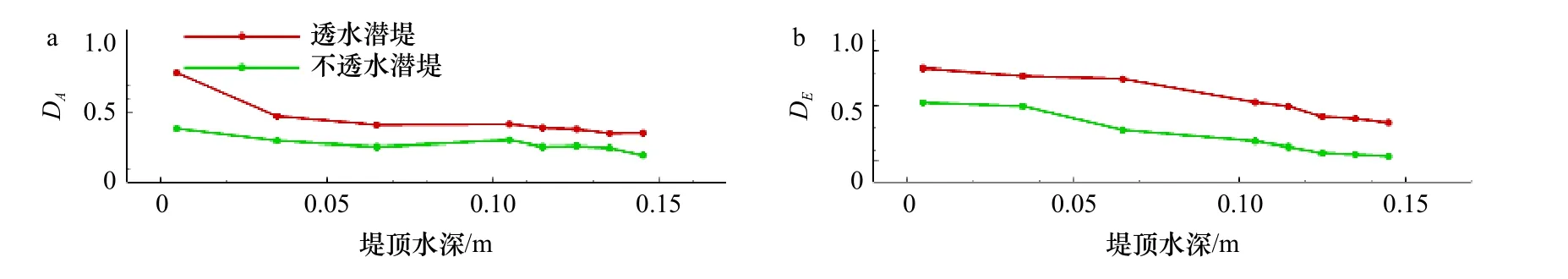
图11 不同堤顶水深条件下最大波幅衰减系数（DA）（a）和总能量耗散系数（DE）（b）变化Fig. 11 Variations of maximum amplitude attenuation coefficient (DA) (a) and total energy dissipation coefficient (DE) (b) under different water depth above the submerged breakwater

本节还研究了不同谱峰周期对潜堤消波特性的影响，选取8 种不同的谱峰周期情况，分别为Tp=1.2 s、1.3 s、1.4 s、1.5 s、1.6 s、2.0 s、2.5 s、3.0 s。图12 给出了不同谱峰周期下聚焦波最大波幅衰减系数和总能耗散系数的变化趋势。从图12a 中可以看出，虽然随着谱峰周期的增加，最大波幅衰减系数呈非线性变化趋势，但整体而言最大波幅衰减系数呈现减小的变化趋势。由图12b 可知，随谱峰周期的增加，波能耗散系数整体呈减小趋势。同时可以看出，透水潜堤的消波特性受谱峰周期的影响相较不透水潜堤更为显著。与前人的研究成果一致，潜堤对长周期波的耗散作用要小于对短周期波的耗散作用。

图12 不同谱峰周期条件下最大波幅衰减系数（DA）（a） 和总能量耗散系数（DE）（b）变化Fig. 12 Variations of maximum amplitude attenuation coefficient (DA) (a) and total energy dissipation coefficient (DE) (b) under different spectral peak period

4.4 孔隙率的影响

孔隙率是影响透水潜堤消波能力的重要因素之一，因此本节系统研究了透水潜堤的孔隙率对聚焦波通过潜堤时波幅衰减系数和能量耗散系数的影响。在入射波高Hs=0.075 m，堤顶水深h=0.125 m，谱峰周期Tp=1.2 s，透水潜堤的中值粒径d50=0.025 m 时，选取5 种不同的透水潜堤孔隙率，分别为n=0.35、0.40、0.45、0.50、0.55，对不同孔隙率条件下透水潜堤的消波作用展开研究，并与不透水潜堤进行对比分析。波浪通过透水结构是聚焦波波–波相互作用的非线性过程，在这个过程中波浪与潜堤的作用更加剧烈，波能耗散也更充分。图13a 给出了5 种不同孔隙率条件下聚焦波最大波幅衰减系数的变化，由图可知，孔隙率的增加显著增大了波幅的衰减，最大波幅衰减系数从0.26 增加到0.41。图13b 为聚焦波总能量耗散系数的变化，可以看出，随着孔隙率从0 增加到0.55，能量耗散系数从0.07 增加到0.55，基本呈线性增长。

图13 不同孔隙率条件下最大波幅衰减系数（DA）（a）和总能量耗散系数（DE）（b）变化Fig. 13 Variations of maximum amplitude attenuation coefficient (DA) (a) and total energy dissipation coefficient (DE) (b) under different porosity

4.5 堤顶宽度的影响

为研究聚焦波作用下不同堤顶宽度对潜堤消波特性的影响，设置入射波高Hs=0.075 m，堤顶水深h=0.125 m，谱峰周期Tp=1.2 s，透水潜堤的中值粒径d50=0.025 m，透水潜堤孔隙率n=0.45，共选取5 种堤顶宽度，分别为B=0 m、0.034 m、0.2 m、0.4 m、0.612 5 m。潜堤保持堤高为0.25 m，底宽为0.9 m 不变，前坡脚固定在x=7.3 m 处，分别讨论最大波幅衰减系数和波浪总能量耗散系数的变化。由图14a 可知，随着堤顶宽度增大，透水和不透水潜堤的最大波幅衰减系数分别从0.32 增加到0.44 及0.17 增加到0.37。图14b 为聚焦波总能量耗散系数的变化趋势，随堤顶宽度的增加，总能量耗散系数呈线性增长的趋势。随潜堤堤顶宽度从0 增加到0.612 5 m，不透水潜堤和透水潜堤的能量耗散系数分别从0.04 增加到0.18 及0.32 增加到0.54。结果表明堤顶宽度是影响潜堤消波特性的关键因素。随着堤顶宽度增大，潜堤形状由三角形变为梯形，聚焦波在潜堤堤顶传播时间延长，与透水结构作用越充分，波能损耗越严重，这与边锋等[16]的研究结果是一致的。

图14 不同堤顶宽度条件下最大波幅衰减系数（DA）（a）和总能量耗散系数（DE）（b）变化Fig. 14 Variations of maximum amplitude attenuation coefficient (DA) (a) and total energy dissipation coefficient (DE) (b) under different crest width of submerged breakwater

5 结论

本文采用非静压数值波浪模型NHWAVE，建立高精度数值波浪水槽，基于二阶聚焦波理论，系统研究了聚焦波作用下透水潜堤消波特性，分析了不同波高、堤顶水深、谱峰周期、孔隙率，以及堤顶宽度对透水潜堤消波性能的影响，并且与不透水潜堤进行了对比。主要结论如下：

（1）由于多孔介质的存在，聚焦波可以通过透水潜堤，大部分波分量与潜堤透水结构发生剧烈的紊动，导致波幅降低了38%，总波能损失高达40%，同种工况下，消波效果优于不透水潜堤。

（2）其他条件不变的情况下，随入射波高的增加，聚焦波的非线性作用增大，潜堤的消波效果也更明显。

（3）透水潜堤的消波性能受堤顶水深变化的影响明显，堤顶水深越高，波浪经过潜堤时越不容易发生破碎，消波效果越差，但在堤顶水深小于一定程度时，波能耗散变化趋势不明显。

（4）潜堤对长周期波的耗散作用小于对短周期波的耗散作用。

（5）透水潜堤的孔隙率对其消波性能起着重要的作用，n从0 增加到0.55 会导致最大波幅降低15%，能量衰减48%。

（6）堤顶宽度越大，潜堤消波效果越好，基本呈线性关系。对于透水潜堤，当堤顶宽度为0.612 5 m 时，能量损失接近54%，比不透水潜堤对入射波能的消减增加36.1%。