摭谈“尺规作图”问题的育人价值*

钟珍玖 张炜钰 (江苏省江阴市第一初级中学 214432)

1 尺规作图问题概述

所谓“尺规作图”就是限定作图工具为没有刻度的直尺和圆规来画几何图形．最为著名的是三大几何作图问题：化圆为方、三等分任意角、倍立方.这三大“尺规作图”问题在数学史上引起了很多数学家和数学爱好者的兴趣，直到1673年，笛卡尔创建解析几何以后，通过“证伪”说明了三大作图问题的不可能性，问题才得以解决．但是，人们对尺规作图问题研究的步伐还在延续．

2 尺规作图问题的特征

尺规作图问题由于其鲜明的历史背景，决定了其特有的文化意蕴，在尺规作图的发展历程中充满了故事．解决尺规作图问题的过程就是画图探究的过程，通过分析推理，探索把问题转化为何种基本尺规作图问题．作图问题的方法不唯一，因此作图方法具有开放性．

2.1 尺规作图问题的文化性

尺规作图起源于古希腊人对于几何作图问题的研究，公元前5世纪时数学史上的三大作图问题被提出．此后的二千多年中很多的数学家和数学爱好者都对三大作图问题产生了浓厚的兴趣，直到1873年万芝尔在研究阿贝尔定理的化简时才证明了三等分任意角和倍立方体的尺规作图不可能问题．这些经典的数学故事,可以极大地提高学生学习数学的兴趣，增强学生对数学发展史的了解，更好地传播数学文化．尺规作图问题不仅提供了存在性的证明方法，还产生了“证伪”的思维方式，推动数学的发展，具有丰富的文化价值．

2.2 尺规作图问题的探究性

尺规作图问题虽然作图条件给定，作图结果也确定，但是尺规作图问题并不等同于一般的几何演绎推理问题，尺规作图问题所要作的图形结果是未知的，需要学生借助分析法逆向思考，不断探究才能作出符合条件的图形，有时作图的方法也具有多样性，并且有的作法不容易发现，尺规作图的问题充满着探究的味道．

2.3 尺规作图问题的创新性

很多尺规作图问题，其构图方法具有多样性，往往需要借助直观猜想，结合逻辑推理进行广泛的联想，不仅要求作图者思维缜密，更要能突破思维的局限，敢于和善于创新才能解决问题．从形式上看尺规作图问题是作图方式上的创造，实质上是思维方式的创新，创新性是尺规作图问题的最为重要的特征．

3 尺规作图问题的育人价值及教学建议

尺规作图问题的结果是作出符合条件的图形，但仅有画图技能是不能解决问题的，需要学生具有较强的逻辑推理能力和探究意识，还需要思维灵活、缜密、创新．从尺规作图问题的特征来看，尺规作图问题有如下的育人价值.

3.1 培养学生探究与推理融汇的意识

从教学实践来看，很多一线教师仅仅把尺规作图看成是画图技能的训练，不重视画图原理的教学，从而失去培养学生逻辑推理能力的宝贵机会．实际上，数学教材中的尺规作图问题也是培养学生探究意识和探究能力的很好素材，教师要设计好呈现方式和呈现的顺序，让学生学会在推理中探究画图方法，在多样性的画图方法探究中增强推理意识和推理能力．

案例1苏科版八年级上册“用直尺和圆规画线段AB的垂直平分线”．

在学习了垂直平分线的性质和判定定理的基础上，苏科版教材编排了用直尺和圆规画线段AB的垂直平分线，这样的安排从知识的应用和思维的顺畅来看比较自然合理，但是失去了画线段的垂直平分线的“探究味”．笔者尝试在学习了等腰三角形的性质之后，再要求学生用尺规作图画线段AB的垂直平分线，这样的安排需要学生充分领会尺规作图的特点，问题具有很强的探究性、开放性、发散性.学生得到以下两种画法.

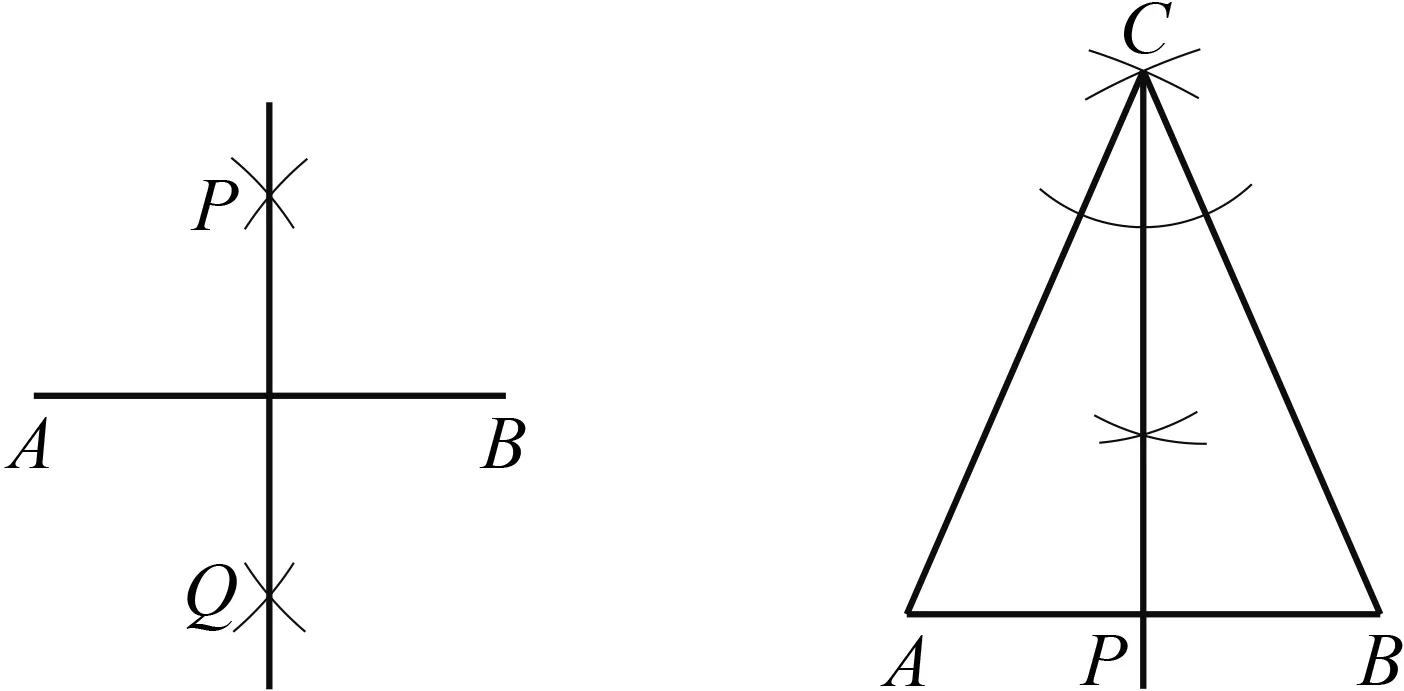
图1 图2

3.2 培养直观猜想与推理论证结合的习惯

尺规作图问题的特征决定了其必然为学生学习的难点，在解答时需要有科学的思维方式，以分析法为基础，借助逻辑推理解决问题，或者以直观猜想为思维的突破口，再进行推理论证，验证猜想的正确性．

案例2如图3，在平面直角坐标系中，已知点B的坐标为(6,4)．

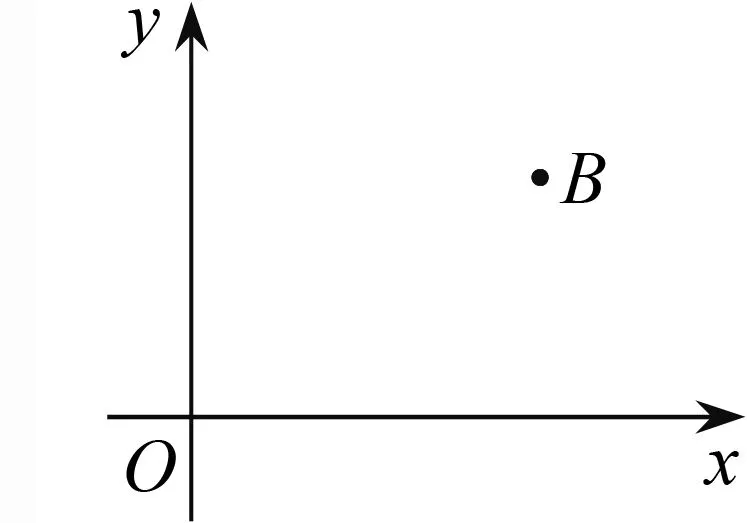
图3

(1)请用直尺(不带刻度)和圆规作一条直线AC，它与x轴和y轴的正半轴分别交于点A和点C，且使∠ABC=90°，△ABC与△AOC的面积相等．(作图不必写作法，但要保留作图痕迹)

(2)问：(1)中这样的直线AC是否唯一？若唯一，请说明理由；若不唯一，请在图中画出所有这样的直线AC，并写出与之对应的函数表达式．[1]

此问题的两个小题实质是同一个问题，命题者为了使试题有一定的梯度，降低试题的难度设置了两个问题．所作直线AC要求满足∠ABC=90°，△ABC与△AOC的面积相等两个限制条件，即使用分析法假设直线AC已经作好，因为点A和点C都是动点，很难确定点A,C的位置，由∠ABC=90°直观地猜想，当四边形OABC是矩形时，显然也满足△ABC与△AOC的面积相等，从而问题(1)就很容易解决．问题(2)的解决依然依赖几何直观，因为问题中只有点O和点B是定点，当AC是线段OB的垂直平分线时，OA=AB，OC=BC，由等边对等角易得∠ABC=∠AOC=90°，△ABC与△AOC的面积也相等．

从这两个问题的解决过程来看，由特殊情形入手，通过直观猜想发现问题的解决策略，再运用逻辑推理证明猜想的正确性，从而解决复杂的尺规作图问题，这种方法贯穿于整个几何的学习过程中.教师在教学过程中，要有意识加强示范和引导，更多地创设有利于培养学生直觉思维的情境，潜移默化地让学生形成把直观猜想与推理论证相结合的习惯，为学生的发现和创造打下坚实的基础．

3.3 培养科学思辨与创新思维的精神

尺规作图问题的结果是确定的几何图形，但是实现结果的方法往往是多样的，表现出较大的灵活性，构图方法创新性强，解决问题的过程伴随着分析、推理、判断等思维活动，能够通过作图认识问题的本质，辨别思维的对错与优劣．

案例3用尺规作图作圆的内接正三角形．

苏科版九年级下册“正多边形与圆”一节中，教材“数学实验室”问题设置：用尺规作图画圆的内接正六边形，再让学生画圆的内接正三角形和内接正十二边形．把问题直接改编为用尺规作图作圆的内接正三角形，缺少了作正六边形的思维脚手架，解决问题需要有创新构图能力和创新思维的方法．

方法1 如图4，在⊙O上任取一点A，以点A为圆心、OA为半径画弧与⊙O交于点B，再以点B为圆心、OA为半径画弧交⊙O于点C，以此方法依次作点D,E，则△ACE为⊙O的内接正三角形．

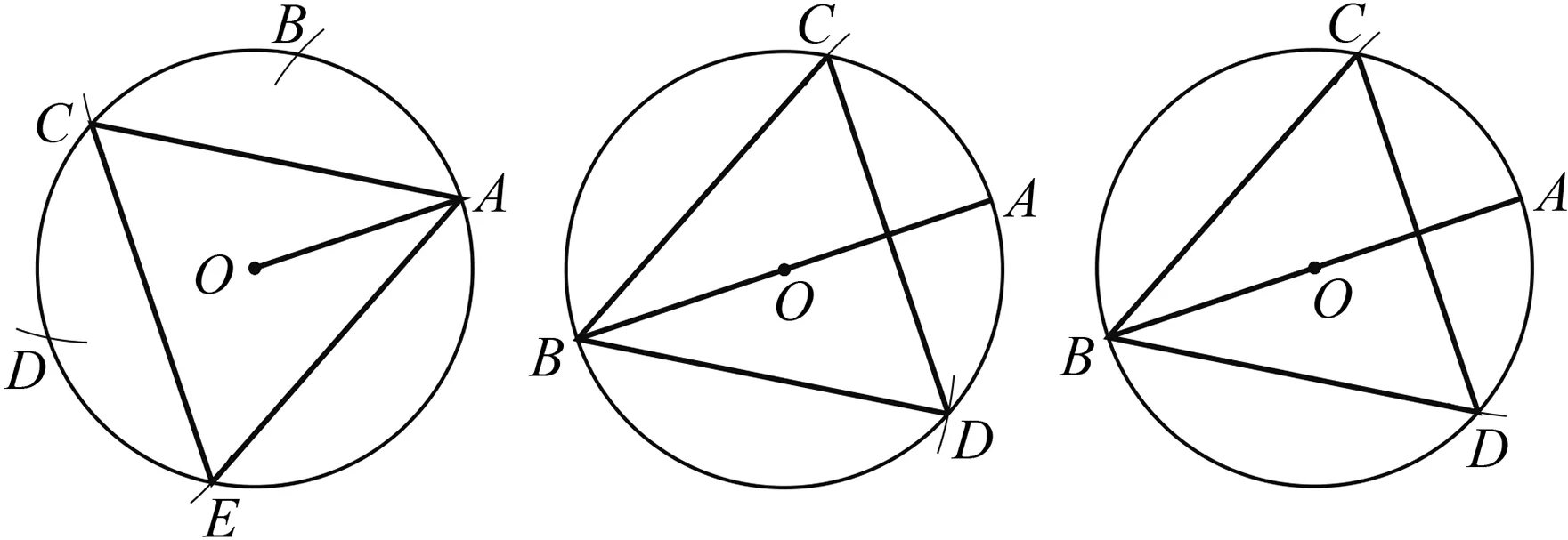
图4 图5 图6

方法2 如图5，经过圆心O作任意一条直径AB，以点A为圆心、OA为半径画弧与⊙O交于点C，以点B为圆心、CB为半径画弧交⊙O于点D，则△BCD就是所要作的⊙O的内接正三角形．

方法3 如图6，经过圆心O作任意一条直径AB，以点A为圆心、OA为半径画弧与⊙O交于点C,D，则△BCD为⊙O的内接正三角形．

方法2先画了60°的圆周角，从而可以构造120°的圆心角，然后利用在同圆或等圆中，相等的弦所对的圆心角相等，作出圆的内接等边三角形．方法1是把问题先转化为画圆的内接正六边形，然后间隔一个顶点连结就完成作图，其本质依然是构造120°的圆心角，利用圆的性质来作正多边形．方法3也是构造120°的圆心角，从整体的视角出发构图，画法简洁，思维的创新度高．通过画法的对比，可以有效提高学生的思辨能力和思维方式．在尺规作图问题教学中，建议教师对教材中的问题进行适当的改编或者改变呈现的方式，鼓励学生思维创新，在思维的比较和碰撞中提高思辨能力，提升核心素养．

尺规作图问题不仅能培养学生的逻辑推理能力，在培养学生的思辨意识和理性精神方面也有其独特的作用，同时还能传播数学文化，激发学生的学习兴趣，值得数学教育者的深入研究和探讨，希望此文能引起同行更为深入的研究．