AsH+离子的电子结构和跃迁性质*

侯秋宇 关皓益 黄雨露 陈世林 杨明 万明杰

(宜宾学院理学部,宜宾 644007)

采用多参考组态相互作用方法计算了AsH+离子前3 个离解极限所对应的8 个电子态(X2Π,a4Σ-,A2Σ-,b4Π,B2Δ,C2Σ+,D2Π,22Σ+)的电子结构.As 原子选择了aug-cc-pwCV5Z-PP 相对论赝势基组.在计算中考虑了Davidson 修正,芯-价电子关联和自旋-轨道耦合效应.拟合得到了所有态的光谱常数,离解能越大的电子态,其谐振频率越大,平衡核间距越小.考虑自旋-轨道耦合效应后,由于避免交叉,B2Δ3/2 和B2Δ5/2 变为双势阱结构.最后预测了 A2Σ-→X2Π,→X2Π1/2和→X2Π1/2 跃迁的弗兰克-康登因子、自发辐射速率和自发辐射寿命,计算结果表明→X2Π1/2 阻禁跃迁的强度很小.本文的计算结果为以后AsH+离子的光谱实验研究提供理论基础.

1 引言

砷氢化物在半导体制造业扮演着重要的角色,为更好地得到其氢化物的性质,可以研究其分子离子的电子结构.1968 年,Dixon 等[1]首次利用闪光光解AsH3,观测到了AsH2在4000-5000 Å波长范围中的吸收光谱,对应的跃迁为2A1→2B1.1990 年,Arens 和Richter[2]观察到AsH 由b1Σ+到X3Σ-态的跃迁,并且测定了b1Σ+态的光谱常数.1996 年,Beutel 等[3]通过观察AsH 和AsD 的a1ΔX3Σ-红外发射光谱,确定了a1Δ 态精确的光谱常数.1986 年,Pettersson 和Langhoff[4]计算了AsH 分子基态的光谱常数和偶极矩,预测出AsH 氢化物在红外中具有很强的振动跃迁.之后Matsushita等[5]研究了关于AsH 低激发态的势能曲线和辐射寿 命.1989 年,Balasubramanian 和Nannegari[6]采用二次组态相互作用方法计算了AsH 分子16 个电子态的光谱常数和势能曲线,其中11 个态为束缚态.2009 年,施德恒等[7]采用耦合簇单双激发方法计算了AsH 分子势能曲线,并拟合得到了束缚态的光谱常数和分子常数.2022 年,边文生等[8]讨论了激光冷却AsH,SbH 和BiH 的可能性,计算结果表明AsH 和SbH 是激光冷却的候选分子.赵东风等[9]利用光腔衰荡光谱技术观察AsH2自由基,研究了在带的吸收光谱.

第五主族的氢化物正离子的势能曲线主要集中在NH+和PH+离子的研究上[10-14].2008 年,万明杰等[10]采用多组态准简并微扰理论(MCQDPT)方法计算了NH+离子的最低4 个电子态的电子结构.2015 年,杨传路等[11]采用多参考组态相互作用(MRCI)方法计算了2 个最低的2∏和2Σ+电子态的势能性质和跃迁性质,并预测了NH+离子是适合激光冷却的候选体系.1981 年,Bruna 等[12]采用MRCI 方法计算了PH+离子的势能曲线,并拟合得到了X2∏,4Σ-和2Δ 态的光谱常数.2008 年,Li 等[13]采用MCQDPT 方法计算了PH+离子X2∏和A2Δ态及其X2∏1/2,X2∏3/2,A2Δ3/2,A2Δ5/2态的势能曲线和光谱常数.2015 年,闫冰等[14]采用MRCI 方法计算了PH+离子的8 个Λ-S 态和15 个Ω 态的势能曲线.计算了A2Δ→X2∏和12Σ-→X2∏跃迁的弗兰克-康登因子,并预测了A2Δ 和12Σ-激发态的自发辐射寿命.国内也有很多学者研究了氢化物离子的电子结构,如AlH+,SeH+,SiH+等体系[15-17].

从以往的研究中可以看出,目前只有关于AsH分子的光谱性质和跃迁性质的理论和实验研究.本文拟在考虑自旋-轨道耦合(SOC)效应水平下研究AsH+离子的势能曲线、偶极矩和跃迁偶极矩,并拟合得到各束缚态的光谱常数和跃迁性质.

2 计算细节和方法

采用MOLPRO2010 程序[18]计算了AsH+离子的8 个Λ-S 态(X2Π,a4Σ-,A2Σ-,b4Π,B2Δ,C2Σ+,D2Π,22Σ+)的势能曲线.AsH+离子具有C∞V对称性,由于程序的限制,在计算中采用C2V子群计算了AsH+离子的电子结构.C2V子群有4 个不可约表示(A1,B1,B2,A2).电子态与不可约表示有相应的对应关系: A1↔Σ+,B1+B2↔Π,A1+A2↔Δ,A2↔Σ-.对H 原子选用了全电子aug-cc-pV5Z 基组[19],对As 原子选取了相对论赝势基组aug-ccpwCV5Z-PP[20].

在计算中采用Hartree-Fock 方法计算了AsH+离子的初始波函数;然后采用完全活性空间自洽场方法(CASSCF)[21,22]对AsH+离子的波函数进行优化.As 的3s 轨道为冻结轨道,As 的3p3d 轨道为双占据的闭壳层轨道,5 个分子轨道(3,1,1,0)作为活性空间,即As 的4s4p 和H 的1s 轨道,可以写为CAS(5,5).接着以优化后的波函数为参考,采用MRCI 方法[23,24],考虑Davidson 修正(+Q)[25]计算了8 个Λ-S 态的能量本征值.为提高计算的精度,As 的3p3d 电子用于考虑芯-价电子(CV)关联效应,即21 个电子参与了电子相关能的计算.最后在MRCI+Q水平下,通过Breit-Pauli 算符[26]来考虑SOC 效应.

采用LEVEL8.0 程序[27]通过求解径向薛定谔方程得到AsH+离子束缚态的平衡核间距Re、谐振频率ωe、非谐振频率ωeχe和离解能De以及 A2Σ-→X2Π ,→X2Π1/2和→X2Π1/2跃迁的弗兰克-康登因子、自发辐射速率和自发辐射寿命(τ).

3 结果与讨论

3.1 Λ-S 态的势能曲线与光谱常数

计算了AsH+离子的最低的三个离解极限所对应的8 个Λ-S 态的势能曲线,见图1,所计算的电子态均为束缚态.其中X2Π,a4Σ-,A2Σ-和b4Π 态对应最低离解极限As+(3Pg)+H(2Sg);B2Δ,C2Σ+和D2Π 态对应第二离解极限As+(1Dg)+H(2Sg);22Σ+态对应第三离解极限As+(1Sg)+H(2Sg).从图1可以看出,三个离解极限均为As++H,见表1.离解极限之间的相对能量与实验值符合较好[28].

图1 AsH+离子X2Π,a4Σ-,A2Σ-,b4Π,B2Δ,C2Σ+,D2Π和22Σ+态的势能曲线Fig.1.Potential energy curves of the X2Π,a4Σ-,A2Σ-,b4Π,B2Δ,C2Σ+,D2Π and 22Σ+ states of AsH+ cation.

表1 AsH+离子Λ-S 态的离解关系Table 1. Dissociation relationships of Λ-S states of AsH+.

所计算的8 个Λ-S 电子态的光谱常数列在表2中.在计算的8 个电子态中,离解能De越深的电子态,其谐振频率ωe越大,平衡核间距Re越小.AsH+离子的基态为X2Π,其离解能De和谐振频率ωe最大,分别达到了3.100 eV 和2222.58 cm-1,可以看出基态具有很强的稳定性;其平衡核间距Re为1.5131 Å,在Re处其主要电子组态为,占比达91.59%.a4Σ-态为第一激发态,其离解能为1.208 eV,也是一个比较强的束缚态;其位于基态15260.18 cm-1之上,在Re处的主要电子组态为,占比达90.4%.A2Σ-态为二重态的第一个激发态,和PH+离子一样,其离解能比较小,仅0.313 eV;其平衡核间距Re为2.0523 Å,在Re处的主要电子组态为,占比为87.63%.X2Π→A2Σ-跃迁主要是由 1σ→3π 的分子跃迁引起的.b4Π,C2Σ+和D2Π态的平衡核间距明显比其他电子态要大很多,并且离解能均小于0.05 eV 以及谐振频率都在100-200 cm-1,可以看出这三个态都是弱束缚态.其中b4Π 与22Σ+,C2Σ+和B2Δ 态的曲线分别在约1.70,2.15 和2.40 Å处相交,D2Π 与22Σ+态的曲线在约2.00 Å处相交,这也导致了考虑SOC效应时,AsH+离子的势能曲线很复杂.

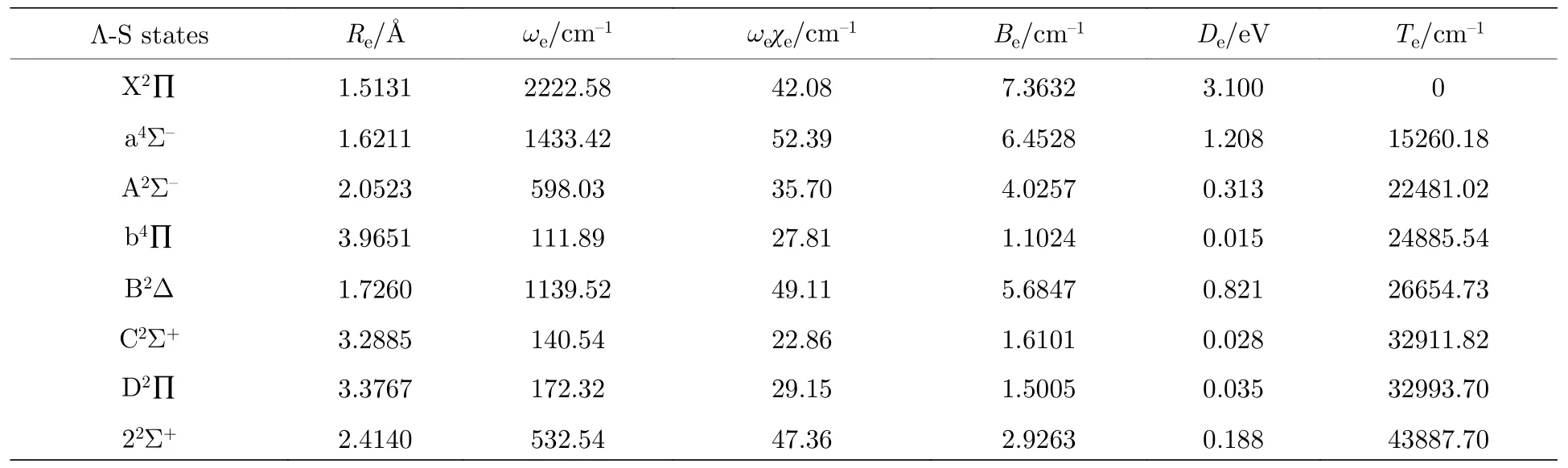
表2 Λ-S 的光谱常数Table 2. Spectroscopic parameters of the Λ-S states.

到目前为止,还缺少有关AsH+离子的势能曲线和光谱常数的研究.本文对比了同主族体系的实验值与理论值[10,14,29-31],见表3.从表3 可以看出,一方面,NH+,PH+和AsH+离子低电子态的能级顺序都是X2∏,a4Σ-,A2Σ-和B2Δ.NH+离子a4Σ-到X2∏态的垂直跃迁能非常小[31],仅有509 cm-1,而AsH+离子与PH+离子类似,其垂直跃迁能均超过了10000 cm-1;另一方面,随着M原子的核电荷数增加,MH+离子的平衡核间距增大,四个电子态的谐振频率ωe和离解能De减小.同时,由于 AsH+离子和GeH 和SnH 分子为等价电子体系,三个体系的最低4 个电子态的能级顺序也是相同的[32,33].

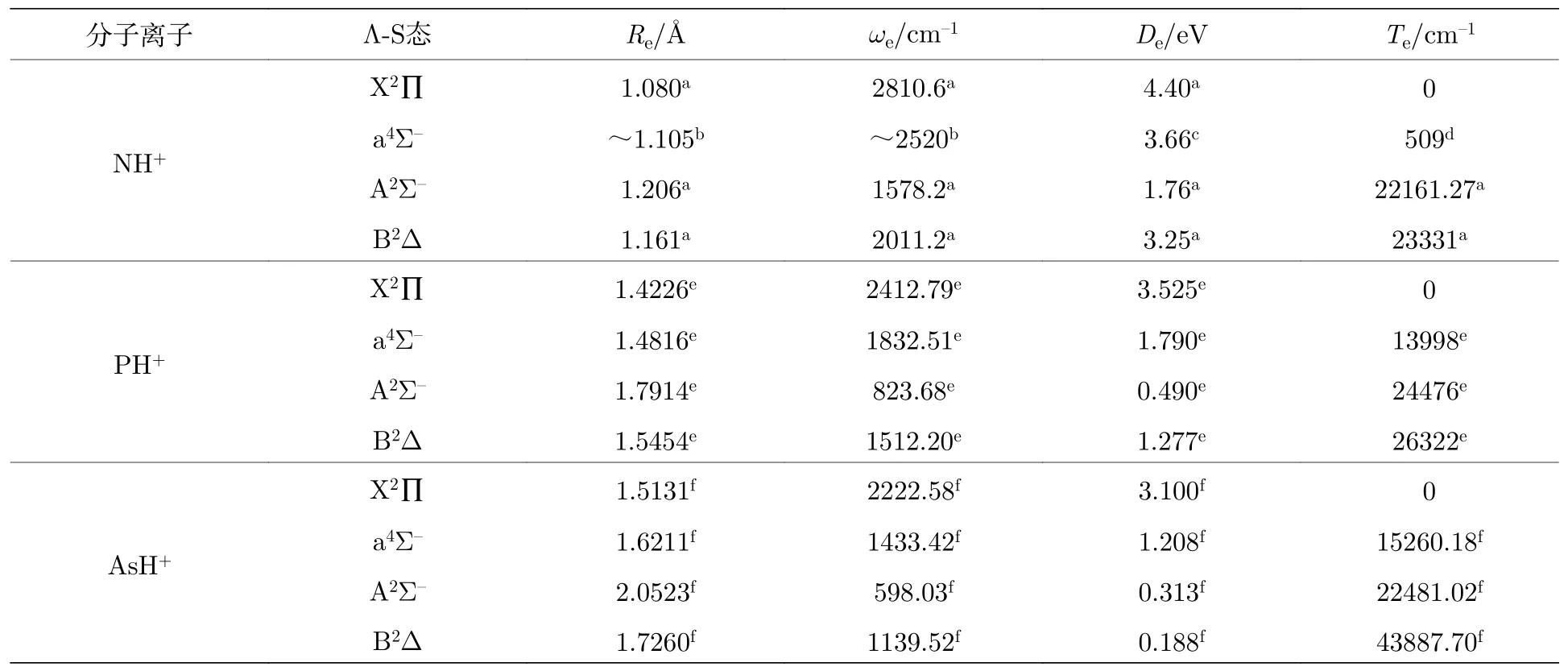
表3 第五主族氢化物离子的光谱常数对比Table 3. Comparison of the spectroscopy parameters of the Ⅴ-group hydride cations.

3.2 Ω 态的势能曲线与光谱常数

自旋-轨道耦合(SO)矩阵元的大小可以判断SOC 相互作用的强弱.激发态与基态之间的SO 矩阵元随核间距变化的曲线绘制在图2 中,

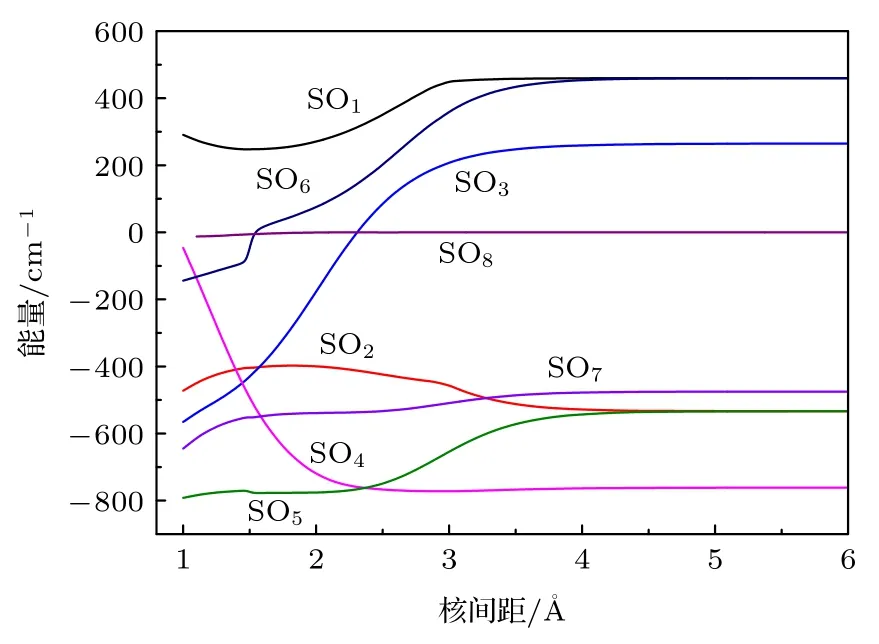
图2 电子态之间的自旋-轨道矩阵元.Fig.2.Spin-orbit matrix elements of the AsH+ anion.

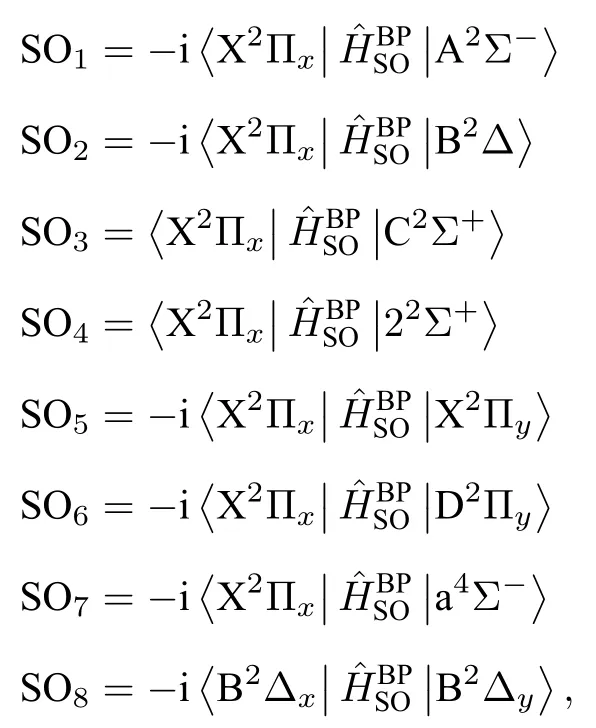
在考虑SOC 效应下计算了AsH+离子的电子结构.As+离子的3P 原子态分裂为3P0,1,2.故AsH+离子的离解极限增加至5 个,相应的8 个Λ-S 态分裂为15 个Ω 态,包括8 个1/2 态,5 个3/2 态和2 个5/2 态.基态的1/2 分量对应第一离解极限As+(3P0)+H(2S1/2),第二离解极限对应基态的3/2 分量和a4Σ-态与A2Σ-态的1/2 分量,第三离解极限对应a4Σ-态与B2Δ 态的3/2 分量,B2Δ 态的5/2 分量和C2Σ+与22Σ+态的1/2 分量.所对应的分子态与离解极限之间的能量差都列于表4 中.15 个Ω 态的势能曲线绘制于图3 中.部分Ω 态的光谱常数列于表5 中.

表4 AsH+离子Ω 态的离解关系Table 4. Dissociation relationships of Ω states of AsH+.

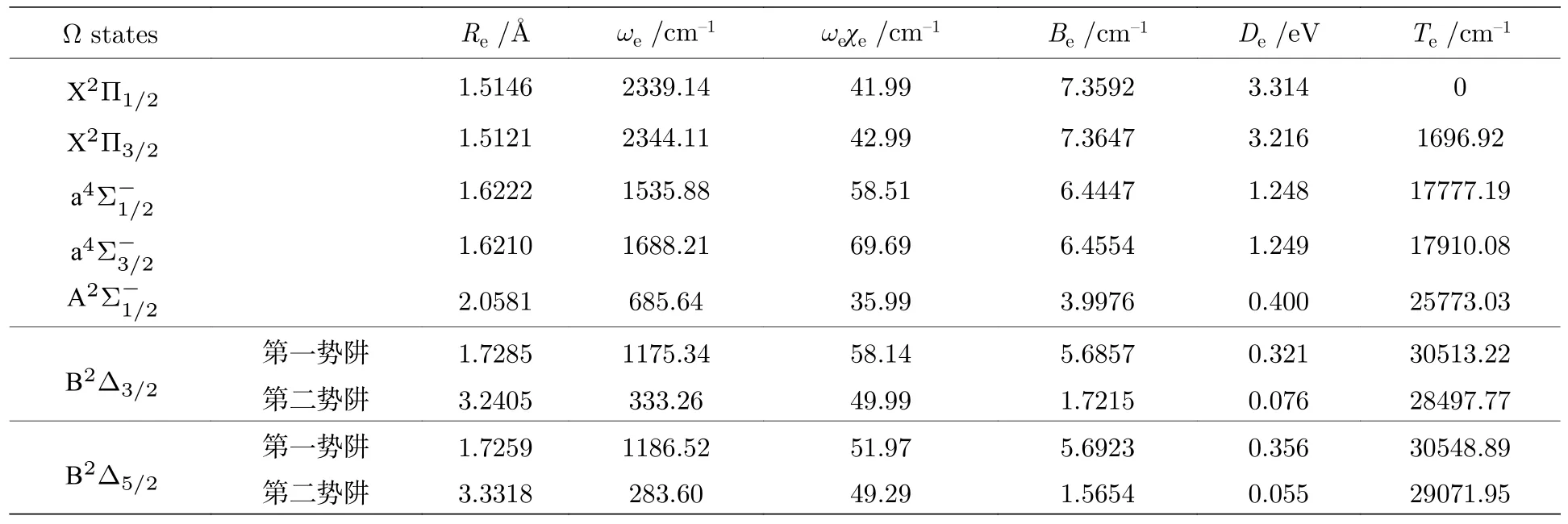
表5 Ω 的光谱常数Table 5. Spectroscopic parameters of the Ω states.

图3 Ω 态的势能曲线Fig.3.Potential energy curves of the Ω states of AsH+cation.

基态X2∏分裂为X2∏1/2和X2∏3/2态,其中X2∏1/2态的能量最低.对比分裂前后,离解能De有较大变化,分别增加0.214 eV 和0.116 eV.X2∏和a4Σ-态的分裂常数分别达到了1696.92 cm-1和132.89 cm-1,而PH+两个态的分裂常数分别只有294 cm-1和4 cm-1[14],说明了SOC 效应对AsH+离子的光谱常数影响很大.而B2Δ 态第一势阱的分裂常数仅为35.67 cm-1,原因是B2Δ 态两分量之间的SO 矩阵元几乎为零,所以B2Δ 态的分裂不明显.由于Λ-S 态的势能曲线有很多的相交现象,考虑SOC 效应后,当两个态的总角动量J相同时,自旋无关水平下曲线相交的两个态出现避免相交的情况.所以在30000-40000 cm-1能区,曲线出现了很多的避免交叉的现象,从而导致了部分电子态存在双势阱结构,如 B2Δ3/2和B2Δ5/2态均为双势阱结构,两个态分别与 b4Π3/2和b4Π5/2态在约2.36 Å处避免相交.

3.3 偶极矩、跃迁偶极矩、弗兰克-康登因子、自发辐射速率和自发辐射寿命

X2Π1/2,X2Π3/2,,B2Δ3/2,B2Δ5/2,b4Π3/2和b4Π5/2态的偶极矩绘制在图4 中.由于AsH+是正离子体系,所以所有的电子态在核间距逐渐增大(＞4 Å)时,偶极矩逐渐呈现增大的趋势.B2Δ3/2与b4Π3/2,B2Δ5/2与b4Π5/2存在明显的避免相交现象.X2Π1/2在平衡位置处的偶极矩为-0.3295 a.u.,比同电子体系GeH基态的偶极矩(0.026 a.u.)要大很多[32].可以说明离子体系的极性明显增强.

图4 Ω 态的偶极矩Fig.4.Dipole moments of the Ω states of AsH+ cation.

为了预测AsH+离子的跃迁性质,计算了 A2Σ-→X2Π,X2Π3/2→X2Π1/2,→X2Π1/2跃迁和→X2Π1/2阻禁跃迁的跃迁偶极矩,见图5.从图5 可以看出,X2Π3/2→X2Π1/2和→X2Π1/2跃迁的跃迁偶极矩都小于0.05 a.u.,由于 X2Π3/2,态来源于同一离解极限As+(3P1)+H(2S1/2),所以当核间距增大时,三个态到基态的跃迁偶极矩趋于同一极限.基态来源于As+(3P0)+H(2S1/2),而As+离子3P1和3P0同为其基态3P 的分裂态,可以看出3P1→3P0能级跃迁的跃迁偶极矩大约为零.

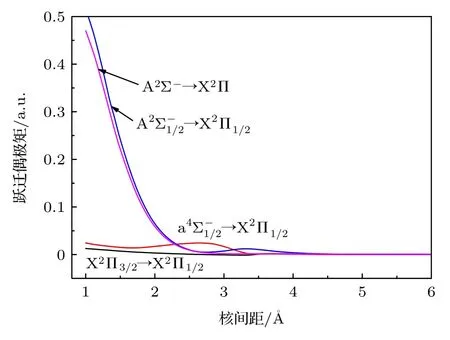
图5 AsH+离子的跃迁偶极矩Fig.5.Transition dipole moments of AsH+ cation.

基于精确的势能曲线和跃迁偶极矩,计算了A2Σ-→X2Π,→X2Π1/2和→X2Π1/2跃迁的跃迁性质,限于篇幅,各跃迁只列了ν＇=0前6 个振动能级的弗兰克-康登因子、自发辐射速率和自发辐射寿命,列于表6 中.由于与X2Π1/2态的平衡核间距更接近,所以→X2Π1/2跃迁的弗兰克-康登因子f00比→X2Π1/2跃迁的要大很多,也说明了振动态的波函数与 X2Π1/2振动态的波函数重叠程度更大.Li 等[32]计算了等电子体系GeH 的激发态的自发辐射寿命,仅为200 µs.本文预测得到AsH+离子的激发态的自发辐射寿命为517 µs.说明了这两个体系的→X2Π1/2阻禁跃迁的强度都很小.

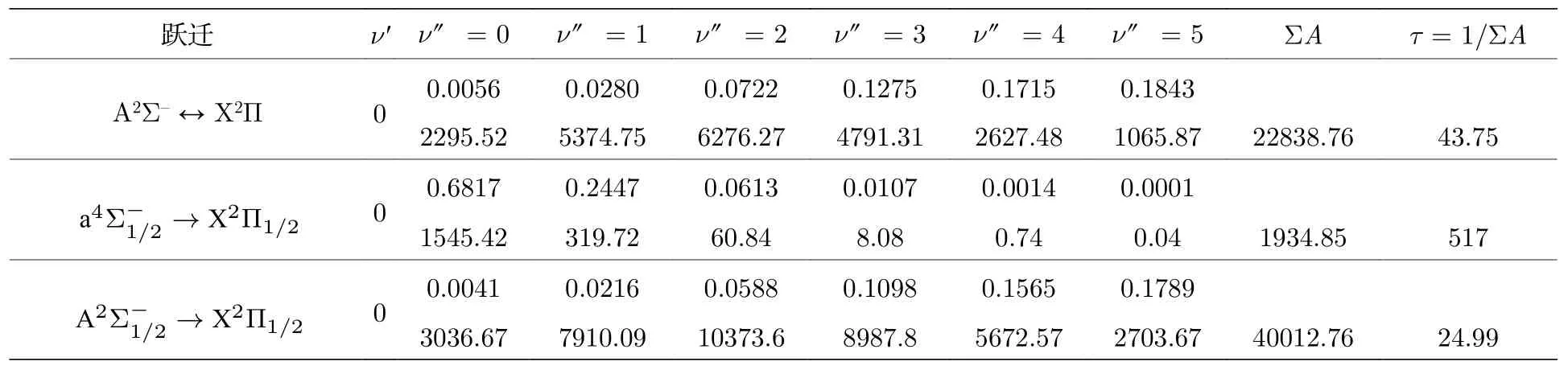
表6 AsH+离子的弗兰克-康登因子(单位: s-1)、总自发辐射速率和自发辐射寿命(单位: µs)Table 6. Franck-Condon Factors,spontaneous emission rates(unit of s-1)and spontaneous radiative lifetimes τ(unit of µs)of the AsH+ cation.

4 结论

本文采用MRCI+Q方法,并考虑了CV 电子关联效应分别计算了自旋无关和考虑自旋-轨道耦合效应下AsH+离子的基态和低激发态的势能曲线、偶极矩和跃迁偶极矩.结果表明本文计算的所有电子态都是束缚态,X2Π 态为基态,而b4Π,C2Σ+和D2Π 态为弱束缚态.通过求解径向薛定谔方程,计算得到了其光谱常数和跃迁性质.由于没有实验值和其他理论值,本文与同主族氢化物离子的电子态的光谱常数进行了对比,NH+,PH+和AsH+离子低电子态的能级顺序相同,随着同主簇原子的核电荷数M的增加,MH+离子的平衡核间距增大,谐振频率ωe和离解能De减小.b4Π 和B2Δ 态的势能曲线相交,在考虑SOC 效应后,遵循避免交叉原则,B2Δ3/2和B2Δ5/2态均产生了双势阱结构.最后预测了 A2Σ-→X2Π,→X2Π1/2和→X2Π1/2跃迁的弗兰克-康登因子、自发辐射速率和自发辐射寿命,计算结果表明态的自发辐射寿命为517 µs,→X2Π1/2阻禁跃迁的强度很小.