基于改进自抗扰的电压控制型双馈风电机组故障穿越策略
谢 震,崔 建,李 喆,张 兴
(合肥工业大学电气与自动化工程学院,安徽省合肥市 230009)
0 引言
随着可再生能源的发展,风力发电也得到了快速发展,其中以双馈感应发电机(doubly-fed induction generator,DFIG)为基础的风力发电系统因其出色的特性得到广泛研究和应用[1]。从定向角度可将DFIG 机侧控制模式分为电流控制型和电压控制型,二者因并网方式不同,在弱电网下呈现不同的并网特性[2-4]。在弱电网下,电流控制型DFIG 由于锁相环与电流控制耦合,控制性能会发生恶化,而电压控制型DFIG(VC-DFIG)采用自同步并网方式,不依赖于锁相环,因此避免了上述影响[5-6]。
电压控制型双馈风电机组的功率外环采用自同步的并网方式,更适合在弱电网下运行。对于虚拟同步发电机(virtual synchronous generator,VSG)控制下的DFIG,近年来有不少相关研究[7-12]。文献[7]针对VSG 控制下的DFIG 并网时存在功率耦合的问题,结合自适应虚拟阻抗策略实现功率解耦。文献[8]针对VSG 控制下的DFIG 存在小扰动稳定性问题,通过阻抗建模对其稳定性进行分析,提出可通过适当增大虚拟惯量时间常数和阻抗系数提高其并网稳定性。文献[9]研究了VSG 控制下的DFIG在弱电网下的运行能力,通过特征值分析和仿真得出其在弱电网下具有较好的稳定性和频率支撑能力。
上述文献仅对VC-DFIG 在正常电网中的控制进行了研究。对于电网故障下电磁暂态引起的转子过流问题,如果没有相应的保护措施或控制方案,可能会对电机的正常运行造成影响,甚至损坏转子侧变流器[13]。针对故障下的电磁暂态问题,目前已有较多文献提出了针对电流控制型DFIG 的故障穿越控制策略[14-19],但对于VC-DFIG 电网故障暂态问题的研究还较少。文献[20-21]针对VSG 控制下的DFIG故障电流问题,提出将虚拟电阻和限流相结合,保证了VSG 在电网对称故障下的正常工作。文献[22]针对VSG 控制下的DFIG 在电网故障下暂态分量失控的问题,提出在VSG 中增加气隙磁通反馈并结合相应的限流策略,保证了VSG 控制下的DFIG 在故障期间能够正常工作,也加速了暂态分量的衰减。文献[23-24]针对虚拟同步控制策略下DFIG在电网对称故障时存在的转子过流问题,提出在转子电压处补偿一定的暂态分量,有效抑制了转子过电流,但是所提策略依赖于模型的准确性,鲁棒性较差。
针对VC-DFIG 在电网对称故障下的转子过电流问题,可通过抑制引起转子过电流的扰动来解决。对于扰动的抑制问题,文献[25]基于比例-积分-微分(PID)的控制思想提出自抗扰控制(active disturbance rejection control,ADRC),其由3 个部分组成:跟踪微分器、非线性反馈和扩张状态观测器(extended state observer,ESO)。ESO 是ADRC 的核心部分,其通过输出信息对扰动进行主动估计和补偿,从而达到消除扰动的目的[26]。文献[27]针对永磁同步电机中存在负载转矩和参数变化的扰动问题,提出基于ADRC 的位置-电流双闭环策略,有效减小了负载转矩和参数变化对电机性能的影响,但是其针对的扰动是小范围的恒定扰动。目前,有关ADRC 应用于双馈风电机组的研究还比较少,针对VC-DFIG 电网对称故障下的ADRC 扰动估计和补偿能力还不清楚,有必要对其进行研究。
本文首先介绍了VC-DFIG 的控制结构,对其在电网对称故障下的转子侧电压进行分析,得出故障下引起转子过电流的主要扰动。然后,针对故障下的转子过流问题,分析现有暂态补偿策略及其不足,提出基于改进自抗扰的转子电流控制方案。最后,对控制系统进行稳定性分析,通过实验平台验证所提策略的优越性。
1 VC-DFIG 控制结构
本文研究的VC-DFIG 控制结构如图1 所示。其中,控制环节分为2 个部分:功率外环和定子电压环、转子电流内环。功率外环输出同步角速度和电压幅值,定子电压环和转子电流环使得VC-DFIG具有控制电压和电流的能力[7]。
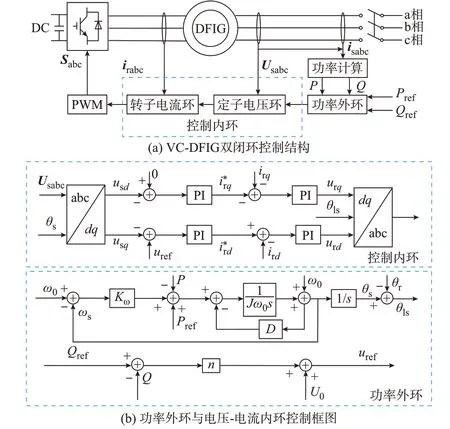
图1 VC-DFIG 控制结构Fig.1 Control structure of VC-DFIG


2 电网对称故障下VC-DFIG 的转子侧电压分析
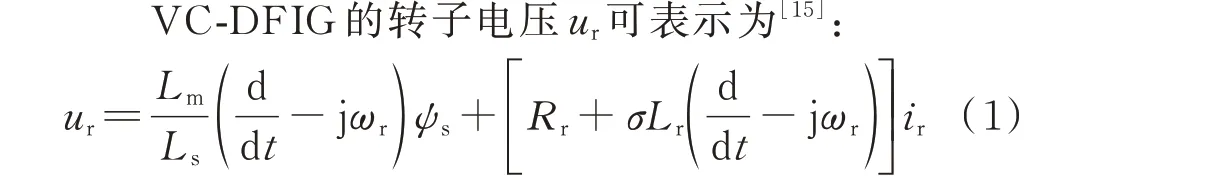
式中:Ls、Lr、Lm分别为定子电感、转子电感和互感;ψs为定子磁链;ωr为转子角速度;Rr为转子电阻;ir为转子电流;σ为漏磁系数且σ=1-L2m/(LsLr)。
式(1)等号右边的第1 项为反电动势er(见式(2)),与定子磁链有关;第2 项为转子回路的阻抗压降。
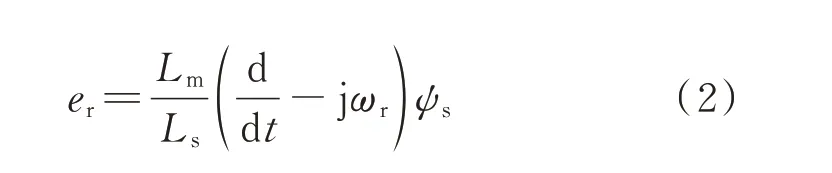
假设系统在t=0 时发生电网对称跌落,跌落深度为p,故障前VC-DFIG 的稳定运行电压为V,可得[23]:
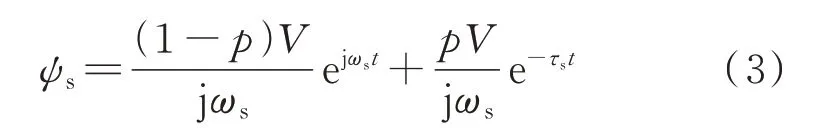
式中:τs=Ls/Rs为时间常数,其中Rs为定子电阻。
式(3)等号右边第1 项为故障下定子的稳态磁链Ψsf,与故障期间的稳态电压有关;第2 项为故障下定子的暂态磁链Ψst,可以使故障瞬间定子磁链保持连续。故障期间,定子的稳态磁链和暂态磁链都会在转子侧感应出对应的反电动势erf和ert:
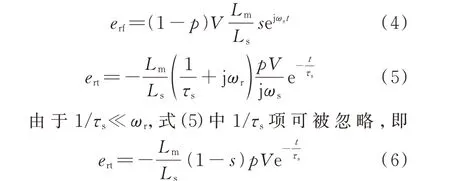
因为转差率s受转子侧变流器容量的影响,一般在-0.3~0.3 范围内变化,对比式(4)和式(6)可知,故障下转子开路电压中ert为主要部分,此时VCDFIG 的转子电压、电流满足:
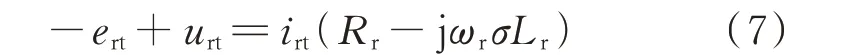
式中:urt为暂态电压;irt为暂态电流。
故障下因控制环节无法在短时间内做出响应,无法产生对应的暂态电压,即urt=0。由式(7)可知,此时ert直接作用于转子回路的阻抗上,因回路阻抗一般比较小,将会产生较大的转子过电流。
3 VC-DFIG 的故障穿越策略
3.1 基于暂态补偿的控制策略
由上述分析可知,转子过电流是由定子暂态磁链在转子回路感应出的暂态反电动势所导致的,可在转子电压指令值上补偿一定的暂态分量来减小转子电流冲击。暂态磁链Ψst可由全磁链Ψs和稳态磁链Ψsf获得,其表示如下:

式中:k为补偿系 数。当k=1 时,urn=ert,ert得到完全补偿;当k<1 时,ert得到欠补偿;当k>1 时,ert得到过补偿。
由暂态补偿量urt的表达式可看出,其与补偿系数、电机参数以及电网状态有关。由于其直接补偿在转子电压上,如果补偿系数、电机模型或参数发生变化,会对补偿效果造成影响,甚至可能会影响原控制系统的稳定性,导致鲁棒性较差。
3.2 基于改进ADRC 的控制策略
由上述分析可知,暂态补偿策略的补偿效果受到多方面因素的影响,存在不确定性。关于扰动抑制问题,文献[25]提出了一种新型控制结构,即ADRC。
3.2.1 ADRC 工作原理
对于一个控制系统来说,如果某一扰动对输出造成影响,其作用将会通过输出信息反映出来。ADRC 工作核心将系统标准型之外的因素视为一个总扰动,通过ESO 在输出信息中对扰动估计并补偿。设计ESO 的步骤一般如下。
以一阶系统为例,其可表示为:
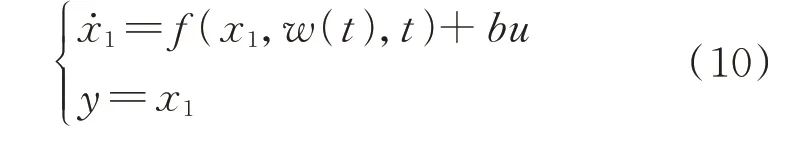
式中:x1为系统的状态量;b为系统参数;u为控制输入量;y为控制输出量;w(t)为外部扰动作用;f(x1,w(t),t)为总和扰动,其包括建模和未建模、外部扰动,将其扩张为新的状态变量x2=f(x1,w(t),t)。

式中:fal(e1,α1,δ1)为非线性函数;b0为控制放大系数,可 由 系 统 模 型 参 数 获 取;x̂1和x̂2分 别 为 输 出 量和扰动量的估计值;β1和β2为观测器增益系数;α1、α2、α为非线性因子,其取值一般小于1;δ1、δ2、δ为线性段间隔长度,其取值一般小于0.1。
3.2.2 基于ADRC 的转子电流环设计
同步旋转坐标系下的转子电流d、q轴分量如下[7]:
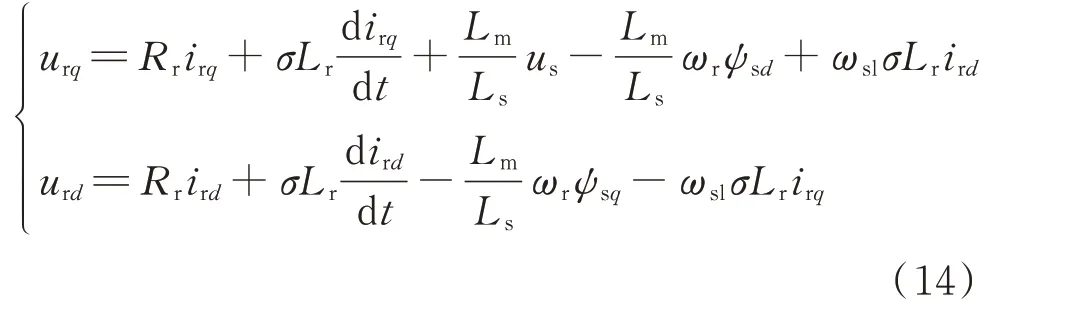
式中:ψsd和ψsq分别为定子磁链的d、q轴分量;ωsl为转差角频率且ωsl=ωs-ωr。
对式(14)的输入、输出线性化可得:
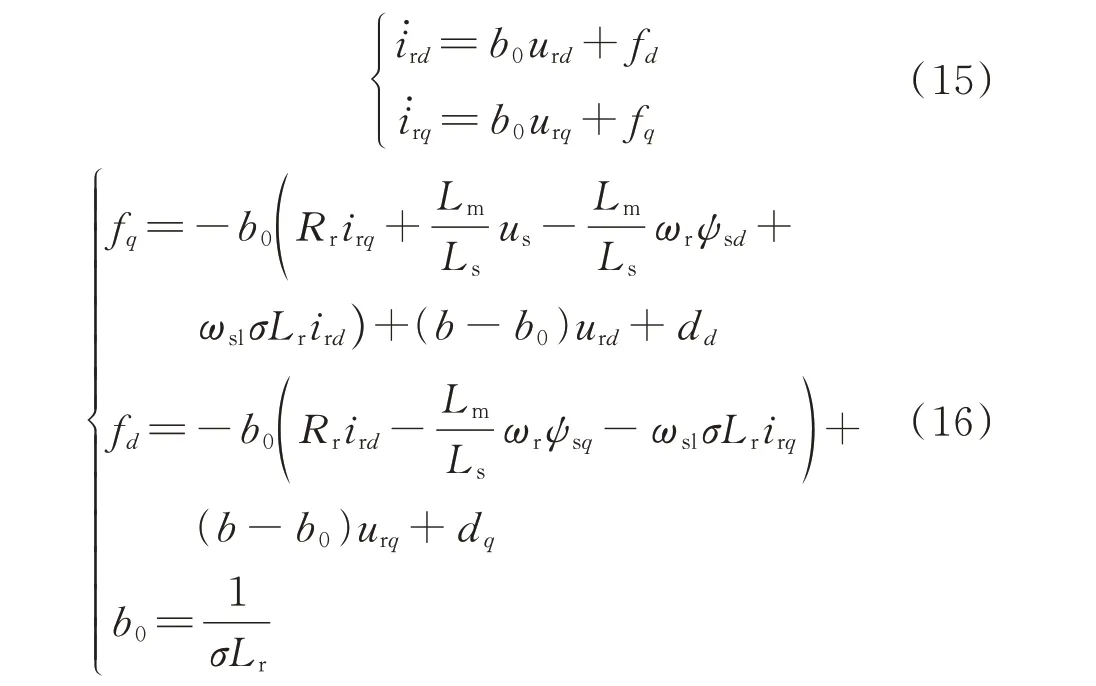
式中:dd和dq分别为d、q轴未知扰动,其主要为作用于被控量但未在模型中表示的扰动,如参数变化引起的扰动;fd和fq分别为d、q轴总扰动,模型主要由阻抗压降、定子电压、定子磁链、两回路的耦合量、参数误差引起的扰动、未知扰动构成。
上述转子电流控制环路的控制输入量为转子电压ur,输出量为转子电流ir,相对阶数为一阶。为估计总扰动fd和fq,将总扰动扩张为新的状态变量,设计的二阶ESO 如下:
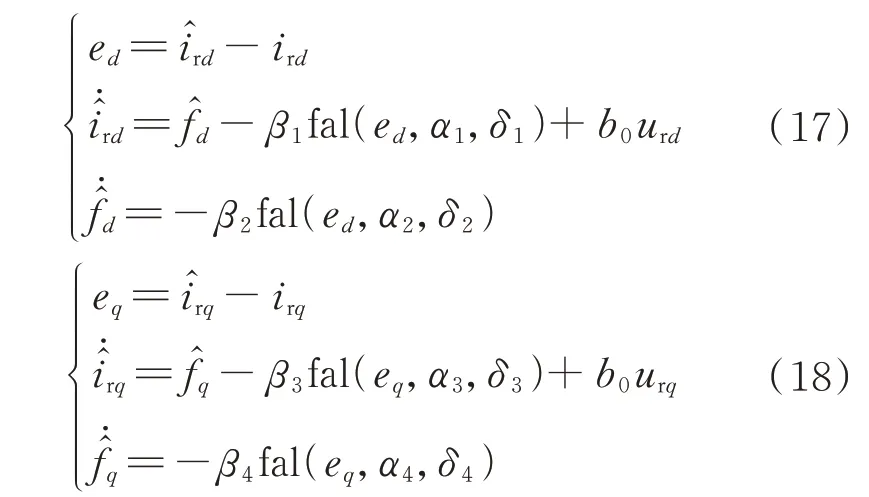
式 中:îrd、îrq和f̂d、f̂q分 别 为 转 子 电 流 和 扰 动 量 观 测 值的d、q轴分量;ed和eq分别为输出量转子电流观测值与反馈值误差的d、q轴分量;α3和α4为非线性因子;β3和β4为观测器增益,其值的选取主要依据带宽和经验整定法;δ3和δ4为线性段间隔长度。
若扰动估计准确,系统将变为简单的一阶积分型串联系统,其状态误差反馈控制律可设计如下:
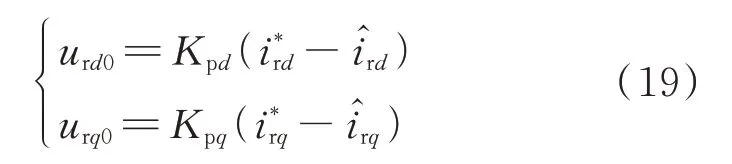
式中:urd0和urq0分别为对应转子d、q轴状态误差反馈控制律;Kpd和Kpq分别为d、q轴控制器增益。则其控制量如式(20)所示。

但是对于电网对称故障引起的短时间内工频衰减振荡的大扰动,ESO 可能存在扰动估计能力不足的问题,难以对扰动进行有效的估计和补偿。由式(21)可知,此时扰动的估计值和实际扰动值偏差较大,由扰动引起的转子电流也不能较好地抑制。
3.2.3 改进ADRC 的控制策略
为改进常规ADRC 存在电网对称故障下扰动估计补偿不足的问题,将由定子磁链模型获取的暂态分量作为已知扰动引入扰动估计,则式(15)重新表示为:
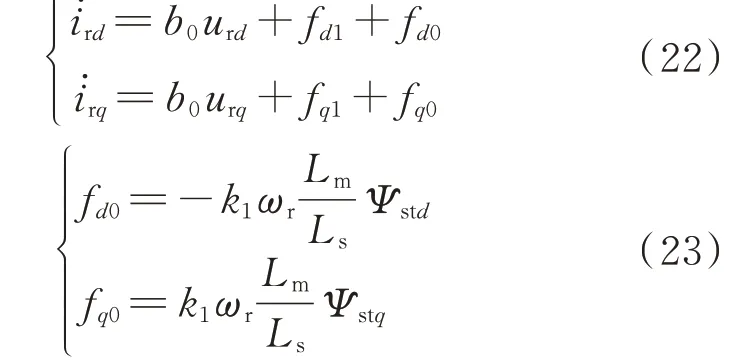
式中:fd1和fq1分别为由ESO 根据输出反馈所估计的扰动的d、q轴分量;fd0和fq0分别为由定子磁链获取的d、q轴暂态分量,其作为固定扰动加入扰动补偿中;k1为补偿系数,其选取原则与暂态补偿策略一致;Ψstd和Ψstq分别为暂态磁链的d、q轴分量。
将扰动项fd1和fq1视为新的状态量,可将式(22)重新表述如下:
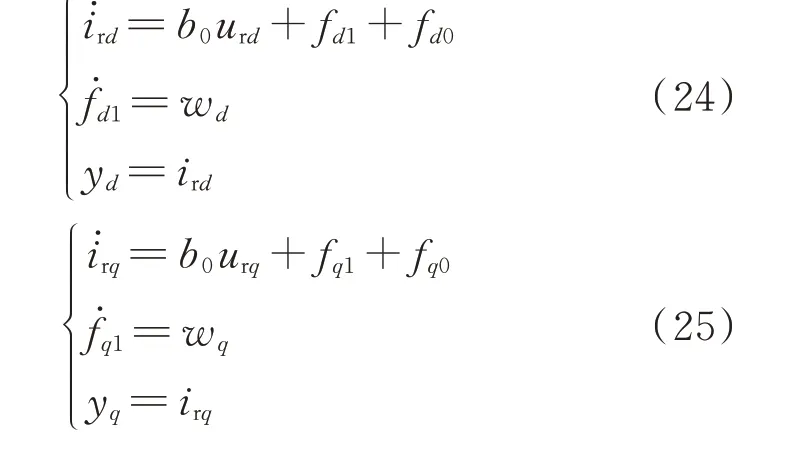
式中:wd和wq分别为d、q轴有界函数;yd和yq分别为d、q轴输出量。
为对扰动fd1和fq1进行观测,设计二阶ESO 如下:
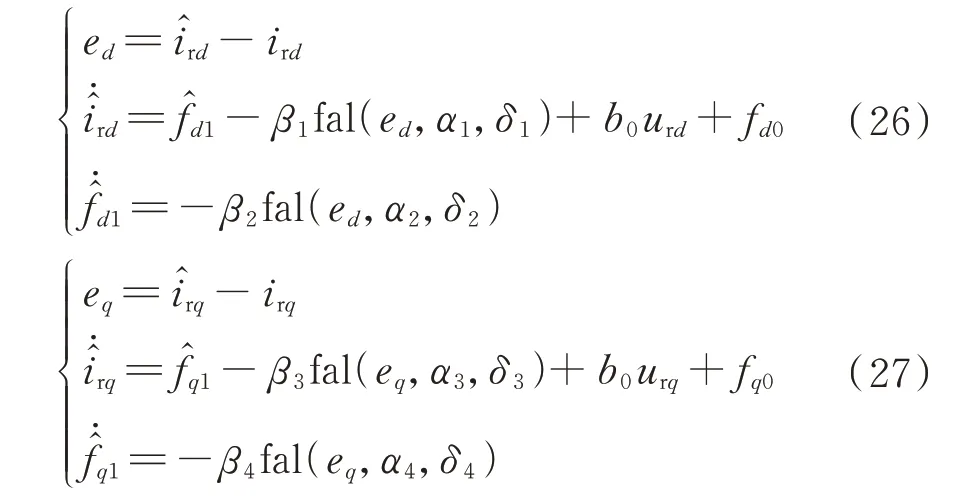
式 中:f̂d1和f̂q1分 别 为 剩 余 未 被 补 偿 扰 动 的 观 测 值 的d、q轴分量。
改进ADRC 控制策略下,由式(20)、式(22)可知控制器输入设计为如下形式:
如式(29)所示,电网对称故障瞬间,扰动补偿量 从f̂d变 为f̂d1+fd0,扰 动 补 偿 速 度 变 快,扰 动 补 偿量与实际扰动量的偏差由原先的fd-f̂d变为fdf̂d1-fd0,所提改进策略进一步减小了扰动补偿量与实际扰动量的偏差,转子过电流得到进一步的抑制。
由上述分析可知,常规ADRC 本身具有一定扰动抑制能力。假设当暂态分量fd0和fq0因电机模型或参数变大时,增大量为fd01和fq01,则式(22)变为:
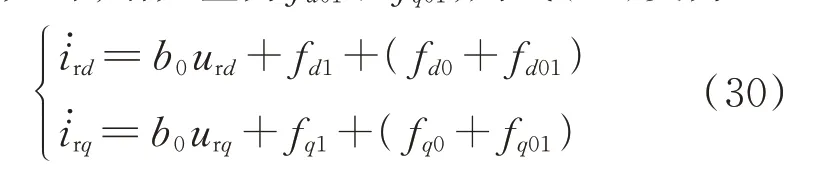
若这部分变化引起输出量的变化,ESO 能够从输 出 信 息 中 提 取 相 应 的 扰 动 量f̂d01和f̂q01,将 式(28)代入式(30)可得此时转子电流的表达式如下:
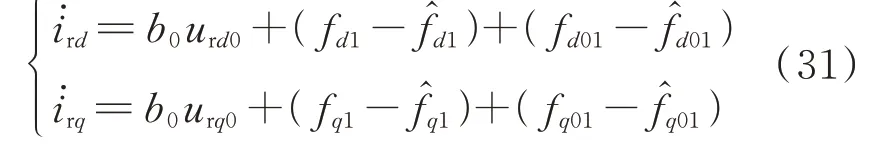
由式(31)可知,ESO 能够抑制因电机参数或模型导致暂态分量偏差所引起的扰动,降低其对系统的影响。由式(26)至式(28)可得基于改进ADRC的控制框图如图2 所示。
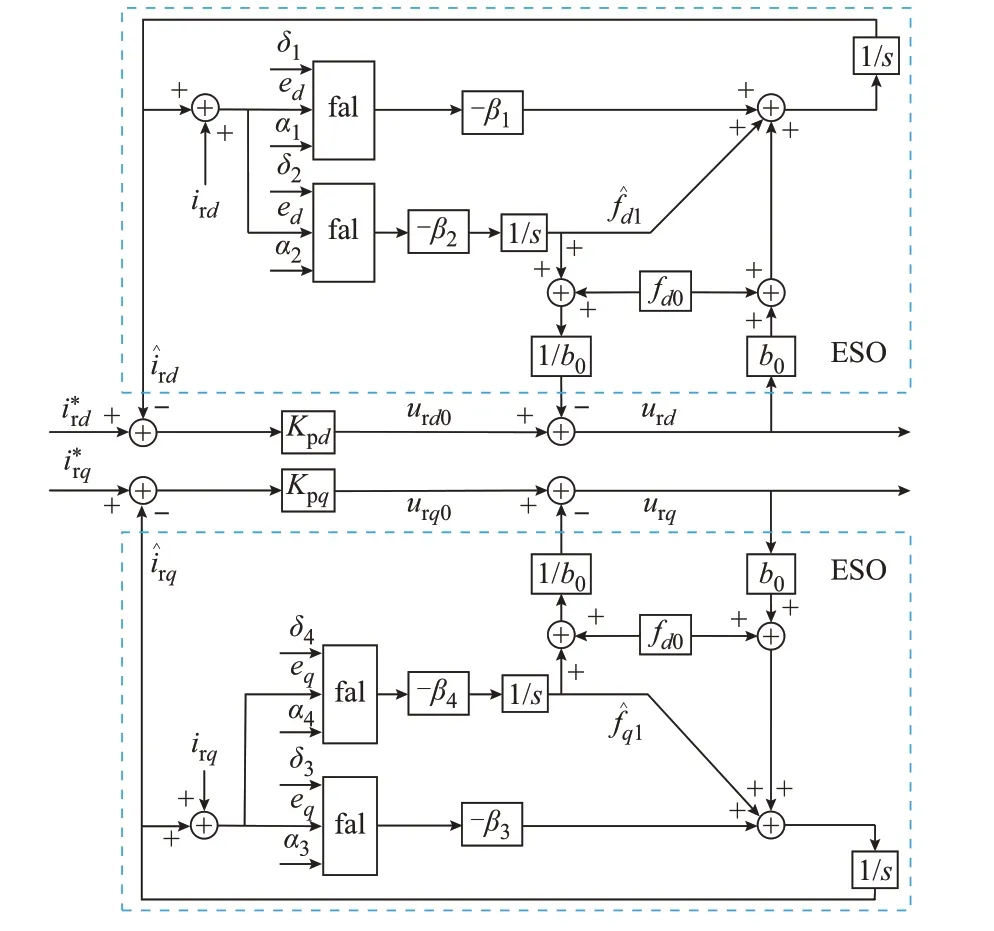
图2 基于改进ADRC 的控制策略框图Fig.2 Block diagram of control strategy based on improved ADRC
4 稳定性分析
因d轴与q轴是对称且互相独立的,只需对其中一轴的稳定性进行分析即可,以下主要针对d轴的稳定性进行分析。
4.1 ESO 稳定性分析
对fal(ed,α1,δ1)和fal(ed,α2,δ2)做适当变化可得:
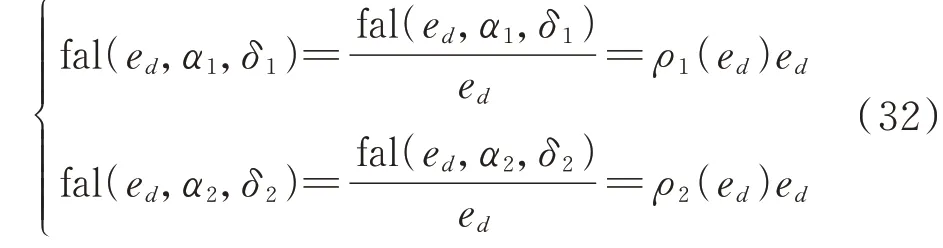
式中:ρ1(ed)和ρ2(ed)为误差缩放系数,跟随误差变化。
选取α1=α2、δ1=δ2,则定义:

根据式(36)可知0 <ρ(ed)<4.47,β1ρ(ed)和β2ρ(ed)是在一定范围内变化的函数,可根据劳斯判据方法对其进行稳定性分析[28]。
根据式(35)可得其特征方程为s2+β1ρ(ed)s+β2ρ(ed)=0,列出其劳斯表,详见附录A。由劳斯判据可得ESO 的稳定条件为:

由于ESO 观测器带宽的值均为正,即ρ(ed)>0,故ESO 是稳定的。
4.2 系统稳定性分析
由式(22)和式(30)可得d轴控制系统表达式为:

式 中 :Δ=s3+β1ρs2+(2β2ρ+b0β1ρKpd)s+b0β2ρKpd,其中ρ=ρ(ed)。
由 式(39)可 得 其 特 征 方 程 为s3+β1ρs2+(2β2ρ+b0β1ρKpd)s+b0β2ρKpd=0,列 出 其 劳 斯表,详见附录A。由劳斯判据可得系统稳定性条件为:

当系统进入稳态时,式(41)中等号右边全收敛为零,则有:
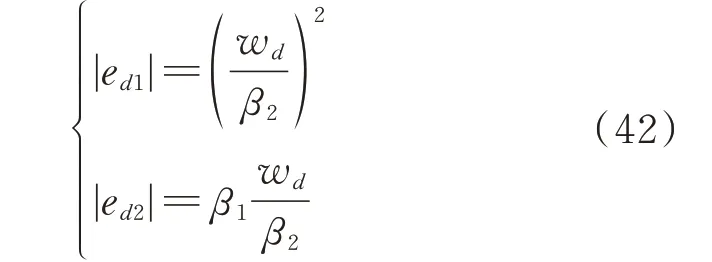
当β2远大于wd时,ESO 的观测误差会足够小,这时有|ed1|<1,1 <ρ(ed)<4.47。由此可得:
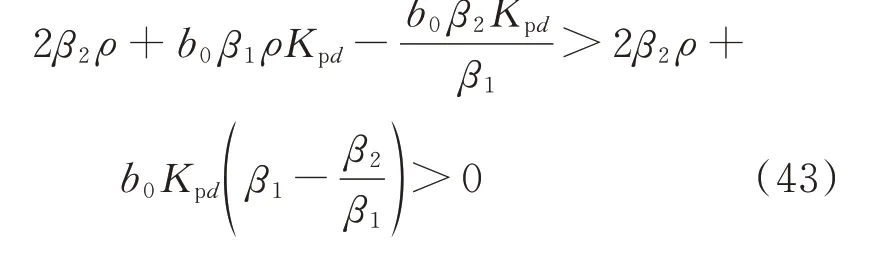
由式(40)和式(43)可知,d轴闭环控制系统是稳定的。同理,q轴也是稳定的。
5 实验验证
为验证所提策略的优越性,在11 kW 双馈风电机组实验平台上进行实验验证,实验平台相关实物图如附录B 图B1 所示。
实验平台所用的DFIG 参数如表1 所示。在某一时刻,电网电压发生对称跌落,跌落深度为50%,持续时间为500 ms。本次实验对电机运行在次同步和超同步2 种工况下的实验结果进行分析,实验波形如图3 所示,具体实验数据对比见附录B。
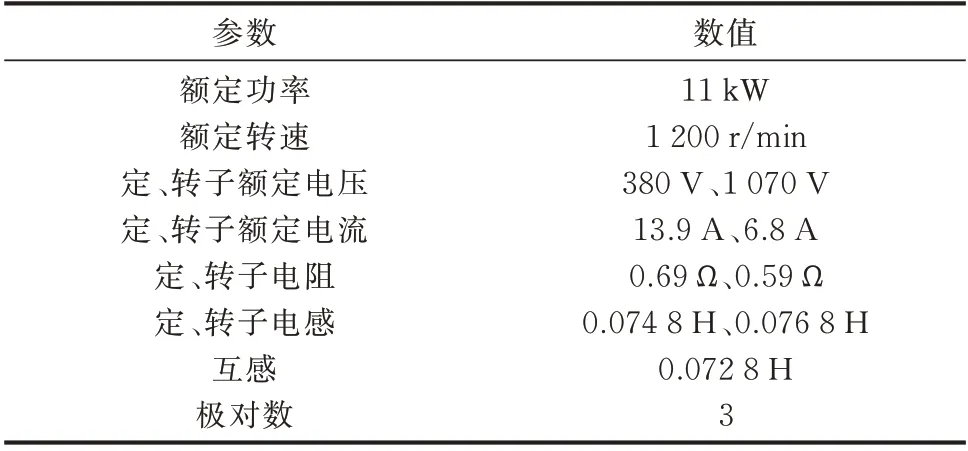
表1 DFIG 参数Table 1 Parameters of DFIG
1)次同步工况(转速为900 r/min)
电网对称故障前,有功功率给定为0.4 p.u.,无功功率给定为0.18 p.u.。图3(a)为无策略加入下的VC-DFIG 实验波形。从图中可以看出,电网电压跌落期间的最大转子冲击电流约为12.6 A,转子过电流为9 A,电磁转矩波振荡幅度约为0.27~0.45 p.u.。图3(b)为 常 规ADRC 策 略 下 的VC-DFIG 实 验 波形。从图中可以看出,故障瞬间转子最大冲击电流约为8.6 A,过电流抑制比约为44%,电磁转矩振荡幅度降到0.304~0.396 p.u.,有功、无功故障下的振荡也得到一定抑制,说明该策略具有一定的转子过电流抑制能力。图3(c)为基于暂态补偿的VCDFIG 实验波形。从图中可以看出,故障瞬间转子最大冲击电流降至6.5 A,转子过电流抑制比约为67.7%,暂态衰减时间约为210 ms,电磁转矩振荡范围缩小至0.31~0.38 p.u.,对有功、无功功率在故障期间的振荡抑制更加明显。对比图3(a)和(c)可知,转子电压故障期间的稳态脉动是由暂态补偿量引起的。图3(d)为本文所提改进ADRC 策略下的VCDFIG 实验波形。从图中可以看出,故障瞬间的转子最大冲击电流降至5.4 A,转子过电流抑制比约为80%,暂态衰减时间约为170 ms,电磁转矩振荡范围降至0.31~0.37 p.u.。对比图3(b)和(c)可发现,所提策略进一步抑制转子过电流的同时也加快了暂态衰减速度。对比图3(c)和(d)故障期间的转子电压可发现,所提策略控制下的转子电压几乎没有稳态脉动现象,能有效抑制暂态分量变化带来的扰动,体现了所提策略良好的鲁棒性。图3(e)为电感失配20% 时改进ADRC 策略下的VC-DFIG 实验波形。当Lm减小时,故障下的暂态分量会随之变小,此时故障瞬间转子最大冲击电流为5.8 A,转子过电流抑制比约为75%,暂态衰减时间约为180 ms,电磁转矩波动范围变为0.310~0.375 p.u.,其与图3(d)的实验结果接近。实验结果对比说明,改进ADRC 策略对暂态磁链依赖度较低,具有良好的鲁棒性。
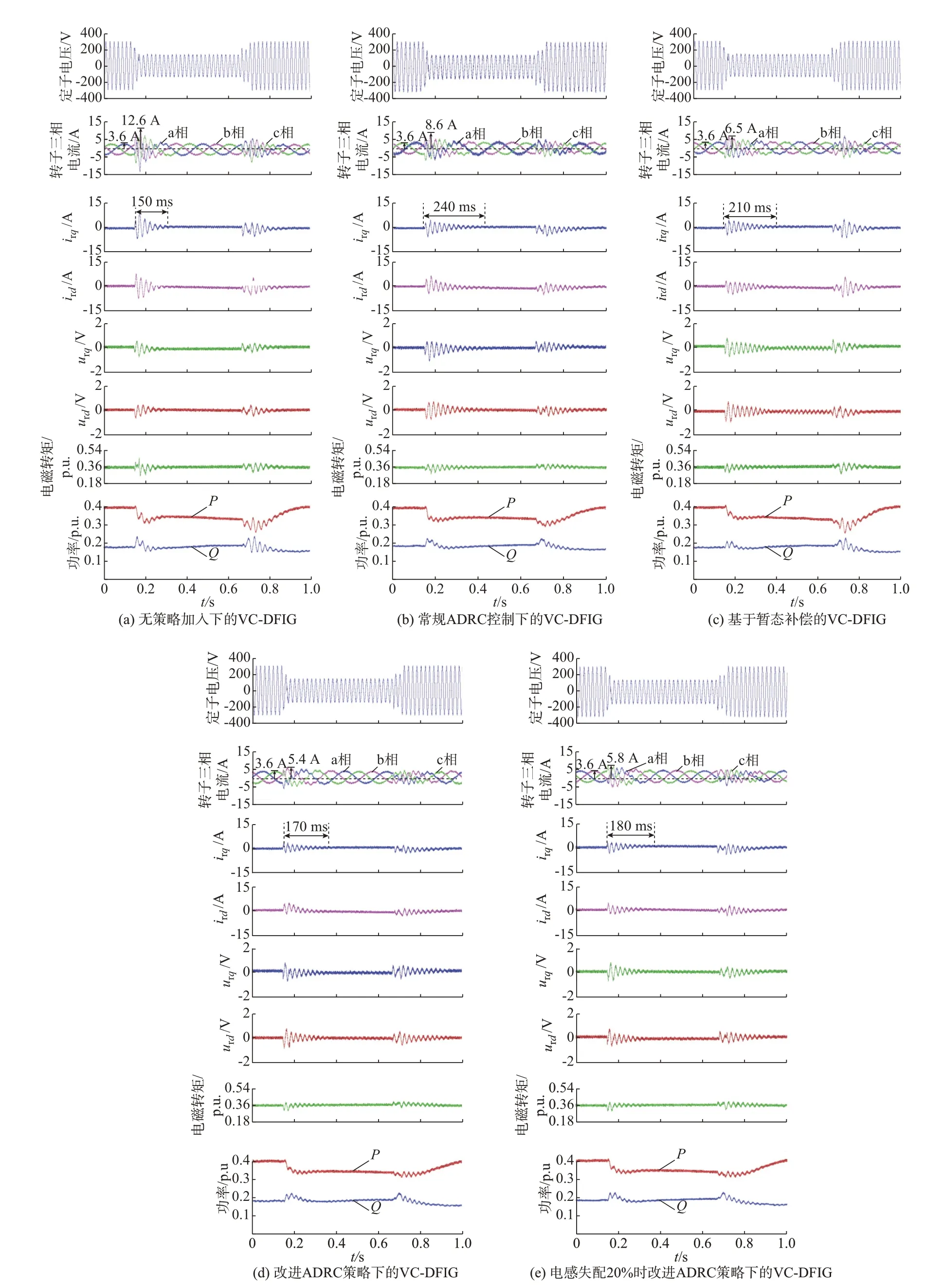
图3 次同步50%电网电压对称跌落下的实验结果Fig.3 Experimental results of sub-synchronous 50% symmetric drop of grid voltage
2)超同步工况(转速为1 050 r/min)
图4(a)至(c)分别为超同步工况无策略加入下的VC-DFIG、基于暂态补偿的VC-DFIG 和本文所提控制策略的VC-DFIG 实验波形图。由图4(a)可以看出,电网对称故障瞬间转子最大冲击电流为12.6 A,电磁转矩振荡范围为0.26~0.44 p.u.。由图4(b)可以看出,故障瞬间转子最大冲击电流降至6.3 A,转子过电流抑制比约为70%,暂态衰减时间为190 ms,电磁转矩振荡区间为0.31~0.38 p.u.,转子电压在故障期间也存在稳态脉动现象。由图4(c)可以看出,其故障瞬间转子最大冲击电流降低至5.5 A,转子过电流抑制比约为78%,暂态衰减时间约为160 ms,电磁转矩振荡区间进一步缩小为0.32~0.38 p.u.,转子电压在故障期间几乎无脉动现象发生,有功、无功功率在故障瞬间的振荡也得到进一步抑制。对比图4(b)和(c)可知,所提策略能进一步抑制转子过电流,同时缩短快暂态衰减时间,与次同步工况下得出结论一致,验证了改进ADRC 控制策略的优越性。
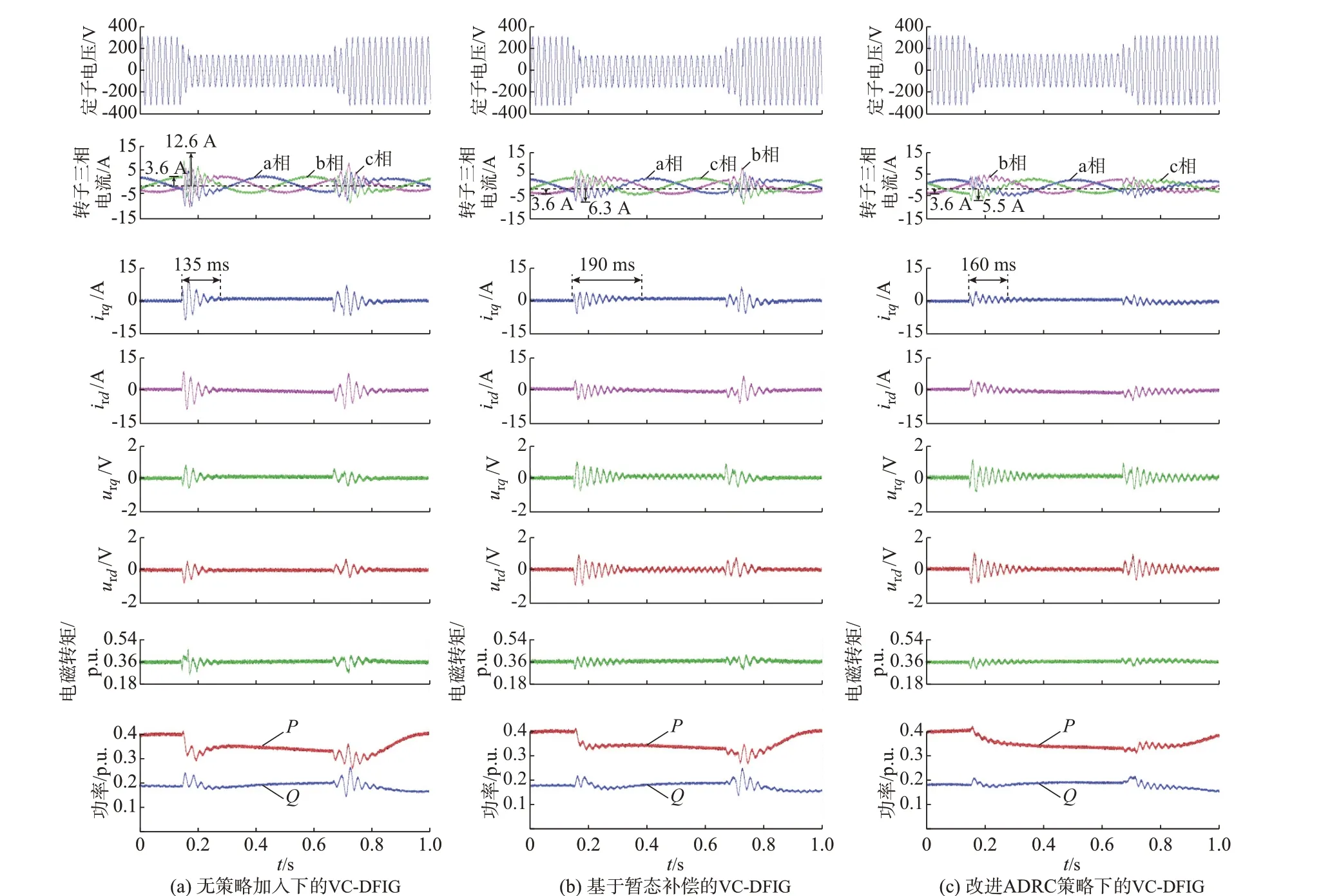
图4 超同步50%电网电压对称跌落下的实验结果Fig.4 Experimental results for super-synchronous 50% symmetric drop of grid voltage
6 结语
针对VC-DFIG 在电网对称故障下的转子过电流问题,以往的暂态补偿策略是在转子电压处补偿一定的暂态分量,但是补偿效果受电网稳定性和电机参数影响较大,鲁棒性较差。对此本文提出了一种改进ADRC 的故障穿越控制策略。一方面,所提策略对常规ADRC 在故障下的扰动估计不足进行了改进,将定子磁链获取的暂态分量作为已知扰动引入扰动补偿,进一步减小了电网对称故障下扰动补偿量与实际扰动量的偏差,提升故障下的扰动补偿速度和能力。另一方面,其通过二阶ESO 对扰动进行估计补偿,降低了故障下模型参数对实际控制效果的影响,具有较好的鲁棒性。实验结果表明,本文所提策略在电网对称故障下具有良好的转子过电流抑制能力和较好的鲁棒性。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

