核心素养视角下的2022年上海高考数学卷分析*

201101 上海市七宝中学 童永健 卜照泽

随着“双新”课改的推进，2022年是上海采用二期课改教材高考的最后一年.同时，在疫情导致上海高考推迟的影响下，对这一年的考生而言，高考注定是特殊而不平凡的.

2022年上海高考数学卷一如往常，遵循整体平稳，确保有序，又不忘突出考查学科核心素养的原则.前者体现在试题的结构体量保持稳定、全面考查基础知识、基本技能、基本思想和基本活动经验，有较多“常规”知识和技能的考查，让考生“能得分”.而后者则体现在对考生能力考查的重视，部分试题稳中有新，考查学生多元化思维、在情境中进行问题解读、在探究过程中进行思考与分析，让考生不轻易“得高分”[1].今年的高考试题对《普通高中数学课程标准(2017年版)》(以下简称“课标”)提出的六大数学核心素养均有体现.从教师的视角看，今年的高考试题对基础知识的考查比重更大，填空题、选择题整体难度偏易，解答题中档题居多，涉及的知识面广，对考生要求较高；而对考生而言，考生普遍反映今年的高考试题较往年更有难度.要顺利应对高考的挑战，围绕核心素养的复习策略和能力培养途径是值得思考的方向.

一、 注重逻辑推理素养，彰显复杂问题分析能力

课标对逻辑推理素养有如下描述：“(学生)能够在比较复杂的情境中把握事物之间的关联，把握事物的发展脉络……”[2]正如课标所指出的，今年的高考试卷在难题中特别体现对考生逻辑推理素养的考查.

对于“水平三”的逻辑推理素养，课标指出：“……对于新的数学问题，能够提出不同的假设前提，推断结论，形成数学命题.对于较复杂的数学问题，能够通过构建过渡性命题，探索论证的途径，解决问题……”[2]今年上海卷在第12、16、20、21题等位置的难题提升了不少难度，并对逻辑推理和数学抽象素养进行了较多考查，这也成为考生反映整张试卷偏难的原因之一.压轴位置问题难度的提升对考生核心素养、综合分析及数学运用能力、解题时思维的灵活运转，乃至高压下心理抗压能力都提出了更高的要求.

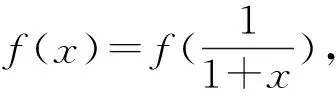
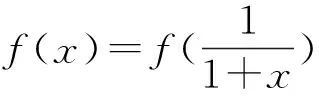
经过尝试后发现本题头绪逐步清晰，“柳暗花明”，在思考过程中，要求考生进行缜密的逻辑推理，一旦想“通”后即可快速得到答案.这类问题是典型的围绕“对于从没见过的新问题，如何去解决”的考查，对能力水平的要求较高，上海高考压轴题中也经常出现类似的问题.

例2(2022上海高考-16) 已知平面直角坐标系中的点集Q={(x,y)|(x-k)2+(y-k2)2=4|k|,k∈Z}.

①存在直线l与Q没有公共点，且Q中存在两点在l的两侧；②存在直线l经过Q中的无数个点.则( )

A.①成立,②成立 B.①成立,②不成立

C.①不成立,②成立 D.①不成立,②不成立

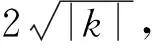
本题充分体现选择题的特点，考生通过尝试、探究及推理，可猜到正确答案，而并不用严格证明，同时，命题②的严格证明也是十分困难的.在解题过程中，脑中应有一系列以抛物线上点为圆心的圆的图像，是对抽象字母变化过程的直观想象；对于两个命题，在不同情况下分析判断获得信息，也是对直线与圆相交情况逐步明晰过程中的逻辑推理.

从近年上海高考题的命题特征看，能够通过“尝试”“猜测”解题的填空题、选择题屡见不鲜，同时这也往往是寻找思路的突破口.填空题、选择题往往有较大的思维量及较小的运算量，需要考生多分析思考，如此命题与解题的路径，也更能体现对考生综合素养的考查.

例3(2022上海高考-21) 数列{an}中，a1=1，a2=3，若对任意n(n≥2)，都存在正整数i(1≤i≤n-1)，使得an+1=2an-ai.

(1)求a4的所有可能值；

(2)命题p：若a1,a2,a3,…,a8成等差数列，则a9<30，证明命题p为真.写出命题p的逆命题q，并判断命题q的真假，若命题q为真则证明，若命题q为假，请举出反例；

(3)若对任意正整数m，a2m=3m，求数列{an}的通项公式.

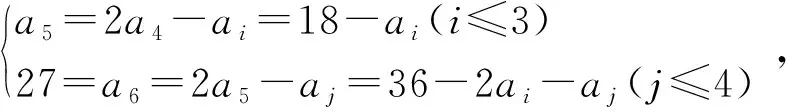
与前两年相比，今年上海高考的压轴题难度有所提升，涉及往年并不常见的数学归纳法，对部分考生而言，相对陌生的解题方法导致了难度的增加.同时，在短时间内找到问题解决的思路，并完成证明，对考生的问题分析能力、数学思想方法的灵活运用和逻辑推理、数学抽象、数学运算等素养都提出了较高的要求.

以上三题的解题思路均涉及了问题解决时的猜想和归纳，深入剖析逻辑推理素养考查的具体内涵，体现从特殊到一般的数学思想方法，也体现从具体到抽象的思维过程.分析和解决这类问题的能力是高等学府入学选拔考试进行筛选的标准，也可以作为高中数学核心素养的培育方向和目标.

二、 加强数学运算素养，助推平稳心态顺利解题

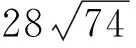
这些题目表明，在现实问题中所遇到的数据往往不是“凑”好的，而考生是否具备足够的数学运算素养，以应对复杂的现实中的运算，也是高考所希望体现的.

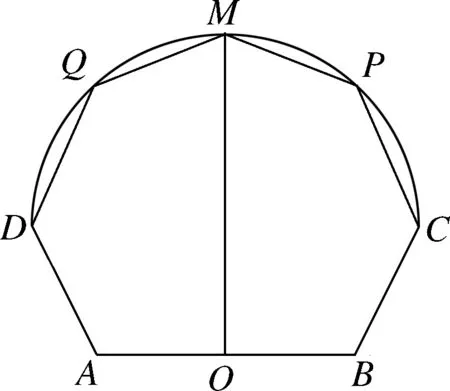
图1

例4(2022上海高考-19) 如图1，AD=BC=6,AB=20，∠ABC=∠DAB=120°，O为AB中点，曲线CMD上所有的点到O的距离相等，MO⊥AB,P为曲线CM上的一动点，点Q与点P关于OM对称.

(1)若P在点C的位置，求∠POB的大小；

(2)求五边形MQABP面积的最大值.

分析：近年来，上海高考试卷的第19题一般考查考生的数学建模素养，但今年此位置的题目仅是一道三角知识背景下的图形题，现实情境的去除应是出于平衡难度、减少阅读量的考量，在函数关系确立的过程中，仍对数学建模素养有所涉及.

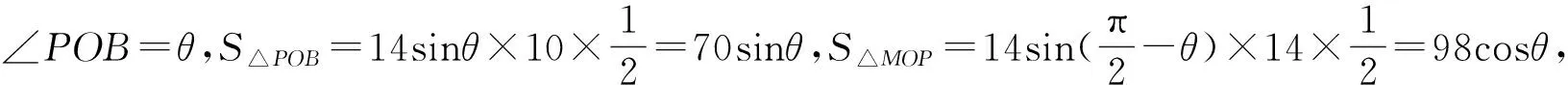
本题关系式建立相对容易，如存在现实背景，作为数学建模，应对模型和结论在现实情境下是否适用与合理展开分析.另外，本题结论数据的设置应是契合实际背景下产生的非整数或特殊值，另一方面也增加了运算量，对考生数学运算与数据分析素养的考查有所体现.

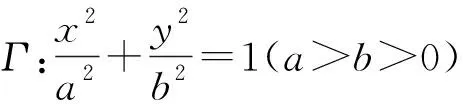
(1)若a=2，AM的中点在x轴上，求点M的坐标；

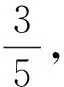
(3)若椭圆Γ上存在点P到直线l的距离为d，且满足d+|PF1|+|PF2|=6，当a变化时，求d的最小值.

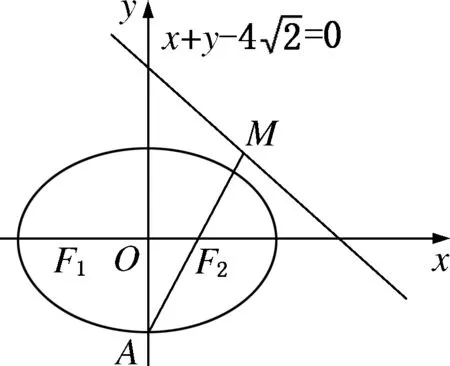
图2

分析：解析几何大题在每年高考试卷中都是对数学运算素养考查最适合的载体，2022年上海卷的解析几何问题也推陈出新，摒弃传统的设直线、联立、韦达定理，而是更多考查了数学思想方法在解题中的应用.

课标对数学运算素养要求为“理解运算对象，掌握运算法则，探究运算思路，求得运算结果”[2].可见数学运算素养并不仅指计算，也包括概念公式的理解和应用、求得结果过程中的思路、方法的探求，对问题的分析、计算路径合理性的评估等.本题将分类讨论、函数与方程的思想等融入点到直线的距离、两直线所成角等基础的解析几何公式的考查中，对考生数学运算素养同样有一定的要求.

可以看到，数学考试中的运算往往会较大程度影响考生的心态，在复习和训练中，练就较强的运算能力，以应对不同复杂程度的运算，强化考试过程中的心理承受度，能够助力考生正常发挥，顺利解题.

三、 兼顾其他核心素养，融合思想方法体现思维

在偏重逻辑推理和数学运算素养的同时，整张高考卷在其他核心素养的考查上也有所体现，融合数学思想方法的全方位考查，能较好地体现考生综合性思维，进而起到区分选拔的目的.

例6(2022上海高考-18) 已知f(x)=log3(x+a)+log3(6-x).

(1)若将函数y=f(x)的图像向下平移m(m>0)个单位，经过点(3,0)、(5,0)，求a与m的值；

(2)若a>-3且a≠0，解关于x的不等式f(x)≤f(6-x).

例7(2022上海高考-15) 如图3，正方体ABCD-A1B1C1D1中，P,Q,R,S分别为棱AB，BC，BB1，CD的中点，联结A1S，B1D，空间任意两点M,N,若线段MN上不存在点在线段A1S，B1D上，则称M,N两点可视，下列选项中与点D1可视的为( )

A.点PB.点BC.点RD.点Q

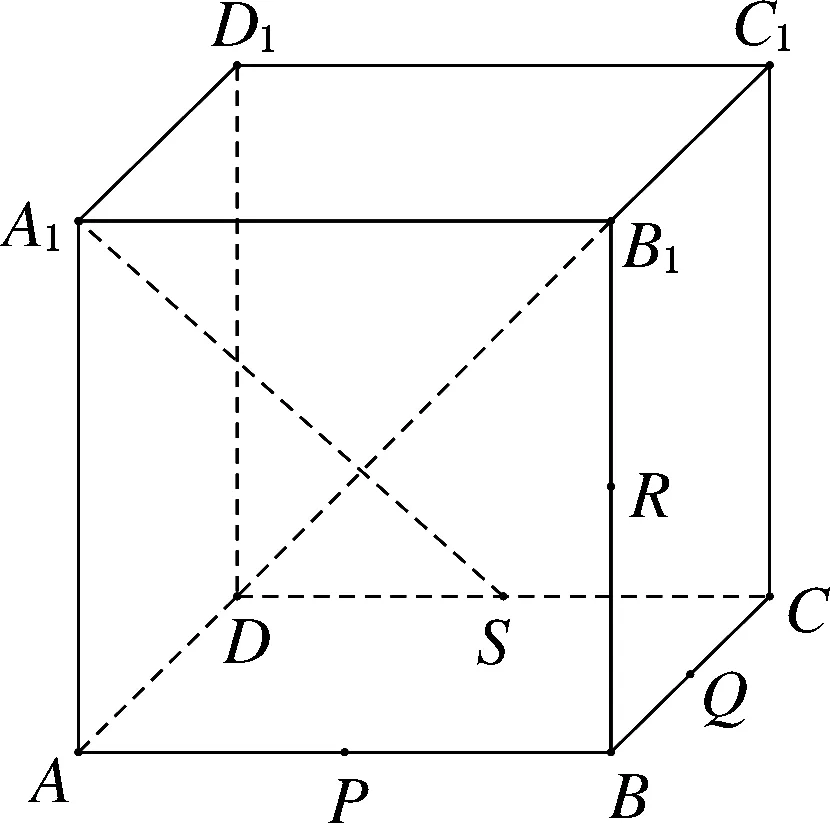
图3

分析：要顺利解决本题，应先读懂题目，题目涉及新定义的概念，能够考查学生数学抽象的素养.简单而言，本题中的“可视”即求过点D1,且与A1S,B1D都异面的直线，即求与D1A1S与B1D1D不共面的点，易知A1D1∥PS,D1D∥B1B，故选D.以立体几何为代表的直观想象素养是每年高考的必考内容，在选择题中，考生可将选项代入进行观察，前提依然是对题意的解读，在本题中化归和转化的思想体现突出.

从核心素养的视角看，无论是简单题还是难题，每道题都对一个或多个核心素养的考查有所体现，围绕核心素养引申出数学问题的解决路径和方法，不变的依然是数形结合、函数方程、化归等数学思想方法.两者并不矛盾，要顺利解决高考中的问题，特别是“新”问题，需要用思想方法“武装”思维，使核心素养有所体现，这是高考考查的目标，也是高中数学教学的重要任务.

四、 2022年上海高考数学卷带来的思考

上海高考的数学题素有“重视思维过程，简化运算过程”的特点，特别是填空题、选择题，较少有复杂的运算，却对问题的理解和分析有较高的要求.今年高考虽然在数学运算上给考生设置了一些困难，但试卷整体思维水平的体现依然远超纯运算，这也符合上海高考一直以来的趋势.高考卷的难度分配和命题方向始终有迹可循.

第一，从核心素养的视角看，高考紧密地围绕了课程标准提出的六大核心素养.每年高考卷的命题都会对各个核心素养进行全方位考查，兼顾全面性，也不乏侧重点.同时，对考生核心素养相互融合下综合能力和思维水平的考查，在中档题及难题中有较多体现.核心素养的培养过程是一个长期又复杂的工程.高考越来越多考查能力，而非解题技巧，如何让学生在学习的过程中培养自身素养，通过能力“推得”技巧，是高中数学面对的一大课题[3].

笔者认为，数学核心素养的依托是数学思想方法的渗透，用数学的思维分析问题、解决问题的训练，能够有效提升学生个人的能力水平，进而从“应试”中解放出来.高中阶段的数学教学应以知识为载体，在教学练习中不断融入和强调数学思想方法，以知识习得、兼顾能力提升为目的，双管齐下，共同关注.

第二，“双新”课改将对2023年上海高考的数学学科带来较大的变化.教师在复习和教学中依然能够遵循核心素养的培养为主线、基础知识的习得为依托、在其周围不断开枝散叶的方针，并参考多年来上海高考卷的难度、结构和命题特色，选择有针对性和适用性的复习策略.

近年来高考始终追求平稳，立足基础.题型变化不大，难度分配合理，无论是哪个层次的考生，都应放眼基础，力求“不该丢分的”一分不丢，而“努力能得分的”作为锦上添花，这是复习的方向和重点，也是确保高分的基石.要做到这一点，即要求对所学知识点有较全面的认识，学习时强化单元性，复习时站在较高的观点整体把握.数学知识切忌死记硬背，力求在理解中融会贯通.

第三，对于新教材删去的内容，在练习中应精挑细选，不加入不考的内容以增加负担.对于新教材改动的内容，教师应更多予以关注，多思考变化带来的启示，有些问题也可能来源于此，如单调和严格单调表述上的区别引发的问题，导数的工具在单调性、最值、极值求解中的引入等.

对于新增的内容，应充分研读课标，以核心素养在新内容中的融入为切入点，如概率统计(续)可能出现涉及数据分析和数学建模素养的解答题，即具有现实背景、需进行数据分析、建立一定数学模型的概率问题或统计问题.在“双新”课改中，数学建模素养特别受到关注，可以看出，2017年-2019年高考试卷的第19题对数学建模问题进行了一系列尝试和探索，在未来的高考中，侧重点可能是数学建模过程中的某个环节，也可能是对现实问题的整体解决思路，甚至可能出现开放式的主观题.在日常教学中，仍应依托新教材丰富的资源，切实组织并开展建模活动，将建模素养的培育落到实处.

第四，数学运算是数学学科较为重要的素养，学生对其的掌握往往是较为薄弱的，这同时也与考生在考场的心态与应变相关联，是一种能力的体现.计算器的使用能够在很大程度上帮助考生进行运算、观察函数的性质等，在考试中也可挖掘计算器的“巧用”，充分体现从特殊到一般的思想，特别是面对选择题，上海的高考题也较能体现填空题、选择题小题的特点.但在平时过多地依赖计算器，会使原本应得到训练的思维过程被忽视，造成反向的作用，这也应引起足够的重视.