平面带形区域上一类解析函数的Bohr现象
林珍连, 曾旭暾
(1. 华侨大学 数学科学学院, 福建 泉州 362021;2. 泉州师范学院 外国语学院, 福建 泉州 362000)
1 预备知识

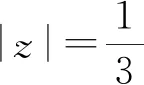

2010年,文献[5]考虑了区域Ω为一类移动圆盘,当
时,解析函数族B(Ωγ)的Bohr不等式,可得定理A.
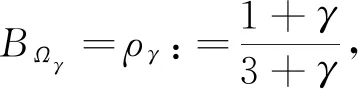
2021年,文献[6]改进和推广了文献[5]的结果,结果之一为定理B.
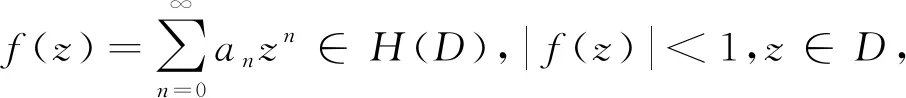
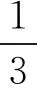
关于经典Bohr不等式的更多改进和推广,可参见文献[7-16].
文中考虑当区域Ω是带形区域S={z=x+iy∈C:-1 证明以下引理. 由于f(z)∈B(S),故|f(z)|≤1,由Schwarz-Pick引理,有 |f′(z)|≤λS(z)(1-|f(z)|2),z∈D. 特别地,当z=0时,上式化为 (1) 当n≥2时,对任何给定的正整数n,令 N为任一正整数,则有 g(z)=a0+anzn+a2nz2n+a3nz3n+…∈B(S), 再令 综上所述,引理得证. 利用引理1探讨B(S)函数族的Bohr现象,得到了这类函数的Bohr半径和两个Bohr不等式. 证明B(S)解析函数族的Bohr半径. 证明:由引理1,可得 (2) 对定理1进行一些改进和推广,首先,证明其中一个改进版(定理2). 证明:因为f(z)∈B(S),由引理1,可得 由于|a0|≤1,所以B1(r)≤1.当B1(r)=1时,有f(z)=c,|c|=1.证毕. 证明:不失一般性,记|a0|=a∈[0,1],由引理1,可得 记 g(a)=a+A(1-a2)+B(1-a)(1-a2)+C(1-a2)2,a∈[0,1]. g′(a)=1-2Aa+B(3a2-2a-1)+4C(a3-a), g″(a)=-2A+2B(3a-1)+4C(3a2-1). 因为B和C都是非负数,所以g″(a)关于a的函数在(0,1)内是单调递增函数,从而有 经计算可得a≥1,由题设可知a≤1,从而|a0|=1,由最大模原理可知,f(z)=c,|c|=1. 由引理1可知,Ω⊃D为一般的单连通区域时,有类似的结论成立.换而言之,带形区域可以推广到一般单连通区域.2 主要结果及其证明
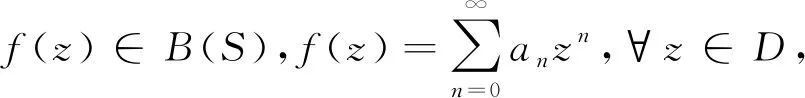


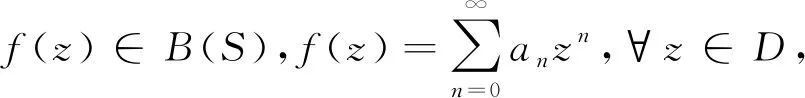
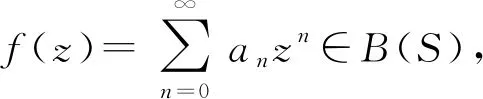

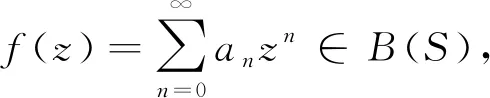



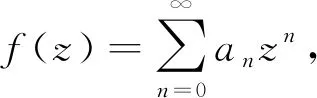
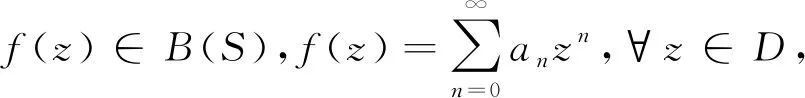


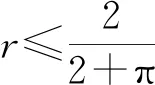


——泉州宋船

