基于机器视觉的对刀间隙检测方法研究

孙齐伟，李英

（长春理工大学 光电工程学院，长春 130022）

对刀是数控机床使用中的关键环节，加工零件的精密度由对刀精度决定。快速准确地对刀可以大大减少加工时间，从而提高产品加工的精度。对刀的生产效率很重要。机床的对刀可分为手动对刀和自动对刀［1］。手动对刀主要是人为进行，这种操作通常占用大量工作时间并且具有较大的测量误差，难以满足高精度加工的要求。自动对刀功能在一定程度上大大提高了对刀效率，它易于使用、测量准确、能实现自动和实时对刀，操作者不需要技术要求，但是，高精度对刀仪成本高、安装难度大，对刀效率的提高程度有限。

目前，计算机机器视觉技术已成为下一代智能视觉数控机床的关键部分，具有高精度、高效率、非接触、智能化等优点［2-6］。于占江等人［7］利用两个相机构建正交分布光学图像测量系统对微小车床对刀间隙检测，系统检测精度达到±15µm。宋颖慧等人［8］通过LVDT对刀装置粗定位、光学对刀装置精定位的粗精结合的方法，快速准确地测得刀具的中心高、刀尖圆弧半径以及刀具定心坐标，重复对刀精度达到1µm，实现精确对刀。HOU B等人［9］开发了数控机床计算机视觉自动对刀系统，该系统具有简单高效的对刀过程，重复对刀精度小于1µm。然而对于小尺寸工件的加工，此方法不能保证相机垂直拍摄工件xy面。

机器视觉测量容易受到环境的干扰，视场光照不均，目标表面反光等因素会影响视觉测量的准确度和精确度。本文通过顶帽变换、线性加深、图像分块、区域生长等操作一定程度上消除了光照不均和目标反光的问题，实现了目标的完整提取。本文利用基于机床坐标信息反馈的视觉系统标定方法［9］实现了相机高精度标定，并运用到机床对刀间隙检测中，精确有效地实现了机床对刀间隙的识别与检测。

1 系统总体方案设计

数控机床视觉对刀系统主要由光源、CCD图像采集模块、计算机处理系统、控制执行系统等构成。实验平台如图1所示。1号和2号CCD沿垂直刀具方向安装，两个CCD相互垂直安装。CCD模块采用IMPERX_bobcat-B2520工业相机，性能参数如表1所示。镜头采用微视的AFTZML1011工业放大镜头，性能参数如表2所示。数控机床分辨率为1µm，视觉系统精度预计为1µm。视场约为14 mm×12 mm，计算出的每个像素精度约为5.70µm。然后使用Zernike moments检测，由于Zernike moments亚像素边缘提取比传统的canny等像素级算法精度提高5～8倍［10］，理论像素精度应该达到1.140µm。

表1 相机性能参数

表2 镜头性能参数

图1 实验平台

在系统中，采用白色光源照射间隙部位，CCD相机将获取的间隙图像经由图像采集卡传送至PC机。计算机系统利用图像处理算法对获取的数字图像进行各种处理运算，提取出刀具与工件的间隙值，并以指令方式控制机床微动平台进给。

2 相机标定

在进行对刀时，要尽量使刀位点和对刀点相互重合［11］，即刀位点与对刀点的位置偏差为零。刀位点是确定刀具位置的基准点，一般选择刀具的刀尖。对刀点是指刀具相对于工件加工运动的起点。本文选择矩形工件的一角点作为对刀点，对刀过程此时指刀具的刀尖运动到工件的一个角点上。鉴于机床的高分辨率，本文采用基于机床坐标信息反馈的视觉系统标定方法对相机进行标定，该方法不需要安装特殊的校准位移测量系统。因此，标定过程简单高效，有利于可视化对刀的工程应用。

标定过程如图2所示，1号相机捕捉xz面，dx为对刀点与刀位点x方向的偏移距离，dz为刀位点到工件表面z方向的距离；2号相机捕捉yz面，dy为对刀点与刀位点y方向的偏移距离，dz同上。机床每次沿X/Y/Z方向移动100µm，记为Dm，对相应方向的距离进行图像采集和计算，求出偏移距离Dc（单位：pixel），则可计算出相机的标定系数，公式如下：

图2 相机捕捉示意图

式中，Dc（i）是第i次计算出的偏移距离。

为了提高相机标定的精确度，多次重复实验，部分数据如表3所示，则可得出相机的标定系数为：

表3 X/Y，Z轴偏移距离

3 对刀间隙检测

3.1 对刀间隙检测流程

对刀间隙检测流程如图3所示，其中图像处理阶段流程如图4所示。两个相同的相机参数相同，调整刀具与工件的偏移距离，通过相机获取的对刀间隙如图5、图6所示。

图3 对刀间隙检测流程图

图4 图像处理流程图

图5 1号相机捕捉图

图6 2号相机捕捉图

3.2 图像处理

相机采集的图像光照不均匀，刀具还存在反光现象，严重影响对刀具和工件的识别。为了完整提取刀具和工件需要进行一系列处理，处理过程如图4所示。

3.2.1 顶帽变换

图5、图6所示显示图像右上方的背景比左下方的背景亮，且刀具有反光。对不均匀亮度图像做阈值处理很困难，不能很好地将目标从背景中分离。对图像进行开运算可以产生对整个图像背景的合理估计。从原图像中减去开运算后的图像，可以生成一副具有合适且均匀的背景的目标图像，如图7所示。图中背景较均匀，目标轮廓较模糊，需要进一步分离背景与目标。经过阈值分割后如图8所示。从中可以看出，目标的轮廓大体上被提取出来了，刀具反光部分比较明显。由此，可以利用此图作为刀具反光部分的掩膜，去除刀具的反光。

图7 顶帽变换图

图8 顶帽图二值化

从原图像中减去开运算后的图像称为顶帽变换，公式如下：

式中，f为原图；∘为开运算；b为结构元素。

3.2.2 线性加深

将原图像与阈值分割顶帽变换的图像进行线性加深，如图9所示。

图9 线性加深图

线性加深的算法如下：

其中，fL为输出图像的像素值；f、g分别为两幅图像的像素值。如果两幅图像的像素值之和小于255，输出结果将会是纯黑。如果将其中一幅图像反相，结果将是纯粹的数学减。

从图9中可以看出，刀具反光部分被弥补，背景部分亮度不均匀，不能对整体图像做阈值分割。

3.2.3 区域生长

本文对图9进行上下分块，之后分别进行阈值分割，如图10（a）、图10（b）所示。

图10 分块二值图

图10（a）中刀具与背景没有完全分离，因此，本文采用区域生长方式提取刀具。区域生长是根据预先定义的生长准则，将像素或子区域组合为更大区域的过程。基本方法是从一组“种子”点开始，将与种子预先定义的性质相似的那些领域像素添加到种子上，来形成这些生长区域（如特定范围的灰度或颜色）。本文选取刀具中心线附近一点作为“种子”，进行区域生长来分割图像，生长阈值根据实验条件确定。实验结果如图11所示。

图11 刀具提取图

之后将图11和图10（b）按照图像分块之前的位置进行拼接，如图12所示。

图12 拼接图

3.3 边缘检测

为了高精度提取刀具和工件特征，本文采用Zernike moments［12］提取图像边缘。

图像的f（x，y）的n阶m次 Zernike moments定义为［13］：

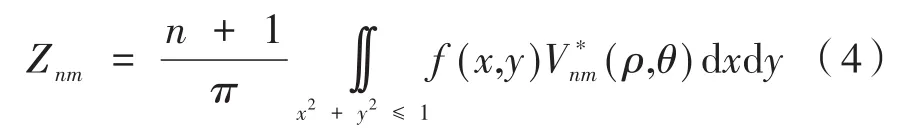
式 中，Vnm（ρ，θ）是积分函数，表示与Vnm(ρ,θ)共轭，m、n都为整数且满足：n≥0，n-|m|为偶数且n≥|m|。

假设单位圆的圆心位于图像的某个像素点上，并且图像边缘经过该圆，由此建立理想的阶跃边缘模型，如图13所示。

图13 理想阶跃边缘

图13中，k是阶跃灰度，h是背景灰度，则阴影部分的灰度值为h+k；l是圆心到边缘的垂直距离；φ是边缘垂线与x轴的夹角。将图像顺时针旋转φ角度，使边缘平行于y轴，如图14所示。旋转后的理想阶跃边缘模型的侧面剖析图呈阶梯状，如图15所示。

图14 旋转后的理想阶跃边缘

图15 理想阶跃边缘剖面

设旋转后的图像为f′（x，y），则由于旋转后的图像关于x轴对称，则：

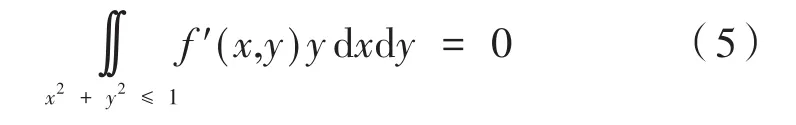
由于式（5）就是Z′11的虚部，所以存在以下关系：

由式（6）可求得图像旋转角度为：

Zernike moments的一个重要性质是旋转不变性。若一幅图像旋转φ角，则旋转前后的Zernike moments只有相角改变，幅值仍保持不变，即：

Z00、Z11和Z20对应的积分核为V00=1，V11=x+jy，V20=2x2+2y2+1，结合图16，可以推导出旋转后图像的各阶Zernike moments。

由式（9）～式（11）解得参数l、k为：

假设在边缘检测过程中采用的模板大小为N×N，结合其放大效应的修正，可以得到利用Zernike moments进行亚像素边缘检测的计算式：

其中，（xs，ys）是边缘的亚像素坐标值；（x，y）是图13中的某个像素点，也是单位圆圆心。

本文采用模板大小为7×7的Zernike moments提取目标的亚像素边缘，如图16所示。

图16 亚像素边缘提取图

3.4 对刀间隙距离计算

经过边缘检测后，刀具和工件的边缘轮廓可以清晰地提取出来，然后Hough直线变换求出工件图像上的边缘直线方程：

同时刀具的轮廓下边缘可以检测出多个像素点（x，y），根据点到直线的距离方程计算出Z方向刀尖点到对刀平面直线的距离。

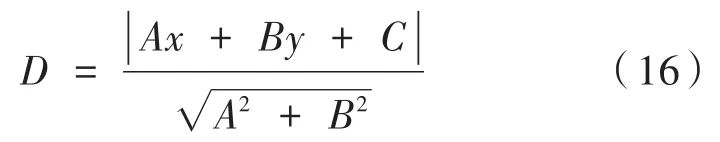
其中，D是像素点（x，y）到直线方程的距离。通过比较点到直线的距离的大小，来判断刀具的刀尖点，选择距离最小的相对应的点的像素纵坐标作为刀具刀尖的纵坐标。选择刀具两条直边的中心线的横坐标作为刀具刀尖的横坐标。利用点到直线的公式可计算出x，y方向上的对刀间隙。

4 实验结果分析

实验中，通过机床平台施加微小位移进行系统验证，在实际测试中，刀具在平台的带动下按相同位移间隔进行移动，接近待加工工件的对刀点。通过相机获得刀具图像，分别用本算法和于占江等人［7］提出的算法（简称“于算法”）测量刀具偏移距离。测量数据如图17（a）、17（c）、17（e）所示，测量误差如图 17（b）、17（d）、17（f）所示。从测量误差图中可知，本算法的测量误差比于算法的测量误差较小，说明了本算法的检测精度高。在视场约为14 mm×12 mm中，用于算法中相机标定的方法进行标定，相机的水平标定系数为5.93µm/pixel，垂直标定系数为6.84µm/pixel，相机标定精度较低。此外，于算法在像素上进行图像处理，检测精度相比亚像素检测精度较低，所以于算法的测量误差相比本算法较高。本算法的测量误差在±2µm以内，造成误差的因素有刀面线拟合时不够精确，刀具抖动。

图17 X、Y、Z方向测量数据及误差图

通过记录多次视觉系统运行时间，如图18所示。视觉系统的图像采集和处理所需的时间约为2.26 s，准确性达到了现代制造业的要求，系统速度还有待提高。

图18 视觉系统运行时间

5 结论

本文设计了一种应用于小尺寸工件加工的三维对刀间隙检测装置。通过本文图像处理部分的算法一定程度上消除了目标反光和光照不均的影响，完成了目标的完整精确提取。采用基于机床坐标信息反馈的视觉系统标定方法完成了视觉系统的标定，并实现了对刀间隙的精确测量。通过机床实验平台施加微小位移进行系统验证，实验结果表明：该检测系统能够快速有效地进行数控机床对刀间隙识别与检测，系统检测精度达±2µm，图像处理的时间消耗为2.26 s，系统的准确性达到了现代制造业的要求，系统速度还有待提高。