基于实测数据阵列式多组件虚拟装配技术研究

詹睿，朱运东，林雪竹，郭丽丽，唐钰

（长春理工大学 光电工程学院，长春 130022）

在现场装配中，受防热结构组件制造偏差、装配偏差以及工装定位偏差等因素的影响，会造成组件间间隙阶差结果超差，防热结构组件间产生的间隙阶差对装配的质量起关键作用。通过数字化三维测量技术获得防热结构组件的真实物理状态信息，取代理论数模进行装配过程仿真，并预测出因设计不当而引起的装配干涉，可以提前对组件进行修整或调姿，减少装配的次数，提高装配的效率和质量［1］。

目前对于部件间干涉的修配方法多半是人工操作，凭手工测量和视觉判断反复试装、修配或者调整姿态，导致工作量大，装配效率降低。传统的通过软件进行数字化预装配，对产品进行装配仿真检测干涉的方式也只是针对理论CAD模型，对于实际构件装配产生的干涉并未涉及［2］。

首先基于实测点云数据，进行点云分割，提取特征点，建立间隙阶差数学模型。其次以防热结构组件设计间隙阶差为约束条件，建立目标函数，优化求解调姿参数，最后经过调整寻优位姿，达到满足技术要求的最佳位姿。该方法可高效、高精度地实现组件装配调整，为后续装配提供指导意见。

1 间隙阶差数学模型建立

以线式点云数据为例，由于组件结构边界部分存在微小圆角，边界各个位置点的间隙阶差不同。根据各个边界点，分割得到相应的子点云，提取对缝边界特征点，计算各子点云间隙阶差值。

1.1 点云分割

点云区域分割时首先确定分割方向，通过构造包围盒，沿包围盒主轴方向划分区域。图1中，包围盒1234-5678可由最小坐标点1（xmin，ymin，zmin）和最大坐标点 7（xmax，ymax，zmax）确定，并与XYZ坐标系方向一致。以X轴为分割方向，可得其中一分割面 1′2′3′4′。

图1 沿包围盒主轴方向分割

将点云划分至各等分区间，如图2所示，设分割方向为X轴，则第i个分割面的x坐标xi=xmin+i× seg(i=0,1,…,U)，其中 seg=(zmax-zmin)/U为区间高度，U为区间数。

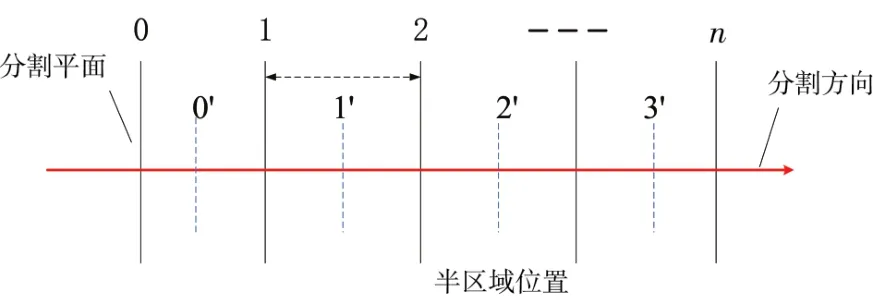
图2 等区间分割

在分割面内任取不共线的三点即可确定分割面方程，点为Pti（xi，yi，zi），i=0，1，2，分割面法矢为：

分割面方程为：

式中，常数项D=-Ax0-By0-Cz0。

区域Ui在相邻分割面Pi和Pi+1之间，则按式（2）确定数据点与区域的归属关系为：

遍历所有点云数据，若点满足式（3），则该点划归区域Ui。

1.2 切片特征点提取

点云数据用三角化网格曲面表示。在三角网格面中，通过判断邻接三角形数量来提取三角网格的边界点，对每一条边做边界边判断，邻接三角形的个数为1的边为边界边，个数为2的边为内部边［3］，从边界边中提取边界点。

将式（4）边界点投影到全局坐标系｛G｝的XOZ面，设其法向量为（a，b，c），则点(xi,yi,zi)在XOZ面ax+by+cz+d=0上投影点为(x′i,y′i,z′i)。

遍历两侧所有点云，应用估算数据点曲率算法［4］，曲率较小的点视为角点，提取出两侧边缘点上下角点。对缝侧上下角点之间的点即为边缘点，如图3所示。

图3 边缘点提取

线式点云是有序点云，设扫描线点个数为n，第i条扫描线边缘点为pi0，pij(0≤j≤n)为第i条扫描线边缘点pi0向后第j个点。如图4所示，取单条扫描线单侧的点云数据，计算点pij曲率，计算相邻两点的曲率差，并设定阈值δ，设第一个曲率差小于阈值δ的点为pi,s，角点区域为pij(0≤j≤s)，角点区域之外的点即为平面拟合点pij(s+3≤j≤s+20)。所用平面拟合算法为特征值法［5］。

图4 扫描线特征点划分

1.3 数学模型建立

根据线式点云数据的特点，构建间隙阶差数学模型，如图5所示。将平面α平移至经过左侧临界点qi1(x1,y1,z1)得到平面α′（设方程为ax+by+cz+d=0）。记第i条扫描线的实测阶差Flusui为qi2到平面α′的欧式距离，公式如下：

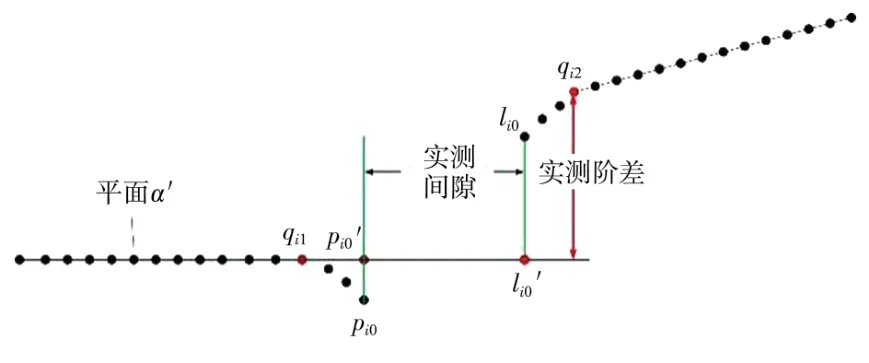
图5 基于实测数据的间隙阶差模型

扫描线右侧边缘点li0投影至平面α′，得到点li0′，左侧边缘点pi0投影至平面α′，得到点pi0′。记pi0′与li0′的点间距为该扫描线实测间隙Gapi。则该点云切片实测间隙值为：

2 基于实测数据的虚拟装配位姿参数优化建模与仿真

虚拟装配的关键是移动组件的位姿调整。移动组件为实测数据，移动组件的初始位姿为与理论数模最佳拟合匹配之后的位置。求解移动组件当前位姿参数，优化求解移动组件的位姿。各防热结构组件间隙阶差通过位姿调整优化，可得到与目标间隙阶差稍有不同的目标间隙阶差，在满足约束条件下，优化求解出移动组件的装配最佳目标位姿，进而实现组件间虚拟装配调姿仿真。

2.1 位姿参数求解

防热结构组件局部坐标系相对于空间全局坐标系的坐标转换关系可用位姿矩阵表示，如下：

式中，R∈R3×3为姿态矩阵；T∈R3×1为平移矩阵。

将移动组件局部坐标系在装配空间全局坐标系下的位置姿态参数定义为位姿参数向量：

式中，[ΔxΔyΔz]T为位置分量；Δx、Δy和 Δz分别为局部坐标系原点各分量在全局坐标系中的位置；[εx,εy,εz]为姿态分量，εx、εy和εz分别为局部坐标系各轴线相对于全局坐标系的欧拉角。位姿参数向量与位姿矩阵的关系如下：

采用三点法求解移动组件的当前位姿参数［6］。

2.2 虚拟装配目标位姿优化

在全局坐标系下的目标间隙阶差已知，但是存在装配、测量、加工、制造等误差，因此，实际的装配位姿已经无法等同于目标位姿［7］。且位姿寻优后移动组件与固定组件之间各切片点云数据已不同于调姿前用于计算的各切片点云数据，需重新对点云进行分割，计算各切片间隙阶差，再次优化位姿，在切片进行间隙阶差计算，直至实际间隙阶差与其目标间隙阶差的匹配误差最小，移动组件调姿到目标最优位姿。

2.2.1 目标函数建立

移动组件是点云数据，设移动组件共有n个点，第i（i=1，2，…，n）个点在装配全局坐标系{G}中的实际位置向量为，位姿优化后的点云数据目标位置向量为，如图6所示。

图6 装配调姿示意图

在以v=(ΔxΔyΔzεxεyεz)T为调姿参数向量对移动组件进行位姿优化后，移动组件点云数据在{G}中的位置为：

式中，k=1，2，…，l为分割点云得到切片的个数。为当前位姿固定组件的点云切片特征点与移动组件的点云切片特征点根据式（5）和式（6）在{G}中计算所得装配组件间各点云切片的间隙和阶差。

间隙阶差优化求解，采用平方加权构造目标函数，移动组件装配调整后的最佳位姿等同于目标函数最小，即：

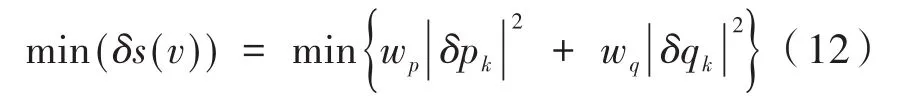
间隙阶差误差均需在允许的范围内，即：

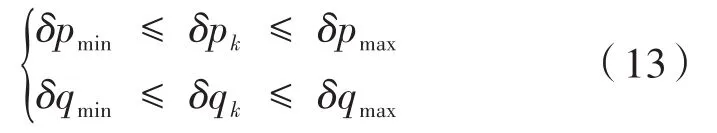
2.2.2 优化求解

采用量子粒子群优化算法［8］对装配目标位姿进行最优化求解。设置适应度函数f（v）为式（12），目标位姿中的6个参数可作为粒子的6个维度，则第i个粒子表示为一个6维的向量，i=1，2，…，N。将待求解的目标位姿作为由N个粒子组成的一个粒子群中的一个粒子i，粒子i调姿参数为：

其中粒子的更新方程为：

设置迭代次数t=1 000，设置粒子数，m=100，n为总维数，n=6；设置调姿参数的上下限为-10～10，设置初始参数为0。

Pm为全部粒子的平均最好位置；pij为第i个粒子第j维度下的个体历史最优值；Gj为粒子群体的全体最优值；φ和uij（t）服从（0，1）的均匀分布；α为收缩扩张系数，一般随迭代而更新，初始一般取为0.8，更新公式为：

式中，α1、α2分别为α的初始值和最终值；Tmax为预设的最大迭代次数。

QPSO算法步骤简述如下：

（1）初始化粒子群中各粒子的位置Xi（0），如公式（19）所示，6个调姿参数为移动部件当前位姿，初始位姿个体最优位置Pi（0）=Xi（0）；

（2）由式（15）计算本次迭代中所有粒子的平均最优位置Pm；

（3）对比粒子i第t次和第t-1次迭代适应值，如果f［Xi（t）］＞f［Pi（t-1）］，则Pi（t）=Pi（t-1），否则Pi（t）=Xi（t）；

（4）计算该次迭代的全局最优位置，即G（t）；

（5）对比个体和群体的最优值更新全局最优值，如果f［Pi（t）］＞f［Gi（t-1）］，则G（t）=G（t-1），否则G（t）=Pi（t）；

（6）根据式（18）计算粒子的新位置；

（7）重复步骤（2）至步骤（6），直至满足循环结束条件。

得到满足条件的最小适应度值fmin(v)，可得调姿参数向量v。

由于优化后计算间隙阶差特征点发生变化，优化得到的间隙阶差与当前位姿下实际间隙阶差有偏差，需重新进行点云分割计算间隙阶差，调整移动组件，直至最优目标位姿。调整流程图如图7所示。

图7 调整步骤

2.3 仿真

以两块实测防热结构组件为例，将两块防热结构组件最佳拟合匹配至理论数模下，如图8所示。

图8 全局坐标系下的实验组件点云数据

左边为固定组件，右边为移动组件。最佳拟合匹配过后的移动组件在全局坐标系下的位姿为初始位姿。对组件点云分割4次得到5块切片，去掉中间两个切片，如图9所示。

图9 组件点云切片

提取切片点云特征点，计算3块点云间隙阶差以及调姿参数，如表1所示。

表1 初始位姿3块点云切片间隙阶差值

第一次调姿优化后的间隙阶差以及适应度函数值如表2所示。

表2 第1次调姿优化后当前位姿3块点云切片间隙阶差值以及适应度函数值

第1次优化间隙阶差值与目标值比较如图10所示。

图10 第1次优化间隙阶差值与目标值比较

第二次调姿优化后的间隙阶差以及适应度函数值如表3所示，目标间隙阶差值相比第一次优化后的位姿更接近目标间隙阶差如表3所示。

表3 第2次调姿优化后当前位姿3块点云切片间隙阶差值以及适应度函数值

第2次优化间隙阶差值与目标值比较如图11所示。

图11 第2次优化间隙阶差值与目标值比较

如图12所示，经过6次适应度值优化后得到的适应度值不再减小，反而增大，得到的实际间隙阶差与目标间隙阶差误差最小。

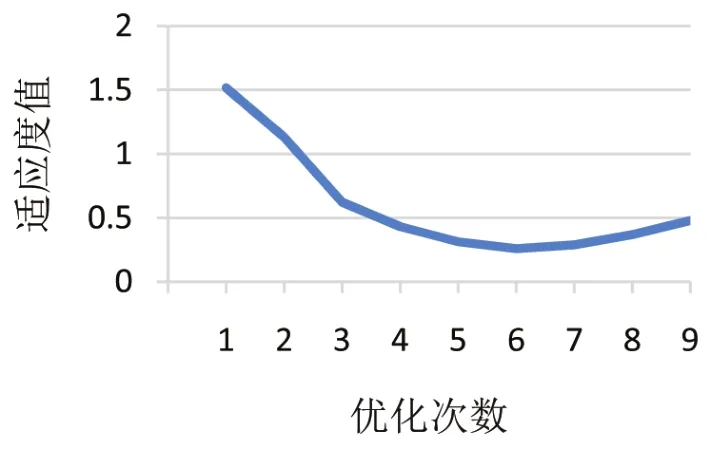
图12 适应度值与优化次数变化关系

第6次优化间隙阶差值与目标值比较如图13所示。

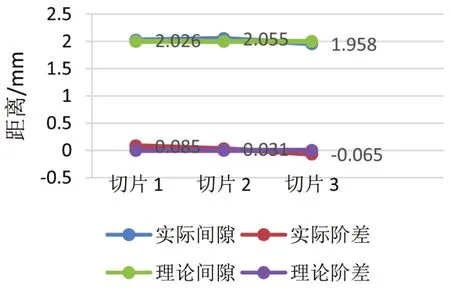
图13 第6次优化间隙阶差值与目标值比较

如表4所示，即当前位姿为装配质量最好的位姿，移动组件当前位姿可用三点法求解［6］。

表4 第6次调姿优化后当前位姿3块点云切片间隙阶差值以及适应度函数值

3 实验

如图14所示，试验件为14个防热结构组件，对基于实测数据的阵列式组件虚拟装配进行验证。

图14 试验件

用HandyScan三维扫描仪获取试验件点云数据并进行数据处理，与理论数模最佳拟合匹配，其中，设定理论数模间隙为2 mm，阶差为0 mm，得到在全局坐标系下的点云数据，如图15所示。

图15 与理论数模最佳拟合匹配后的实测数据

如图16所示，以组件7和8为例，存在组件间间隙不均匀的现象。

图16 组件7和8截面

对组件7与8进行点云分割，等间距分割3块切片，取样外侧2块点云切片，如图17所示

图17 组件7与8外侧点云切片示意图

提取特征点，建立间隙阶差模型，计算得点云切片间隙阶差，如表5所示。

表5 装配前组件10和11点云切片间隙阶差值

操作步骤同组件7和8，对所有组件间进行切片提取间隙阶差，如图18所示。

图18 各组件对缝点云截面位置示意图

经过计算得各位置点云切片间隙阶差值，如表6所示。

表6 装配前组件对缝处点云切片间隙阶差

如图14所示，组件1和4有限位孔，为定位固定组件，组件1和4根据圆孔约束定位调整后不动，完成调整的组件位置锁定，不再变动，移动组件以固定组件为基准调姿。其他组件以固定组件1和4为基准，调整顺序为2-3-5-6-7-8-9-10-11-12-13-14，装配步骤流程如图7所示。设计目标间隙为2 mm，阶差为0 mm。

经过虚拟装配后，所有组件在全局坐标系下如图19所示。

图19 装配后的组件点云数据

组件7和8对缝间截面如图20所示。

图20 组件7和8截面示意图

如表7中数据所示，经过装配后，防热结构组件7和8对缝间间隙和阶差与目标值偏差均小于0.1 mm，防热结构组件经过点云分割计算（步骤同上），所有组件间切片间隙阶差如表7所示。

表7 装配后组件间对缝处点云切片间隙阶差

装配前各防热结构组件，切片间最大间隙阶差散点图如图21所示，最大间隙偏差在0.1 mm以下的占14%，最大阶差偏差在0.1 mm以下的占21%。

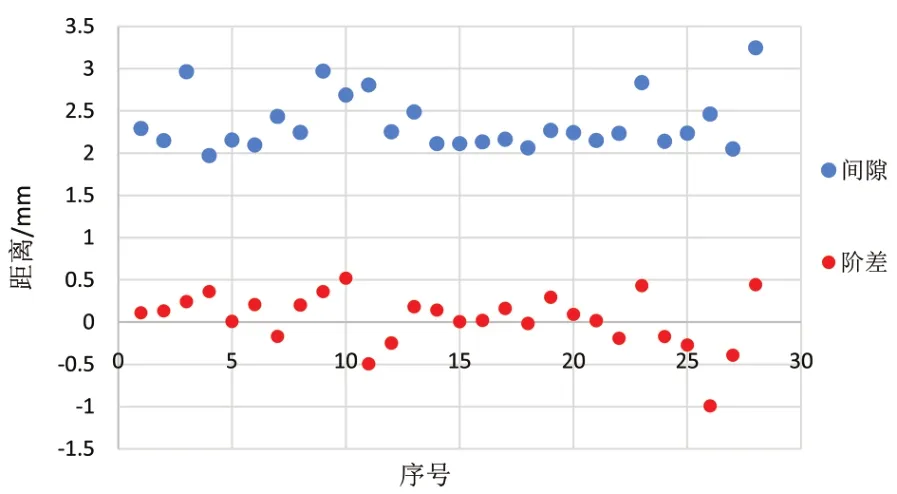
图21 装配前各防热结构组件最大间隙阶差值

装配后对各防热结构组件切片间最大间隙阶差进行统计，如图22所示，装配后各防热结构组件，最大间隙偏差在0.1 mm以下的占93%，阶差偏差在0.1 mm以下的占100%。（目标间隙为2 mm，目标阶差为0 mm）。

图22 装配后各防热结构组件最大间隙阶差值

各防热结构组件经过装配后趋近于目标值，实现了高精度装配位姿调整。

4 结论

对基于实测数据阵列式组件虚拟装配技术进行了研究，建立基于实测数据的间隙阶差数学模型，分析了实测数据的特点，在此基础上，建立基于实测数据的虚拟装配位姿优化模型，最终调姿寻优到最佳目标位姿，完成基于实测数据阵列式组件虚拟装配。

基于实测数据阵列式组件虚拟装配方案可高效、高精度地实现组件装配调整，为实际现场装配提供技术保障。