基于Matlab的结构光系统标定及三维重建

唐娟娟， 张正平， 周 骅， 赵 麒

（贵州大学大数据与信息工程学院，贵阳 550000）

0 引 言

基于结构光的三维重建技术凭借其高准确度、低成本、高稳定性、易操作等特性成为目前应用最广的三维重建技术［1］。编码结构光方法常用的有单目结构光和双目结构光［2］两种方法，二者均基于三角测量原理，它们在系统的标定上有所不用，双目结构光［3］需要先对两个相机单独标定再进行联合标定，不需要对投影仪进行标定，在提取相位信息后需要进行相位匹配［4-5］。单目系统是通过单相机和投影仪建立三角关系［6］，不仅需要对相机进行标定且需要对投影仪进行标定，投影仪无法像相机那样获取图像信息，这也是投影仪标定的难点所在，由于单目系统标定中无需进行双目的相位匹配，在获取相位信息后可通过标定获得的系统参数直接转换得到三维坐标信息，更能满足高速率的需求。

单目结构光中相机标定已经趋于成熟，以张正友相机标定法为代表。在Matlab中已有对应的工具箱，使相机的标定实现简单易操作且具有较高的准确度和稳定性［7］。为解决投影仪的标定［8］，目前已有以下方法：

（1）基于平面的投影图案法。该方法本质上是基于二维投影点和其三维的对应关系，通过将投影仪视为2D图像强度映射为3D射线的反向相机，使投影仪的校准与相机的校准相同，该投影仪标定方法的准确度依赖于事先标定好的相机准确度。文献［9-11］中本质上与投影棋盘格图案原理相同，均是基于二维投影变换理论，建立二维相机图像像素坐标和三维投影仪坐标的对应关系。这种方法在实现上较为简单，但是标定的准确度较低，以至于影响最终三维重建的准确度。

（2）经典相位法。通过求解相位信息，基于相位和高度的关系求解三维高度信息，这种方法需要辅助硬件设备让相机投影仪处于一种严格的位置关系：摄像机光心与投影中心位于同一直线且平行于参考平面，摄像机光轴要与投影仪的光轴相交于一点，此点要位于参考面上，摄像机Y轴要与投影的光栅条纹保持平行［12］。此种方法虽无需进行标定，在具体应用中难以实现，摄像机和投影仪的光心以及光轴为虚拟的，难以确定，此外，在实现三维测量时难以将工作面调整至参考平面，这些都要求复杂且昂贵的精密设备支持。

（3）新型标定法。为解决传统光栅投影模型的严格位置约束条件，众多研究学者对此进行了一系列的改进研究。已有一些方法放宽了相机、投影仪光心连线平行于参考平面的要求，此类方法仍然存在位置约束，如相机光轴与投影仪Y轴的平行要求以及二者光心需相交于参考平面一点。

本文研究了基于编码结构光中的相位测量轮廓术（Phase-Measuring Profilometry，PMP）的三维重建。采用整体建模的一种方法，此方法完全没有系统的位置约束，通过多项式将投影仪参数拟合到8个未知参数中，无须再进行复杂费时的投影仪标定，能够保持很好的稳定性及准确度。这种方法在文献［13］中由盖绍彦、达飞鹏首先提出，文献中已对其原理进行了详细的推理说明，难点在于其复杂的数学计算，以及多项式的拟合，本文将这种标定技术完全移植到Matlab平台，运用其高效的数值计算［14］和矩阵运算功能，实现高效简单明了的系统标定。通过得到的标定参数，在Matlab实现物体的三维重建，结果表明，三维重建效果好，并有较高的准确度。

1 系统标定

1.1 相机标定

相机获取物体图像，实质为物体三维坐标到像素坐标的转换，经历了4步坐标系的转换，转换过程如图1所示。三维重建的实质是通过相机和投影仪实现图像二维坐标到物体三维实际坐标，也就是相机成像的逆过程。从世界坐标到相机坐标的变换为刚性变换，其中包含物体相对相机坐标系的位置关系，也就是对相机标定所要求的外部参数R矩阵和T矩阵，R为物体和相机的旋转关系，T则包含了平移关系。相机内部参数则与相机和物体的相对位置无关，只和相机本身制作有关，一般将相机内部参数整合起来称为一内参矩阵

式中：fx、fy分别为在图像像素坐标在u轴和v轴方向的焦距；u0和v0为原点在图像像素坐标下的坐标。相机由于其镜头等构成，无可避免的存在着一些畸变，一般分为径向畸变和切向畸变，本实验采用的工具箱忽略切向畸变，默认为0。

综上，相机标定即对其内外参数的求解。根据张正友相机标定法，打印制作棋盘格标定板，对棋盘格标定板进行平移、旋转等变换并进行拍摄。使用Matlab配置的工具箱（Camera Calibrator），在APP内找到Camera Calibrator并打开，添加采集到的不同位姿下的棋盘格图片，输入棋盘格实际尺寸。本次实验制作的棋盘格标定板的棋盘格尺寸为1 cm，图片全部导入之后，点击Calibrate，即可得到相机内参矩阵

标定板和相机的相对位姿关系，如图2所示。

根据位姿图片的重投影误差，选择误差较大的图片点击删除，经过筛选之后，本次标定图片为30张，重投影误差的总平均误差为0.33像素，如图3所示，标定完成后选择Export Camera Parameters导出标定结果，存储为camera Params.mat文件，可用于后续调用。

1.2 基于多项式拟合的结构光系统标定

根据达飞鹏等［1］的新型相位法系统模型，主要包含了相机坐标系、被测物的相位信息以及世界坐标系的关系。这种新型模型对相机、投影仪、被测物体不再有严格的位置约束。论文中对物体的像素坐标以及相位信息，例如点P（m，n，θ）同其在相机坐标系中的三维坐标（Xc，Yc，Zc）的转换关系做了详细推导，再用相机坐标系中的该点三维坐标（Xc，Yc，Zc）求出该点的世界坐标：

㉓松村俊夫:《南京大屠杀大疑问》，赵博源等译，新华出版社2001年版，第111～116、130～132、135～139页。

式中，ρ为比例因子ρ＝Zc。而内参矩阵A、旋转矩阵R、平移矩阵T已经由Matlab工具箱得到，基于多项式拟合的结构光系统标定其实就是对关系式中的8个参数a1～a8的求解。将式（1）变形如下：

由式（4）可知，将系统标定转化为求解方程的问题，该方程中由8个未知参数，需要8个及以上的线性独立方程，即需要多个样本点（Xc，Yc，Zc，θ），代入方程中，通过求解方程组来求得a1～a88个参数。在采集样本点时需要注意，样本点不可全部位于同一平面，因为方程组需要保持互相独立，才有解，至少需要采集两个位姿及以上的样本点。其中样本点的相位信息θ通过5步相移法获得，像素坐标（m，n）可通过调用Matlab函数detect Checker board Points来获得采集棋盘格图片角点的像素坐标。标定时标定板上的棋盘格坐标的二维坐标易得，设标定板上点Q坐标为（a，b），建立Z轴垂直于标定板平面的世界坐标系Ω0，因此该坐标系下点Q坐标为（a，b，0），根据式（3），点Q在相机坐标系如下式所示：

结合旋转矩阵特征，由式（2）和式（5）推导得相点坐标即像素坐标求解该点相机坐标系坐标：

由式（6）可知，通过此对应关系求解标定板上点对应相机坐标系下的坐标（Xc，Yc，Zc）。将多个样本点代入式（4），可得

多项式拟合的结构光系统标定具体步骤如下：

步骤1选取相机标定用到的30个位姿中的10个位姿，通过Matlab批量处理图片，提取角点坐标并保存，选取每张图片中的4个角点，根据式（5）调用相机标定结果参数，得到40个样本点在相机坐标系下的坐标（Xc，Yc，Zc），并进行存储（见表1）。

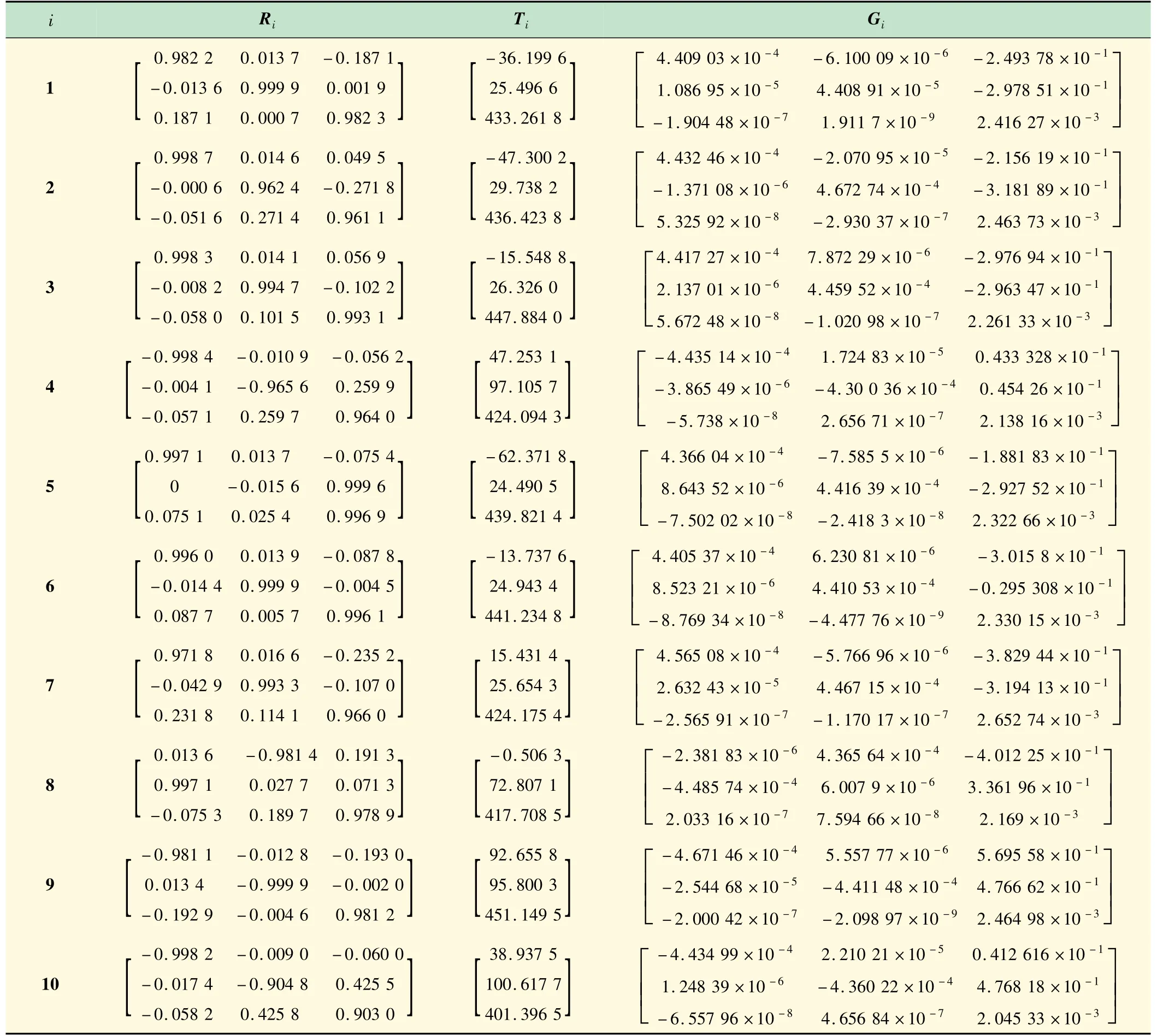
表1 标定时所用的R、T、G

步骤2硬件设备由微视传感MEMS编码结构光的投射模组、500万像素的USB工业相机（搭载850 nm窄7带滤光片）、计算机组成，如图4所示。将正弦条纹图样投影在棋盘格标定板上，采用5步相移的方法，使用Matlab控制模组投影以及相机抓取图片，完成图片采集和处理，对灰度光栅调制图进行高斯降噪，再对展开相位图进行中值滤波，使得被测物特征点提取更准确，相位展开更平整，噪点更低。获得每一位姿图片采样点的相位信息并进行存储。

算法流程如图5所示。

2 三维重建

采用编码结构光方法，通过控制投影模组向物体表明投射正弦条纹，投射的条纹由于受到物体表面的调制，存储物体的三维结构信息。投影后，使用相机捕捉调制后的条纹图案，对采集的图片进行提取灰度图、高斯降噪、中值滤波等处理，根据三角测量法即可得到被测物体的三维坐标信息。

得到a1～a88个参数后，摄像机拍摄被测物体，得到其像素坐标，通过投影仪采用5步相移法求取被测物体上各点的相位信息并进行保存。由式（1）、（2）可知，由所得参数a1～a8以及相位信息求得各点在相机坐标系下坐标（Xc，Yc，Zc），在求各点相机坐标系时，将式（1）、（2）变换成矩阵形式：

由式（3）可知，结合该位姿下的旋转矩阵和平移矩阵得到各点的世界坐标（X，Y，Z）。实验结果分别用经典法相位模型和新型相位法模型在Matlab上实现不同物体的三维点云可视化。图6为经典法相位模型下重建出的羽毛球，可见，整体重建结果与实际物体相比失真较大。图7为采用新型相位法模型重建出的羽毛球，经对比可知，该方法下的羽毛球重建效果较好。表2中为对不同物体在2种方法下的测量结果及相对误差对比，可见，基于该模型的8参数标定法能够减小误差，得到比较好的三维重建效果。

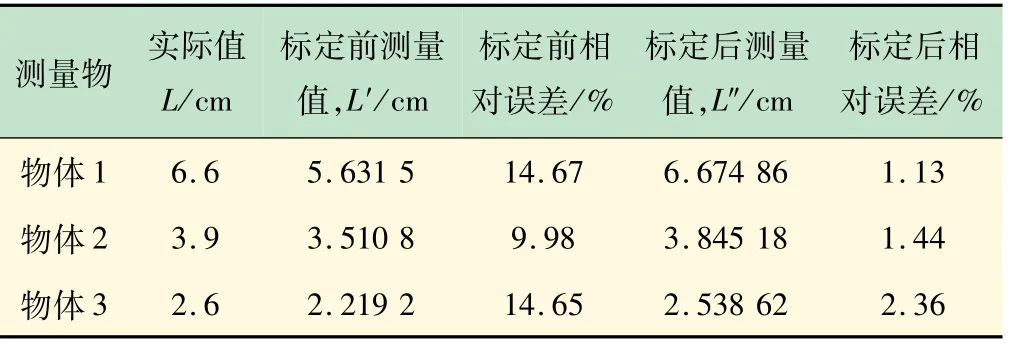
表2 三维测量实际值与测量值

3 结 语

经过对多种物体进行重建，结果表明，新型相位法重建准确度高、速率快。利用Matlab的高效数学计算功能和其便捷的工具箱，只需进行一次系统标定，即可对不同物体进行三维重建，简化了系统标定，对物体的相对位置不再有严格要求，提高了三维重建的速率和准确度。后续可从以下方面进一步提高三维重建的准确度：

（1）实验过程中，棋盘格标定板为打印制作，应注意为一个平面。标定板的准确度直接影响最后结果准确度，可购买精密制作的标定板，目前市场上已有多种标定板可以供选择，且价格适宜，提高标定板准确度可作为一种较为简单的提高结果准确度的方法。

（2）相机采集到的图片有一定的失真，可采取图像处理的方法，利用标定得到的参数对其进行图像去畸变，以提高结果准确度。

（3）实验中发现，使用Matlab自动控制5步相移图片的采集与手动控制图片采集相比，虽然提高了采集速率且操作简单，但是容易出现误差影响结果准确度，可通过控制Matlab采集间隔来减小误差。