140 t铁水罐车动力学性能分析*
景安洲,阳光武,肖守讷,杨冰,朱涛
(西南交通大学牵引动力国家重点实验室,成都 610031)
铁路运输中主要采用罐车装运各种液体和粉末状货物,如原油、液氨、酒精和铝粉等。冶金部门经常需要对铁水这类高温液体进行不同场地之间的转运,铁水罐车以其装卸简便、载运量大以及效益高的优势应用而生。特种铁水罐车一般轴数较多、结构复杂,而且受厂房占地面积的限制,从炼铁厂到转炉厂的线路主要以小半径曲线为主,而该类车辆具有的特点使得曲线通过比较困难,如设计不当,将造成脱轨、倾覆等安全事故[1]。因此根据车辆动力学参数、运行线路条件和运行工况,对140 t铁水罐车的空、重车进行小曲线通过安全性计算分析。
张良威[2]通过设置6种曲线工况对比分析了某铁水罐车的曲线通过安全性,各项安全性指标均符合GB 5599—85的规定,且R150 m工况的曲线通过性能比其他工况差。秦靖[3]总结了铁水车的整体结构设计方法,应用有限元仿真对车架进行了强度校核,通过模态分析和谐响应分析得到了外在简谐载荷对车架动态性能的影响规律。王竣[4]以鱼雷铁水罐车为研究对象计算了其稳态通过平面曲线的几何关系和低速通过S型曲线的安全性指标。叶红奕[5]简述了220 t铁水罐过跨车的设计要求及结构特点,通过计算优化参数对构件进行了详细的强度校核,为同类型的特种车辆设计提供了参考。为确保文中的研究对象140 t铁水罐车通过小半径曲线时的安全性能,建立了详细的动力学模型,对铁水罐车的空、重车分别进行了动力学性能计算分析。计算结果评定严格按照GB/T 17426—1998《铁道特种车辆和轨行机械动力学性能评定及试验方法》进行。
1 140 t铁水罐车动力学模型
1.1 车辆结构
140 t铁水罐车主要由1个车体(包括铁水罐、U型车架等)、2个焊接构架、6个轮对等组成。铁水罐有效容量≥140 t,净容积为22.3 m3,主要由罐体、吊轴、罐底、翻包机构和流嘴等组成。车体与焊接转向架采用心盘和旁承承载,上下心盘可以相对摩擦转动,且两者之间设有间隙旁承,可提供抗侧滚刚度。轴箱与构架之间设置了三卷钢圆弹簧组成的弹簧组,不同的自由高可满足空、重车所要求的静挠度及刚度,以提高动力学性能。此外,三轴转向架中间轮对各旋修削薄10 mm,以增大轮缘与钢轨的横向间隙,提高曲线通过的安全性。
1.2 动力学模型
基于该铁水罐车的结构组成和参数,分析其拓扑关系如图1所示。采用多体系统动力学方法建立了140 t铁水罐车的动力学模型,各刚体部件通过铰、约束和力元与系统或相互之间进行连接,并充分考虑了轮轨接触的非线性特性。为避免曲线轨道阻力导致通曲速度降低以致不能通过S型曲线,采用9号铰接连接车体与大地;一系弹簧组采用非线性刚度曲线准确模拟空、重车时的实际服役性能。心盘作为铁水罐车的重要承力部件,将其视为理想均匀面接触状态,整个接触面的摩擦力矩为式(1)、式(2)[6]:

图1 车辆结构拓扑关系

式中:f为摩擦系数;N为上下心盘处的垂向力;R1和R2为心盘的内径和外径;F为接触面上的总摩擦力;re为等效摩擦半径。
此车辆模型采用子结构方法进行建模,其中轮对、转向架均视为子结构。转向架模型如图2所示,整车动力学模型如图3所示。车辆系统坐标根据铁道坐标系规定为车辆运行方向为x轴,轨道横向为y轴,垂直于轨道向下为z轴。
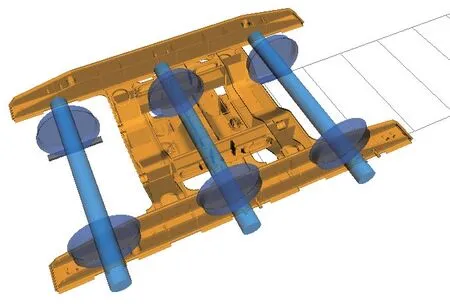
图2 转向架动力学模型

图3 整车动力学模型
2 动力学性能指标
140 t铁水罐车属于特种车辆,因此其动力学性能严格按照GB/T 17426—1998《铁道特种车辆和轨行机械动力学性能评定及试验方法》评定[7]。
脱轨系数应符合式(3)、式(4):
第一限度:

第二限度:

式中:Q为爬轨侧车轮作用于钢轨的横向力;P为车轮作用于钢轨的垂向力。第一限度为容许值,第二限度为安全值,下同。
轮重减载率应符合式(5)、式(6):
模糊PID控制器采用单片机编程设计,由于MSP430单片机内部没有专用的浮点数处理器,因此在数据的处理过程中,浮点数的计算是通过特定的算法程序来实现,如果采用浮点数计算来进行数据处理,将消耗大量的CPU资源,同时数据的处理周期较长,影响其单片机的实时控制,因此在数据处理时应尽量少用实型数据计算处理。在实际设计中将浮点数的小数部分放大,在满足精度要求的基础上,尽可能采用整形数据来处理数据计算,也可以采用长整形来实现数据的处理(见图4)。
第一限度:

第二限度:

式中:ΔP为轮重减载量;Pˉ为左右侧车轮的平均轮重。
轮轴横向力应符合式(7):

式中:H为轮轴横向力;Pst1、Pst2为左、右车轮静载荷。由名义力计算空车静轮重为73.27 kN,则轮轴横向力的限度值为75.03 kN。重车静轮重为182.98 kN,故轮轴横向力的限度值为168.28 kN。
车辆倾覆系数应符合式(8):

式中:Pd为车辆同一侧车轮的动载荷;Pst为相应车轮的静载荷。
3 动力学性能计算
3.1 线路型式
受厂房占地的限制,140 t铁水罐车的实际线路为S型小半径曲线,主要由直线段、缓和曲线段和圆曲线段组成,其中圆曲线半径为R100 m,夹直线长度为19 m,运行线路条件相对恶劣。实际运行中空车的最大通曲速度为15 km/h,重车最大通曲速度为10 km/h。依据实际运行线路条件和TB 10098—2017《铁路线路设计规范》,轨道采用S型曲线模拟,根据表1可知曲线轨距加宽值取15 mm。得到此车辆的线路构造为:30 m直线+10 m缓和曲线+50 m圆曲线+10 m缓和曲线+19 m直 线+10 m缓 和 曲 线+50 m圆 曲线+10 m缓和曲线+30 m直线。
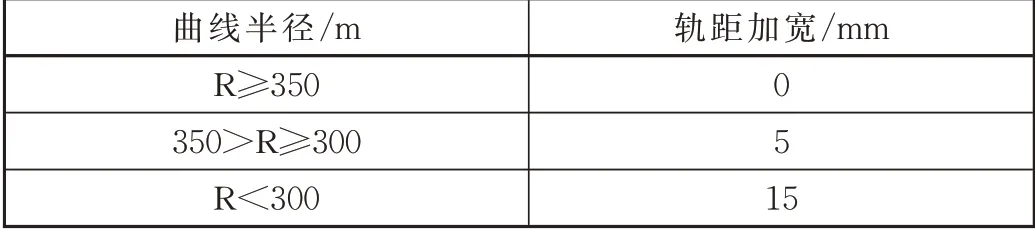
表1 曲线轨距加宽标准[8]
轨道激励谱是指实际线路的几何状态受各种因素的影响而表现出明显的随机性,如轨枕间距不均匀、路基下沉等。文中采用与轨道实际状态相近的美国五级轨道谱[9]进行计算,因此在将来的线路维护中也必须达到5级线路的要求,即《铁路线路修理规则》中的保养标准。
垂向不平顺谱密度为式(9):

横向不平顺谱密度为式(10):

水平不平顺和轨距不平顺具有相同的谱密度,为式(11):

式中:Ω为空间频率;K为系数;Av、Aa为表征不平顺程度的参数;Ωc、Ωs分为通带截断频率、止带截断频率。
3.2 临界速度分析
非线性临界速度的计算是在时域中让带有阻力的车辆以一定初速度通过一段有激励的线路,再在光滑线路上运行,当轮对的横移量小于0.1 mm时认为收敛,对应的速度即为非线性临界速度。140 t铁水罐车的非线性临界速度如图4、图5所示。

图4 空车第一位轮对横移量

图5 重车第一位轮对横移量
可以看出该铁水罐车空车状态下的临界速度为62 km/h,重车状态下为69 km/h,均大于最高运行速度,能够满足运行要求且稳定性裕量较大。
3.3 几何曲线通过性能
几何曲线通过主要研究车辆与线路的几何关系和车辆自身有关部分在曲线上的相互几何关系,用于确定车辆所能通过曲线最小半径和为此目的所需要的轮对横动量;给出转向架通过曲线时的转心位置;确定在曲线上转向架对于车体的偏转角等[10]。基于几何关系的分析,提高车辆通曲性能采取的措施一般有轨距加宽和增大轮对横动量。三轴转向架曲线通过能力相对较差,文中依据几何曲线通过的相关理论解法编制程序进行求解,考察铁水罐车的几何曲线通过能力。
为保证车辆在线路上顺利运行,钢轨与轮缘外侧之间应具有一定的间隙,为式(12):

根据现行《铁路技术管理规程》:直线轨距A=1 435 mm,轮缘内侧距B=(1 353±3)mm,离轮缘顶点18 mm处的轮缘厚度t=33+0-10mm,σ为直线钢轨内侧与轮缘外侧的全间隙。根据式(12)求得σ=16 mm,此外曲线加宽15 mm,转向架中间轮对左右轮各削薄10 mm,一系位置横向总间隙为12 mm,计算得到中间轮对轮缘与钢轨的总间隙为51 mm,轮对横动量为12 mm,车辆的横向总间隙为63 mm。
计算中所需要的车辆结构和线路参数见表2,计算结果见表3。
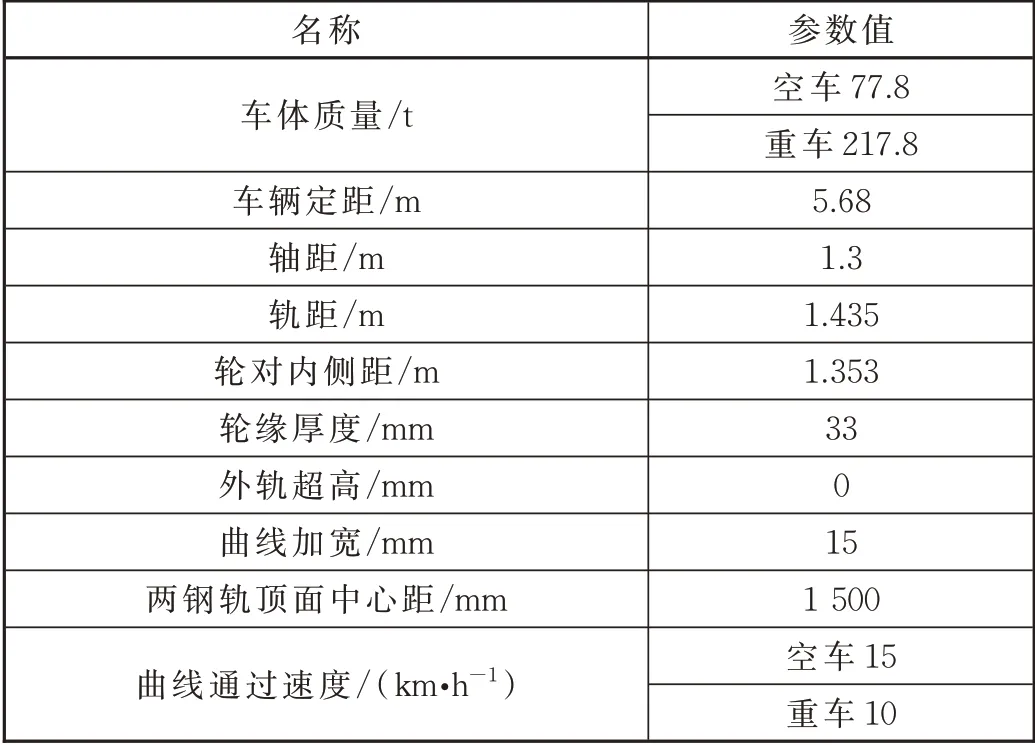
表2 车辆结构和线路参数
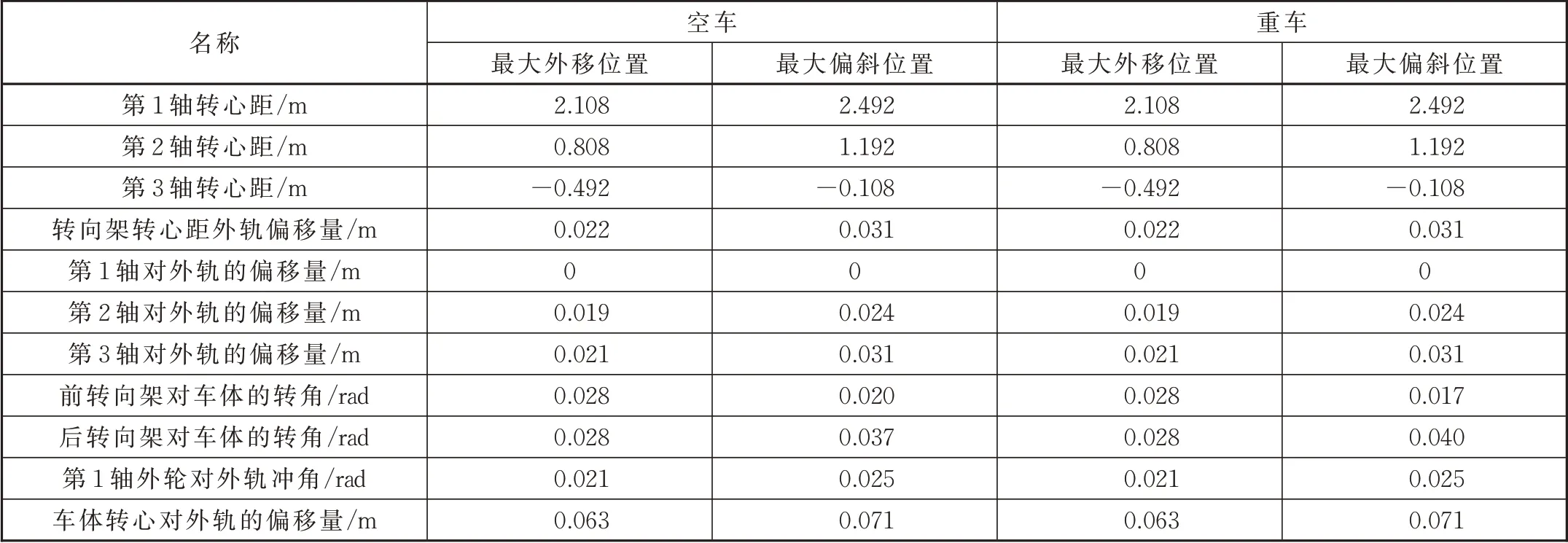
表3 几何曲线通过性能计算结果
假设前、后转向架处于最大偏斜位置,计算得到空、重车第二轴对外轨的偏移量均为0.019 m,小于轮缘与钢轨的总间隙0.051 m,即第二轴不贴靠外轨也不贴靠内轨;第三轴对外轨的偏移量均为0.031 m,等于轮缘与钢轨的总间隙0.031 m,即第三轴刚好贴靠内轨,满足R100 m几何曲线通过性能。
假设前、后转向架处于最大外移位置,计算得到空、重车第二轴对外轨的偏移量相等,均为0.024 m,小于轮缘与钢轨的总间隙0.051 m,即第二轴不贴靠外轨也不贴靠内轨,第三轴对外轨的偏移量均为0.021 m,小于轮缘与钢轨的总间隙0.031 m,即第三轴既不贴靠内轨也不贴靠外轨,满足R100 m几何曲线通过性能。
3.4 空车曲线通过安全性
铁水罐车在空车状态下以15 km/h通过半径为100 m、夹直线长度为19 m的S型曲线时,选取动力学性能较差的第三、六位轮对安全性指标曲线如图6、图7所示,所有轮对的安全性指标见表4。

图6 第三位轮对安全性指标

图7 第六位轮对安全性指标
由表4可知空车状态运行时,第三位和第六位轮对的安全性指标较高,但都小于标准规定的安全值,因此铁水罐车空车可安全通过该线路,但应对第三、六位轮对重点监测关注。

表4 空车曲线通过的安全性指标
3.5 重车曲线通过安全性
铁水罐车在重车状态下以10 km/h通过3.1节所述线路时,选取动力学性能较差的第三、六位轮对安全性指标曲线如图8、图9所示,所有轮对的安全性指标见表5。
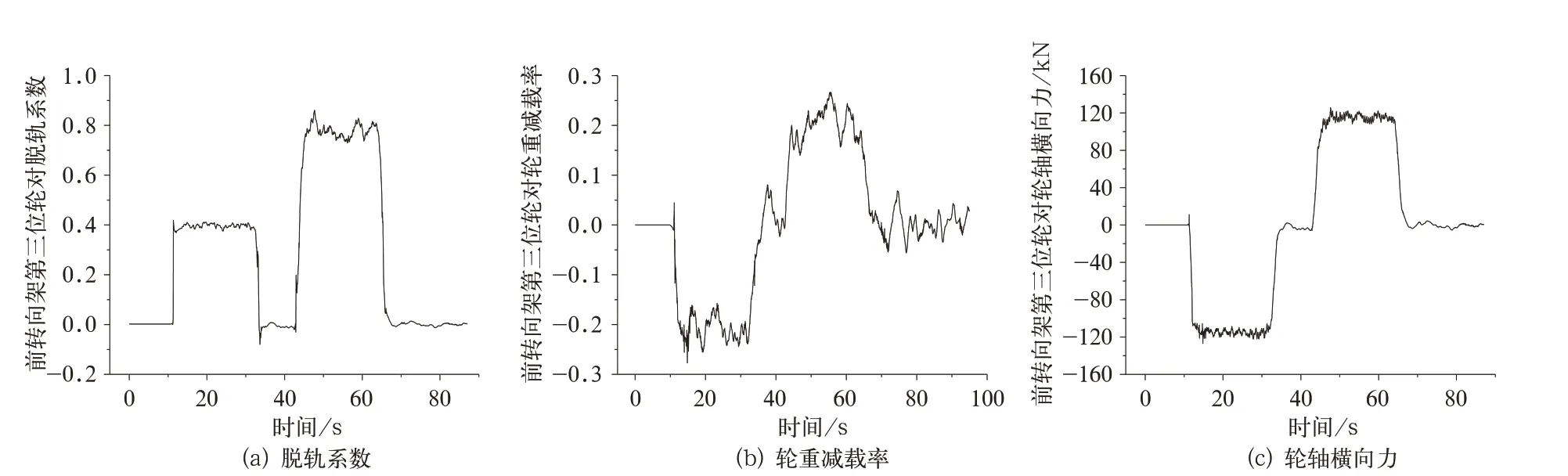
图8 第三位轮对安全性指标

图9 第六位轮对安全性指标
由表5可知重车运行工况下,第三位、第六位轮对的脱轨系数较大,其余指标较小。

表5 重车曲线通过的安全性指标
综上所述:文中所研究的140 t铁水罐车可以安全通过R100 m的S型曲线,分析中发现空、重车第三、六位轮对的脱轨系数相对较大,原因可能是此车辆运行速度低且载重大引起,因此实际运行中须重点监测,避免发生脱轨安全事故。
4 旁承间隙的合理范围
过小的旁承间隙会使车架上旁承与构架下旁承频繁接触,对车架和罐体产生较大的冲击,而过大的旁承间隙又使旁承在侧滚回复力矩不足时不能有效抑制铁水罐车的侧滚,因此以安全性指标为目标函数通过计算分析设置合理的旁承间隙。上下旁承垂向冲击力与间隙量的关系如图10所示。
由图10可 知,旁 承 间隙δ≤12 mm时,上下旁承多次冲击,当δ>12 mm时,上下旁承虽然频繁接触但未发生冲击。过大的冲击力不仅会降低车辆的动力学性能,也会对车辆各部件的强度造成较大影响。因此建议该铁水罐车的最小旁承间隙取13 mm。
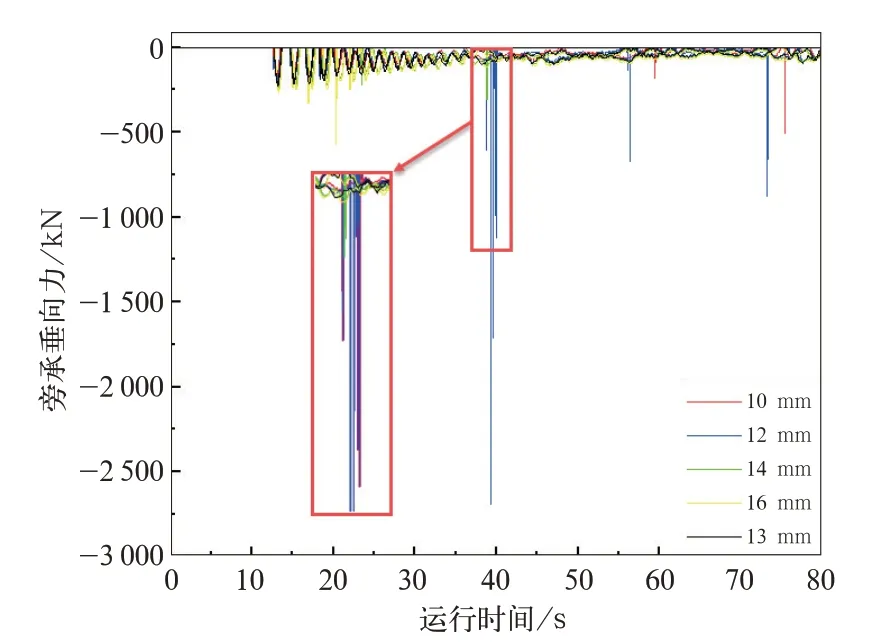
图10 旁承垂向力与间隙量的关系
铁水罐车重车通过S型曲线时,旁承间隙对其安全性指标的影响如图11所示,图中B1~B6表示该车辆的6个轮对。

图11 安全性指标与旁承间隙的关系
由图11可以看出:不同旁承间隙对轮重减载率影响较大,减载率随旁承间隙量的增大而显著增大,间隙量为20 mm时,轮重减载率最大为0.58,接近安全值0.6,而不同旁承间隙对脱轨系数和轮轴横向力影响较小。可见旁承间隙量增大主要是会加剧铁水罐车的侧滚,对横摆运动影响较小。综上分析可得:140 t铁水罐车旁承间隙的合理范围为13~20 mm。
5 结论
基于详细的多体动力学模型,研究了140 t铁水罐车的动力学特性,得到了如下结论:空、重车临界速度分别为62 km/h和69 km/h,运行速度裕量较大。当空、重车转向架处于最大偏斜或最大外移位置时,轮轨相对横移量均小于轮缘与钢轨的间隙,可满足R100 m几何曲线通过性能。此外,空、重车通过S型小半径曲线的安全性均满足GB/T 17426—1998,其中第三、六位轮对安全性指标较差,需要重点监测。旁承间隙对轮重减载率的影响相对较大,综合分析得到合理的旁承间隙范围为13~20 mm。
针对计算过程和仿真结果提出以下建议:应确保140 t铁水罐车具有恒定的牵引功率,避免因曲线阻力导致速度持续降低,以致不能通过S型曲线。上下心盘处保持较低的摩擦系数,尽量减少心盘处的摩擦阻力矩,从而减少轮轨磨耗。轨下基础的好坏是保持轨道具有良好运用条件的前提,因此铺设轨下基础时应考虑铁水罐车轴重大这一特点。

