北斗卫星钟差的CEEMDAN分解与周期项提取方法
梁益丰,许江宁,吴 苗,何泓洋
(海军工程大学 电气工程学院,武汉 430033)
全球卫星导航系统(Global Navigation Satellite System,GNSS)本身是高精度时间同步系统,实现定位与授时需要稳定的时间基准和高精度钟差预报技术。我国北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)于2020年7月全面开通,随着卫星数量和性能的不断提升,将卫星原子钟逐步纳入系统时间基准计算,最终实现完全基于卫星原子钟的系统时间基准生成,对于BDS安全性和性能提升有重要意义[1],因此有必要开展基于卫星钟差数据的时间尺度算法、钟差预报等相关技术研究。
由于运行环境复杂,卫星钟差数据通常包含趋势分量、多个周期分量、随机分量等成分。常用的最小二乘拟合趋势项方法不够准确,往往导致频率计算偏差,影响钟差预报精度和ALGOS类时间尺度算法中的频率预测[2];对拟合残差进行频谱分析时,由于噪声项和残留趋势项的干扰,可能导致周期辨识不准、幅值产生偏差[3];利用钟差或频率数据计算稳定度时,周期项通常会造成Allan偏差出现异常波动,不利于稳定度分析与噪声系数拟合,进而影响时间尺度算法中的权重选取[4]。因此,部分信号处理技术被先后应用于钟差数据分析:傅里叶变换将信号从时域转换到频域,以分离和区分平稳信号和噪声,但对于非平稳和非线性信号无效;小波变换可以在时域和频域中可视化信号,并且对非平稳信号有效,但其假设信号在小波窗口中平稳,且存在小波基选择问题[5];Kalman滤波被广泛用于钟差去噪和状态估计,但难以同时分解各种成分,且建模和实现较为复杂[6]。
经验模态分解(Empirical Mode Decomposition,EMD)是黄锷博士提出的一种自适应信号时频处理方法,适用于非线性非平稳信号的辨识、去噪与预测[7],该方法及其衍生模型近些年逐渐被应用于钟差数据处理。在频率稳定度方面,朱江淼利用集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)对原子钟频差数据进行降噪,效果优于小波阈值方法[8];惠恬将EMD与小波降噪相结合,一定程度上提升了频率稳定度[9];Aly I.Mostafa利用EMD提取随机分量,分别提升了单钟和钟组时间尺度的短期稳定度[10]。在周期项分析方面,伍贻威提出了原子钟模型和频率稳定度的系统性分析方法,并应用于地面氢钟数据分析[11];肖胜红提出了一种奇异谱分解与傅里叶带通滤波器相结合的周期项提取方法,提高了24 h周期项提取效率[12];李骁逸采取频谱分析确定周期大小与幅值,对提取周期项的钟差数据进行稳定度分析,表明周期项对频率的短期稳定度有显著影响[1]。上述分析大多集中于对钟差某一种成分的判定,或通过较多运算逐步分析各成分特征。同时,常用EMD方法存在模态混叠问题,在EMD基础上加入成对正负高斯白噪声的EEMD可以削弱模态混叠现象,然而其分量总会残留一定白噪声,影响后续分析与处理[13]。为此,TORRES等提出自适应噪声完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN)方法,在每次求解分量后重新给残值加入白噪声,然后逐次迭代求解[14],较好改善了模态混叠现象。
针对上述问题,本文提出一种能够同步提取钟差不同成分的“分解—辨识—重构”方法,在分析钟差主要特征的基础上,使用CEEMDAN方法完成数据分解,综合应用排列熵算法与t检验分析原理,对信号分量进行成分辨识,进而重构得到趋势分量、周期分量、随机分量,通过BDS钟差实测数据验证了方法的有效性和实用性。
1 BDS卫星原子钟钟差特性分析
1.1 卫星原子钟时差模型

以相位、频率、频漂三种参数组成的多项式模型是钟差的主要成分,也通常被应用于拟合趋势分量,周期分量与随机分量与趋势项相比数量级较小,但对稳定度的影响会逐渐积累。
1.2 各分量对稳定度的影响
以Allan方差为例,分析各分量在频率稳定度中的影响。文献[15]详细推导了噪声扩散系数与Allan方差的关系:


其中右边第1项为观测噪声,第4项为频漂,二者在对数Allan方差图中的斜率分别为-2和2。当周期表征较为明显时,Allan方差也将出现周期波动,表现为在某一平滑时间内的异常凸起。根据以上分析,常规噪声和频漂对频率稳定度的影响易于判断,然而卫星原子钟的多周期项会导致频率稳定度出现不确定因素,进而影响扩散系数拟合和性能分析。显然,将卫星钟差进行准确分解与重构十分必要,由于携带周期性波动的卫星钟差进行系统时间基准计算会将上述波动引入系统时间,因此未消除周期项的钟差数据不应纳入系统时间基准计算。
2 基于CEEMDAN分解的信号分析方法
2.1 CEEMDAN分解原理

计算去除第二个模态分量后的残差:
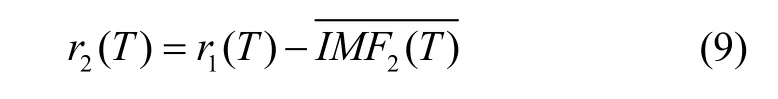
重复上述步骤,直到获得的残差信号为单调函数,不能继续分解,算法结束。此时得到的本征模态分量数量为K,则原始信号()x T被分解为:
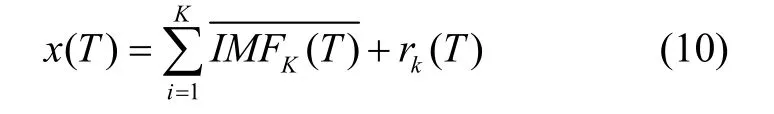
由于加入白噪声方式的改进,CEEMDAN在较小的平均次数下就能达到极小的重构误差,完备性优于EEMD方法,也因此具备更少的平均次数和更快的计算速度[14]。此外,EEMD分解还可能出现多个幅值很小的低频IMF分量,CEEMDAN方法能够改善此现象。其具体分解流程如图1所示。

图1 CEEMDAN分解流程Fig.1 The CEEMDAN decomposition process
2.2 排列熵算法
排列熵算法可以衡量系统复杂度,检测时间序列随机项突变的方法,计算简单快速,鲁棒性强,已被广泛应用于非线性数据处理与分析[16]。第i个模态分量IMFi(T)的排列熵值求解过程如下:
步骤1:对长度为N的IMFi(T)进行m维相空间重构,生成K×m的矩阵IMF:

排列熵值大小表示时间序列随机程度:熵值越小,说明时间序列越简单、规则;熵值越大,则时间序列越复杂、随机。由此,引用该算法定性分析钟差信号中的信号主导分量和噪声主导分量。
2.3 模态分量特征分析
尽管排列熵算法能够有效辨识信号与噪声主导分量,但因为卫星工作环境复杂,经分解的钟差数据临界模态仍然可能存在多种信号。为此,引用文献[17]所采取的t检验方法对模态分量进行特征分析,以确保重构信号的准确性。
t检验是用t分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著。分析CEEMDAN原理可知,其IMF分量应满足上、下包络线相对于时间轴局部对称。则高频IMF分量的上下包络线基本由众多的信号峰值点连接得到,对称的包络线意味着IMF数据基本对称,数据均值趋近于0;低频IMF信号周期大,包络线由少量峰值插值获取,与原信号趋势走向关联度较低,所以信号分量并不对称,很难保证均值为0。由此,将分解得到的K个IMF做高低频区分。不妨假设IMF1为指标1,IMF1+IMF2为指标2,以此类推,前i个IMF的和为指标i,自指标1开始计算均值,对其是否显著区别于0进行t检验分析,当显著区别于0时停止计算。t检验统计量为[17]:

2.4 钟差数据分解与重构流程
综合卫星钟差数据处理、信号分解、模态分量特征分析等过程,给出钟差数据分解与重构流程如图2所示,具体步骤如下:
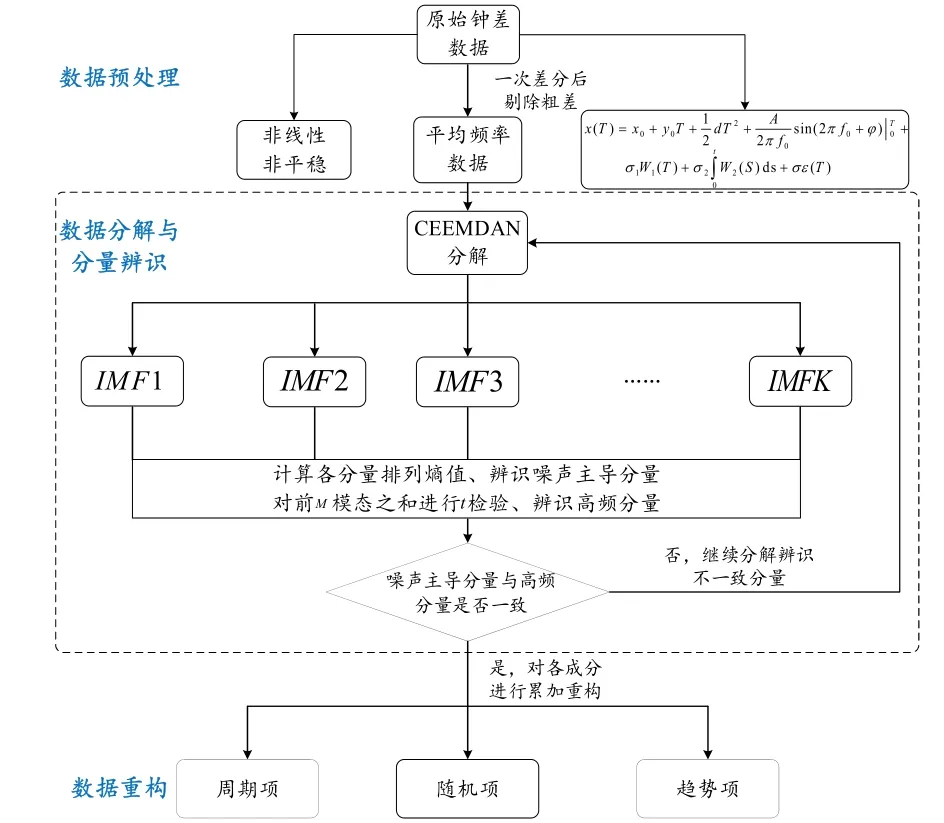
图2 钟差数据分解与重构流程图Fig.2 Flow chart of clock difference data decomposition and reconstruction
步骤1:钟差数据预处理,利用中位数探测法完成粗差剔除,并进行平滑插补。考虑到频率数据有效位次多于钟差数据,因此做一次差分求平均频率()y T;
步骤2:将()y T通过CEEMDAN分解为K个本征模态分量,按照高频到低频顺序排列;不失一般性,分解时设置附加噪声标准差与()y T标准差之比为0.2,信号平均次数为100次;
步骤3:计算各个模态的排列熵值,根据相邻值的变化确定信号主导分量和噪声主导分量(一般第K个模态为趋势项,此处通过排列熵进行核验);
步骤4:对前M(M≤K)模态之和进行t检验,根据其均值是否显著区别于0判断高频和低频分量;
步骤5:当排列熵确定的噪声主导分量和t检验得到的高频分量相同时,直接判定为钟差随机分量;若存在辨识不一致分量,则继续分解相应模态,直至达到一致,以确保周期信号与噪声信号完全分离;
步骤6:对被判定为随机分量的模态累加得到随机项,除随机项和趋势项之外的模态累加得到周期项,数据分解与重构完成。
3 算例分析
采用德国地学研究中心(Deutsches geoforschungs zentrum,GFZ)发布的BDS卫星精密钟差数据,选择数据连续性较好的C04、C13、C37、C40卫星原子钟,包含GEO(C04)、MEO(C37)、IGSO(C13与C40)轨道类型,铷原子钟(C04、C13、C37)和氢原子钟(C40)钟型,取2021年7月4日至7月13日共计10天2880个数据点,历元间隔为5 min。
3.1 钟差数据分解与重构效果
以C37为例展示数据分解与重构的完整过程,其平均频率数据经CEEMDAN分解得到11个IMF,各分量与原始数据图如图3所示。原始信号与IMF之和做差,其残差均方根为6.24 ×10-28,说明C37平均频率数据得到了完全分解。计算各模态排列熵值,IMF11计算结果为0.0820,表明几乎不含波动分量,因此直接作为趋势项。其余分量排列熵如图4所示。
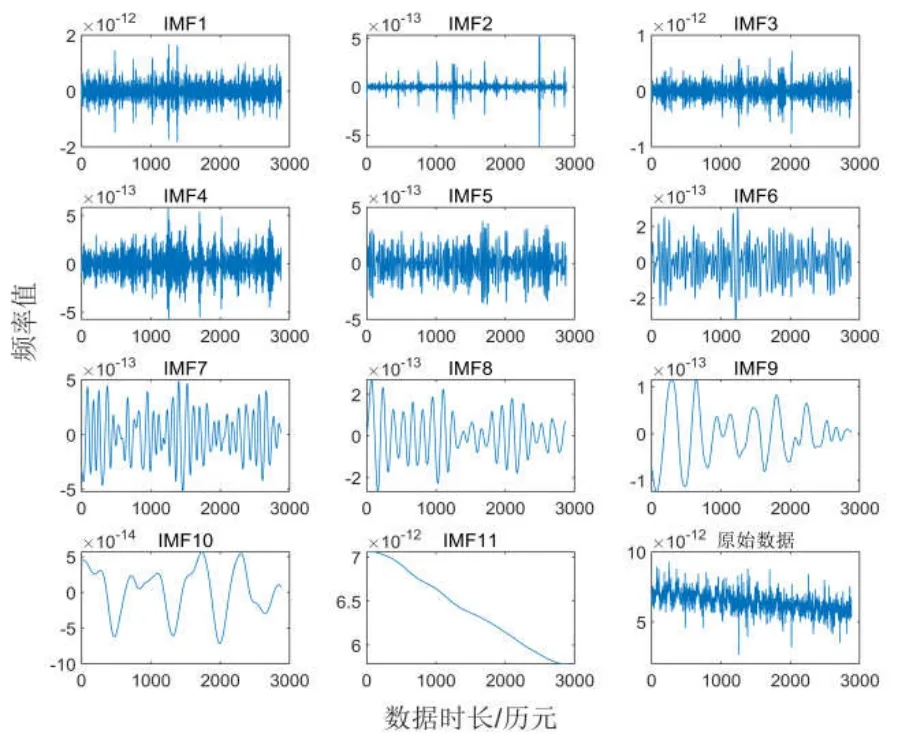
图3 C37卫星原子钟频率数据CEEMDAN分解结果Fig.3 CEEMDAN decomposition results for the C37 satellite clock frequency data

图4 C37卫星原子钟各频率模态排列熵值Fig.4 The entropy of each mode for C37
由排列熵显著拐点初步判断,第1~6个IMF为噪声主导分量,第7~10个IMF为信号主导分量。此外,t检验也在指标7处显著不为0,据此分别将第1~6个IMF相加得到高频分量、第7~10个IMF相加得到低频分量,完成信号重构如图5所示。
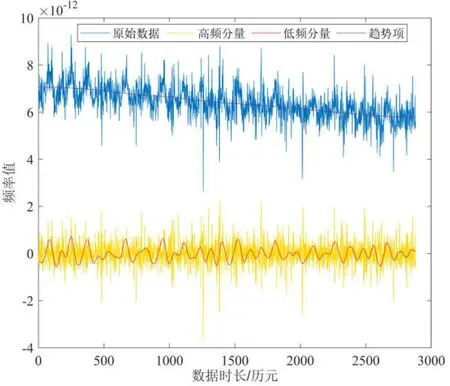
图5 C37卫星原子钟各分量重构结果Fig.5 Results of each component reconstruction for C37
在分析过程中,C04原子钟经一次分解后的排列熵与t检验在8IMF分量处结果不同、进行了二次分解,一方面反映出排列熵和t检验结果大多相符,另一方面也说明了本文综合分析策略的合理性与必要性。4颗卫星原子钟主要成分重构结果如图6所示。
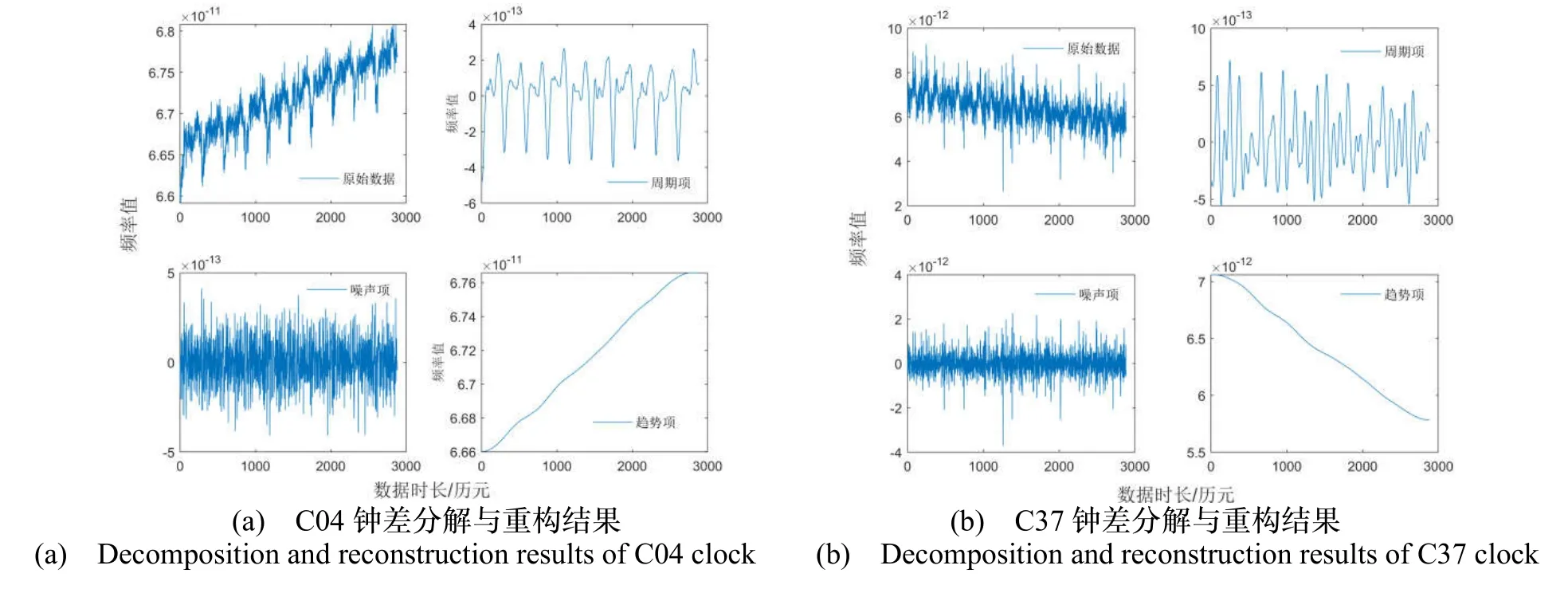

图6 4颗卫星原子钟各分量重构结果Fig.6 Results of each component reconstruction for four clocks
通过图6可以得到,4颗原子钟频率变化趋势分别为递增(C04)、递减(C37)与近似平稳(C13、C40),CEEMDAN方法能够准确分解得到各种变化特点的趋势项,即使近似平稳的微小波动也能跟踪;各原子钟都含有多个规律周期,噪声项呈无规律变化,数值普遍大于周期项。不同原子钟初步对比结果表明,C37原子钟频率值小于C04与C13,但周期分量显著高于其余卫星原子钟,表明MEO卫星受周期项影响更为明显;C40原子钟频率值、周期项、噪声项均为最小,反映了氢原子钟的优良性能。
3.2 周期项特征分析
现有研究已经对GNSS卫星原子钟长期特性进行了较全面的分析,表明其包含与系统轨道周期密切相关的周期项。例如,BDS卫星原子钟的主周期项通常有24 h、12 h、8 h、6 h,Galileo卫星原子钟的主周期项约为14 h和7 h[18,19]等(轨道周期14.039 h)。当特性分析时间较长时,随时间累积的周期项通常在频谱图中呈现较明显的波峰,但当特性分析时间较短时,钟差拟合残差和噪声可能会导致频谱图出现局部峰值。以上结论可为频谱分析提供一定参考。
通过常用二次多项式拟合相位得到相位拟合残差,以CEEMDAN分解重构得到频率周期数据,然后分别进行快速傅里叶变换获得卫星原子钟的周期特性。4颗卫星原子钟频谱图如图7所示,可以看出,BDS各类卫星原子钟均存在多种周期项,对比拟合残差和提取周期项频谱分析结果,主要结论如下:

图7 4颗卫星原子钟周期项分析结果Fig.7 Analysis of periodic term of four clocks
(1)二次多项式拟合方法难以完整提取钟差趋势项、同时包含大量高频分量,其残存趋势分量导致频谱图靠近y轴处出现不规则峰值,高频分量导致主周期项右侧出现大量不规则波动;本文方法提取的周期信号,其低频部分未出现不规则峰值、主周期项特征明显,且高频处基本没有异常波动,表明提取所得周期项基本不含趋势和随机分量,提取效果较好;
(2)主周期变化方面,C04原子钟拟合残差与所提取周期项在峰值数量与主周期方面区别较大,其拟合残差周期项排序依次为24 h、12 h、6 h、8 h、4.8 h、4 h、3.43 h等,所提取周期项主周期为12 h、24 h、8 h、6 h(前两项幅值接近),由于周期主要因卫星运行导致、拟合残差的高频周期项数值大多是主周期项的公约数,合理推测:拟合残差的高频周期项可能为周期信号在随机分量干扰下耦合产生。而本文方法有效分离了周期信号与随机信号,避免了耦合现象;
(3)不同类型卫星原子钟的主周期因轨道区别而有所差异,GEO卫星钟主周期为12 h、24 h、8 h、6 h,MEO卫星钟主周期为12 h、8 h、6 h。对于IGSO卫星,以拟合残差分析得到的C13原子钟主周期为24 h、6 h,C40原子钟主周期为24 h、8 h,根据周期项产生原因,相同轨道的卫星原子钟周期项通常一致,说明二者拟合残差数据中的多余信号干扰了频谱分析结果,部分周期项被淹没,这也是6 h、8 h波峰附近出现较多不规则信号的主要原因。以所提取的周期项分析时,二者主周期项均为24 h、8 h、6 h,其中C13所提取6 h周期项左侧仍然存在多余信号,可能是由多周期项功率谱旁瓣所致,但相比拟合残差频谱图已有明显改善,提取效果将在3.3节得到进一步验证。此外,C37原子钟周期项幅值占比最大、C40原子钟周期项幅值占比最小,反映出MEO卫星受到周期项干扰最大,该现象可能是由于MEO卫星与地球运行非同步所致;GEO和IGSO卫星受周期项影响相对较小,其中IGSO氢原子钟最小。
3.3 频率稳定度分析
结合卫星原子钟时差模型和各分量特征,对BDS卫星原子钟的频率稳定度展开研究,以进一步检验本文方法提取周期项的准确性,并定量分析周期项对卫星原子钟稳定度的影响。分别计算4颗卫星原子钟原始数据、周期项数据、去除周期项数据的Allan偏差,如图8所示。可以看出,4颗卫星钟原始稳定度曲线都存在异常凸起,与所提取周期项的稳定度曲线吻合,说明本文所提取的周期项能够准确表征对稳定度的影响,在去除周期项后,各原子钟在不同平滑时间内的稳定度指标均得到一定提高。对于不同轨道类型的原子钟,MEO卫星原子钟周期项对稳定度的影响最明显,峰值约为2.21×10-13,IGSO氢原子钟周期项影响最小,峰值约为3.02 ×10-14;MEO卫星钟周期项对万秒稳的影响最为明显,其余卫星钟的20000~40000 s稳定度受周期项影响最大,与相应主周期项显著相关。但是不论何种轨道类型、何种原子钟类型的卫星,校正后的稳定度曲线都显著改善了原稳定度曲线的异常凸起。

图8 4颗卫星原子钟周期项分析结果Fig.8 Analysis of periodic term for four clocks
将周期项提取与稳定度分析结果总结如表1所示,所有卫星的频率稳定度性能都获得了显著的提升,万秒频率稳定度提升幅度依次为14.0%、47.2%、17.6%、7.8%,平均为21.6%。其中,C37卫星提升效果最为显著,万秒频率稳定度由2.44 ×10-13提升到1.29 ×10-13,其余卫星原子钟稳定度提升最显著的采样时间主要在20000~40000 s之间,因此万秒稳改善程度相对不明显。对于MEO卫星数量较多的BDS-3系统,这种改进明显有利于时间基准的建立与维持。
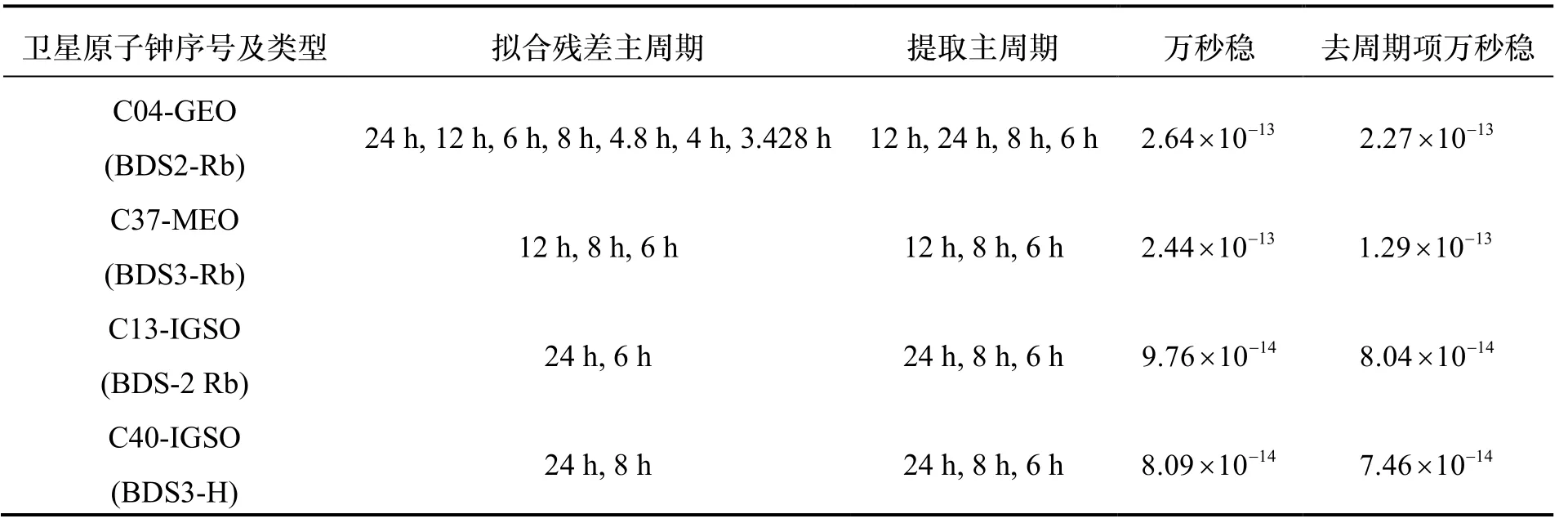
表1 卫星原子钟数据综合分析结果Tab.1 Comprehensive analysis of satellite clock data
4 结论
分析了卫星钟差不同分量对于频率稳定度的影响,阐述了钟差数据分解与重构的必要性,提出了综合CEEMDAN分解、排列熵原理和t检验的BDS卫星钟差信号分解与周期项提取方法。基于4颗不同类型BDS卫星原子钟的实测数据展开分析,结果表明,本文方法能够有效、准确地分解卫星原子钟趋势分量、周期分量与随机分量,便于各种成分的定量分析和原子钟性能评估;所提取周期分量的频谱图相比常规多项式拟合残差频谱图更为清晰、周期特征更加明显;对提取周期分量进行稳定度分析,其稳定度曲线与钟差稳定度曲线的异常凸起吻合度较高,进一步验证了本文方法的有效性。去除周期分量后,4颗BDS卫星原子钟的万秒稳平均提升21.6%,将有助于高稳定度时间基准的生成与维持。
实测数据分析部分主要展示了BDS卫星钟差分解与周期项提取效果,但通过研究过程不难看出,基于钟差信噪分离的思路与方法在频率和钟差预报、原子钟数据降噪、原子时算法等方面都有广阔的应用前景[20]。

