基于非0比特个数特征的冗余转移图像加密安全性分析

罗雅婷 和红杰 陈 帆 屈凌峰

1(西南交通大学信息科学与技术学院 成都 611756) 2(西南交通大学计算机与人工智能学院 成都 611756)

传统信息隐藏技术[1]在数据嵌入过程中会对载体信息造成不可逆转的失真，很难满足法庭举证、军事机密等应用场合.可逆信息隐藏(reversible data hiding, RDH)[2-4]技术在隐藏秘密信息的同时，可以无损恢复载体信息，很好满足了上述应用需求.随着互联网技术的不断发展，图像、视频等数字媒体经常上传云端保存或应用，其携带的秘密、隐私等信息存在泄露的安全风险，推动了加密域可逆信息隐藏(reversible data hiding in encrypted image, RDH-EI)技术的发展[5-7].RDH-EI技术首先对原始图像加密，再将重要的秘密信息嵌入加密图像中，接收者根据密钥提取秘密信息，基于密钥无失真恢复原始图像.RDH-EI保证了图像恢复的可逆性与数据传输的安全性，已成为云计算的研究热点之一.

RDH-EI发展至今，隐藏容量、可逆性与图像解密质量等性能指标都有了很大的提高.以嵌入容量为例，一些平滑图像的最高嵌入容量达到了2.03 bpp[8]，与早期算法不足0.01 bpp[5]相比，提高了将近200倍.与隐藏容量相比，RDH-EI技术的安全性研究起步较晚.如果RDH-EI的图像加密算法存在安全隐患，则上传云端保存的加密图像在恶意或无意攻击下可能导致原始图像内容的信息泄露.因此为了保证图像内容的安全，图像加密算法的安全性对RDH-EI技术至关重要.

传统的RDH-EI图像加密主要包括流密码异或加密[9-13]与置乱加密[14-18].流密码异或加密将每个像素转换为8 b的二进制，分别与随机产生的二值密钥流异或再转成十进制，改变像素值以实现图像加密.2017年Khelifi[19]提出利用多幅密文图像各个位平面的位之间的水平冗余与垂直冗余来估计流密码密钥的唯密文攻击.也就是说，在密钥重用条件下，流密码异或的图像加密方法存在信息泄露的安全风险.另一方面，基于置乱的图像加密算法设计有效提高了嵌入容量，如文献[17]使用块置乱加密的嵌入容量高达1.71 bpp.然而文献[20-22]的研究表明，无论置乱的单位是比特还是像素，均存在信息泄露的危险.如文献[21]，针对改变像素位置的加密算法，提出一种利用像素值取交集的已知明文攻击方法.查看明文图像(i,j)位置处的像素值，在其对应的密文图像中查找该像素值的所有像素位置(称“1对明-密文图像”)，再利用多对明-密文图像得到的位置集合取交集，可确定(i,j)位置的最终置换位置，即像素置乱密钥.因此，单纯地改变像素值或像素位置的加密算法并不安全.为了提高图像加密的安全性，RDH-EI技术设计将像素值改变与像素位置改变相结合的图像加密算法，如流密码异或与像素置乱相结合(称“块异或-置乱”)[3,9]、调制与块置乱相结合(称“块调制-置乱”)[23-25].这类图像加密方法能有效抵抗文献[19-22]的攻击，以提高安全性为代价减少了原始图像的冗余，算法的嵌入容量不高.同时文献[26-27]发现， 加密后的密文图像仍然保留了明文图像块中部分像素的相关性，很难抵抗针对性的已知明文攻击[26-27].

兼顾安全性与嵌入容量，Liu等人[17]提出一种基于冗余空间转移(redundant space transfer, RST)的加密算法.该算法中位平面置乱将原始图像高位平面的冗余转移到低位平面，提高了嵌入容量的同时改变了像素值；然后块置乱与块内像素置乱改变了像素位置，有效提高了抵抗文献[19-22]攻击的能力.然而该算法在位平面置乱时，是以整个图像块为单位进行置乱的，保留了位平面间的冗余，为文献[28-29]利用位平面比特1的个数重构位平面提供了可能.同时位平面置乱密钥空间较小(3!×5!)，使利用穷举法借助直方图距离估计位平面置乱密钥成为了可能[30].一旦位平面置乱密钥被估计出来，攻击者就能重构原始图像的像素值，从而易受现有的已知明文攻击[21-22].Qin等人[8]提出了一种基于改进冗余转移图像加密(称“Qin加密算法”)的RDH-EI 算法，有效提高了位平面置乱的密钥空间.Qin加密算法首先将图像分块，对每个图像块采用不同的位平面置乱密钥，使位平面置乱的密钥空间从(3!×5!)提高到(3!×5!)k，其中k为图像包含的图像块

总个数.Qin加密算法以图像块为单位对位平面置乱，改变了位平面比特0,1的比例，同时密钥空间增大，大大增加了利用穷举法[30]估计位平面置乱密钥的难度，有效提高了抵抗文献[28-30]中已知明文攻击的能力.

正如文献[29]指出，块内位平面置乱与块内像素置乱呈弱密钥性，块置乱密钥是冗余转移加密算法的关键.如果能利用原始图像转移至加密图像中的“冗余”直接估计块置乱密钥，进一步估计位平面置乱密钥，是否可能导致信息泄露是一个值得研究的安全问题.为验证Qin加密算法的安全性，本文提出一种针对冗余转移加密算法的已知明文攻击方法，主要贡献有3方面：1)分析Qin加密算法的特点，定义图像块的非0比特个数(non-zero-bit number, NZBN)特征，指出加密前后图像块NZBN特征保持不变的特点；2)提出一种基于图像块NZBN特征的块置乱密钥估计的已知明文攻击方法，与现有方法不同，该攻击方法无需恢复位平面，先估计块置乱密钥，再估计每个图像块的位平面置乱密钥；3)为实现更精准的置乱密钥估计，给出多对已知明文攻击方法.

1 Qin加密算法与特性分析

本节通过对Qin加密算法[8]进行简述，分析Qin加密算法自身特性，给出Qin加密算法存在安全隐患的原因.

1.1 Qin加密算法简述

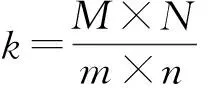
步骤1.块内置乱.块内置乱包括位平面置乱与像素置乱.明文图像X={Xi|i=1,2,…,k}在经过块内置乱后得到图像Z={Zi|i=1,2,…,k}的步骤如下：

(1)

(2)

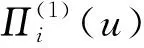
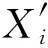
(3)

(4)

1.2 Qin加密算法特性分析

本文引言中对无法重构位平面从而无法估计位平面置乱密钥进行了阐释，而文献[29]指出块内像素置乱密钥空间小的特性，并通过实验验证块内像素置乱密钥的弱密钥性.因此破解Qin加密算法最重要的是估计块置乱密钥.而块置乱密钥估计的重要步骤是寻找块置乱前后图像块恒定不变的特征.研究发现，Qin加密算法中图像块的“非0比特个数”特征在块置乱前后保持一致，这为估计块置乱密钥提供了可能.

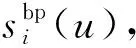
(5)

(6)

(7)

图1示出1个2×2大小的明文图像块Xi与经过块内置乱的图像块Zi.如图1所示，无论明文图像块的位平面被置换到哪一位平面，在图像块Zi中总能找到可能被置换到的位平面序号，通过比较图像块的位平面NZBN可以实现.如图像块Xi的8个位平面NZBN组成的集合为{1,3,3,1,1,1,3,1}，而图像块Zi的位平面NZBN集合为{3,1,1,3,1,1,3,1}.对比集合中的各个元素可发现图像组成位平面NZBN的集合相同.同样地，无论明文像素被置换到哪一位置，通过比较图像块的像素NZBN集合，在Zi中总可以找到可能被置换到的像素位置.如明文图像块Xi的像素NZBN组成的集合为{3,3,4,4}，而图像块Zi的像素NZBN集合为{4,4,3,3}.只要图像块是经过Qin加密算法中块内置乱得到的，那么块内置乱前后图像块的位平面NZBN集合与像素NZBN集合保持不变.

Fig. 1 The image block before and after the block scrambling图1 块内置乱前后的图像块

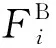
(8)

(9)

那么构成图像块Xi的NZBN特征Fi为

(10)

根据NZBN特征的定义，发现图1中明文图像块Xi与块内置乱后的图像块Zi的位平面NZBN特征完全相同，且像素NZBN特征完全相同.基于这一发现，本文推出性质1～3：

性质1.像素置乱不改变位平面非0比特个数.

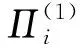
(11)

图像块Zi的位平面NZBN为

(12)

证毕.

性质2.块内置乱前后，图像块位平面非0比特个数特征保持不变.

证明.由式(11)与式(12)可得，图像块Zi中第u个位平面的位平面NZBN与图像块Xi位平面NZBN的关系为

(13)

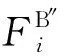
(14)

证毕.

性质3.块内置乱不改变图像块的像素非0比特个数特征.

证明.由式(11)计算图像块Zi在位置j处的像素NZBN

(15)

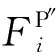
(16)

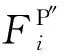
证毕.

以上3个性质揭示了Qin加密算法块内置乱的特点，这些特点使加密算法存在泄露置乱密钥的安全风险，分析如下：

1) 块内置乱不改变图像块的NZBN特征(性质2,3)，使得根据明文图像X与密文图像Y估计块置乱密钥成为可能；

2) 像素置乱不改变图像块的位平面NZBN(性质1)，使得估计位平面置乱密钥成为可能.

2 基于非0比特个数特征的已知明文攻击

如果攻击者得到1对或多对明-密文图像，本文利用NZBN特征估计不同置乱密钥的过程包括3个主要步骤：1)基于图像块NZBN特征等价划分的块置乱密钥估计；2)图像块的位平面置乱密钥估计；3)多对明-密文图像下的置乱密钥估计方法.

2.1 块置乱密钥估计

如果攻击者得到1对明-密文图像{X,Y}，寻找密文图像Y={Yi|i=1,2,…,k}在明文图像X中的位置，就是块置乱密钥估计的过程.

如图2所示，设有明文图像X，在经过Qin加密算法加密后，产生密文图像Y.若使用穷举法估计块置乱密钥，共有6!种可能，且无法确定块置乱密钥估计正确的判定条件.

基于定义的NZBN特征划分图像块，就是文献[30]中定义的等价划分.与文献[30]不同的是，本文等价划分的标准是图像块的NZBN特征.基于NZBN特征对图像块等价划分后，6个明文图像块划分在5个等价集中，如图2(c).由1.2节分析得到的图像块NZBN特征恒定不变性可知，明文图像X和密文图像Y得到的等价集一定相同.根据同一NZBN特征等价集中的明-密文图像块序号，即可估计块置乱密钥.

以图2为例，密文图像块Y6的NZBN特征与明文图像块X1的NZBN特征完全相同，所以估计的块置乱密钥集合为K(6)={1}，且等价集与图像块个数是唯一对应的，因此当前图像块的块置乱密钥估计正确率为1；而对于密文图像块Y3，与明文图像块{X2,X6}具有相同的NZBN特征，估计的块置乱密钥集合K(3)={2,6}，由于等价集对应2个图像块，无法确定Y3是由明文图像块X2还是X6置换得到，因此当前图像块估计的块置乱密钥正确率为1/2.

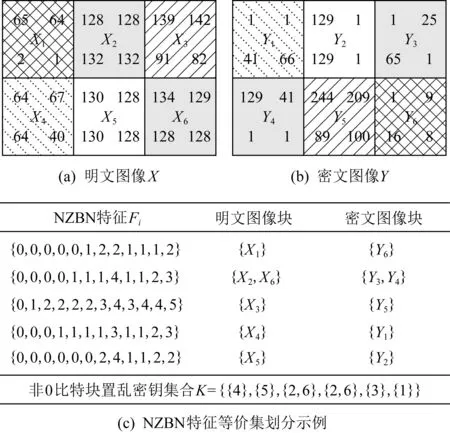
Fig. 2 An example of dividing image blocks based on NZBN feature图2 基于NZBN特征划分图像块的示例

从之前图像块的查找范围为6!到现在2!，基于NZBN特征等价划分图像块后有效缩减了图像块的查找范围，且具有密钥估计正确的判定条件，可用于块置乱密钥的估计.为验证本文已知明文攻击方法估计块置乱密钥的有效性，基于NZBN特征的块置乱密钥集合估计方法描述如算法1.

算法1.基于NZBN特征的块置乱密钥集合估计算法.

输入：明文图像X、密文图像Y；

输出：块置乱密钥集合K.

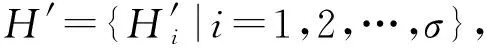
② forH和H′中的每一个元素(i=1,2,…,σ) do

③ 获取明文图像块序号的集合A=H(i)；

④ 获取密文图像块序号的集合B=H′(i)；

⑤ forB中的每个元素v(v=1,2,…,τi) do

⑥ 被置换到的位置集合K(B(v))=A；

⑦ end for

⑧ end for

⑨ returnK.

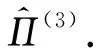
2.2 位平面置乱密钥估计

根据2.1节估计的块置乱密钥，将密文图像Y恢复成块间置乱前的图像Z.本文1.2节的性质1给出了位平面置乱密钥估计的依据，估计位平面置乱密钥的具体步骤见算法2.

算法2.位平面置乱密钥集合估计算法.

输入：明文图像X、块间置乱前的图像Z；

输出：位平面置乱密钥集合Q.

① 将M×N大小的图像X和Z分别分解成k个m×n大小的不重叠图像块；

② for 每个图像块ido

④ for 位平面j(j=1,2,3) do

⑥ end for

⑦ for位平面j(j=4,5,…,8) do

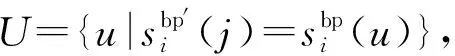
⑨ end for

⑩ 第i个图像块的位平面置乱密钥集合Qi={Qi(j)|j=1,2,…,8}；

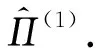
2.3 多对已知明文攻击

1对已知明文攻击是指根据已经得到的1对明文图像与其对应的密文图像估计加密密钥的已知明文攻击方法.多对已知明文攻击是指根据2对或2对以上的明文图像与其对应的密文图像估计加密密钥的已知明文攻击方法.

2.1节和2.2节分别介绍了1对已知明文攻击下的块置乱密钥与位平面置乱密钥估计方法.在分块较小或明文图像比较平滑时，仅1对明-密文图像估计的块置乱密钥正确率不高.如果无法正确恢复块置乱，就无法利用明-密文图像块的位平面NZBN估计位平面置乱密钥.同时，在1对已知明文攻击下估计的置乱密钥不是单值的，是1对多的，为了得到更精准的置乱密钥估计值，本节给出了多对已知明文攻击方法，具体实现方法如下：

步骤1.获得α对密钥集合.参照2.1节与2.2节的置乱密钥估计方法，分别得到块置乱密钥集合K与位平面置乱密钥集合Q.其中第i对已知明文估计的块置乱密钥集合为Ki，位平面置乱密钥集合为Qi.

步骤2.α对密钥取交集.α对已知明文估计的块置乱密钥集合为K=K1∩K2∩…∩Kα，位平面置乱密钥为Q=Q1∩Q2∩…∩Qα.

利用多对明-密文图像的已知明文攻击方法有效提高了置乱密钥正确率，解密出更清晰的图像，且解决了分块较小时本文提出的已知明文攻击方法不能破解置乱密钥这一问题，具体验证实验详见3.3节.

3 实验结果及分析

采取5幅大小为512×512的灰度图像(如图3所示)和使用Qin加密算法加密后的密文图像用于实验.本节首先分析自然图像中图像块NZBN特征的各异性；然后验证基于NZBN特征的1对已知明文攻击的有效性；接着分析多对已知明文攻击的算法性能；最后讨论已知明文攻击的算法时间复杂度.

Fig. 3 Five plaintext images图3 5幅明文图像

3.1 NZBN特征的各异性

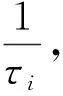
由于自然图像的不同，在基于NZBN特征等价划分后的等价集个数σ与每个等价集中包含的图像块个数τi均不相同.尤其是当分块大小较大时，每个等价集中的τi个数较少甚至为1，有较高概率估计出完全正确的块置乱密钥，是由于NZBN特征具有各异性.图像块NZBN特征的各异性是指，不同图像块的NZBN特征相同的概率较小.为了分析自然图像NZBN特征的概率分布情况，这里给出描述概率分布的参数：

1)τi=1的等价集个数占等价集总数σ的比例称为唯一等价集占比Ho，计算方法为

(17)

其中t为τi=1的等价集个数.

2) 所有Hi(i=1,2,…,σ)中的最大图像块个数τmax取值为

τmax=max{τ1,τ2,…,τσ}.

(18)

3) 文献[30]估计的块置乱密钥理论正确率ρ′为

(19)

为了分析不同图像的图像块NZBN特征的概率分布情况，分别以2×2,3×3,4×4，8×8分块大小的图像为例，将图3中的前4幅测试图像基于NZBN特征等价划分图像块，统计等价划分后的等价集总数σ、唯一等价集占比Ho、最大图像块个数τmax与块置乱密钥理论正确率ρ′，结果如表1所示:

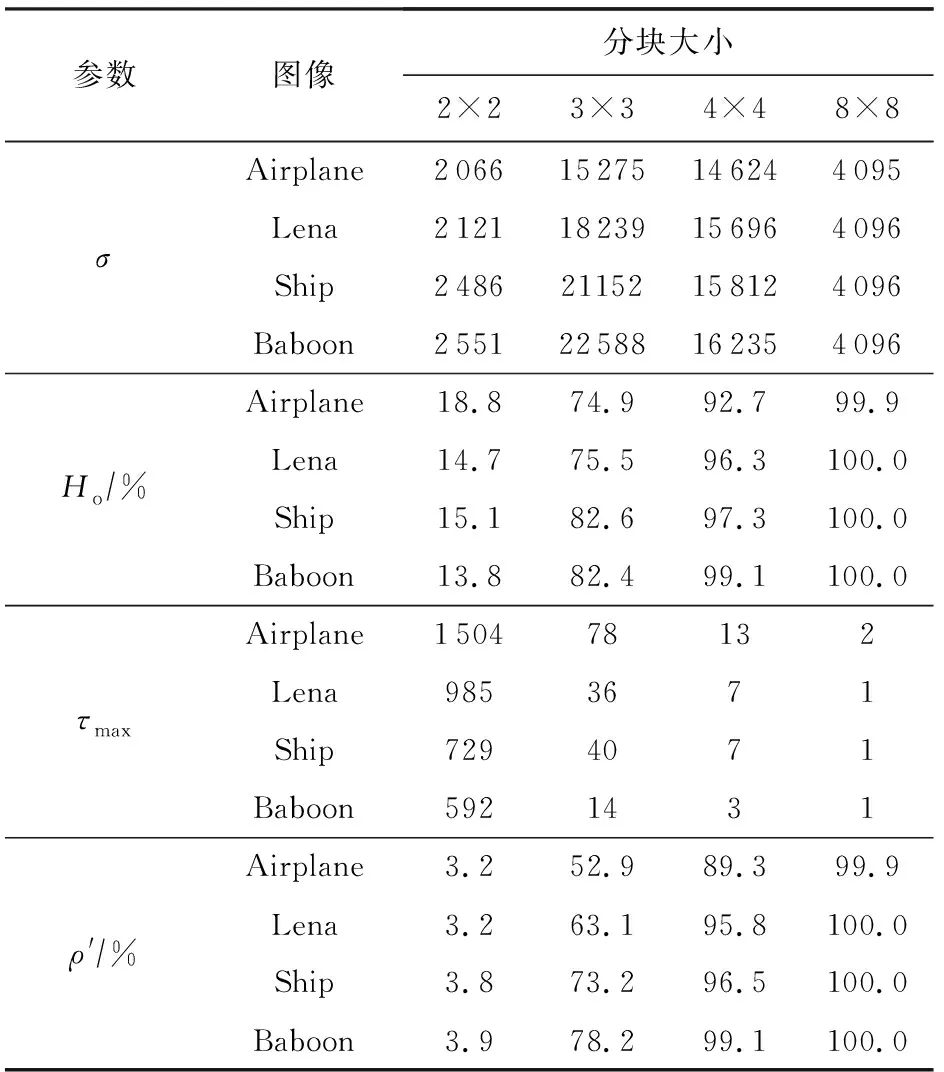
Table 1 NZBN Feature Distribution of Different Images and Different Blocks

表1显示，随着图像分块的增加，ρ′也增加，说明越来越多的图像块被划分在不同的等价集中；同时，Ho增加，说明NZBN特征等价集中τi=1的等价集个数增加，即大部分图像块的NZBN特征是各不相同的；而τmax减少，说明即使有部分图像块具有相同的NZBN特征，但随着图像分块的增加，具有相同特征的图像块个数在减少.ρ′,Ho，τmax的结合，验证了NZBN特征的各异性.

当分块大小为3×3时，图像块NZBN特征等价集中有超过70%的等价集包含的图像块个数τi=1.当分块大小增加到8×8时，自然图像中的唯一等价集占比Ho基本达到100%.也就是说，随着图像分块的增加，等价集中τi=1的等价集个数增加，τi>1的等价集个数减少，增强了NZBN特征各异性也为块置乱密钥的估计带来了可能.以3×3分块大小为例，随着图像纹理复杂度的增加，ρ′增加，等价集总数σ增加，同时Ho增加，这说明更多的图像块与NZBN特征是唯一对应的，τi>1的NZBN特征个数在减少，增强了NZBN特征的各异性.正是由于NZBN特征存在各异性，不同的图像具有不同的NZBN特征，使得块置乱密钥估计成为可能.3.2节将设计实验验证本文提出的基于NZBN特征对于块置乱密钥估计的有效性.

3.2 1对已知明文攻击

本部分首先分析不同分块大小下本文已知明文攻击的块置乱密钥估计性能，然后给出位平面置乱密钥的估计性能.

3.2.1 块置乱密钥的估计

3.1节对NZBN特征的各异性进行了分析，τi=1的等价集说明，具有这一NZBN特征的图像块是唯一的，因此可确定唯一的块置乱密钥.由于自然图像的不同，图像块的NZBN分布不同，Ho也不尽相同，因此估计的块置乱密钥正确率也不同.以图3中前4幅明文图像与其对应的密文图像为例，测试不同分块大小下使用1对已知明文攻击估计的块置乱密钥解密密文图像Y，得到块置乱前的图像Z′，如图4所示.

Fig. 4 Results of decrypted block scrambling under a pair of known-plaintext attack图4 1对已知明文攻击的解密块置乱结果

图4显示解密块置乱后的图像仍然是1幅噪声图像，为了直观地分析本文提出的NZBN特征对于块置乱密钥估计的重要意义，给出块置乱密钥估计正确率的计算方法.

(20)

分别计算4对测试图像所估计的块置乱密钥正确率，如表2所示：

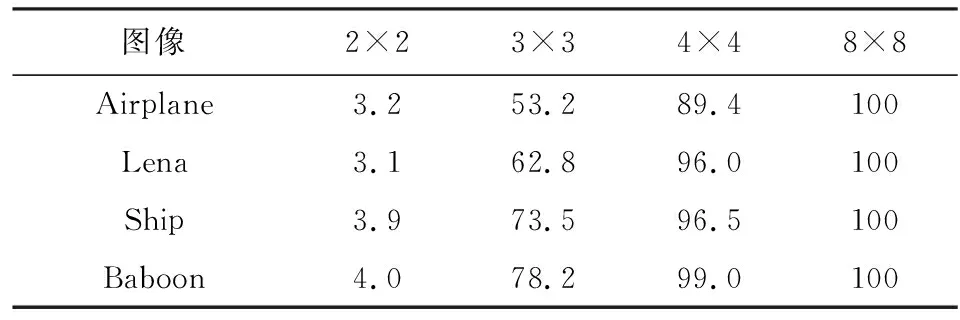
Table 2 Correct Rate of Block Scrambling Key for a Pair of Known-Plaintext Attacks

表2显示，随着图像分块的增加，块置乱密钥估计正确率增加，说明图像块个数与块置乱密钥成反比；当分块大小为3×3时，已经正确估计50%以上的块置乱密钥.分块增加到8×8时，块置乱密钥的估计正确率达到100%.而在相同分块下的不同图像，随着纹理图像复杂度的增加，等价集中σ增加，Ho增加，ρ′增加，这体现了NZBN特征的各异性.NZBN特征的各异性增加，块置乱密钥的估计正确率增加.与表1中块置乱密钥估计的理论正确率对比，实验得到的结果与理论值基本一致，说明块置乱密钥估计正确率与NZBN特征等价集总个数σ成正比，与图像块个数k成反比.

虽然恢复块置乱后的图像仍然是噪声图像，但不同分块下的噪声图像显露的轮廓不一样.随着分块大小的增加，噪声图像的轮廓越明显，恢复正确的图像块个数更多.如8×8下的噪声图像比4×4下的轮廓要清晰一些，比较表2中的块置乱密钥正确率也能得到相同的结论.

3.2.2 位平面置乱密钥的估计

在分块大小为8×8时，块置乱密钥正确率已经达到了100%，然而恢复块置乱后的图像仍然是1幅噪声图像，如图4(d)所示.这是因为Qin加密算法将明文图像高位平面的冗余转移到密文图像的低位平面，而没有冗余的低位平面被置换到了密文图像的高位平面.因此没有恢复位平面的图像仍然是1幅噪声图像，泄露图像信息的概率很小.进一步使用估计的位平面置乱密钥恢复位平面置乱，得到最终的恢复图像，如图5(d)所示.

Fig. 5 Result of a pair of known-plaintext attacks under different block sizes图5 不同分块大小下1对已知明文攻击的结果

以8×8分块下的Baboon图像作为已知明文攻击的测试图像，图6显示了3种图像的像素值分布情况，分别是明文Woman图像、仅恢复块置乱的Woman图像、最终恢复的Woman图像.仅恢复块置乱后的图像是1幅噪声图像，如图4(d)，且像素分布比较均匀，与明文图像的像素分布相差较大.而继续恢复位平面置乱后的图像能够显现图像轮廓，如图5(d)，且像素分布与明文图像的变化趋势相近，两者像素值比较接近.也就是说，位平面置乱转移了图像的冗余信息，使得没有恢复位平面置乱的图像与明文图像无关联，只有恢复位平面置乱，才能恢复部分冗余信息，使得恢复的像素值与明文像素更接近，从而引起图像的重要信息泄露.因此，仅恢复块置乱对于泄露原始图像信息是不够的，需要使用估计的位平面置乱密钥进一步恢复位平面置乱.使用不同分块大小下的不同图像估计位平面置乱密钥，恢复图像Z′得到最终的解密图像，如图5所示.

Fig. 6 Pixel distribution of plaintext image X and final restored image图6 明文图像X与最终恢复图像的像素分布

在8×8分块大小下，无论使用哪一对明-密文图像估计置乱密钥，最终估计的密钥都会泄露原始图像重要信息，如图5(d)所示.随着分块的减小，图像块NZBN特征的各异性减弱，更多的图像块具有相同的特征，给块置乱密钥的估计带来了困难，1对已知明文攻击的结果越来越模糊.当分块减小到3×3时，仍能泄露原始图像的部分信息，而继续减小到2×2分块时，解密图像是1幅噪声图像.由于2×2分块下的1对已知明文估计的块置乱密钥正确率不超过5%，没有正确恢复块置乱，就无法使用块内位平面的相关性估计位平面置乱密钥，因此最终的解密图像仍然是1幅噪声图像.也就是说，只有当块置乱密钥估计正确，才能进一步估计位平面置乱密钥.

位平面置乱密钥的正确率为

(21)

计算不同分块下不同图像的位平面置乱密钥正确率，如表3所示.

观察位平面置乱密钥正确率发现，即使块大小为8×8时，位平面置乱密钥正确率仍然不超过50%.使用估计正确率为100%的块置乱密钥解密Woman图像得到的图像仍然是噪声图像，如图4(d).而在位平面正确率不到50%的情况下，恢复位平面的图像竟然能显现原始图像的大部分信息，如图5(d)所示，这说明位平面置乱密钥具有弱密钥性.同时，也说明块置乱密钥才是关键.因为在较小分块下的块置乱密钥正确率不高，图像块恢复错误导致位平面置乱密钥无法被正确估计，最终恢复的图像仍存在大量的噪声点，尤其是2×2分块下的解密图像仍然是1幅噪声图像.为了解决这一问题，2.3节给出多对已知明文攻击方法，3.3节将给出实验证明2×2分块下仍然存在信息泄露的危险.

Table 3 Correct Rate of Bit-Plane Scrambling Key for a Pair of Known-Plaintext Attacks

3.3 已知明文对数对攻击结果的影响

3.2.2节给出了不同分块下1对已知明文攻击的攻击结果，1对4×4分块下的已知明文攻击已经基本能解密原始的所有信息.而2×2分块下的1对已知明文攻击无法破解加密密钥，使用估计的置乱密钥解密的图像仍然是1幅噪声图像.在增加已知明文对数后，2×2分块下是否能导致图像信息泄露呢？基于这一问题，对更小分块下明-密文图像进行多对已知明文攻击，选取明文图像中比较平滑的2对与3对图像分别进行测试，解密的Woman图像如图7所示.

Fig. 7 Attack results of multiple known-plaintext attacks under different blocks图7 不同分块下多对已知明文攻击的攻击结果

图7(a)显示，在2对明文图像均为平滑图像时，2×2分块下解密的Woman图像即使仍然存在噪声点，但已经泄露了图像信息.随着分块增加到3×3，解密图像的噪声点明显减少.也就是说，当明文图像仅为平滑图像时，较小分块下的加密图像也会引起信息泄露.增加已知明文对数到3对时，解密的Woman图像更为清晰，泄露了图像的更多信息，如图7(b)所示.使用多对已知明文攻击对置乱密钥取交集，能够得到更多τi=1的等价集，有效提高了块置乱密钥正确率，恢复的Woman图像更清晰.

图7表明，一旦增加已知明文攻击的对数，即使是2×2分块下的加密图像也无法抵抗本文提出的基于NZBN特征的已知明文攻击.

3.4 时间复杂度分析

时间复杂度是衡量一个算法攻击效果的重要指标之一.本文提出的1对已知明文攻击的算法时间的复杂度分析如下：

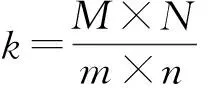
步骤2.位平面置乱密钥集合估计.对于k个图像块，查找密文图像块的8个位平面可能的置换位置，时间复杂度为O(8k).

因此，本文提出的已知明文攻击算法总时间复杂度约为8kmn+σ×τmax+8k=8MN+8k+σ×τmax，影响算法的时间复杂度主要因素是图像大小M×N与图像块个数k、等价集个数σ以及最大图像块个数τmax.在图像大小为512×512，测试不同分块下使用不同图像的1对已知明文攻击的运行时间，结果如表4所示.

表4显示，位平面置乱密钥的时间复杂度正如步骤2中描述的，与图像块总个数有关，随着分块大小的增加，图像块总数减少，位平面置乱密钥估计的时间减少.而对于块置乱密钥的估计，考虑到NZBN特征的各异性，不同图像不同分块下的NZBN特征分布不同，使得块置乱密钥估计具有时间差异.但整体上而言，随着分块大小的增加，图像块总个数减少，等价集个数σ减少，同时等价集中最大图像块个数τmax减少，因此块置乱密钥估计的时间减少.

Table 4 Actual Running Time of a Pair of Known-Plaintext Attacks Under Different Blocks for Different Scrambling Keys

4 结 论

Qin提出的冗余转移加密算法，在一定程度上提高了加密算法的安全性.本文定义了图像块的NZBN特征，分析指出了该特征在Qin算法加密前、后具有恒定不变的特点.在此基础上，提出了一种基于NZBN特征的已知明文攻击方法，并给出了多对已知明文条件下如何进一步提高密钥估计正确率的攻击方法.该攻击方法先估计块置乱密钥，再估计每个图像块的位平面置乱密钥，打破了现有已知明文攻击的实施条件——加密前后像素值不变.最后分析讨论了不同分块大小下的算法性能和时间复杂度。实验结果表明，在分块大小为4×4的条件下，仅用1对明-密文图像，即可恢复89%以上的块置乱密钥，从而导致原始图像信息泄露.

作者贡献声明：罗雅婷负责方案论证、实验数据处理与分析，以及论文撰写；和红杰指导研究方案、论文结构与实验设计、论文修改；陈帆提出论文选题，指导研究方案和论文修改；屈凌峰指导实验设计和论文修改.