FPCBC: 基于众包聚合的联邦学习隐私保护分类系统

金 歌 魏晓超 魏森茂 王 皓

(山东师范大学信息科学与工程学院 济南 250358)

机器学习在模式识别、医疗等领域扮演了重要的角色，通过机器学习实现分类的需求也逐渐出现在各个应用领域.传统机器学习解决方案的思想是训练出理想的模型，再进行分类推理.然而，由于硬件和有限本地训练数据的限制，导致本地训练出来的模型表现不佳.普遍的想法是从多个数据持有方收集数据来训练模型，但是在很多情况下数据都很敏感[1].与此同时，相关法律法规[2-3]的出台，禁止了在没有明确协议的情况下收集和利用私人敏感数据的行为，导致数据是离散且不共享的.如今为了使机器学习应用在适应社会实际需求的同时保证隐私安全，引入云的机器学习(cloudera machine learning, CML)成为了热点，其中联邦学习(federated learning, FL)应运而生.

当前有很多方法可以实现数据分类，其中实用的解决思路分为2类：

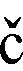
第2类，不再以联合训练出理想模型为目的，而是让边缘机构(持有训练数据的参与方)本地训练出准确度不高的弱模型，然后对弱模型推理出的弱结果进行满足统计学的迭代聚合处理来得到理想的分类结果.Zhang等人[11]基于这种解决思路进行了研究并提出了一种可行的算法.

上述方案分别在实用或安全上存在局限性.首先，第1类方案虽然在一定程度上保护了训练数据的隐私，但存在很多问题亟待解决，如：非独立同分布的数据集极大地降低了联邦学习的整体性能[12]，且需要占用边缘设备大量的通信带宽.共享梯度信息也会引起攻击者的注意，一些研究[4,13]提出了基于联邦学习方法中共享模型参数的攻击，虽然后续对梯度隐私安全有所研究，但仍需要多个数据提供方和云服务器之间进行大量冗杂的通信来训练出理想的模型.其次，第2类需要用户或者查询方分享分类的数据，这些数据在公共线路传输的过程中极易受到外部敌手拦截、窃取，从而导致数据泄露产生隐私安全问题.与此同时，边缘机构也会直接获得查询数据从而可能对用户的查询私密数据加以利用，此类系统内部敌手也会严重威胁用户的隐私安全.

考虑到机器学习即服务(machine learning as a service, MLAAS)最终目的是服务于社会市场，边缘参与方的独立性又具有较强的需求.因此，为了实现分类而要求各个边缘机构长时间保持通信来联合训练模型是比较奢侈的方法.为了解决这个缺陷的同时提供更好的隐私安全保障，我们基于上述第2类思想提出了一个安全众包聚合的联邦学习隐私保护分类系统(federated learning privacy-preserving classification system based on crowdsourcing agg-regation, FPCBC).我们并不直接将需要分类查询的数据上传给服务器，而是通过密码学技术对数据加密，边缘机构使用弱模型对加密的数据进行推理，进而得到密态分类结果，再由服务器对密文结果进行聚合迭代处理得到最终分类结果.虽然系统解决机器学习问题的方式不再是通过传统联邦学习来联合训练模型，但FPCBC仍秉承了联邦学习“分邦而治”的思想，实现了机器学习应用的联邦场景，且着力解决了隐私问题.此外，FPCBC更适合社会的应用环境，边缘机构之间无需过多的依赖关系与通信，将大部分的计算工作交给云服务器，缓和了当前物联网和边缘应用产生的负担.

本文的主要贡献总结为3个方面：

1) 将众包、联邦学习思想与密码学技术相结合，在利用统计聚合法实现分类的过程中通过密码学技术加密数据，防止边缘机构和服务器获得私密数据，从而达到保护查询数据隐私安全的目的.我们解决了边缘机构合谋窃取用户查询数据的问题，并阻断了外部敌手窃取用户隐私的可能性.

2) 与现有的实现分类目的的模型相比，我们基于双服务器提出的FPCBC能保护用户的数据不泄露给外部敌手的同时对边缘机构的丢失也具有更强的鲁棒性.由于外包的特性，用户的本地计算量较少;此外，与传统联邦学习分类的解决方案相比，实现分类的过程不需要训练出理想的模型，边缘机构在系统中的存在更加独立，因此，所提出的方案可以满足许多实际应用中的真实需求.

3) 实验结果表明，我们提出的模型是可行的，在无需训练理想模型且保证一定准确率的前提下从本质上提高了模型的安全性.

1 相关工作

1.1 安全模型训练

传统隐私保护机器学习的重点在于安全模型训练，目前经常使用外包或协同训练的方法，其中协同训练通常使用联邦学习.目前对于联邦学习的研究，除了把重点放在寻找高效的模型以外，如何在训练过程中保障数据提供方的隐私安全也成了交叉领域的研究方向.对于这种传统隐私保护联邦学习的研究，Phong等人[14]提出了一个隐私保护的深度学习系统，该系统桥接了深度学习和密码学，将异步随机梯度下降应用于神经网络，并结合加法同态加密(homomorphic encryption, HE)增加了可容忍的开销.Bonawitz等人[15]设计了一种新颖、通信高效的协议，用于高维数据的安全聚合，他们提出的协议允许服务器以安全的方式计算大型用户所持有的数据向量的总和，且该协议的通信开销很低.对于16位输入值，协议为2个用户和二维向量提供1.73倍的通信扩展，以及在明文中发送数据的1.98倍扩展.Dong等人[16]基于三元梯度压缩的技术研究提出了更加安全和高效的联邦学习系统，他们首先分析了三元梯度压缩的隐私泄露问题，设计了攻击策略并发起攻击，分别设计了基于Shamir的门限秘密共享(threshold secret sharing, TSS)和Paillier同态加密的隐私保护协议，实现了利用三元梯度压缩技术的联邦学习系统.Fang等人[17]提出了一个隐私保护和通信高效的物联网联邦学习方案，该方案通过梯度空间稀疏化来防止偏离收敛趋势的无关局部更新被上传利用，使用压缩算子来实现双向压缩并提出了秘密共享与轻量级同态加密相结合来保护数据隐私、抵御各种共谋场景的隐私保护协议.

这些机器学习训练过程的隐私保护方案虽然相对成熟，结合了同态加密、秘密分享等密码学技术保护了模型训练过程中的梯度等隐私，但是需要多个数据提供方和云服务器间维持大量冗杂的通信来训练模型，这些因素在实际应用于市场时存在一定的约束.我们的方案尽可能从另一种角度和思路上实现隐私保护.

1.2 安全模型推理

MLAAS往往通过模型推理的方法来实现应用目的，如图1所示，用户持有数据Data，服务器有已经训练好的神经网络模型Model.服务器基于模型Model对Data输出一个预测Result=P(Data，Model).安全模型推理就是训练出模型之后，用户对数据加密后再进行推理，这样是为了解决用户直接将数据上传而产生的安全问题.安全模型推理往往基于交互的方式或非交互的方式来实现.

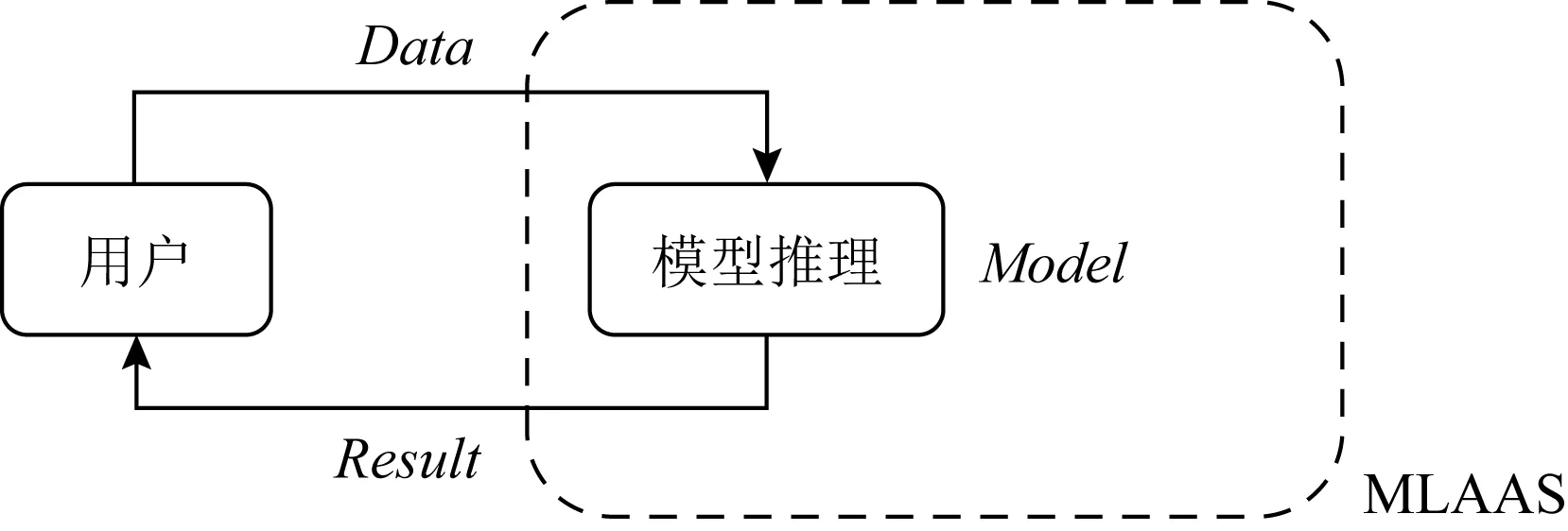
Fig. 1 Description of MLAAS application relationship图1 MLAAS应用关系说明

交互方式在推理过程中需要用户在线参与并执行必要的交互计算，MiniONN[18]使用加法秘密共享的安全两方计算技术，其中用户和服务器各拥有一份秘密份额在线协同计算，通过将现有神经网络转换为茫然神经网络来实现安全推理.GAZELLE[19]和BAYHENN[20]使用同态加密，并分别使用混淆电路和对DNN结合贝叶斯网技术实现了高效的推理任务.除此之外，更多满足离线推理的非交互式方案也得到了研究[21-25]，这些非交互式允许用户处于离线状态，仅需用户执行数据预处理和上传，然后等待返回推理结果即可.CryptoNets[22]是于2016年提出的神经网络模型，使用了Bos等人[26]于2013年提出的一种分级同态加密方案，并对池化层、卷积层等做了能够满足同态加密操作的变换(详见2.3节)，本文选择了基于CryptoNets的实验进行了分析.CryptoDL[23]使用全同态加密，将非线性函数通过对多项式进行拟合，使得同态加密处理非线性函数成为实际，进而构建出满足同态加密计算的神经网络模型.Faster CryptoNets[24]也使用全同态加密，并使用网络剪枝来实现模型.Ahmad等人[25]遵循了CryptoNets[22]中提出的框架，并应用他们的GPU加速FHE技术，首次实现了高效的、利用GPU计算的同态卷积神经网络(HCNN).

本文提出的安全分类系统借助安全模型推理的思想，摆脱了安全模型训练的过程和对训练理想模型的需求，将密码学与众包聚合方法[11]结合，从而实现隐私安全的分类应用.

2 基础知识

2.1 同态加密

同态加密(HE)是一种特殊的密码学加密手段，Rivest等人[27]在1978年提出了同态加密的概念，直到2009年，Gentry[28]才从数学上提出了基于理想格的全同态加密方案，之后对同态加密方案也有了新的研究进展[29-31].同态加密允许对密文直接进行特定的代数运算，得到的密态运算结果解密后与对明文进行操作的结果一样.例如，给定2个密文[x1],[x2],[x1]=Enc(pk,x1), [x2]=Enc(pk,x2)，若密文操作⊙满足Enc(pk,x1+x2)←[x1]⊙[x2]和Enc(pk,x1×x2)←[x1]⊙[x2],则加密方案满足同态加法和乘法操作.同态加密安全性要求基础加密方案满足CPA安全.

同态加密方案H通常由四元组组成：H={KeyGen,Enc,Dec,Eval}.其中，KeyGen是密钥生成函数，用于生成加密方案需要的密钥;Enc是加密函数，对于非对称同态加密，该函数将一个公钥pk和明文m作为输入，并产生一个密文c=Enc(pk,m);Dec是解密函数，对于非对称同态加密，该函数将一个私钥sk和密文c作为输入，生成明文m=Dec(sk,c);Eval是评估函数，将一个公钥pk、c和对明文的正确操作T作为输入，输出与明文对应的密文，用于验证加密算法的正确性.方案H在满足下列式子时是正确的：

c′←Eval(pk,c,T)⟹T(m)=Dec(sk,c′).

本文在利用同态加密实现外包分类的过程中，输入神经网络的数据C往往是与特征有关的数据：明文数据m=(x1,x2,…,xn)和密文数据C=([x1],[x2],…,[xn])，其中xi是明文，[xi]是经过同态加密的密文,i∈{1,2,…,n}.然后将密文交给神经网络进行学习，系统流程如图2所示:

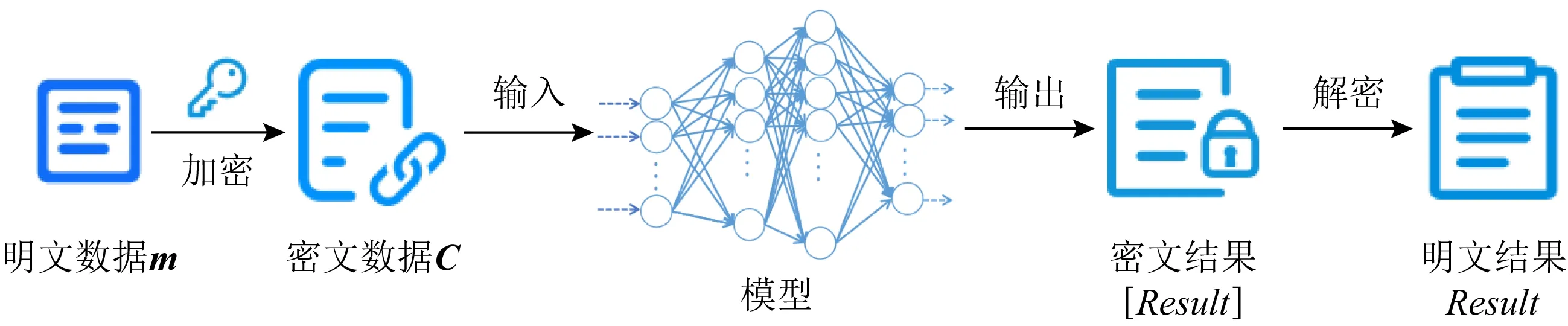
Fig. 2 Process of homomorphic encryption outsourcing classification图2 同态加密外包分类流程

由于满足同态推理的神经网络往往需要与之对应合适的加密方案，因此在安全模型推理中不同的机器学习模型采用的加密方案并不唯一.我们提出的系统要求加密方案满足加法和乘法同态即可适用，因此在介绍总体方案时将以功能模块的形式进行描述，且密文操作省略模运算的描述说明.此外，一些加密方案不支持浮点数运算，我们往往通过适当的缩放将它们转换为整数，当然也有其他的解决方法[32].

实验部分使用满足同态加密推理的CryptoNets模型，并使用Bos等人[26]提出的YASHE分层同态加密(leveled homomorphic encryption, LHE)的加密方案.

2.2 联邦学习

联邦学习是谷歌于2016年提出的能够保护数据隐私的一种分布式机器学习框架，目前研究[33]对于联邦学习有了更包容的定义:联邦学习是一种机器学习范式，它指在中央服务器或服务提供商协调下，多个实体(客户端)协同解决机器学习问题.联邦学习分为3个类别:横向联邦学习(horizontal federated learning, HFL)、纵向联邦学习(vertical federated learning, VFL)和联邦迁移学习(federated transfer learning, FTL).其中，HFL的特点是训练数据的来源交叉度低，但是数据属性交叉度很高，这种数据分布多出现于同一性质的企业或机构采用相同的数据库属性划分系统，例如医院等.

在分布式系统中，为了实现分类任务，虽然联合训练模型的边缘参与方所拥有的数据大都是非独立同分布的，但训练数据的属性通常是相同的.因此，我们在隐私保护分类系统中要解决的问题类似于HFL的应用场景.受联邦学习的启发，我们将密码学技术融入其中设计出更安全的分类系统.

2.3 CryptoNets神经网络

CryptoNets是Dowlin团队提出的一个神经网络模型，该模型使用多项式近似的方式来代替ReLU激活函数，实现了在加密数据上运行神经网络的可能性，其加密方式使用Bos等人[26]提出的分层加密方案进行加密，并允许进行加法和乘法运算.Crypto-Nets的训练和推理采用不同的方式：训练过程基于明文采用更复杂的网络层，推理过程则使用简化的网络结构，可以实现基于密文的推理.因此，在推理阶段，这种方式在外包计算时可以保证数据的私密性，能为机器学习的预测即服务(prediction as a service, PAAS)思想提供隐私保障.

为了节省推理时间，CryptoNets合并了连续的线性变换层.整个神经网络的搭建分为2部分：训练网络和简化网络，后者仅用于预测.训练网络有9层，简化网络有5层，如表1所示:

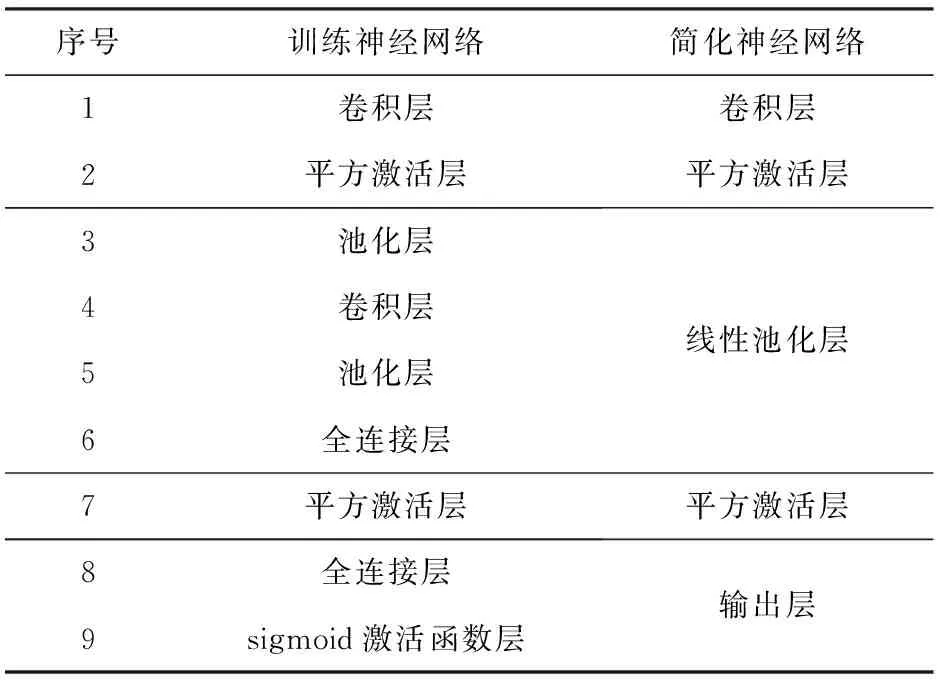
Table 1 Neural Network Layers of CryptoNets

本文的实验以CryptoNets为例，对MNIST数据集进行实验测试.当然，我们可以用黑盒的方式获取模型的推理结果，对于任何满足加乘同态推理的神经网络，我们提出的系统方案都有一定的普适性.

2.4 Spearman秩相关系数

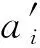
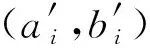
2.5 SC-AGG算法

SC-AGG[11]是一种结合联邦学习的轻量级迭代聚合算法，在边缘参与方使用本地有限数据训练出准确度不高的模型后，该算法根据网络模型推理出的结果Wr(该分类推理结果的准确度较低，本文之后称之为弱结果)由中心代理再进行迭代聚合处理，从而得到准确率较高的分类结果Result(本文之后关于此类推理结果简称强结果)，使用该算法的应用架构如图3所示:

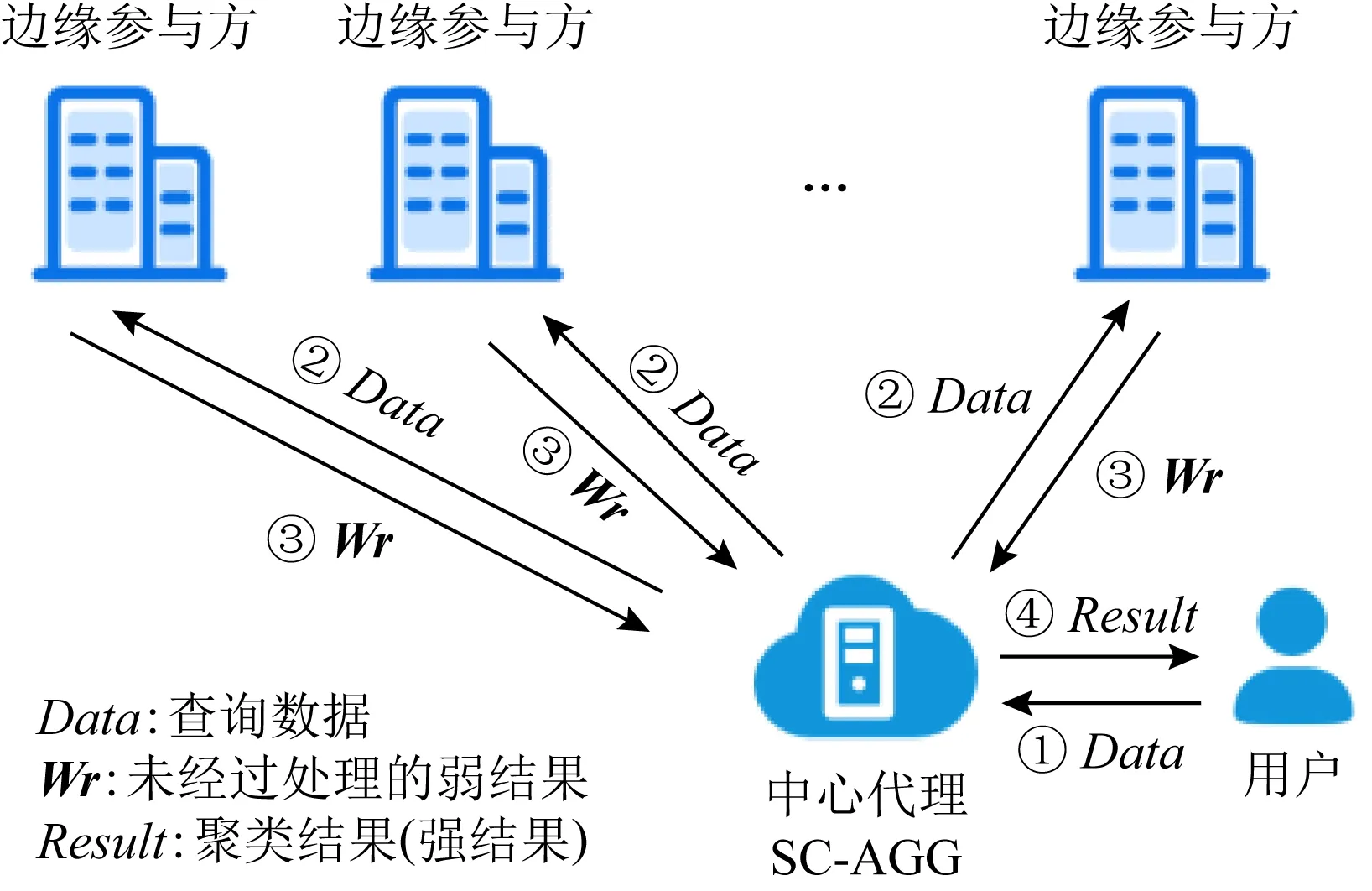
Fig. 3 Federated learning aggregation system architecture using SC-AGG图3 使用SC-AGG的联邦学习聚合系统架构

算法SC-AGG基于统计学的思想，对多方推理的弱结果进行符合统计意义的处理，进而生成高准确度的结果.假设使用该算法对一组数据Data进行分类，执行Ω轮可以得到理想结果，那么执行到第τ轮时，τ∈{1,2,…,Ω}，需要计算Estiτ，Wτ和Foreτ这3个关键量.对于该组数据Data的任一个查询数据而言：

Estiτ={(L1,L2,…,Ln)}是对单条查询数据分类分布的预估计值，其中Li表示估计数据划分为第i类的概率大小,i∈{1,2,…,n}.Estiτ计算依赖2个超参数α和ρ，其中α∈(0,1)用来判断可信度最小阈值，ρ∈(0,1)是一个概率衰减参数，用于将估计的概率分布替换为加权1的概率.如果max(Estiτ -1)<α，那么执行计算Estiτ的中心服务器判定本轮Estiτ不可信，则Estiτ以1-ρτ的概率被赋值为Foreτ -1，以ρτ的概率被赋值为Estiτ -1，否则Estiτ直接被赋值为Estiτ -1.

Wτ=(E1,E2,…,En)是为了强化边缘参与方模型的优势，弱化模型的不足而设计的反映模型能力的权重矩阵.对于每个弱模型能力而言，越高的Ei则表示模型在τ轮迭代后对类别i的区分能力越强.Wτ的计算依赖于前一轮的能力矩阵Wτ -1和查询数据分布之间的相关性来计算，由于能力矩阵和查询数据都不是独立同分布的，所以两者之间选择2.4节介绍的Spearman秩相关系数来计算相关性：

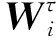
Foreτ={(F1,F2,…,Fn)}是对单条查询数据第τ轮的最终聚合结果，也是整个算法最关键的输出，其中元素Fi表示分类划分判定为第i类的概率大小,i∈{1,2,…,n}.Foreτ的计算受到能力矩阵W、接收到来自边缘参与方的弱结果Wr和自身Foreτ的影响:

本文的系统实现使用简化的SC-AGG算法，使其能够融合密码学技术大幅度提高隐私安全性的同时，保证最终结果拥有可观的准确性，具体算法详见4.2.1节.

2.6 softmax函数

softmax函数的作用是归一化，目的是将多分类的结果以概率的形式展现出来.该函数将多个神经元的输出映射到(0,1)区间内从而看成概率，进而实现多分类，基本流程如图4所示:

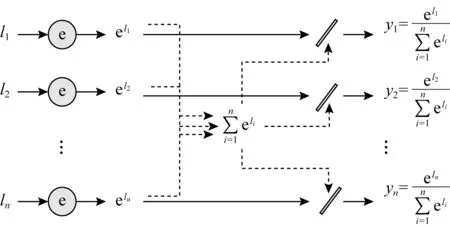
Fig. 4 Calculation flow chart of softmax图4 softmax计算流程图

根据输入X=(l1,l2,…,ln)，得到预测出的结果Y=(y1,y2,…,yn)的关系满足：

预测函数P(yi|X)分解为2个步骤：

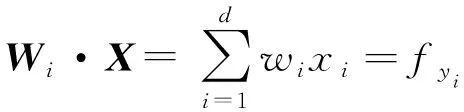
2) 使用softmax函数得到归一化概率

3 系统模型及安全定义

本节首先描述FPCBC分类系统构造，再对本文要解决的问题进行形式化描述，最后指出本文的安全定义.

3.1 系统模型

系统模型中有3类角色：边缘参与方(训练弱模型的数据持有方)、双服务器(计算的主要承担方)和用户(系统的受益方，提供需要分类的数据).我们的系统目标就是将分类任务众包给边缘参与方和服务器进行分类，其分类过程需要的大量计算交给拥有高计算能力的服务器执行.用户只与中心服务器进行通信，从而隔断了用户与边缘参与方的通信，中心服务器负责将用户提供的数据发送给边缘参与方并收集弱分类结果，然后利用双服务器进行满足统计学的安全迭代聚合操作，最终得出最优分类结果.图5显示了我们提出系统模型的总体架构.

1) 边缘参与方.边缘参与方持有机器学习的训练数据Datai，并基于本地敏感的私有数据训练出一个弱模型，该模型并不复杂且拥有对密文进行推理的能力.本文中各个边缘参与方相对独立，为了保障隐私安全，不再互相共享训练数据和模型参数.除此之外，由于他们的私有数据是多样且不可预测的，因此各个参与方训练出弱模型的推理性能也有不同.

2) 用户.用户持有待分类的不带标签的数据集Dinq，用户将Dinq进行加密并发送给服务器A.整个系统通过众包的形式实现分类查询，因此用户不与任何边缘参与方进行通信，服务器是用户在系统中通信的唯一接口.

3) 服务器.服务器是用户与边缘参与方之间的中介，我们提出的整个系统中存在2个服务器.服务器A负责收集来自边缘参与方的弱结果，并通过与服务器B的交互来安全迭代聚合弱结果，从而得到最终的预测结果.2个服务器承担了系统的主要计算量，从而削弱边缘参与方和用户的负担，这对实际应用是十分友好的.为了实现弱到强结果的聚合，服务器A拥有一个小型公开的带有标签的数据集Dlab，该数据集可以由边缘机构提供或公开收集，且该数据集的分布特征不会揭示系统中其他数据集的分布情况.

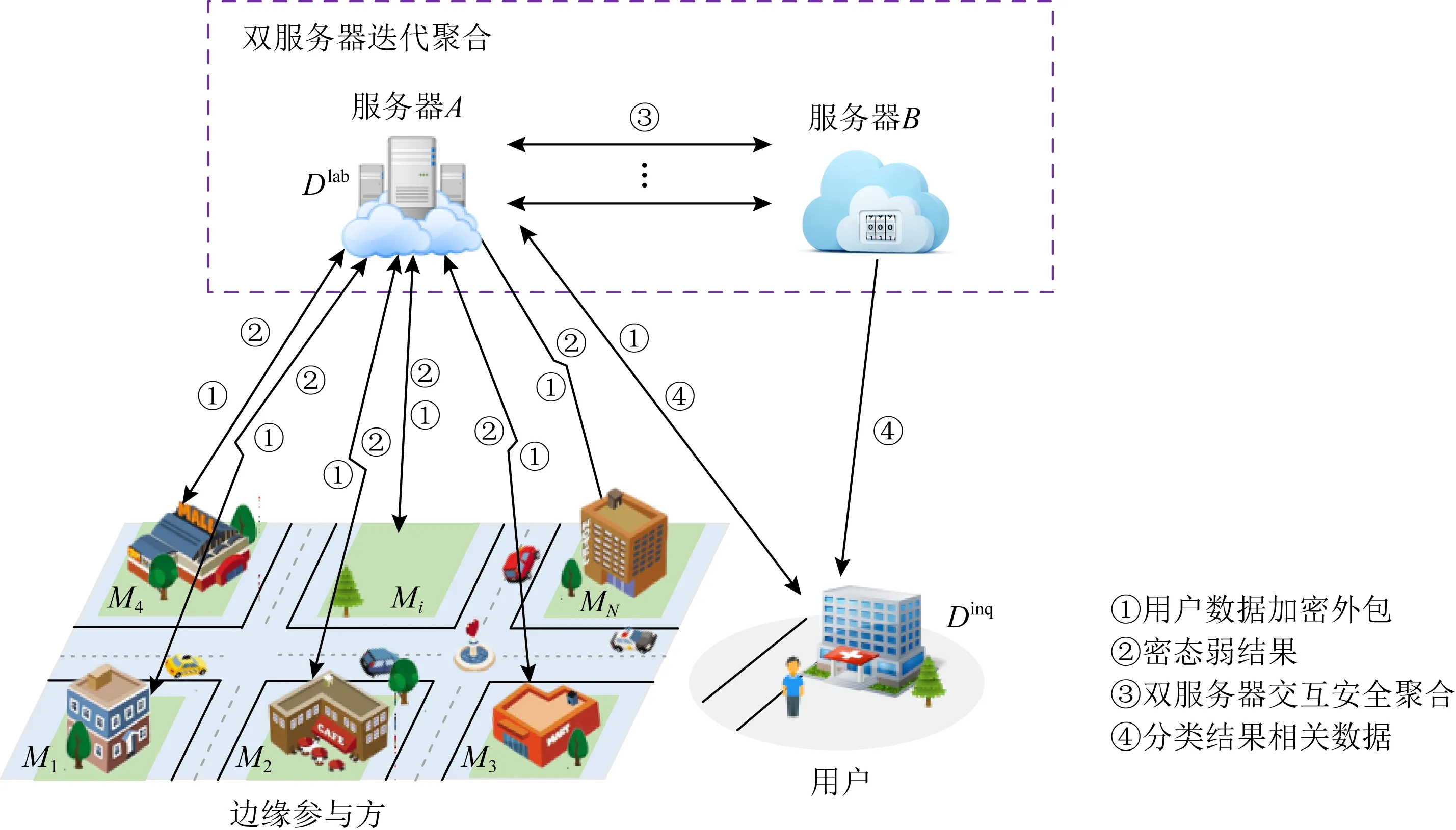
Fig. 5 Privacy-preserving classification system based on crowdsourcing aggregation图5 众包聚合的隐私保护分类系统

系统的关键数据流如图5中的①～④，更详细的实现见4.2.2节.①表示用户将数据加密外包给边缘参与方的过程，②表示边缘参与方将密态的弱结果发送给服务器A，①②为双服务器聚合出更高准确率的结果做准备，③表示双服务器通过交互来实现安全聚合.聚合完成后，④表示双服务器将与分类结果相关的数据发送给用户，最后用户本地计算恢复出最终的分类结果.

3.2 问题形式化

本节形式化描述FPCBC所解决的分类问题，表2对常用的变量和超参数进行了描述.

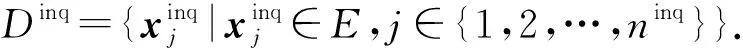
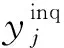
为了更严谨地表述，本文基于假设：任何边缘参与方和服务器都不能基于本地所有的数据集Datai和Dlab来提前预测出Dinq的标签概率分布，且对于任何能够对Dinq进行分类的非线性函数F满足:

Pr(F(Dlab,{Data1,Data2,…,DataN})=ξ)=ε,

其中ε是可忽略的.

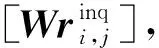
Result=arg max(ForeΩ).

我们的目标是在不泄露隐私的前提下让用户得到更高准确度的查询分类结果，可以用下面的公式形式化地衡量我们的标准:

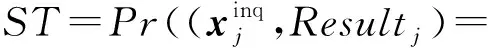
我们系统的最终目标是提升ST，ST越大说明准确率越高.

Table 2 Systematic Variables and Hyperparameters

3.3 安全模型

我们的系统方案在半诚实和服务器不合谋的前提下是安全的.首先，半诚实意味着边缘参与方和服务器在训练模型和执行方案期间遵守规定，但是对来自外部的数据信息保持好奇，尝试去获取私有数据并分析数据;其次，双服务器之间是不合谋的，也就是说服务器不会串通来获取用户的私有信息.需要注意的是，系统在一定程度上也可以防止外部敌手窃取用户的查询数据Dinq.在本文中不考虑那些通过发送干扰计算结果或者修改数据集来干扰正常聚合计算的恶意参与方和服务器.

在我们的方案中，第1个关键的隐私要求是用户的数据隐私和分类结果隐私，这意味着用户的数据在众包系统分类的过程中不会泄露，而且参与众包的各方(边缘参与方和服务器)能够在不知分类结果的前提下，让用户获得最终分类结果.另一个隐私是系统中进行机器学习训练的数据集隐私.接下来，我们基于以下实验给出分类结果隐私的形式化定义:

(pk,sk)←Initialization(1k)

查询1：

① forl=poly(k)

② 敌手Foeselecti∈{1,2,…,ninq},j∈{1,2,…,nlab} and query for:

③Foe←Dlab′,Foe←NetInfer(Dj),Dj∈Dlab′;

④ [Di]←Enc(pk,Di),Di∈Dinq;

⑤Foe←NetInfer([Di]).

查询2：

① forl=poly(k)

②Foeselecti∈{1,2,…,ninq} and query for:

③ [Di]←Enc(pk,Di),Foe←[Di],Di∈Dinq;

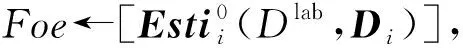
Foe←NetInfer([Di]);

⑤Foe←InteractionA(*).

查询3：

① forl=poly(k)

②Foeselecti∈{1,2,…,ninq},Di∈Dinqand

query for:

③Foe←(pk,sk);

④Foe←InteractionB(*).

挑战：

①Foeselecti∈{1,2,…,ninq},Di∈Dinq;

②L0←NetInfer(Di);

③L1←NetInfer(R);

④b←{0,1},Foe←Lb;

⑤b′←Foe;

⑥ ifb′=boutput 1; else output 0.

定义1.分类结果隐私. FPCBC是分类结果隐私安全的，如果对于任何概率多项式时间(probabi-listic polynomial time, PPT)敌手Foe：

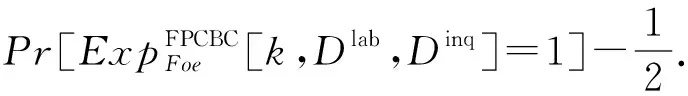
实验分为2个阶段：查询和挑战.实验中，k表示安全系数.NetInfer(*)表示边缘参与方根据弱模型对数据推理出的分类结果;为了简化实验表述，InteractionA(*)表示双服务器交互期间服务器A能获取到的数据，同理InteractionB(*)表示双服务器交互期间服务器B能获取到的数据.查询阶段分为3种来分别模拟系统中的边缘参与方、服务器A和服务器B的真实情况.每次实验允许敌手多项式次执行一种查询并执行挑战来模拟FPCBC中某一方.挑战阶段，随机选取一个用户查询数据Di，R是一个大小等特征都与Di一致的随机矩阵.若敌手Foe不能以不可忽略的概率区分模型对Di和R的分类结果，那么FPCBC满足分类结果隐私安全.

4 FPCBC总体方案

我们的方案需要在不泄露隐私的前提下，通过双服务器交互来实现聚合算法的密态计算，从而实现隐私保护分类查询.本节首先介绍我们提出的交互算法，再根据简化的SC-AGG算法[11]给出完整的FPCBC方案，并对方案的总体实现进行描述.

4.1 双服务器交互算法

4.1.1 安全计算softmax算法：SCsoftmax

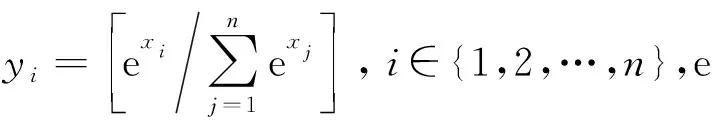
服务器A持有[X]和公钥pk，服务器B持有密钥对(pk,sk)，每次执行SCsoftmax算法时：

1) 服务器A生成一个与xi，i∈{1,2,…,n}等长的随机数r1，并生成与X等长的向量R1=(r1,r1,…,r1)，将其加密Enc(R1,pk)=[R1]=([r1],[r1],…,[r1])，然后根据同态加计算：

[X]⊙[R1]=[X+R1],

将其发送给服务器B.

2) 服务器B解密Dec([X+R1],sk)=X+R1=(x1+r1,x2+r1,…,xn+r1)，再做指数运算并加密：

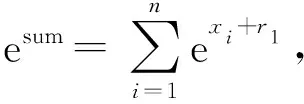
将加密结果发送给服务器A.

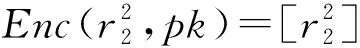
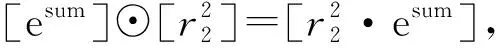
将加密结果发送给服务器B.

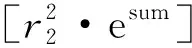
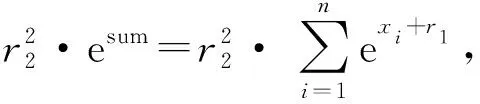
因此，服务器B可以计算求得

并将其加密Enc(Q,pk)=[Q]后发送给服务器A，Q的推导过程为

其中，q∈{1,2,…,n}.

5) 服务器A计算：

[Q]⊙[R2]=[Q·R2]=

[softmax(X)].

算法1.SCsoftmax([X],pk,sk).

输入：密文[X]=([x1],[x2],…,[xn])、公私钥(pk,sk)；

输出：[softmax(X)].

服务器A：

① 生成随机向量并加密：

R1=(r1,r1,…,r1)，其中r1是随机数

|r1|=|[xi]|,i∈{1,2,…,n}, [R1]←Enc(R1,pk);

② 计算[X]⊙[R1]=[X+R1]并发送给服务器B;

服务器B：

③ 使用sk解密[X+R1];

④ 计算eX+R1,esum;

⑤ 加密步骤④计算结果,并发送给服务器A;

服务器A：

⑥ 生成随机向量：

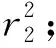
⑦ 计算[eX+R1]⊙[R2]=[R2·eX+R1],

并发送给服务器B;

服务器B：

⑧ 对接收到的经过步骤⑦计算得到的数据解密后计算Q;

⑨ 加密为[Q]并发送给服务器A;

服务器A:

⑩ 计算返回值[softmax(X)].

4.1.2 安全密态计算max算法：SCmax

对于一个明文X=(x1,x2,…,xn)经过同态加密之后的密文[X]=([x1],[x2],…,[xn])←Enc(X,pk).使用SCmax可以实现安全求出X中的最大值与某阈值v之间的大小关系.我们提出的该算法可以不泄露明X，算法2总结了该算法通过双服务器交互实现的流程.

算法2.SCmax([X],pk,sk,v).

输入：密文[X]=([x1],[x2],…,[xn])、公私钥(pk,sk)、阈值v；

输出：boolean.

服务器A：

① 生成随机向量并加密：

R3=(r3,r3,…,r3)，其中r3是随机数

|r3|=|[xi]|,i∈{1,2,…,n}；

Enc(R3,pk)→[R3]=([r3],[r3],…,[r3]);

② 计算[X]⊙[R3]=[X+R3],

[S]shuffle([X+R3]),

并将[S]发送给服务器B;

服务器B：

③ 使用sk解密[S];

④ 计算cpmax(S)-v，并发送给服务器A;

服务器A：

⑤ 计算fcp-r3;

⑥ iff>0 then

⑦ returnboolean=false;

⑧ else

⑨ returnboolean=true.

服务器A持有[X]和公钥pk，服务器B持有密钥对(pk,sk)，每次执行SCmax算法时：

1) 服务器A生成与xi，i∈{1,2,…,n}等长的随机数r3，并生成与X等长的向量R3=(r3,r3,…,r3)，将其加密Enc(R3,pk)=[R3]=([r3],[r3],…,[r3])，然后根据同态加计算：

[X]⊙[R3]=[X+R3],
[S]shuffle([X+R3]),

其中shuffle(*)是打乱向量内部项顺序的功能函数，将打乱后的向量[S]发送给服务器B.

2) 服务器B解密[S]得S，计算cpmax(S)-v并发送给服务器A.

3) 服务器A计算fcp-r3，如果f>0，则服务器A判定[X]中的最大值不小于阈值v，否则小于v.

4.1.3 安全密态计算Spearman算法：SCspear

对于一个明文X=(x1,x2,…,xn)和一个经过同态加密之后生成的密文:[Y]=([y1],[y2],…,[yn])←Enc(Y,pk).我们提出的算法可以在不泄露明文向量Y的前提下，安全计算出X和Y之间的Spearman秩相关系数.算法3总结了该算法通过双服务器交互实现的流程.

算法3.SCspear([X],[Y],pk,sk).

输入：明文X=(x1,x2,…,xn)、密文[Y]=([y1],[y2],…, [yn])、公私钥(pk,sk);

输出：Cor.

服务器A：

① 生成随机向量并加密：

R4=(r4,r4,…,r4)，其中r4是随机数

|r4|=|[xi]|,i∈{1,2,…,n},

Enc(X,pk)→[X],

Enc(R4,pk)→[R4]=([r4],[r4],…,[r4]);

② 计算[X]⊙[R4]=[X+R4],

(Γ,[Ψ])shuffle(X,[Y+R4]),

并将(Γ,[Ψ])发送给服务器B;

服务器B：

③ 使用sk解密[Ψ];

④ 计算Φ=sort(X,Ψ),

Cor=Spearman(Φ);

⑤ 最后将Cor发送给服务器A;

服务器A：

⑥ 返回值max(0,Cor).

服务器A持有X,[Y]和公钥pk，服务器B持有密钥对(pk,sk)，每次执行SCspear算法时：

1) 服务器A生成一个与yi，i∈{1,2,…,n}等长的随机数r4，并生成与[Y]等长的向量R4=(r4,r4,…,r4)，将其加密Enc(R4,pk)=[R4]=([r4],[r4],…,[r4])，然后根据同态加计算：

[Y]⊙R4=[Y+R4],
(Γ,[Ψ])shuffle(X,[Y+R4]),

其中shuffle(*,*)表示对内部2个向量按照相同的方式打乱项的顺序，Γ,[Ψ]分别是X和[Y+R4]打乱后的结果，然后将向量对(Γ,[Ψ])发送给服务器B.

2) 服务器B解密Dec([Ψ],sk)=Ψ(Ψ是经过打乱顺序的Y+R4)，然后计算：

Φ=sort(X,Ψ),

其中sort(*,*)表示对内部2个向量按照升序(或降序)排列，并生成2个向量相应的秩次序列对Φ，最后根据Spearman计算规则(详见2.4和文献[34])求出相关系数值：

Cor=Spearman(Φ).

4.2 总体方案

4.2.1 SSC-AGG算法

本文的系统实现使用简化的SC-AGG算法，该算法使系统能够在融合密码学技术大幅度提高隐私安全性的同时，保证最终结果拥有可观的准确性.为了使该算法能够适用于我们提出的安全需求，我们将Zhang等人[11]提出的该聚合算法稍作简化转变为SSC-AGG算法.经过转变的SSC-AGG算法不会损失过多精度，而且能够实现我们的安全需求.算法4对初始化和迭代计算2个部分进行了描述，应用于系统实现的过程见4.2.2节.

算法4.SSC-AGG.

初始化

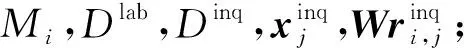
输出：Esti0，W0，Fore0.

① forj=1,2,…,ninqdo

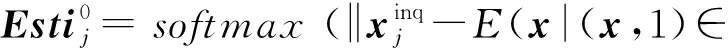
Dlab)‖2);

③ end for

④ fori=1,2,…,Ndo

⑤ forl=1,2,…,Ldo

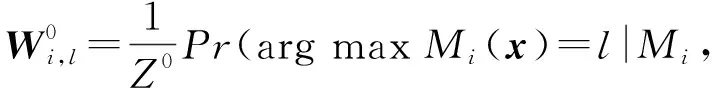
(x,l)∈Dlab);

⑦ end for

⑧ end for

⑨ forj=1,2,…,ninqdo

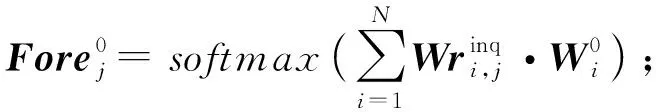
迭代

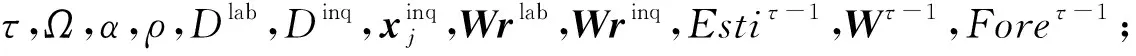
输出：Estiτ，Wτ，Foreτ.

① forτ=1,2,…,Ωdo

② forj=1,2,…,ninqdo

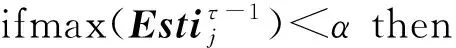
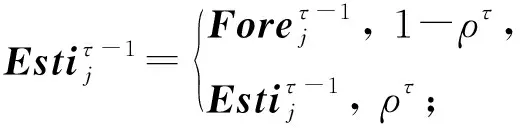
⑤ end if

⑥ end for

⑦Estiτ←Estiτ -1;

⑧ fori=1,2,…,Ndo

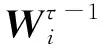
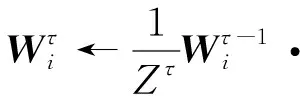
⑨ end for

4.2.2 FPCBC系统

虽然使用算法4能够实现弱到强结果的聚合，但是计算过程需要传递的信息会完全暴露在系统之中.为了防止隐私泄露，我们提出了FPCBC，用户能够获取想要的结果，且任何隐私数据都不会暴露给系统内的其他参与者.表3对我们方案进行了简单概述，我们的协议分为4个阶段：

1) 预准备阶段.该阶段为协议执行提供基础数据和模型支撑，生成相应的密钥，为用户的查询任务做准备.

2) 初始化阶段.该阶段初始化系统模型的各个计算参数，并计算SSC-AGG算法的初始化，为后续关键的迭代聚合做准备.

3) 迭代聚合阶段.该阶段进行核心的计算，通过Ω轮的迭代计算得到理想分类的密态结果.

4) 用户接收阶段.该阶段用户本地做最后的简单计算，获取最终的分类查询结果.

Table 3 Overview of FPCBC

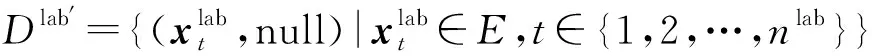
2) 初始化阶段.确定进行迭代聚合的总轮数Ω和聚合算法中的超参数α,ρ等;与此同时，在进行对弱结果的迭代聚合之前，初始化一些变量.

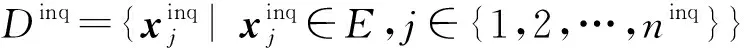
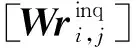
步骤2.在预处理之后，服务器A获得了模型对Dlab′的推理结果，即可计算：

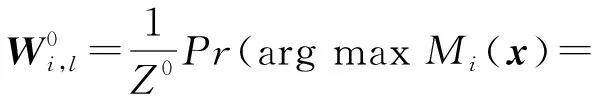
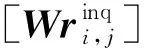
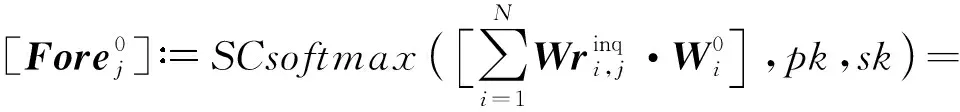
3) 迭代聚合阶段.根据初始化阶段得到的数据继续进行总轮数为Ω的迭代计算得到理想的密态结果，对于第τ轮：

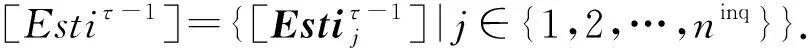
如果boolean=true，服务器A计算

如果boolean=false，服务器A计算

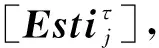
Cor=SCspear(Wτ -1,[Estiτ],pk,sk),

其中Cor={Cori|i∈{1,2,…,N}}，最后计算

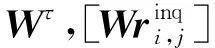
[F]

[Foreτ]SCsoftmax([F],pk,sk)=

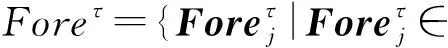
[ForeΩ]⊙[K]=[ForeΩ+K]，

并将结果发送给服务器B并解密，服务器A，B将分别持有的K和ForeΩ+K发送给用户.

4) 用户接收阶段.用户接收到双服务器发送来的结果，进行简单的计算去除盲化随机数:ForeΩ+K-K=ForeΩ，最后即可求得众包推理聚合出的分类结果:Result=arg max(ForeΩ).

4.3 安全分析

定理1.FPCBC训练数据集隐私安全.FPCBC方案不会泄露机器学习模型训练的数据集.

证明. 在我们的方案中，唯一需要进行机器学习模型训练的是边缘参与方，而且各个边缘参与方根据私有数据在本地进行训练，不会共享数据，因此根据分布式联邦学习数据不动的特点，其训练数据的保密性自然得到了保证.

证毕.

定理2.FPCBC数据和分类结果隐私安全.FPCBC方案在半诚实和服务器不合谋的前提下是数据和分类结果隐私安全的，根据3.2节的安全内容定义说明，系统面对任何一个半诚实的腐败方(边缘参与方、服务器A和服务器B)，用户的数据Dinq和最终结果Result在众包系统分类的过程中不会泄露.

证明.如安全实验所述，在我们的方案中分为3种可能腐败方：边缘参与方腐败、服务器A腐败和服务器B腐败，因此我们通过考虑下面的方法来证明定理2.

1) 数据隐私安全

我们通过证明:现实腐败方的视图与理想世界中腐败方的视图具有计算不可区分性的标准化论证法来论证定理2的数据隐私安全.

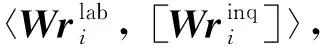
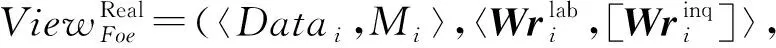
其中random表示随机带.我们生成模拟器S可以获得真实视图的输入输出，并模拟出理想世界的腐败方视图:

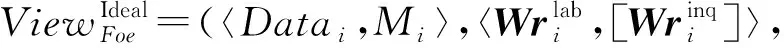
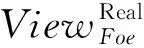
模拟器S：

① 获取数据集Datai，并训练出弱模型.

② 获取数据集Dlab′,[Dinq]，并计算出它们经过弱模型推理的结果.

③ 生成与[Dinq]等大的随机数据R.

系统执行过程中，服务器A只会接收到密文[Dinq]，因此与边缘参与方腐败情况相似，满足数据隐私安全.服务器B不会获得与用户查询数据直接相关的数据，不存在数据隐私安全的问题.因此，可证得FPCBC满足数据隐私安全.

2) 分类结果隐私安全

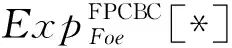
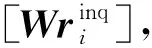
因此可证得FPCBC满足分类结果隐私安全.

证毕.

5 实验性能及分析

本节对基于众包聚合的联邦学习隐私保护分类系统的性能进行评估和模拟.在系统实现过程中，我们从系统的3个不同方面进行实验分析：用户数据加密、边缘参与方密态推理和双服务器迭代聚合.实验在AMD EPYC 7302 16-Core CPU，32 G RAM的64位Windows10操作系统计算机上进行.

目前关于安全分类推理的方案大都是基于训练出理想模型的解决思路，与我们的系统没有直接的可比性.因此，我们对FPCBC自身进行实验数据分析.

5.1 实验相关参数

我们使用手写数字图像数据集MNIST[35]和CryptoNets[22]神经网络进行系统测试.MNIST包含了0～9分类的手写数字，一共由60 000张手写数字图像作为训练集和10 000张手写数字图像作为测试集，如图6所示.每张图像都由28×28个像素组成且每个像素取值为0～255的灰度值.本实验进行模拟的思路是让边缘参与方利用明文训练集进行模型的训练，再用10 000张测试集图像来测试用户数据分类准确度.边缘参与方使用Dowlin团队的CryptoNets架构来训练模型，该架构源码模型已完成了基于MNIST训练集在明文下的训练且准确率已经达到较高的可信度：98%～99%.为了配合验证我们提出的系统可以实现弱到强结果的密态聚合，通过更改训练好的模型参数来预降低推理准确率.更改20种神经网络来生成20个不同低准确率的模型，并分别取5,10和20个一组来模拟N=5,N=10和N=20个边缘参与方，如图7所示.

Fig. 6 Pictures of MNIST handwriting dataset图6 MNIST手写数据集图片

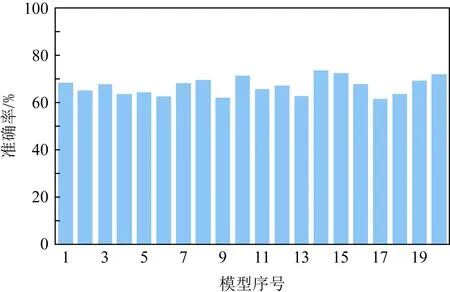
Fig. 7 Weak model accuracy of edge participants图7 边缘参与方弱模型准确率

实验的加密使用同态加密代码库SEAL，在使用Bos团队[26]的同态加密方案之前需要对明文数据进行编码处理，编码的目的是将实数范围的明文映射到适用于加密方案的环域，从而保证计算得到的解密结果是正确的，详细的编码加密过程请参考文献[22].

c

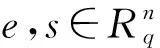
数据的编码需要5对参数联合使用，加密方案中选取的5对参数q，t，如表4所示.此外，由于编码技术使用中国剩余定理，编码的过程可以实现单指令多数据(SIMD)的批处理操作，这就意味着相同批次的时间内可以编码加密一批图像数据，其批处理的数量大小取决于n，实验中取n=4 096，此时批处理的数据量也为4 096.

Table 4 Parameters of Homomorphic Encryption Scheme

5.2 数据编码加密开销

我们将MNIST的测试集充当用户的查询数据，我们测试了ninq=4 000,7 000,10 000时用户加密和编码的时间开销.如图8(a)所示，用户加密3组不同数量图片分别需要32.5 s，62.3 s和96.6 s，虽然看上去时间开销较大，但由于是批处理，所以平均每张图片的效率十分乐观.此外，图8(b)显示了对这些图像进行编码处理的时间开销，对3组数据分析计算，平均每个图像的编码时间约为0.124 s.

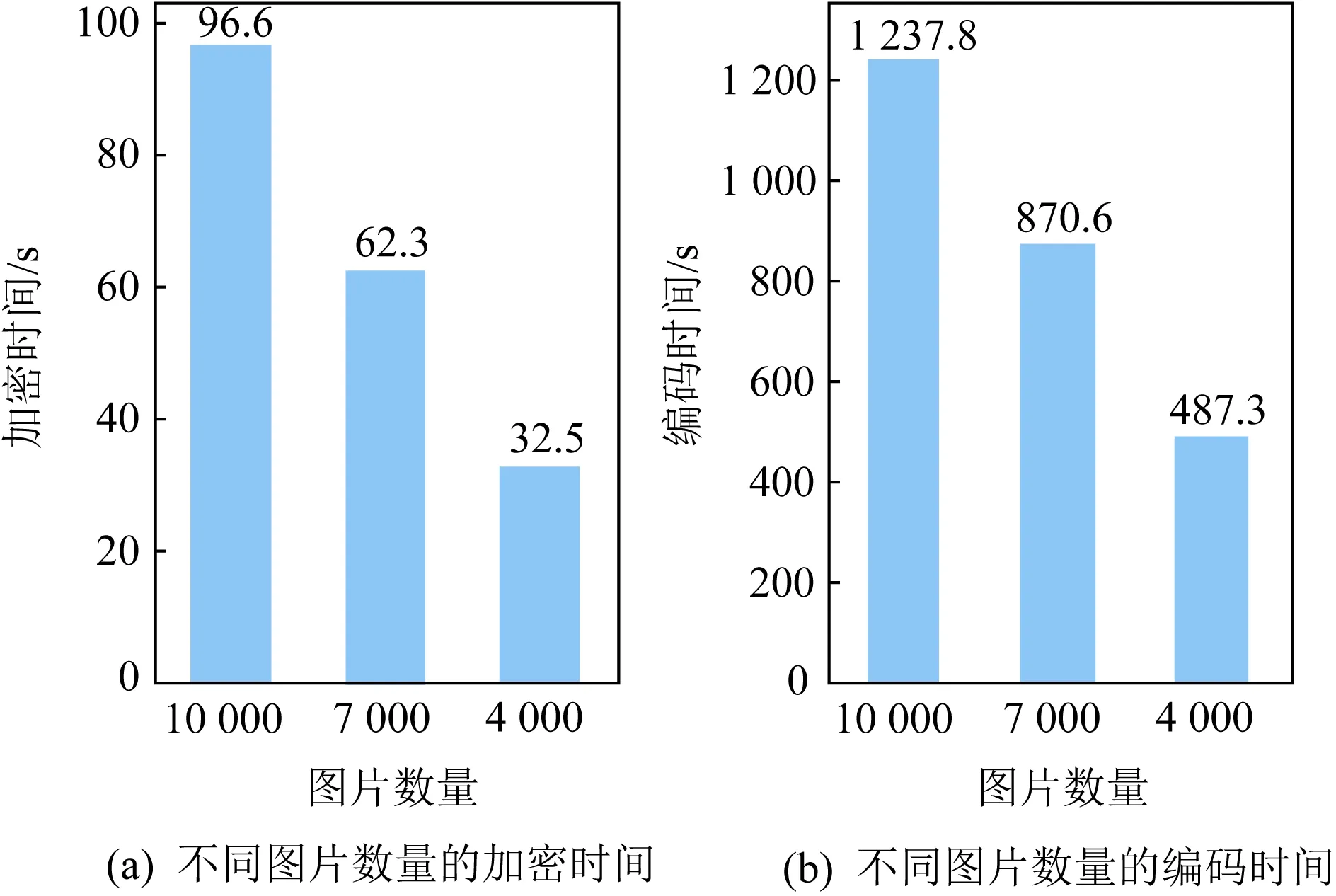
Fig. 8 Time overhead for different sets of image encryption and encoding图8 不同组图像加密和编码的时间开销

5.3 推理与聚合处理开销

基于之前编码加密的4 000，7 000，10 000张图片，将其交给图7中20个不同准确率的CryptoNets模型进行推理，来模拟边缘参与方推理得到弱结果的过程.由于FPCBC在执行过程中，边缘参与方的推理是并行操作，我们计算其平均推理时间如表5所示:

Table 5 Average Inference Time of Neural Network

我们从MNIST的训练集中随机抽取nlab=300和nlab=600个数据作为服务器A持有的小型公开数据集Dlab，在双服务器通过交互实现对弱结果的迭代聚合中，表6显示了对4 000，7 000，10 000个数据进行每轮安全聚合计算的平均时间开销，不难发现聚合过程的时间成本还是比较大的.

Table 6 Average Time of Aggregation per Round

同态加密需要巨大的时间开销是公认的缺点，这也是很难将该技术投入到实际应用的原因，但是本实验中使用的同态加密算法，对于明文数乘密文、数加密文的运算不必做额外的加密和密文的加乘运算[22]，因此可以大大减少同态加密带来的计算时间开销.通过对图8和表5、表6分析可知，用户和边缘参与方进行操作的时间也都在几十到几百秒不等，而且整个方案的核心时间开销在双服务进行安全聚合迭代的过程，为了得到高准确度的结果，我们往往需要进行多轮迭代操作.不过我们进行的是批处理，也就是说这些开销是对几千甚至上万张图片处理的时间开销总和，那么平均每张图片的开销则非常少，因此平均效率十分乐观.

5.4 分类准确率对比

根据图7可以计算出当N=5,10和20时的平均弱结果统计图，并且我们基于nlab=300和nlab=600在3种不同N的前提下对最后聚合的平均准确度进行了对比，如图9所示.

图9(a)和图9(b)说明基于nlab=300和nlab=600聚合出的正确率都达到了80%以上，与聚合前的正确率相比不难发现我们的方案是可以显著提高准确率且可行的.通过对2个图的比较，nlab=600比nlab=300的平均正确率偏高一些，因此我们可以得到这样的结论：如果服务器A持有更大的小型公开数据集Dlab，则可以获取更高准确率的预测，且当有更多的边缘参与方N时，越容易快速聚合出较高准确率的分类结果.

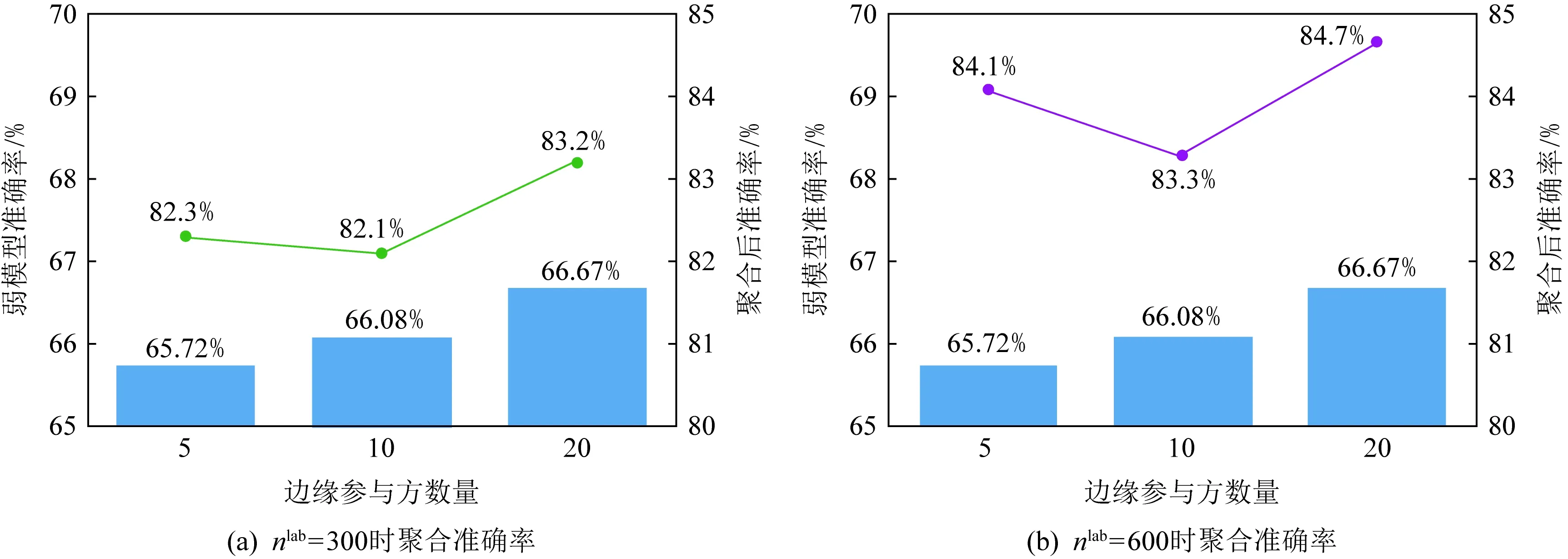
Fig. 9 Classification inference accuracy distribution before and after aggregation图9 聚合前后分类推理准确率分布

我们的实验只是基于一种同态加密神经网络，而这对于FPCBC来讲是灵活可变的，也就是说，如果有更优化的同态加密方案，则效率会更加理想.此外，我们的方案与传统分类推理不同的是，用户、边缘参与方和服务器完全是独立计算的，即用户和边缘参与方将自己的计算任务完成之后完全可以处于离线状态，不需要一直保持连续的通信，即使安全聚合的过程时间开销巨大，但不会占用用户和边缘参与方的资源，且若服务器拥有更高的计算能力，则整体效率也会有提升.综上所述，FPCBC也具有很强的自由度和鲁棒性.

6 结束语

本文提出了一种基于众包聚合的联邦学习隐私保护分类系统.为了实现弱结果的安全密态聚合，我们依靠双服务器设计了服务器安全交互算法.此外，同态加密和双服务器交互算法的存在使系统不会泄露任何用户查询的敏感数据，从而使得我们的方案有更加可靠和更高程度的隐私安全保障.在我们的系统中，只需要服务器从边缘参与方收集分类查询的弱结果，不需要获取机器学习模型和数据集，由此可以保证边缘参与方的隐私.双服务器通过安全交互聚合算法，根据统计学原理对弱推理结果聚合来提供更准确、更安全的分类预测服务.我们将众包、联邦学习思想与密码学技术相结合，提出了对用户和边缘参与方都十分友好的应用系统，即用户和边缘参与方的计算量需求较小、系统鲁棒性强的特点.其中核心计算量都交给了服务器来执行，因此服务器计算能力的强弱直接影响我们系统的效率.作为未来的方向，我们将专注于设计更小通信量的方案，并提升系统预测的准确率.

作者贡献声明：金歌负责创新方法的提出和论文的撰写；魏晓超负责方案分析和论文修改；魏森茂负责实验的构思和改进；王皓负责方案分析和论文润色.