例析数学知识在高中物理解题中的应用
江苏苏州市吴江中学(215200)王金淼
高中物理对很多学生来讲是一门充满挑战的学科,这不仅因为物理解题过程比较复杂,还因为物理解题过程中会用到很多数学知识,而进入高中阶段,数学知识较抽象,这无疑给物理问题的解决带来了较大的麻烦。下面笔者结合教学实践对数学知识在高中物理解题中的应用进行分析。
一、对数在物理解题中的应用
在高中阶段,对数和对数函数是数学考查的重要知识点,同时,对数知识在物理解题中也有重要的应用。
[例1]在研究太阳系八大行星的运动问题中,通常将它们的运动轨道近似看作圆轨道。下列4幅图是某研究小组为描述行星运动轨道规律而作的图像,其中T和R分别指行星轨道的周期和相应的半径,T0和R0分别指水星轨道的周期和相应的半径,则4幅图中描绘正确的是( )。

图1


小结:本题主要涉及对数、一次函数和绘制图像等,在考查物理知识的同时,考查了学生运用数学知识解决物理问题的能力。
二、圆的性质在物理解题中的应用
圆的性质乍一看好似与物理解题没什么关系,但在具体解题过程中,如果能够巧妙应用,则能让物理问题的解决变得直观便捷。尤其是在解决力学的分力与合力问题时,圆的性质用得更多。
[例2]如图2 所示,小物块在拉力F的作用下沿着光滑的半圆形弧面从B点缓慢运动到A点。整个过程中,力F的方向始终沿着半圆形弧面的切线方向。以下结论正确的是( )。

图2
A.拉力F逐渐变小
B.拉力F先变大后变小
C.小物块受到的支持力逐渐变大
D.小物块受到的支持力先变小后变大
解析:如图3 甲所示,对小物块进行受力分析,其中支持力FN与拉力F的方向始终垂直,由受力平衡可知FN和F的合力F合与小物块的重力等大反向。可画出力的矢量三角形的外接圆如图3 乙所示,由图可知,外接圆的直径表示合力F合,根据圆的性质可知,支持力FN先变大后变小,力F逐渐变小。

图3
小结:数学是解决物理问题的基本工具之一,在学习过程中,一定要注意总结归纳这些常用方法。
三、不等式在物理解题中的应用
物理问题中常会遇到需要求极值的情况,这类题通常是由于某个物理量受到取值或者物理规律的限制,而在某一个区间内变化,这种情况在表现形式上与数学中的不等式类似。在实际解题过程中,可以利用不等式求物理题中的极值。
[例3]如图4所示是一个串联电路,其中电源电动势和电源的内阻分别为E和r,R1是定值电阻,R2是可变电阻。在这个电路中,当可变电阻R2取何值时其消耗的功率最大?并求出消耗功率的最大值。

图4
解析:利用等效法,可将定值电阻R1视为电源的内阻,此时电路变为电动势为E、内阻为R1+r的电源外接一个可变电阻R2。可变电阻R2消耗的功率就是等效电源的输出功率,根据功率公式可得:


小结:解决此类问题最常用的工具是不等式极值的求解方法,如若a+b≥,当a=b时,a+b取最小值,ab取最大值。在物理问题中,如果需要求极值,可以优先考虑用不等式的性质求解。
四、相似三角形在物理解题中的应用
在力学问题中,常会考查三力平衡的相关知识,常规的解题方法是利用力的合成与分解,但通常情况下这种方法较为复杂,那么有什么方法可以让这类问题的求解变得简单呢?我们先来看看下面的例题。
[例4]如图5 所示,一质量不计的轻质细杆OA可绕O点自由转动,竖直细杆OB顶端安装有一理想定滑轮。在A点悬挂一重力为G的重物,系在A端的轻绳绕过B点处的定滑轮用力F拉动。当细杆OA从与OB重合处缓慢顺时针放下,∠AOB由0°变为180°的过程中,下列判断正确的是( )。
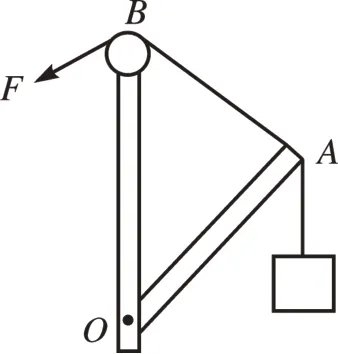
图5
A.拉力F越来越大,但不会超过2G
B.细杆OA所受压力大小始终为G
C.拉力F先增大后减小
D.细杆OA所受压力先减小后增大
解析:对细杆OA的A端进行受力分析,可得如图6 所示的示意图。由几何知识可知,△OAB与力的矢量三角形是相似图形,根据相似三角形的性质可得:
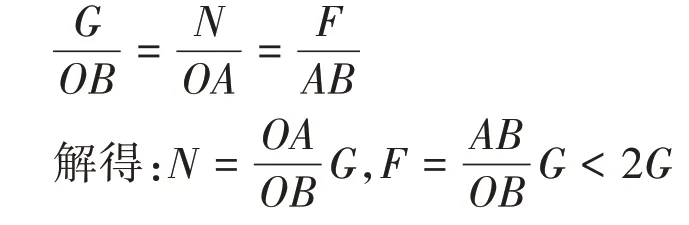

图6
因为在细杆OA放下的过程中,AB的长度在不断增加,所以拉力F不断变大;而OA和OB的长度不变,因此只有选项A,B正确。
小结:数学知识在物理中有妙用,最大优点是能够使本来复杂的分析过程变得直观,相似三角形在本例中起到的作用就是如此。
五、一元二次方程在物理解题中的应用
在运动学问题中,我们列出的公式常会出现一元二次方程,那么是否可以利用一元二次方程的一些性质来简化物理问题的解题过程呢?回答是肯定的。其中常用的有以下两个:①在一元二次方程ax2+bx+c=0中,根与系数存在一定关系,即x1+x2=②根的判别式Δ=b2-4ac。巧妙利用以上两个性质,可以简化解题过程。
[例5]小明坐公交车去上学,在距离公交车站60 m时发现要乘坐的公交车正以a=1 m/s2的加速度启动,于是他以速度v0追赶公交车并同时呼喊让公交车司机停车。若只有当小明距离公交车小于20 m 且持续呼喊2 s才能保证公交车司机能够收到他的停车请求。问:
(1)小明的奔跑速度v0至少应为多少?
(2)若v0=10 m/s,则小明距离公交车最近的距离为多少?
解析:(1)设小明到达距离公交车20 m 处时用时Ts,根据位移公式可得:

代入a=1 m/s2,化简后可得:
T2-2v0T+80=0
上式为关于T的一元二次方程,设T1、T2为该一元二次方程的两个根,由一元二次方程的根与系数的关系可得:
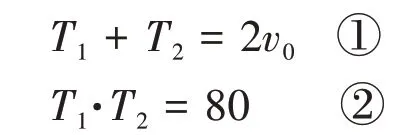
因为小明想要坐上公交车,他与公交车的距离应小于20 m且持续呼喊2 s才可以,由此可得:

联立①②③三式可得小明奔跑的最小速度
v最小=9 m/s
(2)若v0=10 m/s,则经过时间t后小明与公交车的距离为:

由上式可知,当t=10 s时,d取最小值,可得d最小=10 m。
[例6]在一次实验探究活动中,小明得到一个阻值为5 Ω的小灯泡、一个最大阻值为10 Ω的滑动变阻器和一个内阻不计、电压为2 V 的电源,另有开关一个、导线若干。他用上述器材组成一个串联电路后,调节滑动变阻器,问:若想滑动变阻器接入电路部分消耗的功率最大,则接入部分的阻值应为多大?
解析:设滑动变阻器接入电路部分的阻值为R,其消耗的功率为P,则可得:

整理上式可得到一个关于R的一元二次方程
PR2+(10P-4)R+25P=0
因为电阻应为实数,故上式应有实数解,由此可得:
Δ=b2-4ac=(10P-4)2-4P× 25P=16-80P≥0
解得P≤0.2 W,故滑动变阻器接入电路部分消耗的功率的最大值为0.2 W。
将P=0.2 W 代入PR2+(10P-4)R+25P=0可得R=5 Ω。
小结:以上两个例题的解法有很多,若作比较就会发现,利用一元二次方程根与系数的关系及根的判别式进行解题,解题思路较为清晰,解题步骤也相对简单。
综上,高中物理解题想要便捷高效,离不开数学知识的有效应用。为了达到理想的解题效果,在平时教与学的过程中,教师和学生都要有意识地加强物理知识与数学知识的融合,注重归纳和反思。

