圆锥曲线焦点弦的特别结论及应用

四川宜宾市叙州区第二中学校（644600）严肃

（注：当双曲线的焦点弦交于同支时也适合此公式；抛物线的焦点弦同样适合，只是在抛物线中离心率取1即可，其证明同椭圆。）

点评：本题是直线与椭圆的综合题，通过向量的关系求坐标。解法一，由椭圆的方程可得到B，F的坐标，求出直线BF的方程，与椭圆联立求出A的坐标，进而求出向量，由题意得到结果。不难看出，这种传统解法计算烦琐，容易出错。而解法二则直接通过公式，两步得出结果，省去了繁杂的计算。

点评：本题主要考查椭圆的性质，涉及向量的坐标运算性质，考查学生的运算能力。解法一通过焦点三角形，利用椭圆的定义以及余弦定理，再利用向量坐标，计算烦琐，容易出错。而解法二巧妙，易得结果。

小结：这两道题主要考查的是圆锥曲线焦点弦所在直线的倾斜角和离心率以及焦半径之间的关系，运用上述结论1，省去了繁杂的计算。

（注：过焦点且垂直于焦点所在轴的焦点弦称为通径。椭圆和双曲线的通径长是，抛物线的通径长是2p。双曲线的焦点弦交于同支时也适合此公式，使用时为保证弦长为正数，加上绝对值即可；抛物线的焦点弦同样适合，只是在抛物线中离心率取“1”即可，其证明同椭圆。）

［例3］已知椭圆C的焦点为F1(-1,0)，F2(1,0)，过F2的直线与C交于A，B两点。若|AF2|=2|F2B|，|A B|=|BF1|，则C的方程为（）。

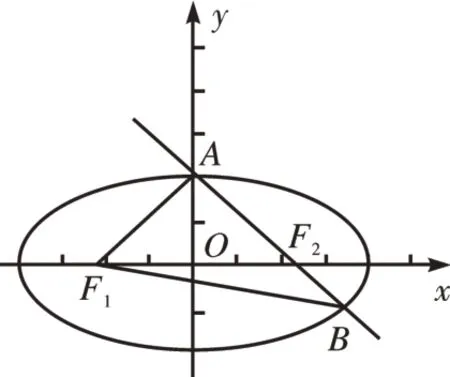
图6

解法一：由已知可设|F2B|=n，则|AF2|=2n，|BF1|=|AB|=3n，由椭圆的定义有2a=|BF1|+|BF2|=4n，则|AF1|=2a-|AF2|=2n，在△AF1B中，由余弦定理，得

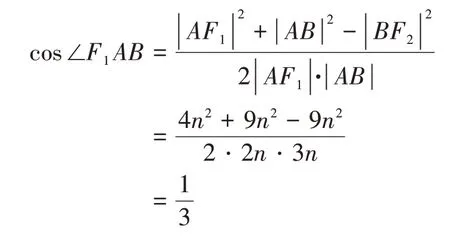
在△AF1F2中，由余弦定理得

点评：本题考查了直线和椭圆的基本性质以及椭圆的定义、椭圆的方程和余弦定理的应用，考查了学生的数学运算能力。解法一通过设|F2B|=n，利用椭圆的定义分别表示出|AF2|=2n，|B F1|=|AB|=3n，又在△AF1B与△AF1F2中利用余弦定理得出n的值，从而求出a的值，再利用b2=a2-c2，最后得到所求方程。整个过程计算量太大，对比解法二，利用焦点弦长公式，大大减少了运算量。显然对于考生来说，运用解法二更好。

［例4］斜率为的直线过抛物线C：y2=4x的焦点，且与C交于A，B两点，则||AB=___________。

解法一：∵抛物线的方程为y2=4x，∴抛物线的焦点F坐标为F(1,0)，

点评：本题主要考查抛物线的简单几何性质，直线与抛物线的位置关系的应用，考查学生的计算能力。解法一和解法二都是由题意求出直线的方程，联立直线和抛物线方程，利用抛物线的性质转化求解得出结果，而解法三则只用了一下弦长公式就一步到位，真正达到“小题小做”的目的。

［例5］已知抛物线C：y2=2px(p＞0,p≠4)，过点A(2,0)且斜率为k的直线与抛物线C相交于P，Q两点。

（Ⅰ）设点B在x轴上，分别记直线PB，QB的斜率为k1，k2。若k1+k2=0，求点B的坐标；

（Ⅱ）过抛物线C的焦点F作直线PQ的平行线与抛物线C相交于M，N两点，求的值。

解：（Ⅰ）略。

（Ⅱ）解法一：由题意y2=2px与y=k(x-2)，

联立可得k2x2-(4k2+2p)x+4k2=0，即xQ+

如图8 所示，不妨设∠MFA=θ，即有k=tanθ，因为PQ ∥MN，即∠PAP′=θ。

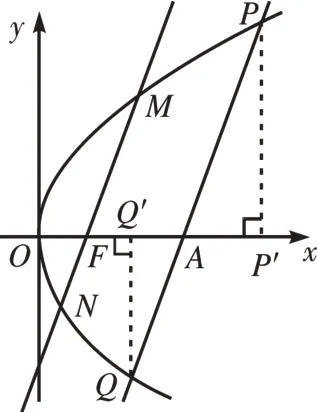
图8

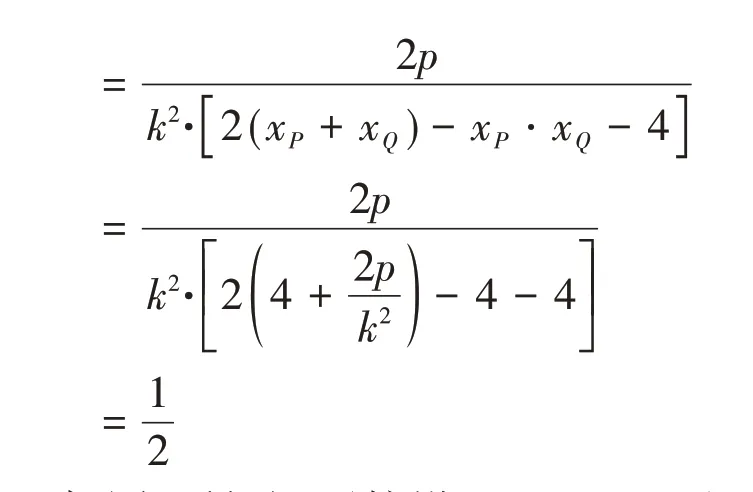
解法二：如图8 所示，不妨设∠MFA=θ，即有k=tanθ因为PQ ∥MN，即∠PAP′=θ。

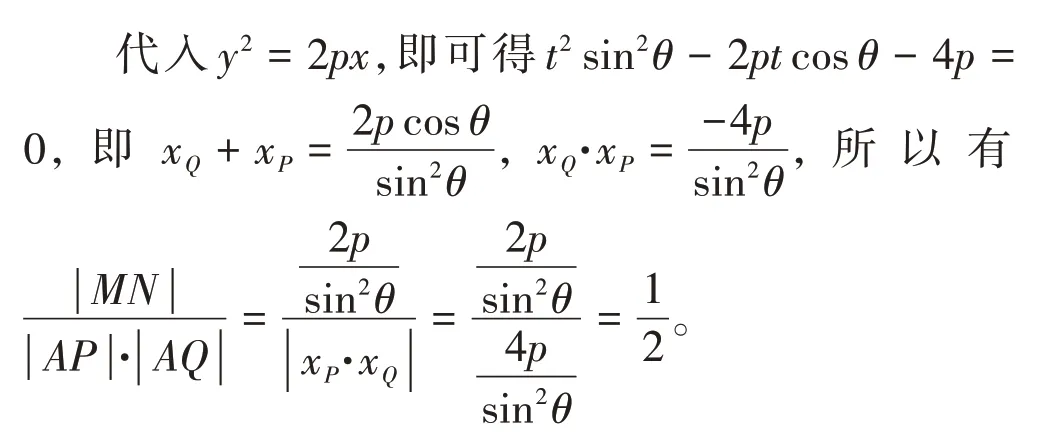
小结：这两道题主要考查的是圆锥曲线焦点弦所在直线的倾斜角和焦点弦之间的关系，解这类题型的方法有多种，运用结论2，无疑省去了繁杂的计算，很容易就能得出结果。