基于核心素养的导学案设计研究——以“线面垂直的判定”教学为例

广东广州市第八十六中学（510700）魏勇

《普通高中数学课程标准（2017 年版）》中提到，高中数学课程以学生发展为本，落实立德树人根本任务，培育科学精神和创新意识，提升数学学科核心素养。教师应将这项目标全面渗透到教学活动中，进而使学生的思维能力得到有效提升，使学生的潜力得到有效挖掘，使学生的发展需求得到满足。

数学导学案是一种比较重要的学习方案，它能够引导学生有针对性地学习，使学生的学习能力得到有效提升。对于学生的学习来说，导学案发挥着十分重要的作用，因此数学教师应该在导学案设计中有意识地落实核心素养。

下面以“线面垂直的判定”教学为例，谈谈如何将数学学科核心素养渗透到导学案设计中。

一、教学目标

1.利用直观感知对直线与平面垂直的画法形成正确的认识。

2.利用“直观感知—动手操作—思辨论证”的认识方法对直线与平面垂直的定理进行判断。

3.熟练掌握直线与平面垂直的判定方法。

4.能够从实际生活中找出几何图形之间的联系，提升逻辑思维能力和观察能力。

二、教学过程

（一）发放导学案，引导学生预习

教师发放导学案，引导学生课前预习完成导学案并由小组合作检验，课堂上进行展示、质疑，教师进行点评。

附：导学案（局部）

一、学习目标（略）

二、重点与难点

重点：直线与平面垂直的定义；

难点：直线与平面垂直的判定定理的探究。

三、学习过程

（一）直线与平面垂直的定义

有关概念：直线l叫平面α的__________，平面α叫作直线l的__________。直线与平面垂直时，它们唯一的公共点P叫作__________。

（二）直线与平面垂直的判定定理

（三）例题讲解

［例1］如图3 所示，在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥平面ABCD，PA=AD，点M是PD的中点。求 证：（1）BD⊥平面PAC；（2）AM⊥平面PDC。

图3

总结：

（1）证明线面垂直转化为证明_____________；

（2）证明异面直线垂直转化为证明_____________。

［例2］如图4 三棱锥V-ABC中，VA=VC，AB=BC，K是AC的中点。

图4

（1）求证：AC⊥平面VKB；

（2）求证：VB⊥AC。

思路：（1）

（二）创设情境，建构概念

知识点：直线与平面垂直的定义。

复习1：直线与平面有几种位置关系？

生1：平行、相交、线在面内。

复习2：为什么没有直线与平面垂直呢？

生2：垂直是相交的一种特殊情况。

引入课题：既然“垂直”那么重要，我们今天就来一起研究“直线与平面垂直”。

问题1：在阳光下对垂直插在地面上的旗杆AB及其在地面上的影子BC进行仔细的观察，这时能够观察到随着时间的变化，影子的位置也在不断移动，而旗杆所在的直线AB与其影子所在的直线BC的夹角随着时间的变化是不是也会产生变化？角度又是如何变化的？

生3：旗杆所在的直线AB与其影子所在的直线BC的夹角始终保持不变，都是直角。

问题2：旗杆AB和地面上任意一条不过旗杆底部B的直线m之间形成怎样的位置关系？

生4：旗杆AB和地面上任意一条不过旗杆底部B的直线m都垂直。

问题3：通过旗杆AB和地面垂直、旗杆AB和地面上任意一条直线垂直关系的思考，哪位同学可以说出直线与平面垂直的定义？

生5：如果直线l与平面α内的任意一条直线都垂直，我们就说直线l与平面α互相垂直。直线l叫作平面α的垂线，平面α叫作直线l的垂面。直线与平面垂直时，它们唯一的公共点P叫作垂足。

（三）实验探究，操作确认

实验探究：准备三角形纸片，如图5，在△ABC的顶点A将纸片翻过来折起来，折痕AD，然后将其放到桌面上（BD，DC和桌面接触）。

图5

问题4：折痕AD与桌面一定垂直吗？

生6：不一定。

问题5：怎样翻折才能使折痕AD与桌面垂直？

学生7：折痕AD⊥BC时，AD与桌面垂直。（如图6和图7）

图6

图7

问题6：由折痕AD⊥BC，翻折之后的垂直关系AD⊥CD，AD⊥BD发生变化吗？由此你能得到什么结论？

生8：由折痕AD⊥BC可知，翻折之后AD⊥CD，AD⊥BD，由此可以得到直线AD与桌面是垂直关系。

问题7：哪位同学可以总结归纳直线与平面垂直的判定定理？

生9：如果一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直。

（四）数学引用，巩固新知

［例1］如图8，在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥平面ABCD，PA=AD，点M是PD的中点。求证：（1）BD⊥平面PAC；（2）AM⊥平面PDC。

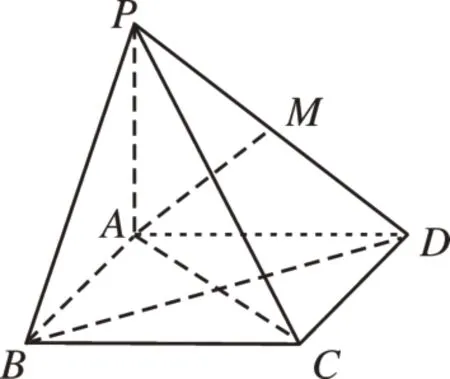
图8

思路：（1）要证BD⊥平面PAC，即证BD⊥AC（已知），BD⊥PA；

要证BD⊥PA，即证PA⊥面ABCD（已知）。

（2）要证AM⊥平面PDC，即证AM⊥PD，AM⊥CD；

要证AM⊥PD，即证PA=AD（已知）且PM=DM；

要证AM⊥CD，即证CD⊥面PAD。

总结：

（1）证明线面垂直转化为证明线线垂直；

（2）证明异面直线垂直转化为证明线面垂直。

设计意图：理解直线与平面垂直的判定定理，掌握直线和平面垂直的本质，即直线和平面内的两条相交直线都垂直，从而将线面垂直问题转换为线线垂直问题。线线垂直可分为共面垂直和异面垂直，共面垂直属于平面几何问题，异面垂直可转化为线面垂直。通过倒推的方式让学生理解立体几何证明的思维模式，培养学生的逻辑推理能力。

［例2］如图9，三棱锥V-ABC中，VA=VC，AB=BC，K是AC的中点。

图9

（1）求证：AC⊥平面VKB；（2）求证：VB⊥AC。

思路：（1）要证AC⊥平面VKB，即证AC⊥VK，AC⊥BK；

要证AC⊥VK，即证VA=VC，AK=CK（已知）；

要证AC⊥BK，即证BA=BC，AK=CK（已知）。

（2）要证VB⊥AC，即证AC⊥平面VKB（已知）。

设计意图：理解并掌握共面垂直的常见类型，矩形、正方形的邻边，菱形的对角线，等腰三角形的中线等；了解异面直线垂直的证明方法。

三、导学案设计反思

（一）导学案的学习目标需立足“四基”

提升学生的数学学科核心素养，要通过丰富学生的数学基本活动经验，培养学生的数学基本思想、基本技能以及基本知识来实现。如果没有“四基”，很难提升学生的数学学科核心素养。在设计导学案时，需要引导学生对数学基本知识形成全面的了解，能够领悟其中蕴含的基本思想、基本技能等，只有这样才能够有效地提升学生的数学学科核心素养。引导学生根据直观感知及已有经验（两条相交直线确定一个平面），进行合情推理，获得直线与平面垂直的判定定理：如果一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直。

（二）导学案需创设合适的情境

只有在合适的数学情境中，学生才能进行深度思考与交流，学生的数学学科核心素养才能得到提升。本文主要围绕直线与平面垂直的定义、直线与平面垂直的判定定理来设计导学案。学生通过完成导学案能够使自身的数学学科核心素养得到显著提升。教师需要结合学生的实际需求，为学生创建良好的学习环境，引导学生合理利用数学语言和数学思想，解决数学学习中遇到的问题。只有创设合适的情境，学生才能够将新旧知识联系在一起，进而对新知识有更加全面的理解，同时激活已有经验，建立新旧知识之间的联系。有研究者认为，学生只有在具体的情境中完成知识的建构，才会认识到知识的价值，这是学科核心素养形成的前提。

（三）导学案应重视探究活动

要提升学生的数学学科核心素养，最重要的就是开展数学探究活动。本节课的导学案结合两个探究活动展开设计。通过对地面和旗杆的位置关系进行观察，进而总结出线面垂直的概念；通过对地面垂直和三角形折叠的折线之间的关系开展实验，进一步总结出直线和平面垂直的判定定理。

教师要发挥主导作用，从任务确定到任务探究、任务分配、流程安排到活动组织、成果展示、结果评价等诸多环节，都要去设计和安排，保证探究活动的有效开展，减少探究的盲目性，避免课堂的无序性，准确把握学生探究学习的深度。

（四）导学案应着力引导学生思考

数学教学中，教师组织学生展开数学活动，能使学生的思维能力得到提升，使学生懂得运用数学思维解决实际问题。教师应该充分发挥学生的主体作用，采取多样化的教学方式，促使学生更主动地学习。导学案的设计越贴近学生的思维，课堂就越能按照预设的主线前进。当然，有时也会遇到一些生成性问题，学生对某些例题可能会形成多种解题思路。学生学习过程中的生成性问题都是由学生原有经验与新知识之间的冲突形成的，是非常宝贵的教学资源。阅读自学、动手实践、独立思考、自主探究、合作交流、展示质疑等都是导学案的学习方式，教师应通过多种方式引导学生思考，以促进学生数学学科核心素养的发展。