用于特征选择的改进二进制蝙蝠算法
李占山, 沈琳睿, 阮 锟, 杨鑫凯,3
(1吉林大学 软件学院, 吉林 长春 130012;2.吉林大学 计算机科学与技术学院, 吉林 长春 130012;3.吉林大学 符号计算与知识工程教育部重点实验室, 吉林 长春 130012)
0 引 言
现实生活中存在各种各样的数据,如电子交易数据、新闻报道数据等。这些数据通常具有大量的特征,其中许多特征是不相关的或冗余的。这些不相关或冗余的特征可能会对机器学习算法造成负面影响,如增加模型学习时间、降低模型准确性[1]。特征选择作为一种常用的数据预处理方法,旨在去除不相关的、冗余的特征以提高模型的泛化性能,并节省资源。
根据子集搜索和评估过程,特征选择方法可以分为过滤式、包裹式和嵌入式[2]。过滤式方法不依赖于任何学习算法,而依赖于条件特征和类之间的相关性。包裹式方法根据使用分类器的表现,将特征删除或添加到特征子集中,这个过程会耗费较多资源。通常,包裹式方法比过滤式具有更好的分类性能,得出的特征子集往往更符合分类器的要求。
特征选择过程中的最优特征子集被证明是NP难问题。因此,对于高维数据,搜索最优特征子集是困难的。对于具有N个特征的数据集,其搜索空间随特征数呈指数增长[3]。因此,人们设计了许多搜索策略来提高特征选择的效率。由于元启发式方法拥有较强的全局搜索能力,在搜索空间中能够在快速找到接近最优的解,许多研究已经提出使用元启发式方法来解决特征选择问题[4]。例如,粒子群优化算法(PSO)、遗传算法(GA)、蚁群优化算法(ACO)、模拟退化算法(SA)等。
受蝙蝠回声定位行为的启发,Yang X S[5]提出一种新的元启发式算法----蝙蝠算法(BA)。该算法具有良好的收敛性和可靠性,Mirjalili S等[6]将BA的搜索策略运用到二进制搜索空间中,提出了二进制蝙蝠算法(BBA)。BBA采用V形传递函数,将蝙蝠个体的速度值映射为位置更新的概率值,从而将连续搜索空间中的搜索过程映射到二进制搜索空间。同时,BBA保持了BA参数少、收敛快、鲁棒性好的优点。
然而,BBA也存在一些问题,在BBA的种群更新过程中,传递函数不能依据种群的变化情况而调整。当蝙蝠个体快速移动到当前最优解位置后,个体速度趋于0,位置改变的概率趋于0。因此,BBA的二进制转化方案在面临搜索停滞的局面时,没有摆脱停滞的能力,不能对当前解空间进一步搜索,并且降低了算法的精度。
为了克服这一问题,文中提出一种改进的二进制蝙蝠算法(ABBA)。利用种群熵评价种群的相似程度,将种群熵计算因子加入传递函数,使传递函数适应算法收敛过程,增加在速度为 0 时个体的位置更新概率,使算法具有摆脱停滞的能力。
1 二进制蝙蝠算法(BBA)
二进制蝙蝠算法模拟了蝙蝠狩猎过程,蝙蝠在黑暗中通过回声定位来搜寻猎物并感知距离,在确定猎物的方向和位置后,通过改变脉冲发射的频率和响度进行进一步搜寻。二进制蝙蝠算法利用人工蝙蝠作为搜索代理,每个人工蝙蝠具有位置、速度和频率。当感知到猎物时就改变其响度与脉冲发射率,同时向猎物位置靠近。在搜寻猎物的过程中,认为位置最好的蝙蝠总是最靠近猎物的,猎物代表算法所要搜寻的最优解。
在BBA中,搜索代理在迭代过程中的频率与速度更新遵循
Fi=Fmin+(Fmax-Fmin)β,
(1)
vi(t+1)=vi(t)+(xi(t)-Gbest)Fi,
(2)
式中:Fi----个体i的频率;
β----[0,1]之间的随机数;
vi(t)----个体i在第t次迭代中的速度;
xi(t)----个体i在第t次迭代中的位置;
Gbest----当前最优个体的位置。
在二进制搜索空间中,改变位置需要通过位置向量中几个位的反转来实现。BBA中使用V形传递函数将搜索代理的速度向量按位转换成位置向量中每一位反转的概率,位置更新公式为:
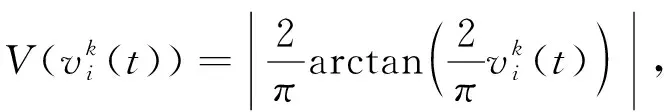
(3)

(4)
式中:xi(t)----第t次迭代中个体i的位置向量在第k维的值;
rand----[0,1]之间的随机数。
V形传递函数图像如图 1所示。
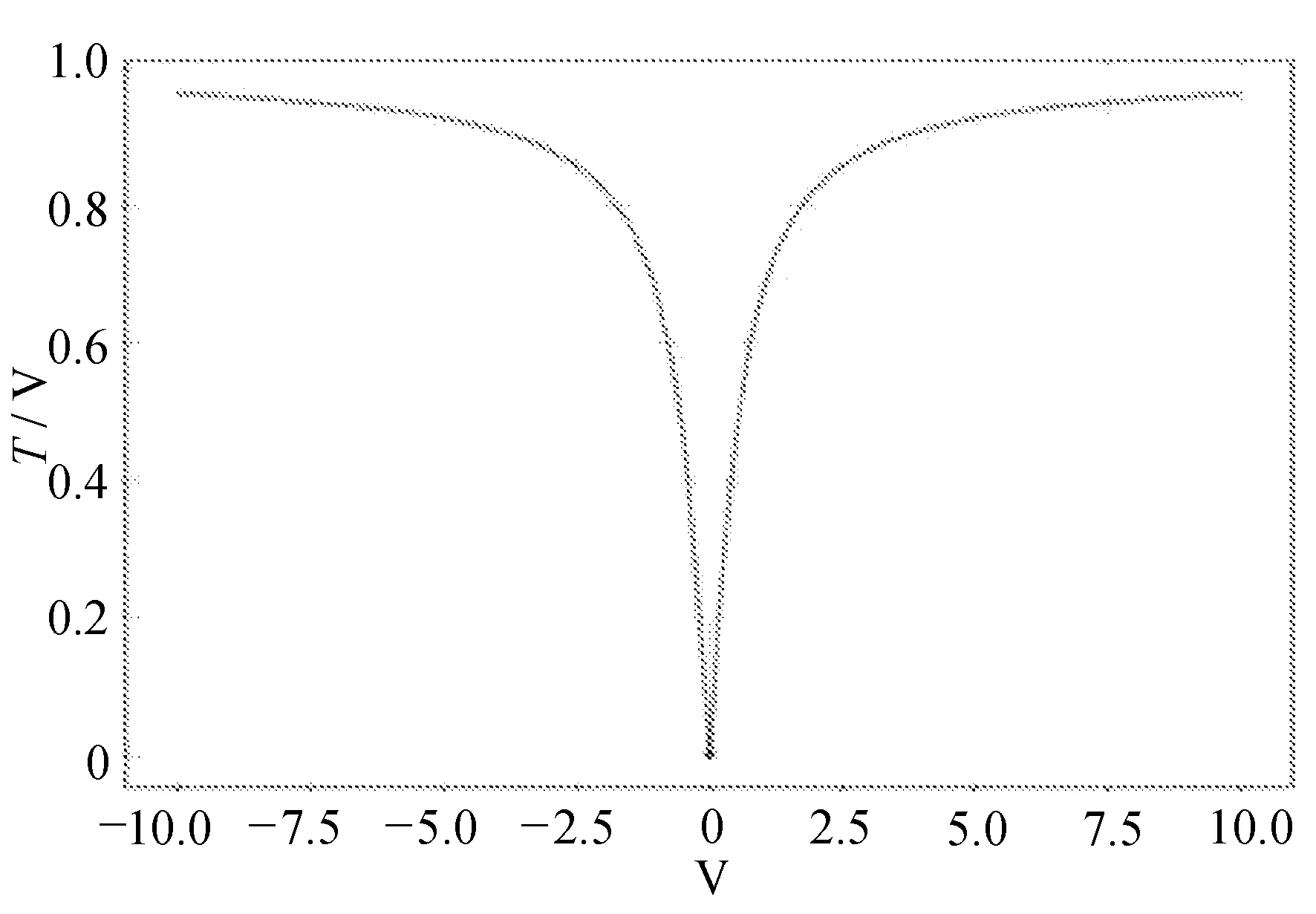
图1 V形传递函数图像
在个体速度接近0的时候,传递函数值也趋近于0,结合式(2)可知,在个体与猎物相近时,其位置改变的概率较小。
BBA的随机游走过程是通过与当前全局最优个体的位置向量交叉实现的。这个过程解释为:用Gbest位置向量中的一些维度与当前个体位置向量中的一些维度做交换。
在人工蝙蝠搜寻到更优的解决方案后,改变响度和脉冲频率。其更新公式为:
Ai(t+1)=αAi(t),
(5)
ri(t+1)=ri(0)[1-exp(-γt)],
(6)
式中:α,γ----[0,1]之间的参数。
式(5)和(6)表明,随着迭代次数的增加,响度将趋近于0,脉冲发射率将趋近于ri(0)。其中α相当于退火因子。
BBA算法的伪代码如下:
算法1 二进制蝙蝠算法:
1: 设置最大迭代次数tmax, 频率的上界和下界Fmax和Fmin, 响度和脉冲发射频率的递减因子α和γ, 脉冲发射率的最终值r(0);
2: 随机初始化蝙蝠种群的位置X_i (i=1,2,…,n), 速度Vi=0, 频率Fi, 脉冲发射率ri和响度Ai
3: while t 4: for i=1;i 5: 用式(1)与式(2)更新当前个体i的频率和速度 6: 用式(3)和式(4)更新当前个体i的位置 7: if (rand>ri) then 8: 在最佳解决方案中随机选择一个解决方案(Gbest) 9: 用Gbest改变位置向量的一些维度 10: end if 11: 利用随机飞行生成新解 12: if rand 13: 接受新的解决方案 14: 用式(5)和式(6)更新响度Ai和脉冲发射率ri 15: end if 16: end for 17: 给当前种群个体排序并选择出Gbest 18:end while 在BBA的收敛过程中,种群中个体逐渐靠近,当个体之间变得相近时,算法的收敛趋于成熟,此时个体进行位置更新的概率较低,出现停滞的现象,在陷入局部最优时没有跳出停滞的能力。针对这个问题,文中提出了改进的二进制蝙蝠算法。 对二进制蝙蝠算法的改进分为两部分: 1)利用种群熵对传递函数进行改进,使得算法在趋于停滞时具有跳出当前局面的可能; 2)对基于种群熵的传递函数进行改进,加快算法收敛。 两个改进点相互补充,共同作用,提高算法的精度。 BBA中利用V形传递函数将个体速度映射为位置改变的概率。当个体在当前最优解的附近时,个体的速度趋于0,根据V形传递函数,其位置改变的概率很小,容易陷入停滞的局面。此时,考虑将V形函数在0及其附近的函数值增大。而在个体未处于当前最优解附近时,尽量小地增加函数值。因此对函数值增加的量需要适应函数自变量的变化,在个体速度趋于0时,增加量越大;在个体速度值远离0时,增加量越小。根据二进制蝙蝠算法的搜索策略中式(2),个体与当前最优个体位置越靠近,种群间个体的一致程度越高,这个增加量应当越大;反之,个体间差别越大,这个增加量应当越小。 文中运用种群熵来反映演化过程中个体之间的多样性和一致性。种群熵是路景等[7]提出的一种反映种群多样性的量。要达到增加量能够根据种群变化进行相应调整的目的,要求种群熵可以反映当前的种群多样性程度,或者反映将来种群多样性程度的变化趋势。 定义:计算出当前第t代种群的平均适应度值favg,取当前种群中所有fi 定义第t代种群的熵为 其中, 根据定义可知,当种群中个体各不相同,即m=N时,种群熵取最大值Emax=logN;当种群中个体均相同,即m=1时,种群熵取最小值Emin=0。 种群熵反映了种群中不同类型个体的分布情况。种群中个体分类越多,分布越均匀,种群熵越大。通过种群熵与种群最大熵的比较,可以衡量出当前种群的多样性程度。令 显然,b∈[0,1]且b越大,种群中不同个体数目越多,即种群的多样性越大;反之,种群的多样性越小。 在种群逐渐趋于同一化的过程中,种群熵逐渐减小,而增加量需要增大。故新的传递函数公式为 b----种群熵定义中的种群较优个体多样性量化值。 新的传递函数图像如图2所示。 图2 种群熵改进的传递函数 通过比较新传递函数图像和原V形传递函数图像可以看出,新传递函数可以适应种群的变化情况,相应地调整位置改变的概率。当b减小时,增加量越大;b增大时,增加量越小。那么,当个体到达当前最优个体位置附近时,即使速度值为0,个体仍将获得一定的概率来改变位置,这样种群便具有跳出停滞的能力。 基于种群熵改进的传递函数是种群在趋于一致过程中具有一定阻力,在收敛趋于成熟的过程中不断有个体改变自身位置,向异于当前最优的方向改变,虽然增加了种群多样性,但在算法演化不足的情况下,会在一定程度上影响算法的收敛速度以及算法精度。因此,文中提出对基于种群熵传递函数改进的辅助改进点。 根据BBA的改进策略,蝙蝠个体只有在找到优于当前最优解的位置后才会改变响度与脉冲发射率。其中响度更新中的α类似于退火因子,响度变化会影响算法的收敛速度。因此,我们考虑改变响度与脉冲发射率更新的条件。 文中提出的改进的二进制蝙蝠算法(ABBA)的伪代码如下: 算法2 改进的二进制蝙蝠算法: 1:设置最大迭代次数tmax, 频率的上界和下界Fmax和Fmin, 响度和脉冲发射频率的递减因子α和γ, 脉冲发射率的最终值r(0); 2:随机初始化蝙蝠种群的位置Xi(i=1,2,…,n), 速度Vi=0, 频率Fi, 脉冲发射率ri和响度Ai 3:while t 4: for i=1;i 5: 用式(1)与式(2)更新当前个体i的频率和速度 8: if (rand>ri) then 9: 在最佳解决方案中随机选择一个解决方案(Gbest) 10: 用Gbest改变位置向量的一些维度 11: end if 12: 利用随机飞行生成新解 14: 接受新的解决方案 15: 用式(5)和式(6)更新响度Ai和脉冲发射率ri 16: end if 17: end for 18: 给当前种群个体排序并选择出Gbest 19:end while 其中,改进部分用下划线标出。 为了评估提出算法的性能,将ABBA与7个最近提出的特征选择算法进行了对比实验,所用的对比算法均来自已发表的文献,具体信息见表1。 表1 最新特征选择算法的信息 将ABBA与BBA中的公共参数都设为相同的值,所有实验均采用包裹式方法较常用的KNN分类器,在来自UCI机器学习数据库的22个数据集上进行,见表2。 表2 数据集的特征数和实例数 续表2 ABBA是通过Python3.7和开放的工具包scikit-learn实现的,实验均在配置为Intel(R) Core(TM) i7-8550U CPU @1.80 Ghz 2.00 GHz的电脑上进行,实验结果均为采用五折交叉验证方法的25次独立实验的平均结果。 文中将分类准确率(ACC)和降维率(DR)作为算法性能的评价指标,公式为: (8) (9) 式中:NCC----正确分类的样本数量; NAS----总样本数量; NSF----选择特征的数量; NAF----所有特征的数量。 文中还采用适应度函数来评价所选特征子集,适应度函数的计算依赖于KNN分类器。 fitness(x)=α*×ACC+β*×DR, (10) 式中:α*,β*----参数。 文中将分类准确率作为主要优化目标,取α*=0.99,β*=0.01,使算法在提高分类准确率的同时尽量减小特征子集的长度。 在实验结果分析的过程中,采用标准差统计量来反映多次实验结果的变化情况,对于M次独立实验,统计标准差的计算方法为 (11) 式中:g*i----在第i次运行中的最佳解决方案; Mean----执行M次得到的平均解决方案。 实验数据包括ABBA与ABBA_1的对比,以及ABBA与MBAFS,HBBEPSO,PSO(4-2),MBO,BEPO_V4,SBOA这6个近期提出的特征选择算法的对比。这些特征选择算法是被广泛接受且表现良好的。其中ABBA_1在BBA中只应用了基于种群熵改进的传递函数,未加辅助改进。 实验结果包括所有算法的分类准确率数据表、维度缩减率数据表、统计标准差数据表和适应度收敛图像。 提出算法与对比算法的分类准确率见表 3。 表3 提出算法与对比算法的分类准确率 续表3 ABBA_1的分类准确率在18个数据集上优于BBA,其分类准确率的提高范围在0.08%~4.20%,在Leukemia,Breastcancer,PenglungEW, Tic-tac-toe这4个数据集上低于BBA,因为基于种群熵改进的传递函数在一定程度上增加了种群多样性,在算法后续演化不足的情况下,影响算法的收敛。因此,我们加入了辅助改进点。可以看到在增加辅助改进点之后,ABBA的分类精度相比ABBA_1进一步提高,ABBA在全部22个数据集上均优于BBA,其提高范围在0.312 5%~9.005%。加入辅助改进点后的ABBA相比ABBA_1在分类精度上提高0.216 5%~4.800 0%,在ABBA_1低于BBA的4个数据集上,加入辅助改进点后分类准确率均有提高。因此,辅助改进点的添加加速算法收敛,改善了因为种群多样性增加对算法收敛效果产生的影响。 文中提出算法与对比算法的降维率见表4。 表4 提出算法与对比算法的降维率 续表4 结合ABBA与6个最新特征选择算法的分类准确率数据来看,ABBA在17个数据集上优于所有的对比算法,在未取得最优的5个数据集中,spectew,BreastEW,glass这3个数据集上ABBA的分类准确率只低于6个对比算法中的一个。因此,在分类准确率方面,ABBA取得了较好的效果,在对比算法中很有竞争力。 在降维率方面,ABBA相比BBA有所下降,因为在设计特征子集的评价标准时,分类准确率的占比为0.99,而降维率的占比为0.01 。因此分类准确率是算法主要的优化目标,在分类准确率提高的同时降维率降低,是因为算法更趋向于选择对分类准确率贡献更高的特征子集,而不是更短的特征子集。ABBA的降维率在6个最新特征选择算法中不具有明显优势,但是在大多数数据集上,ABBA处于所有算法的平均水平上,并且在21个数据集上,ABBA的降维率并非所有算法中的最低值。 提出算法与对比算法的适应度标准差见表5。 表5 提出算法与对比算法的适应度标准差 相比于BBA的稳定性,ABBA在22个数据集上都有提升,其中在Exactly和vehicle两个数据集上提升最为显著,几乎在所有的数据集上ABBA的统计量标准差相比于BBA都提高了一个数量级。因此,ABBA的稳定性优于BBA。结合6个最新特征选择算法的统计量标准差数据来看,ABBA在7个数据集上取得最小值,只在ionosphere,glass,PenglungEW, Sonar这4个数据集上相比最小值相差一个数量级,其余未取得最小值的数据集上,ABBA均与最小值相差不大。 综上所述,ABBA在分类精度上取得了明显的提高,改善了BBA种群多样性下降快,易陷入局部最优的问题,赋予算法跳出停滞的能力。并且两个改进相互辅助,共同提高了算法的分类准确率。在最新的6个特征选择算法中,ABBA在分类准确率、鲁棒性、收敛特性方面具有明显优势。因此,ABBA是一种分类精度高、鲁棒性好的特征选择算法。 提出改进的二进制蝙蝠算法(ABBA)运用基于种群熵的传递函数改进,以及一个辅助改进点缓解了算法易早熟,陷入局部最优的问题。基于种群熵的传递函数可以适应算法收敛过程,在一定程度上增加种群多样性,并赋予算法克服停滞的能力。针对新的传递函数可能影响算法收敛这一问题,增加了辅助改进,改变了响度和脉冲发射率更新的条件,加速算法收敛。实验表明,辅助改进与新传递函数良好结合,可以共同提高算法的分类精度和鲁棒性,并且保证算法拥有较好的收敛性能。在与最新的特征选择算法的对比中,ABBA在主要优化目标上具有明显优势,是一种有竞争力的特征选择算法。 下一步研究计划中考虑使用其他方法代替辅助改进,在不改变原有搜索机制下增加算法的演化能力,加快算法收敛,与传递函数相互辅助,进一步提高算法的分类准确率与降维率。2 改进的二进制蝙蝠算法
2.1 运用种群熵对传递函数的改进


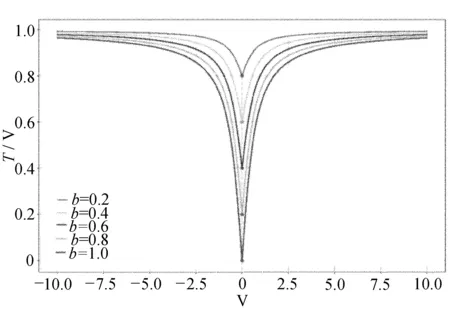
2.2 辅助改进
3 实验及其结果分析
3.1 实验设计



3.2 评价准则

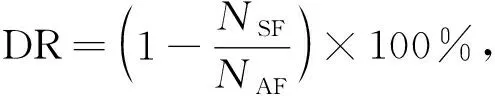
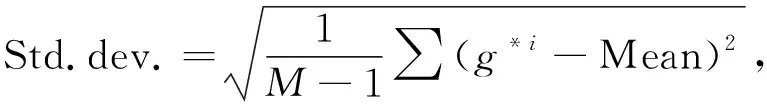
3.3 实验结果及分析
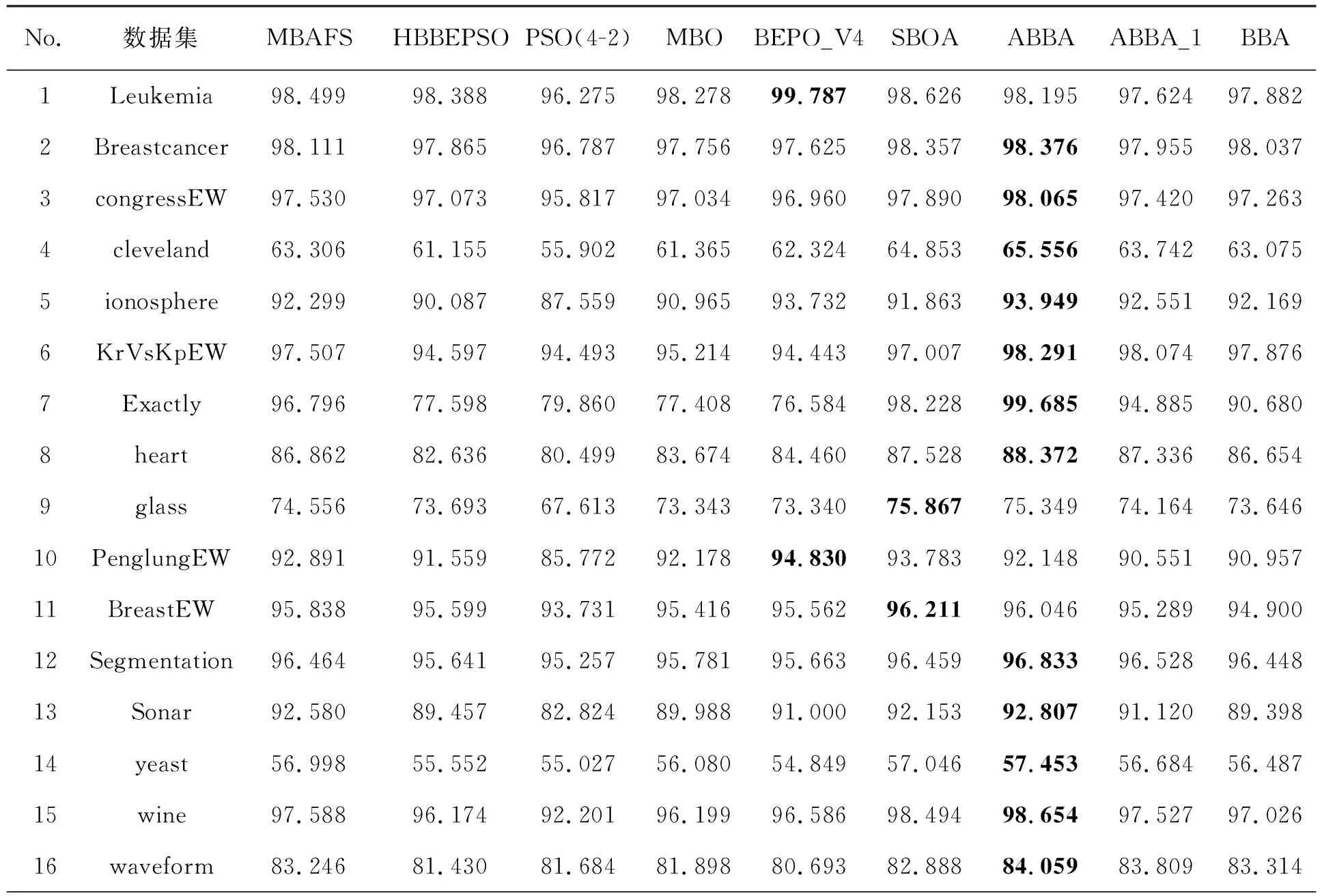




4 结 语

