改进环形耦合结构多电机协同控制

顾 昕， 王宏志， 胡黄水

(长春工业大学 计算机科学与工程学院， 吉林 长春 130102)

0 引 言

随着工业发展，自动化程度稳步提升，多电机协同控制系统已经被大范围应用到焊接、流水生产线、电梯系统、机器人控制等各个领域。多电机协同控制系统性能的好坏直接影响产品质量以及生产效率。采用传统的电机协同控制方式已经无法满足高性能协同控制的要求,因此,研究多电机协同控制具有良好的发展前景,深受各界关注[1]。无刷直流电机(Brushless DC Motors, BLDCM)具有效率高、过载能力强、使用寿命长、体积小、功率密度高等优点[2]，使其在多电机协同系统中被广泛应用，设计出稳定性高的多无刷直流电机协同控制系统具有重要意义。

目前，多电机控制系统主要包括主从控制结构、并行控制结构、交叉耦合控制结构、相邻交叉耦合控制结构、偏差耦合控制结构、环形耦合控制结构等[3]。主从控制结构是将多电机系统中的某个电机当成主电机，其他电机则为从电机，将主电机的信号作为参考，从电机去跟踪该信号，当主电机发生突变时，会很大程度上影响到整个多电机系统的精度问题。并行控制结构中，多电机系统给定参考速度，将这一输入速度信号送达给不用电机。在这个控制结构中，各个电机相互不受影响[4]。该控制系统的优点是每台电机的输入转速均为给定参考速度，保持一致，且同步误差小。由于每台电机相互独立，系统之间没有耦合，在某一电机接收到扰动信号或负载发生变化时，该多电机系统的其他电机则无法获取相应信号，并行控制结构系统不能自调整运行，受干扰影响较大。交叉耦合控制结构把计算电机之间的位置与速度的误差值当作反馈信号传送到这个多电机系统的每个电机的输入端口，通过这一反馈控制来保证这个多于两个电机的多电机系统上具有良好的效果，若是在三个及三个以上电机的多电机系统上，这一控制结构并不能取得很好的反馈效果。为了满足交叉耦合控制结构可用于三个及三个以上的多电机系统上，提出了相邻交叉耦合控制结构。偏差耦合控制结构对交叉耦合控制在多电机场景下的优化，将反馈信号改为由这个多电机系统上的所有电机的运行状态共同来决定，大大提高了系统的耦合程度，但是在负载突变的时候，其系统复杂性较高，由于其波动影响会导致此系统的不稳定性增加。环形耦合控制结构的反馈机制是只做每两个电机之间的误差补偿，在增加电机个数的情况下，不会增加多电机系统的复杂性，不过同时性略差，误差反馈会出现迟滞的问题。

在实际情况中，多电机控制系统的运用环境各有不同。在机械臂的运动过程中，比如做抓取、焊接等其他动作时，每个电机由于位置与力矩等原因，若做到同步与同速，机械臂会出现抖动问题，这与在传送带上运用多电机同步控制系统等其他情况不同。针对此问题，文中建立一种基于模糊PID的环形耦合控制算法模型，对其角度与位移进行仿真，并对仿真结果进行比较与分析。

1 环形耦合控制结构

环形耦合控制结构相对于其他控制结构的区别是在考虑每台电机的实时转速和额定转速之间的误差同时，只做每两个电机之间的误差补偿。环形耦合控制策略中所有电机对同一给定的参考信号实现一致跟随,而且电机间两两实现同步误差耦合补偿,所以系统起动过程的跟随性能和抗干扰性能够得到保证[5]。

同步误差的反馈和补偿也只在相邻的两台电机之间进行，即使是由大量电机构成的多电机协同控制系统，控制结构也不会过于复杂，因此更适用于多受控电机的多电机协同控制系统，目前是一种较为理想的多电机协同控制策略。

由三台无刷直流电机构成的多电机系统的环形耦合环如图1所示。

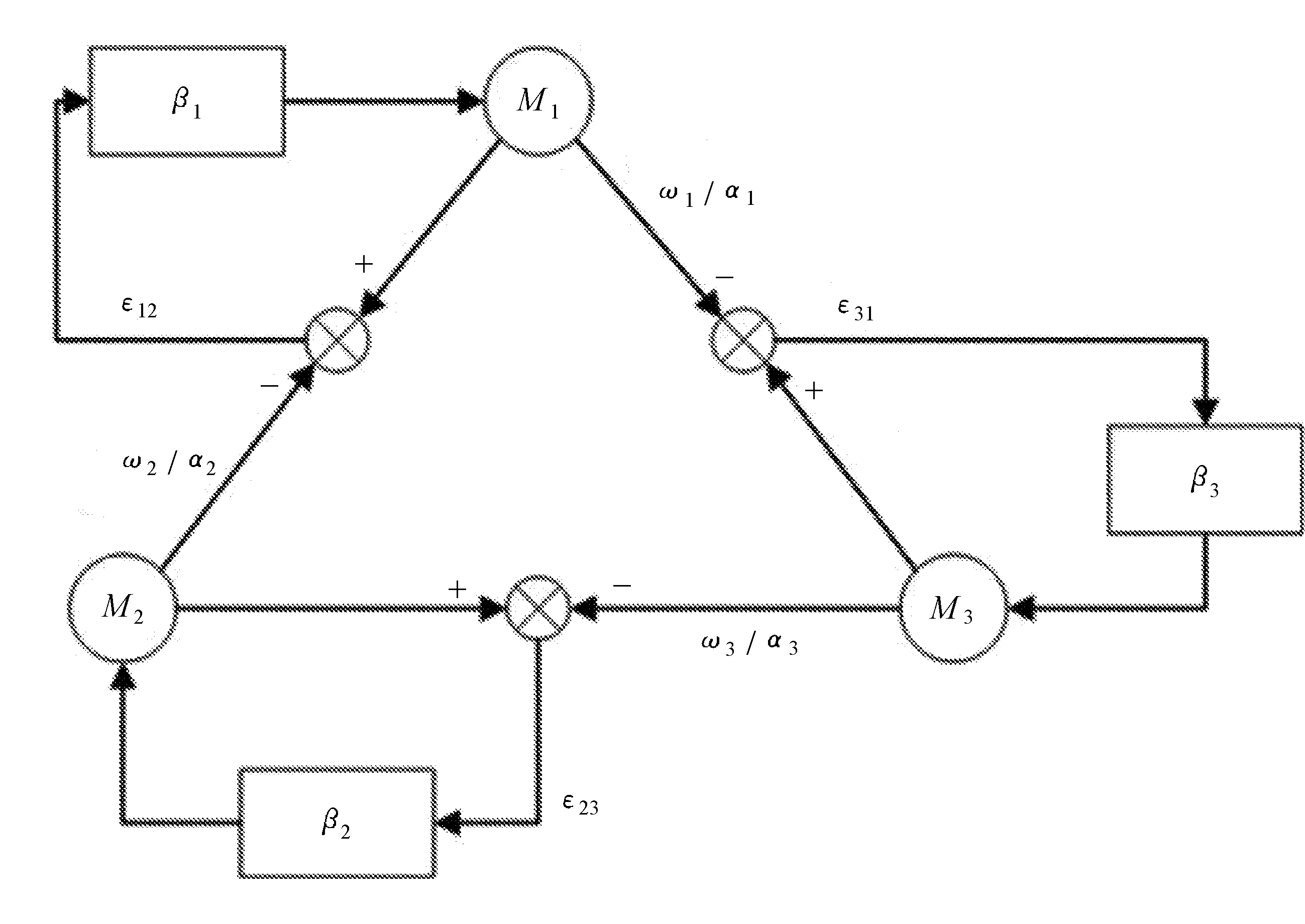
图1 三电机环形耦合环

由图1可以看出，以电机M1为例，电机M1和M2这两个电机的同步误差ε12反馈给电机M1。下两个电机之间的反馈以此类推，所有电机之间两两耦合，这样就形成了一个三电机的耦合反馈控制环。

校长作为教育的办学实践者，必须有教育的情怀与激情。人是为了追求幸福才来到世界上，教育者身上寄托了人们太多的精神梦想，我们以梦想的名义仰望幸福。当校长有着坚定不移的职业精神，拥有宁静的心灵，才能全心地去关爱每一个学生，才能真正地去敬畏每一个生命，才能“不抛弃，不放弃”。

由环形耦合环得到多电机环形耦合控制结构如图2所示。

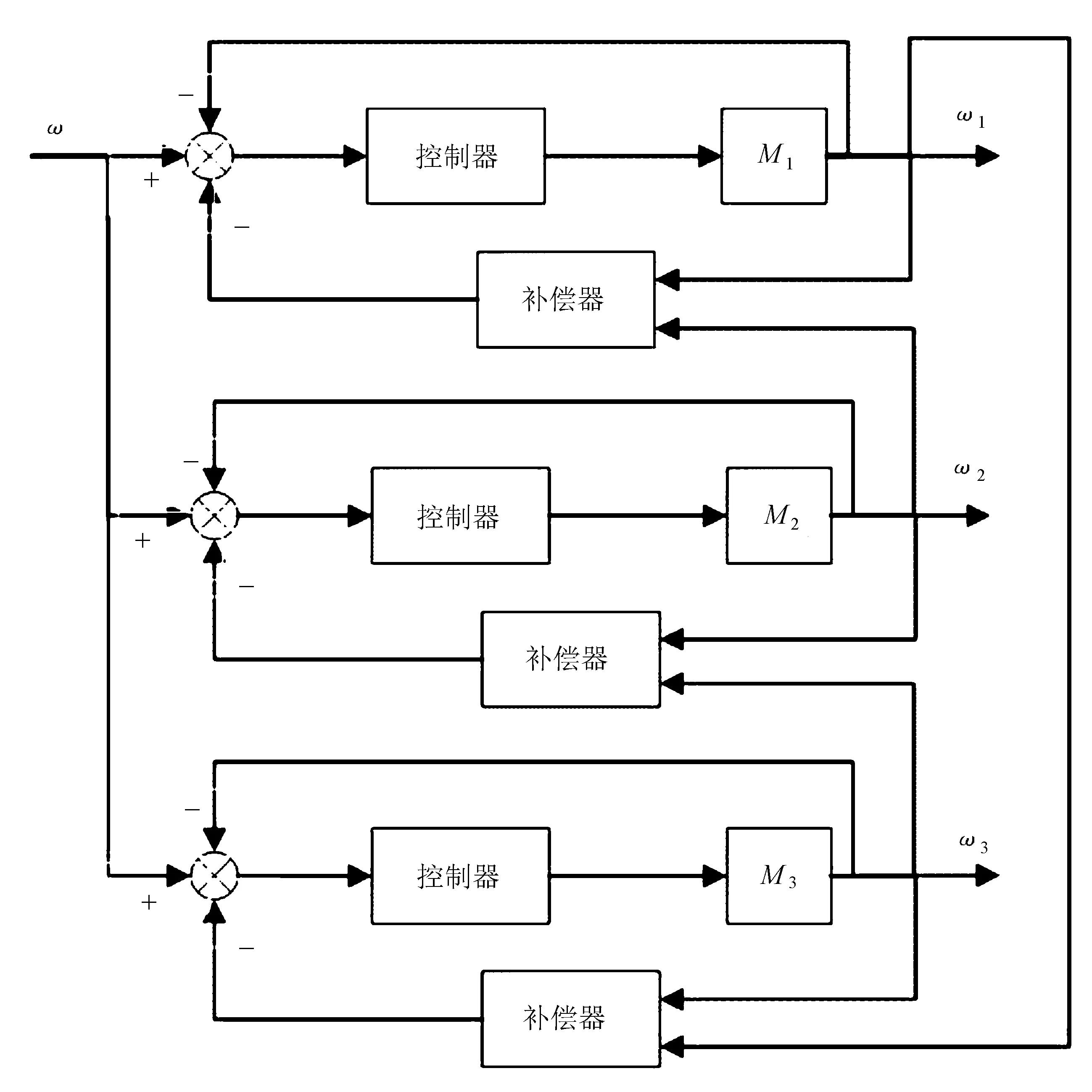
图2 多电机环形耦合控制结构原理图

由图2可知，多电机同步控制系统主要由电机驱动系统、同步误差补偿器和控制器三部分构成。在补偿模块的影响下，使用环形耦合控制策略,将产生的误差信息传递给对应的电机，多电机同步驱动器也会收到相同的信号。采用转速耦合进行补偿，然后将信号传递给控制器，对提高系统一致性和稳定性有很好的效果[6]，扰动、负载等外力对电机转速带来的影响会逐渐减小。

设第i(i=1,2,3)台电机的转速跟踪误差为

ei=ω-ωi,

(1)

式中:ω----系统各电机给定转速值。

设第i台电机与第i+1台电机的同步误差为

εi=ωi-ωi+1。

(2)

通过环形耦合速度补偿器校正的第i台电机的跟踪误差为

Ei=ei-Kiεi,

(3)

式中:Ki----第i台电机的补偿系数。

2 改进环形耦合控制结构

由于传统的环形耦合控制结构同时性差，误差反馈会出现迟滞的问题。在原有的结构上进行改进，提出速度补偿器的设计理念，在速度补偿器中加入动态因子，设计出满足以上要求的改进型环形耦合控制结构。并针对多电机系统同步误差较大的问题设计了速度补偿器[7]。

设ωave为n台电机的平均转速，其值为

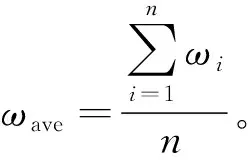
(4)

优化后的第i台电机的速度补偿器结构如图3所示。

传统的速度补偿器是用第i台电机转速与相邻两个电机转速做差再进行求和，经过补偿比例系数，输出量εi,即为速度补偿。

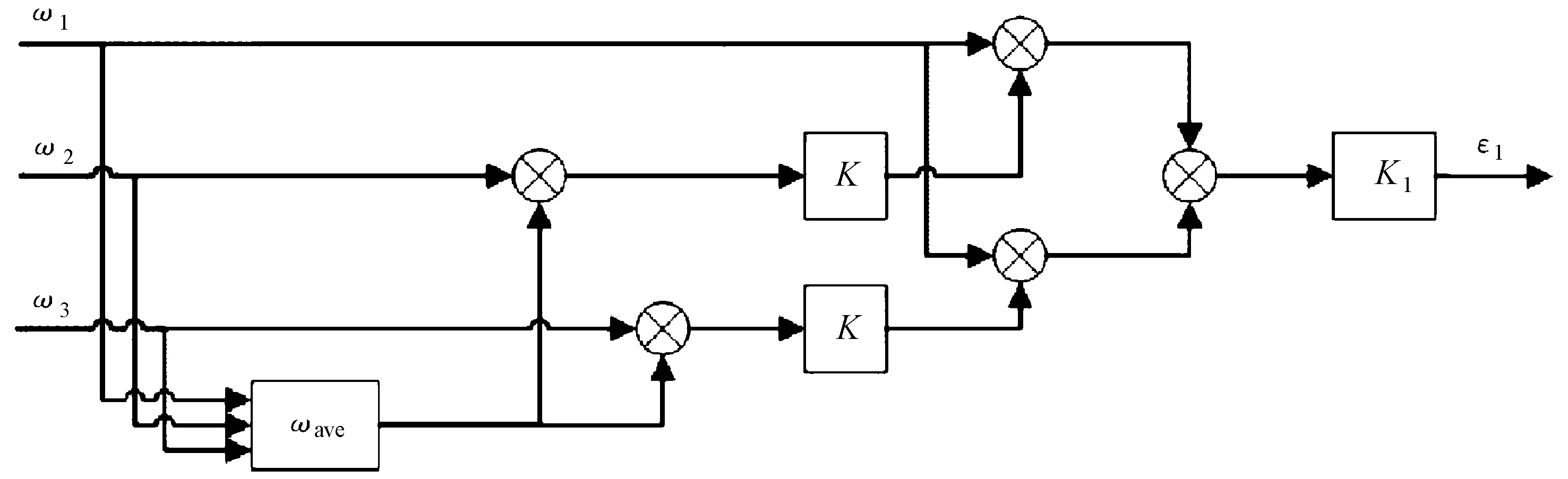
图3 优化速度补偿器结构图

优化后的速度补偿器采用相邻的两个电机转速分别与多个电机的实时转速的平均值做均值，即图3中K=0.5，然后再与第i台电机的转速做差，补偿比例系数为满足实时性，其比例系数为

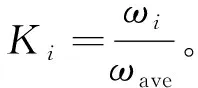
(5)

3 模糊PID控制器

在环形耦合控制结构控制器中使用模糊PID控制算法[8]，模糊规则的输入量为偏差e和偏差变化率ec，PID控制参数的比例系数ΔKP、积分系数ΔKI、微分系数ΔKD，输出量由于速度误差随系统由初始状态向稳态大范围变换，并伴有同步误差，因此模糊逻辑控制中的输入变量域根据速度误差范围进行调整，偏差e和偏差变化率ec在模糊集上的论域为:

e=[-2,2],

ec=[-1,1]。

输入变量的隶属度函数在三角函数域中采用等比例分布，如图4所示。

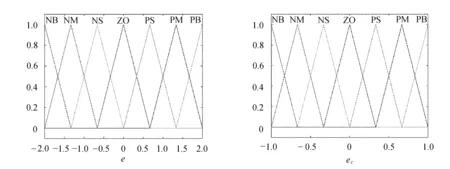
(a) 输入变量e (b) 输入变量ec

输出变量在模糊集论域为:

KP=[0,5],

KI=[0,1],

KD=[0,3]。

输出变量的隶属度函数如图5所示。

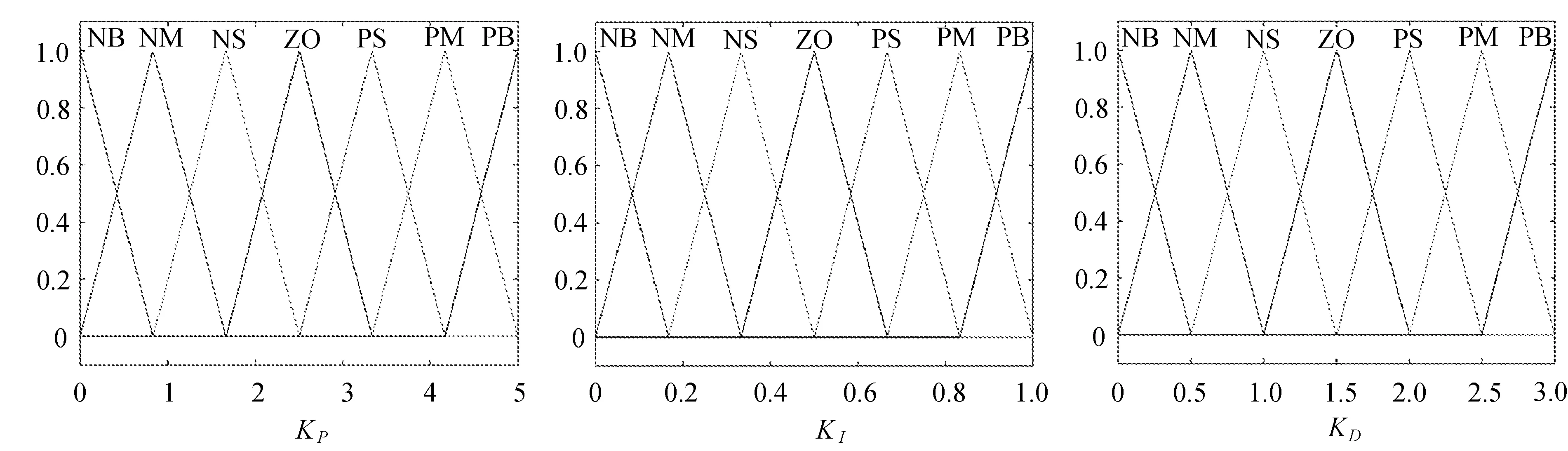
(a) 输出变量KP (b) 输出变量KI (c) 输出变量KD

输出变量与输入变量曲面关系如图6所示。

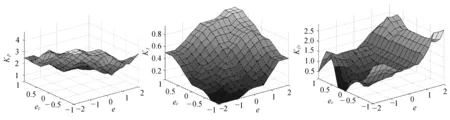
(a) KP (b) KI (c) KD

输入输出变量的模糊语言集为{NB、NM、NS、ZO、PS、PM、PB} ={“负大”“负中”“负小”“零”“正小”“正中”“正大”}[9]，模糊规则包含49条比例系数KP，49条积分系数KI，49条微分系数KD，共计147条模糊规则。具体模糊规则分别见表1～表3。

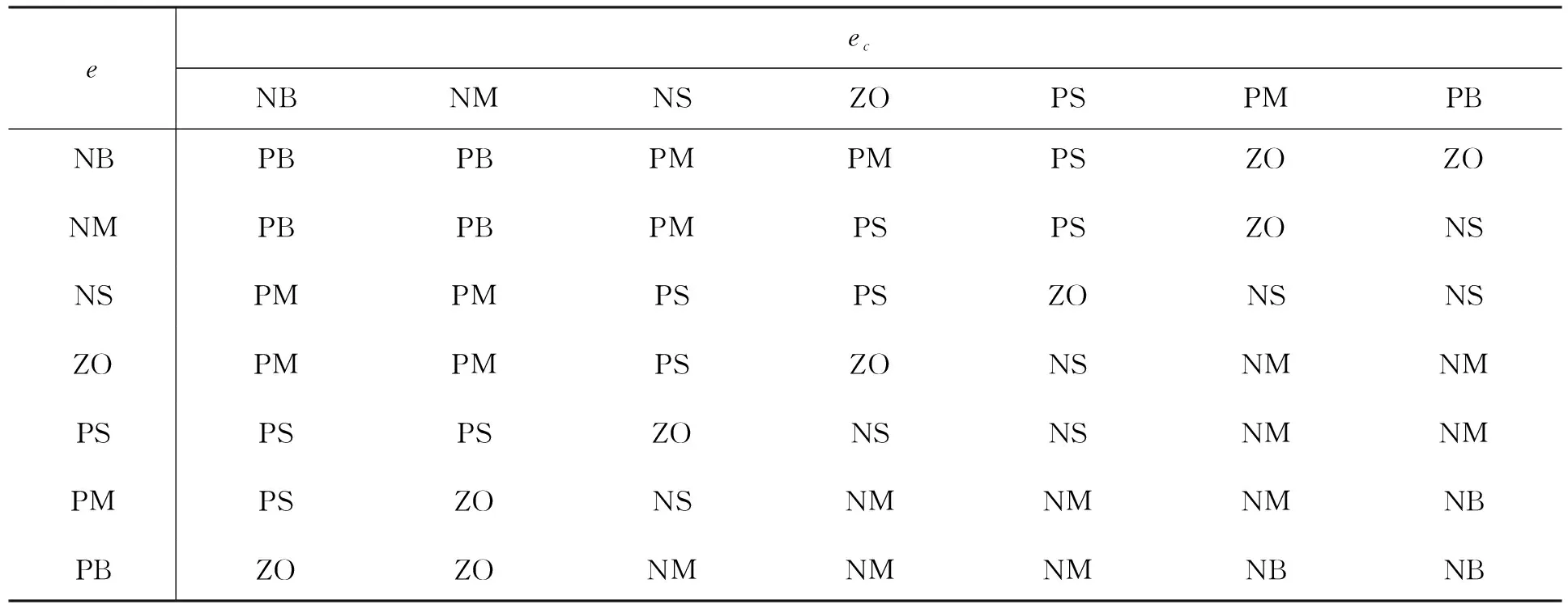
表1 ΔKP的模糊控制规则

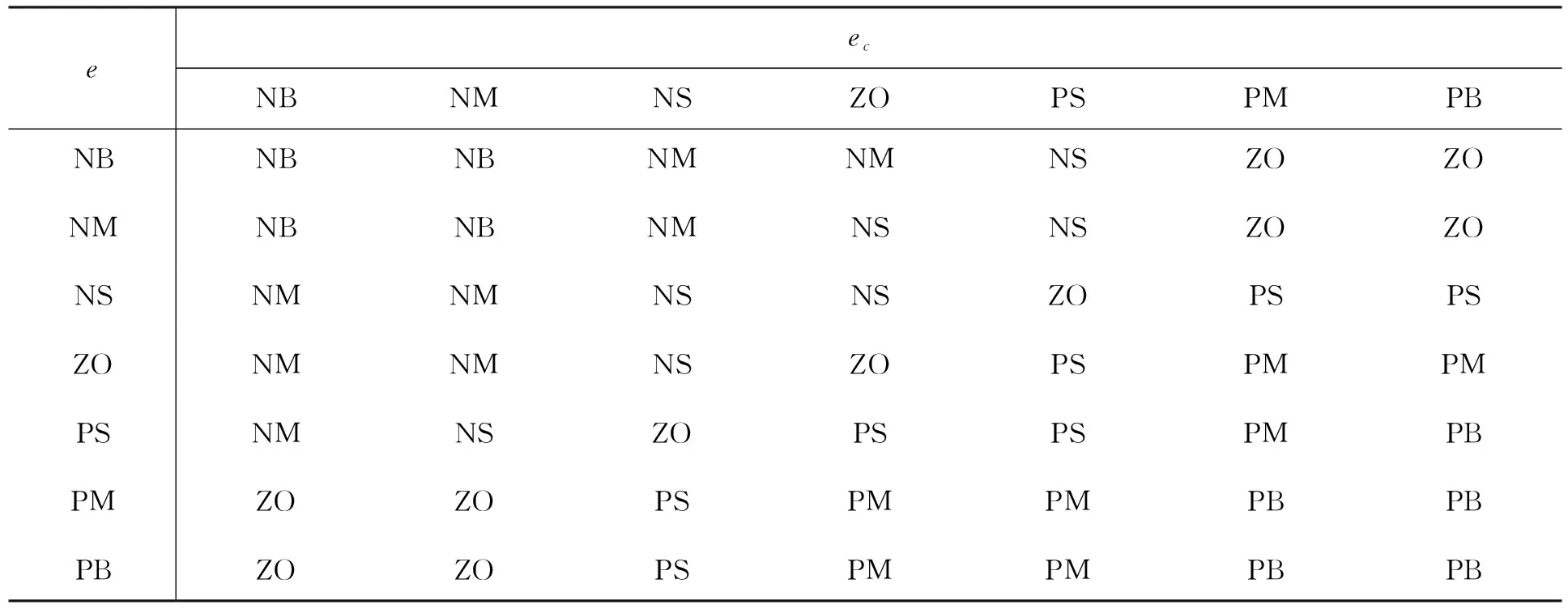
表2 ΔKI的模糊控制规则

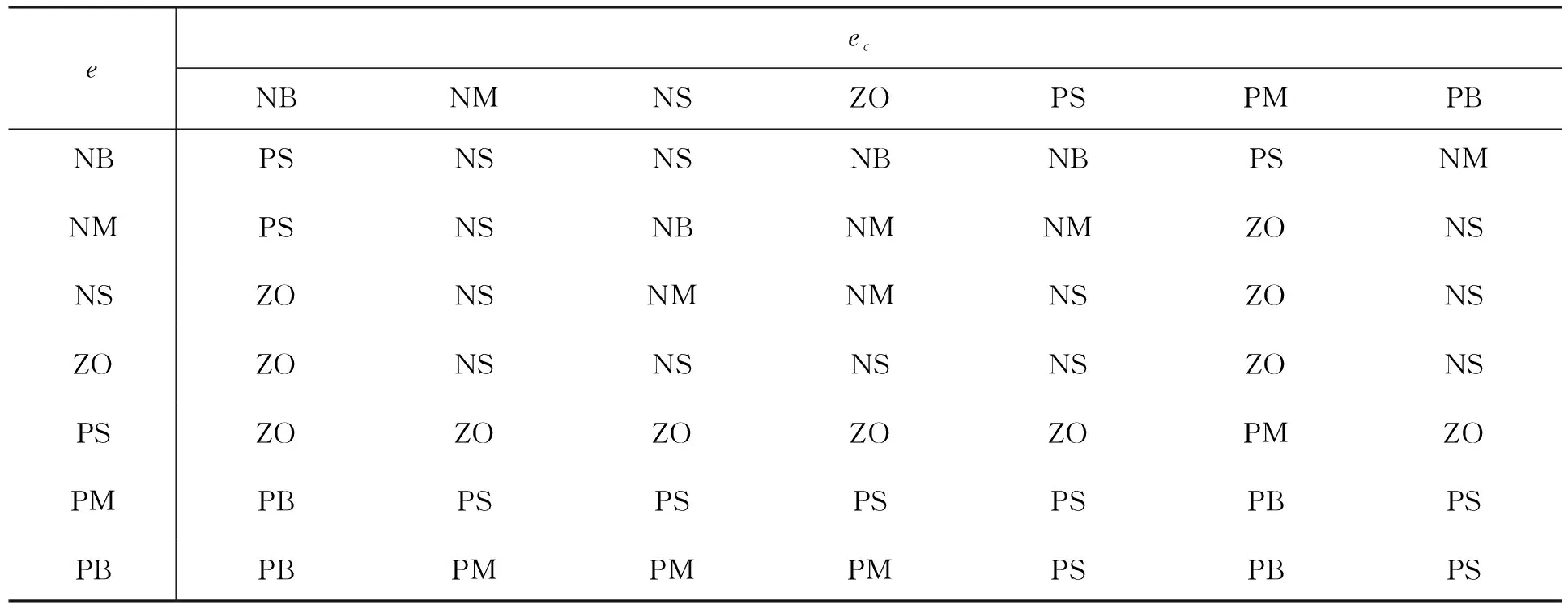
表3 ΔKD的模糊控制规则

4 仿真分析

在Matlab/Simulink环境下，搭建以三台无刷直流电机构造的环形耦合控制系统模型[10]。对文中提出的基于模糊PID的改进环形耦合控制方法进行仿真研究。

由于是协同控制而非同步控制，实际中，三台电机由于位置等其他问题，转速等其他参数会有区别。在仿真中为了可以更加明显地看出三个电机的不同负载启动和突加负载时的实时性，三台无刷直流电机BLDCM的给定转速均为1 000 r/min，仿真运行时间t=0.5 s。

启动阶段，令M1空载、M2接2 N·m负载，M3接8 N·m负载，未改进环形耦合控制结构启动转速如图7所示。

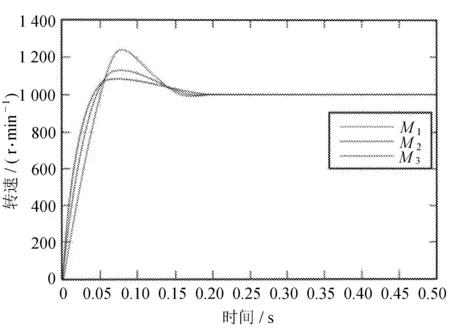
图7 未改进环形耦合控制结构启动转速

改进后的环形耦合控制结构启动转速如图8所示。

对图7与图8进行比对分析，相较于传统的环形耦合控制结构，改进型控制结构的三台无刷直流电机的调节时间变动幅度较小。在电机起动瞬间，改进型环形控制结构的同步误差最大值和同步误差调节时间相较于传统的环形耦合控制结构有明显减小[11]。

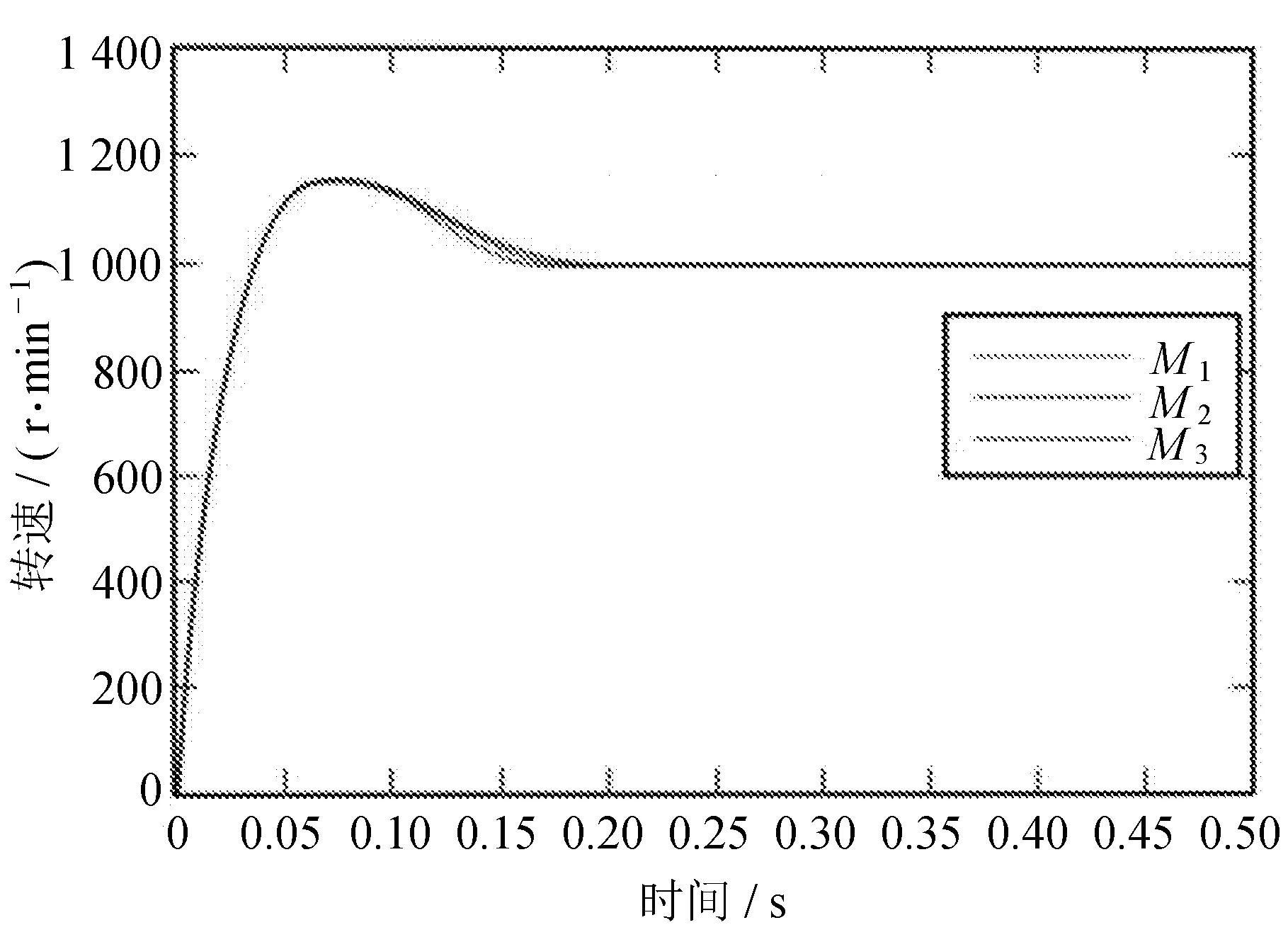
图8 改进环形耦合控制结构启动转速

当三个电机稳态运行时，在0.2 s时，对电机M2突加负载4 N·m，对电机M3突加负载10 N·m，未改进环形耦合控制结构突加负载转速如图9所示。

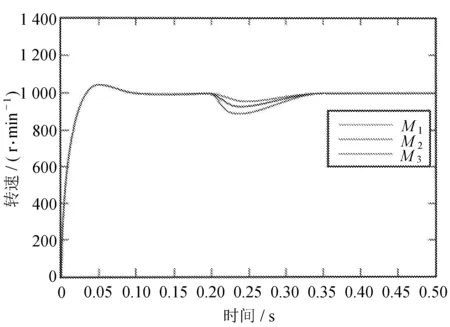
图9 未改进环形耦合控制结构突加负载转速

改进后的环形耦合控制结构突加负载转速如图10所示。

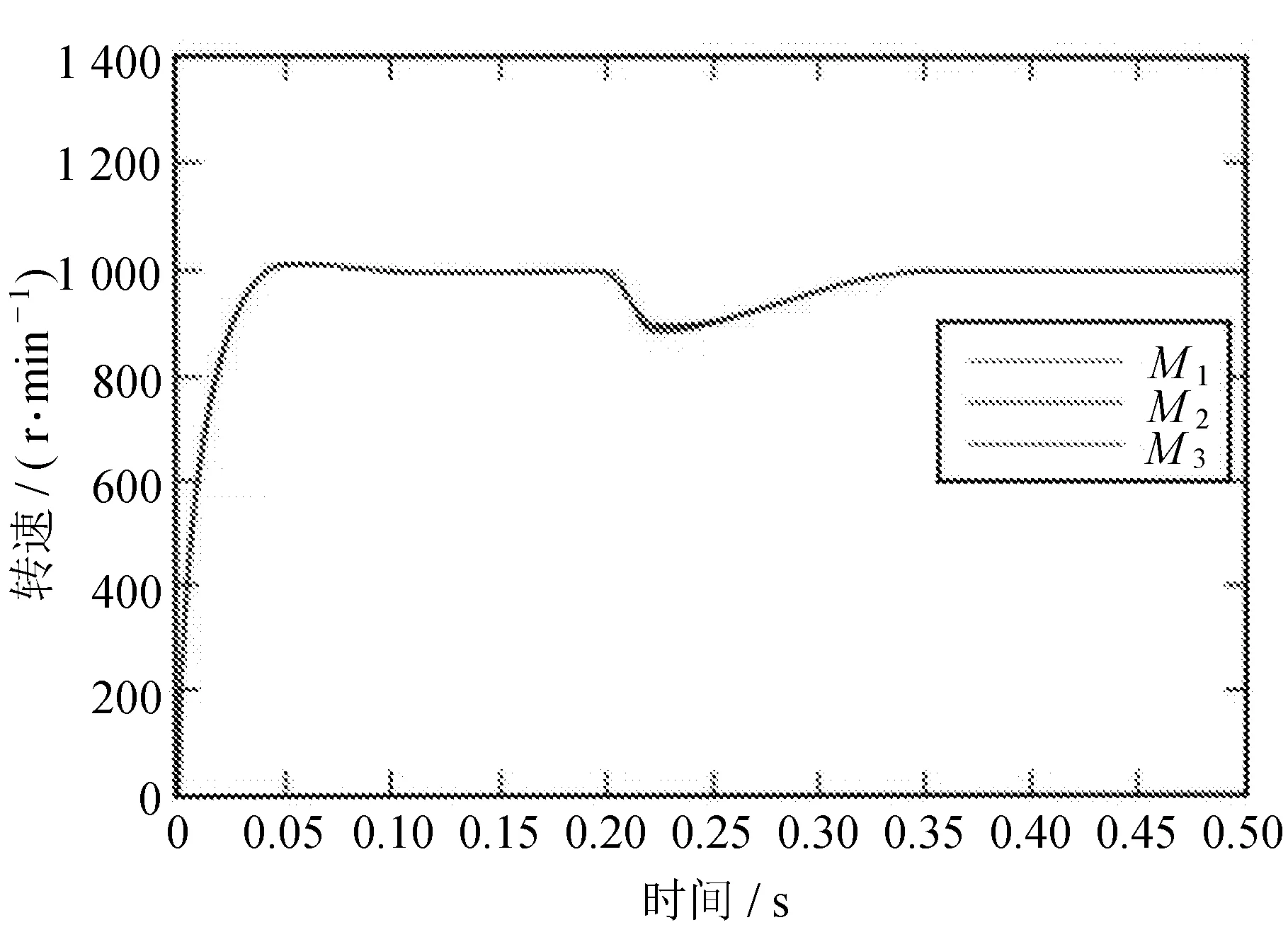
图10 改进环形耦合控制结构突加负载转速

通过两个仿真图比对分析，改进环形耦合控制结构的转速调节时间与环形耦合控制结构基本一致。对电机M2和M3突加不同的负载时，电机M1的转速误差相比传统环形耦合控制结构有所增加，电机M2的转速误差变化较小，电机M3所受负载最大，其转速误差相对比于传统环形耦合控制结构有明显减小，三个电机的转速基本保持一致。改进型控制结构的同步误差最大值比传统控制结构明显下降；在速度补偿器中加入了实时的动态因子[12]，改进型环形耦合控制结构的同步误差调节时间缩小。

5 结 语

在环形耦合控制结构的基础上进行改进，使用模糊PID算法优化电机控制器，提高多电机协同控制系统的性能[13]。基于Matlab/Simulink环境下，对改进前后的环形耦合控制结构的启动阶段和突加负载情况进行对比分析，结果表明，改进后的环形耦合控制算法具有更小的稳态误差及较强的鲁棒性。