基于机器学习原理的函数定阶法对乙醇偶合制备C4烯烃问题的分析

邱予骁,杨莉军,邓茹荟,张垚霖

(北京印刷学院,北京 102600)

1 问题的发现

催化剂是一种改变反应速率但不改变反应总标准吉布斯自由能的物质,在用乙醇催化偶合制备C4烯烃的过程中,催化剂会以降低反应所需活化能的方式改变乙醇的转化率和C4烯烃的选择性。因此催化剂的组成不同,用乙醇制备C4烯烃的工艺条件不同。为了研究出制备C4烯烃最佳的催化剂组合和温度,首先要探究不同催化剂组合对乙醇转化率及C4烯烃选择性的影响。因此可以利用控制变量法分组研究,每组做出相应的乙醇转化率随温度变化曲线和C4烯烃选择性随温度变化曲线并进行对比,最终得出结论:在催化剂组合为200mg 1wt% Co/SiO2-200mg HAP-乙醇浓度0.9mL/min时效果较好。而实际生产生活中催化剂对温度极为敏感,每种化学反应的反应温度都被严格控制在一个固定区间。针对“温度对C4烯烃转化率的影响”这一问题,仅凭直觉确定温度-转化率函数的拟合阶数显然是不准确的,在实际生产生活中也并不可取。[1]因此为了深入确定拟合曲线的具体参数,就要确认拟合时所用曲线的阶数,首先对原始数据(表1)进行初步拟合分析。

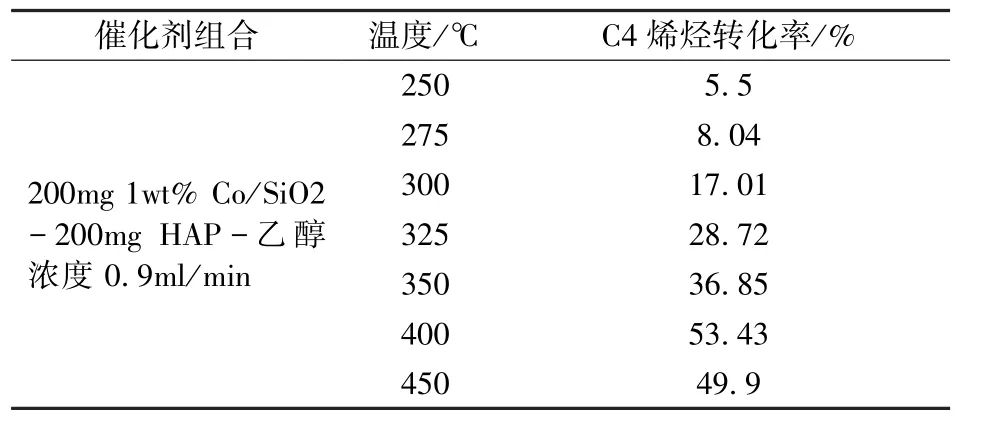
表1 原始数据

通过分析可知:一阶函数拟合(图1)效果最差;四阶函数(图4)虽然拟合效果最好,但与三阶函数拟合(图3)效果相差甚微,且容易引起过拟合,增加了实际生产过程中的复杂度。

因此,经过初步分析可以排除一阶导数拟合和四阶导数拟合。

2 基于机器学习原理对函数定阶

为了确定最终是用二阶拟合还是三阶拟合,根据机器学习原理,[1-3]将np.polyfit(x,y,2),np.polyfit(x,y,3)视为两个学习机,用统计假设检验的方法,分别计算出两个学习机在对给定样本模拟中的测试错误率从而推出两个学习机的泛化错误率,通过比较其泛化错误率来确定学习机的优劣,从而确定温度对C4烯烃转化率的影响采用二阶拟合还是三阶拟合。[4-7]

设二阶模拟对应的测试错误率为∊2,三阶模拟对应的测试错误率为∊3。首先选取样本点个数最多的A3组对两个学习机进行检验,结果如图5、图6所示。[8]

通过拟合,可以得到预测值与样本点差值的集合。在实际生产生活中,人们往往难以接受误差值较大的模拟,这会给生产带来极大的不确定性。这里引入均方误差MSE:

yi为真实样本值,^yi为预测值,m为样本点个数。最 终 求 得MSE2=26.178627,MSE3=9.873714。随后,计算每种学习机的决定系数R2,其中R2的定义为

yi是实际值,fi是预测值,是实际值的平均值。FVU为fraction of variance unexplained,RSS为Residual sum of squares,TSS为Total sum of squares。

一般地,R2越接近1,表示回归分析中自变量对因变量的解释越好[5-6]。最终求得=0.9663,=0.9873。

结合MSE2与MSE3的对照,可见三阶函数的拟合效果更加理想。对于二阶拟合曲线,将误差值明显较大的第四次、第六次、第七次模拟称为误判。对于三阶拟合曲线,将误差值明显较大的第五次模拟以及第六次模拟称为误判。由此可得学习机np.polyfit(x,y,2)的测试错误率∊2=3/7=42.86%,np.polyfit(x,y,3)的测试错误率∊3=2/7=28.57%。

泛化错误率为∊′的学习机在一个样本上犯错的概率是∊,测试错误率E意味着在m个测试样本中恰有E×m个被误分类。假定测试样本是从样本总体分布中独立采样而得,那么泛化错误率为∊′的学习机将其中m′个样本误分类、其余样本全都分类正确的概率为

由此可估算出其恰将^∊×m个样本误分类的概率如式(4),这也表达了在包含m个样本的测试集上,泛化错误率为∊′的学习器被测得测试错误率为^∊的概率为

已知学习机np.polyfit(x,y,2),np.polyfit(x,y,3)的测试错误率,则解式(5)

可知,P(^∊;∊′)在∊′=^∊是最大,|∊′-^∊|增大时P(^∊;∊)减小。这符合二项(binomial)分布,对于学习机np.polyfit(x,y,2),其测试错误率∊=42.86%,则7个样本中测得3个被误分类的概率最大。对于学习机np.polyfit(x,y,3),其测试错误率∊=0.2857,则7个样本中测得2个被误分类的概率最大。

图7是程序模拟学习机np.polyfit(x,y,2)二项分布的结果图,图8是程序模拟学习机np.polyfit(x,y,3)二项分布的结果图:

综上,最终确定以三阶函数Y=ax3+bx2+cx+d作为样本拟合的通用函数模型。

3 函数检验

可用“二项检验”(binomial test)来对“∊≤0.3”(即“泛化错误率是否不大于0.3”)这样的假设进行检验。

更一般地,考虑假设“∊≤∊0”,则在1-α的概率内所能观测到的最大错误率如式6计算。这里1-α反映了结论的“置信度”(confidence)。

此时若测试错误率^∊小于临界值¯∊,则根据二项检验可得出结论:在α的显著度下,假设“∊≤∊0”不能被拒绝,即能以1-α的置信度认为,学习器的泛化错误率不大于∊0;否则该假设可被拒绝,即在α的显著度下可认为学习器的泛化错误率大于∊0。

我们也可以将所有的催化剂组合对应的样本数据对学习机进行多次测试,这样会得到多个测试错误率,此时可使用“t检验”(t-test)。针对本题,我们可以得到了k个测试错误率,其中k=21,^∊1,^∊1,…^∊k(k=0,1,2,3…,20,21),则平均测试错误率μ和方差σ2为:

考虑到这21个测试错误率可看作泛化错误率∊0的独立采样,则变量

服从自由度为k-1=20的t分布。对假设“μ=∊0”和显著度α,我们可计算出当测试错误率均值为∊0时,在1-α概率内能观测到的最大错误率。

4 结语

该模型能充分说明三阶函数拟合的优点,且三阶函数模型在题目给定的温度区间内有着极好的稳定性,决定系数R2极接近1。同时学习机np.polyfit(x,y,3)二项分布的结果图相比np.polyfit(x,y,2)二项分布的结果图整体更靠近y轴,说明三阶拟合函数对样本趋势的预测更加准确。但该模型需要大量样本进行测试,对样本数量较少的催化剂组合的预测不能充分发挥该模型的优势。