基于偏微分方程的双币种扩展期权定价
何家文
南宁学院通识教育学院 广西南宁 530200
1 概述
扩展期权是允许发行者或期权持有者扩展其初始合约的到期日,当期权持有者扩展其合约到期日时,相应的执行价格要被调整,同时持有者必须向期权出售者支付一定的额外溢酬。扩展期权的最大特点就在于期权持有者在期权初始到期日时为达到利益最大化可以选择执行或放弃该合约,还可以延长该合约的期限。Longstaff[1]在经典的市场模型[2]下研究扩展期权定价问题。Gukhal[3]采用股价满足Merton跳扩散模型[4]对扩展期权进行定价,彭斌[5]以标的资产遵循跳分形过程为基础,推导扩展期权价格的封闭解,Chung等[6]研究一类多期扩展期权定价问题,邓国和[7]在随机波动率混合跳跃仿射扩散模型下研究扩展期权定价。
本文讨论了双币种扩展期权,双币种期权是为投资者在本国购买国外标的资产而设计的一种期权,受到国内和国外两个不同货币市场影响。该类期权可规避在贸易中遇到的汇率风险。双币种扩展期权的收益函数是汇率与国外标的资产组合而成,且其到期日可延长,因此可以方便投资者进行投资和对冲风险。目前关于双币种期权研究[8-15]较多,取得一系列的研究成果,而关于双币种扩展期权的研究较少,文献[16]在跳扩散模型下研究双币种扩展期权定价问题。本文利用偏微分方程的方法在随机波动率过程下讨论了双币种扩展期权的定价问题,在本文考虑的期权收益支付形式是执行价格以国内货币计价。
2 模型假设
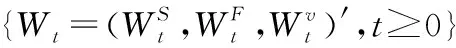

(1)
这里rf为国外利率,rd为国内利率,σS、σF为非负常数,α、θ、σV分别是随机波动率运动方程中的均值回复速度参数,长期均值参数,波动率参数,且2αθ-σ2≥0。
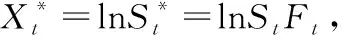
(2)
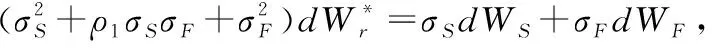
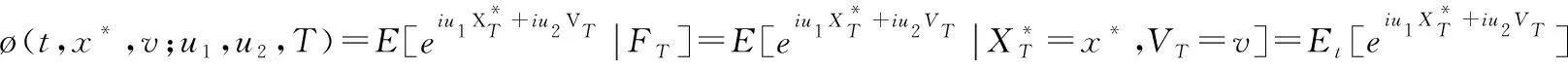
ø(t,x*,v;u1,u2,T)=exp{iu1x*+B(τ,u1,u2)v+C(τ,u1,u2)}
(3)
其中
(4)
(5)

(6)
由于市场模型(1)具有仿射结构特征,故(6)的解ø(t,x*,v;u,1,u2,T)具有指数形式的解结构为:
exp{iu1x*+B(t,u1,u2)v+C(t,u1,u2)}
(7)
将(7)带入方程(6),则待定系数B(t)=B(t,u1,u2),C(t)=C(t,u1,u2)满足:
(8)
(9)
求解上述微分方程(8)、(9)得解为(4)、(5)式。
3 双币种扩展期权定价
考虑一类执行价格以国内货币计价的双币种看涨期权定价,对于其他三类双币种扩展期权可类似获得。该类型的双币种欧式期权在到期为T1,执行价格为K的收益函数为max{0,ST1FT1-K},其扩展期权是允许持有人将初始的到期日T1扩展至T(T>T1),同时要给期权的发现者支付一定的额外费用δ,而执行价格也会被调整到K1,此时双币种扩展期权在到期日为T1时的收益函数为V(S,F,K,K1,T1,T)=max{0,ST1FT1-K1,CE(T1,S,F,v,K,T)-δ},这里C(T1,S,F,v,K,T)是执行价格和到期日为K,T的双币种欧式看涨期权在T1时刻的价格。
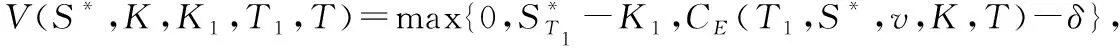
有当S*∈(U,+∞)或S*∈(0,L)时,期权不被扩展;当S*∈(L,U)时,期权被扩展。
由于扩展期权有两个到期日T1和T,故需计算国外货币下公司资产对数价格X*在两个不同时点上的联合特征函数ø(u1,u2,T1,T),设T1≤t 定理 设在市场模型(1)下,双币种扩展看涨期权在t时刻的价格为: (10) 根据二维的Fourier逆变换有: 这里 I3类似I2的计算,定理证毕。 显然,当Vt为常数时,公式(10)为B-S模型下双币种扩展期权定价公式。 本文在汇率和标的资产的对数价格满足随机波动率条件下,研究双币种扩展看涨期权的定价问题,通过测度变换及Fourier逆变换等方法得到其定价公式。该定价模型能客观反映金融市场中波动率的随机性,在实际金融交易市场中的实用价值很大。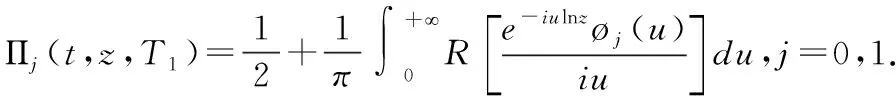




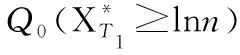
结语

